There are certainly distinct allocation strategies depending on the assumed dynamics of risky asset prices. T here was no clear pattern of structural increase in volatility on the Moroccan equity market, except for the appearance of significant instantaneous peaks. It is the consequence, more than the cause, of the instability of the Moroccan stock market. The development of arbitrage between investment instruments increases overall liquidity thus reducing volatility.

Keywords: volatility, GARCH, return, MASI index, empirical volatility

In the Moroccan stock market, which is illiquid, it happens that the frequency of quotations decreases and therefore the stock prices remain unchanged over a certain period. In this case, low volatility should not be interpreted as a low market risk, but as a high liquidity risk. It is therefore clear that the analysis of volatility alone does not prove a complete control over the market risk suffered by the financial players. Volatility is an approximate and biased indicator of risk, whether it is an empirical volatility calculated from past prices (historical volatility) or an implied volatility estimated from the evolution of stock prices.

Market volatility also depends on practical implementation and institutional investor attitudes towards portfolio diversification, namely the holding of a variety of assets whose returns are not closely correlated with each other. For example, by choosing fixed asset allocations at regular intervals, these investors help stabilize securities prices as they tend to reduce (increase) their asset portfolios that have recently depreciated (appreciated) considerably (Figure 1).

In addition, institutional investors could theoretically influence markets by moving asset prices away from fundamentals, exacerbating price movements and therefore volatility. This view is based on the size of institutional holdings relative to individual investors (Scharfstein and Stein) and (Bikhchandani and Sharma (2000).

The high price volatility is, therefore, due to this illiquidity, and not to a change in the fundamental value of the shares. In other words, the liquidity factor can be fundamental in interpreting volatility.

Financial series generally present several aspects that characterize the stochastic process associated with stock prices.

Exploratory analysis of the data

The time series data used to model the volatility of the Casablanca Stock Exchange is the daily closing price of the MASI Index. The daily profitability of MASI was calculated from its performance ¹ which is the first difference in logarithm of the closing price of the index of two successive days:

$r_t=\text{log}\left(\frac{I_t}{I_{t-1}}\right)$

Where I _{t -1} and I_t and are, respectively, the closing index of the MASI of the current day and the previous day.

Before using the MASI Index series and its performance series, one must explore the characteristics that condition the validity and reliability of their interpretations.

The stochastic processes associated with asset prices are generally non-stationary in the sense of second-order stationarity, while the processes associated with returns are consistent with the second-order stationarity property. This characteristic is the central property of ARCH processes:² they possess the properties of a homoscedastic white noise (Figure 2), but their conditional variance depends on time.

Clusters³ Volatility: It is empirically observed that large changes in yields are generally followed by small variations. There is thus a grouping of cluster extremes or volatility packages. Under these conditions, the process is conditionally heteroscedastic.

Stationarity study of the Rendement-MASI series

Unit root test (Unit Root Test) can detect the existence of non-stationarity and determine its type (TS or DS process) and are considered the best indication for stationarizing a series (Figure 3).

The idea of ​​a unit root test (Dickey Fuller) is to estimate the regression ${\text{r}}_{\text{t}}=\varphi *{\text{r}}_{\text{t}-1}+{\text{a}}_{\text{t}}$ and then ${\text{H}}_0:{\varphi }_1= 1$ test using the Student's statistic.

If we note  the null hypothesis of non-stationarity, then:${\text{H}}_0:{\varphi }_1= 1$ . rejects H_0 if ADF ADF <t-statistic t-statistic tabulated.

The hypothesis of the non-stationarity of the series of returns of the MASI index is rejected. The RMASI series is stationary⁴ and is therefore predictable.

In summary, the MASI series checks all the properties of the financial series. We can move to ARMA modeling of the RMASI yield series. Similarly, volatility evolves over time, suggesting that an ARCH process could be adapted to modeling the RMASI series.

Estimation of volatility by ARCH models

Previous Exploratory Analysis Rationale for Using Family Models ARCH to estimate volatility. Nevertheless, one can make sure of this justification by using the ARCH test applied to the residues.

The definition of an ARCH process involves the notion of conditional variance. We have seen that the conditional variance makes it possible to model the local variance of the process at each instant t, according to previous observations.

This notion can be extended at any time in the time series. Thus, the conditional expectation of the process {Xt} at time t is the expected mean value of the process at time t calculated taking into account the values of the process observed in the past. To illustrate this concept, consider the random walk (Table 1).

p = 0.0098 which we reject the null hypothesis (There is no ARCH effect) and we accept the alternative hypothesis. Volatility can be estimated by the ARCH model.

We will develop an ARCH, GARCH, EGARCH and PGARCH modeling. Then we will compare these models to retain the most appropriate data used. The decision rule used will be the AIC and SIC criteria (lowest).

This family of models is widely used in both practice and academic discourse. The model is very useful for modeling the behavior of the conditional variance of the random term of an econometric equation over time and for capturing the effect of volatility on stock prices. This model captures the dynamic characteristics of volatility according to the equation (Table 2):

${\sigma }_t^2 = \gamma V_L + \alpha * r_{t-1}^2 \beta * {\sigma }_{t-1}^2$

After estimating all these models and testing for heteroscedasticity and the autocorrelation of the residues we retain the PGARCH.

There is a growing volatility of the MASI index which becomes significant from 2007, while yields of the index turned negative. This situation obviously diverts institutional investors from equity investments (Table 3).

The fall in stock prices since the crisis therefore accentuates the decorrelation between prices and fundamentals, which is reflected in the evolution of the MASI index and the PERs of listed companies. Gains posted on the tailings corrélogrammme (in annexes) show I l ny no car horn relationship between residues. This result improves the validity of the estimated PGARCH model.

Note that P = 0.4628 <5%, so we can conclude that there is no ARCH effect in the residuals of the estimated PGARCH model.

Indeed, the AR (1) process is a Gaussian process: the tails of distribution are less thick than the tails observed on the variance of the MASI index and we do not observe a period of high volatility. ARCH models (simulated below) allow them to better take into account this kind of behavior (Table 4).

The tails of distribution can be thicker than that of the normal laws (kurtosis with the chosen parameters), and one observes, as on the empirical data, zones of strong variability (volatility).

The distinguished characteristics of this model are not only that the conditional variance is a function of time but also it is the particular form is specified. Episodes of volatility are usually characterized as shocks for the dependent variance. In the regression model, a severe shock is presented by a large standard deviation. In ARCH models, the variance of the current error, conditional on the realized error, is an increasing function of the magnitude of the delayed errors regardless of their sign. p determines the length of time with which shocks persist to cause the variance of errors to be conditioned. Finally, from the normality test, (p = 0.884417), we can say that the residues are normally distributed (Figure 4).

The appreciation of the volatility of the Moroccan stock market allows through this modeling defining the pace of its evolution and its prediction. The issue of liquidity in the equity compartment of the stock market is closely linked to the problem of volatility, which is synonymous with risk. It is a decision indicator for institutional investors who, based on their estimate, reallocate their portfolios. The volatility of the Casablanca Stock Exchange remains low in comparison with other stock markets of emerging countries or similar economies. Indeed, it was around 12% on average of ten years, while it exceeded 29% in Turkey and 16% in South Africa.

Author Calculations

Figure 1 Evolution of the Liquidity Ratio and the volatility of MASI 2004-2014

Figure 2 Evolution of the series of MASI returns between 2004 and 2014.

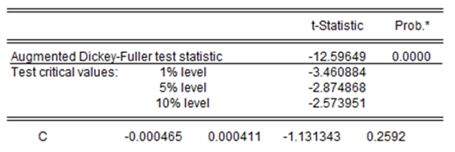
Figure 3 Augmented test Dickey -Fuller for the RMASI series.

We reject ${\text{H}}_0:{\varphi }_1=1$  because -12.59 <-2.87 and we accept ${\text{H}}_0:\text{c} = 0$  because -1.13 <2.53

Figure 4 Normality of PGARCH model residues

At¹ first sight, we find that the MASI series verifies some properties of the financial series. The pure MASI series is non-stationary, while the series of returns seems stationary.

²The studied variable should be stationary before estimating the GARCH model.

³Visually, it can be noted that periods of high volatility are followed by periods of turbulence characterized also by high volatility. Similarly, periods of moderate volatility are followed by less turbulent periods.

⁴This hypothesis tends to be difficult to verify for small samples.

⁵GARCH = C(2) + C(3)*RESID(-1)^2 + C(4)*RESID(-2)^2 + C(5)*RESID(-3)^2 + C(6)*RESID(-4)^2 + C(7)*RESID(-5)^2

⁶GARCH = C(2) + C(3)*RESID(-1)^2 + C(4)*GARCH(-1)

⁷GARCH = C(2) + C(3)*RESID(-1)^2 + C(4)*RESID(-1)^2*(RESID(-1)<0) + C(5)*GARCH(-1)

⁸(GARCH)^C(6) = C(2) + C(3)*(ABS(RESID(-1)) - C(4)*RESID(-1))^C(6) + C(5)*@SQRT(GARCH(-1))^C(6)

The sustained volatility of the Moroccan stock market confirms the underweighting of the equity portfolio in the portfolios of institutional investors, especially for Moroccan pension funds. This indicator, which provides information on the level of risk that investors can bear compared to other investment alternatives in the capital market, shows that the arbitrage made by these fund managers is not really optimized, at least because the returns the equity markets are far superior to fixed-rate assets and the volatility they present is not excessive.

There was no clear trend in the structural increase in volatility in the Moroccan equity market, except for the appearance of large instantaneous peaks. It is the consequence, more than the cause, of the instability of the Moroccan stock market. Remember that the establishment and maintenance of a climate of trust are the best antidotes against the excessive volatility of the markets. The development of arbitrage between investment instruments increases overall liquidity thus reducing volatility.

Market volatility also depends on practical implementation and institutional investor attitudes towards portfolio diversification, namely the holding of a variety of assets whose returns are not closely correlated with each other. For example, by choosing fixed asset allocations at regular intervals, these investors help stabilize securities prices as they tend to reduce (increase) their asset portfolios that have recently depreciated (appreciated) considerably.

In addition, Schwert has developed a monthly volatility estimator that is based on robust estimation techniques proposed by Davidian and Carroll (1987). This estimator has similar properties to the autoregressive conditional heteroskedasticity (ARCH) of Engle (1982).

None.

Author declares there is no conflict of interest.

1. Bel Hadj Miled K, Darwez F. Le comportement mimétique sur le marché Financier Tunisien avant et après la révolution. International Journal Economics & Strategic Management of Business Process International Conference on Business. Economics, Marketing & Management Research (BEMM’14). 2014.
2. Davanne O. Volatilité des marchés financiers et allocation d’actifs. Revue d'économie financière. 2005.
3. El Ghini A, Saidi Y.Return and Volatility Spillovers in the Moroccan Stock Market during the Financial Crisis. MPRA Paper No. 53439. 2014.
4. Leclair A, Pardo C. La volatilité, conséquence ou cause de l’instabilité des marchés financiers?. Revue d'économie financière. 2004(74):245-252.
5. Les échos épargne et investissement. La volatilité du pétrole impacte les sociétés cotées. 2014.
6. Poon S, Rockinger M, Stathopoulos K, et al. Market Liquidity and Institutional Trading during the 2007-8 Financial Crisis. Seminar at Manchester Business School. 2011.