We present an agent simulation based concept to assess aircraft collision risk (CR) for modern instrument flight procedures, focusing on the intermediate and final approach. The aircraft’s, ATC and CNS systems’ behaviors are modelled as agents-acting stochastically by means of a Monte-Carlo simulation engine-to represent a statistically realistic environment. We first draw an overall picture of current CR estimation techniques focusing on blundering aircraft as a major hazard during approach. Then, we present the ANP-based CR calculation and the agent-based simulation of nominal trajectories in detail, covering other hazards in the process. By applying the model to various approach and traffic configurations present in the literature, we could demonstrate the potential for detailed insight into CR drivers. As a selection, we present the safety case of blundering aircraft during parallel ILS approaches according to ICAO SOIR as a ‘classic’ safety case from the literature and the safety case of turning onto the final approach track of two independent parallel runways from radar vectors as a ‘novel’ application. The results indicate that published CR ‘classic’ values are reproducible from the assumptions and that only few, well-justifiable and thus verifiable model extensions are required to successfully assess derived safety cases. As such, the presented model may revive CR considerations for modern procedure design in complex TMA environments.

Keywords: collision risk modeling, agent based modeling, independent parallel approach procedure, blundering, target level of safety

The continuously growing traffic demand^1,2,3 in civil aviation forces the ATM system to utilize existing airport infrastructure and surrounding airspace at its best. Increasing traffic volumes impose additional approach and departure capacities concentrating at the runway or runway system. These may induce higher workloads for both air traffic controllers (ATCO) and pilots as the highly efficient use of pre-set sequencing and spacing constraints becomes crucial while they are also considering environmental issues such as noise abatement. While introducing important measures to minimize aircraft emissions and maximize throughput, the current high safety standards in aviation must not be compromised, but instead, pushed further in order to compensate numerically the projected traffic growth. The performance-based navigation concept,⁴ which is based on the RNP/RNAV philosophy, is a promising innovation. The European SESAR2020 project PJ01 03 focuses particularly on dynamic and enhanced routes and airspace by, for example, investigating PBN for parallel approaches. PBN allows for a more flexible route design, e.g., circumnavigating densely populated or other noise-sensitive areas during intermediate and even final approach by introducing procedure legs such as “turn to fix” or “radius to fix.” Since those new procedures will have to demonstrate equivalent safety standards compared to conventional procedures, in the course of this paper, we first present these reference values through an analysis of conventional procedures and published safety cases.

Depending on the airport runway operation mode (segregated or mixed), individual requirements have been established by ICAO to assure safe operations. However, these safety measures are somehow “static” and do not foresee specific adjustments to local conditions because no explicit cause-to-risk correlations exist in current guidance material except for the final approach segment.⁵ To overcome this lack of cause-and-effect reasoning, the present project investigates pair wise aircraft collision risk modeling (CRM), also explicitly taking controllers and flight crews into account, modelled mathematically as so-called agents. The case study assumes radar vectoring towards the final ILS approach, laterally intercepting localizer (LOC) and subsequently the glide slope (G/S) until the aircraft has crossed the runway threshold. The following four sections summarize and present (in Section 4) the results of a literature review regarding current regulations and the scientific state-of-the-art knowledge in the field of assessing operational safety during independent parallel approach procedures. We make conclusions about input parameters of the model and summarize on CRM Acceptance Criteria as the output of the model. In Section 5, we specify how the fast-time model is integrated into the overall architecture and explain how the agents are modeled. In Section 6, we transfer the specification into software in order to calculate safety and capacity metrics (i.e., probability of separation infringements and the nuisance breakout rates as detailed in Section 4.D) for various scenarios depicting traffic, runway/airspace layout and agent behavior (i.e., procedures and hazards as detailed in Section 7.A). In Section 7, we discuss the model verification concept and the results gained.

Independent parallel approach, safety

The FAA began research in the field of independent approaches to parallel runways as early as the 1960s. Since then, the MITRE Corporation in particular has progressed in developing and conducting simulations aiming at reducing runway separation requirements.^6,7 Besides developing technology like high update rate radars (down to 1 Hz), the FAA also started three major research programs: The Multiple Parallel Approach Program,⁸ the Precision Runway Monitoring (PRM) Demonstration Program⁹ and the Converging Approach Standards Technical Working Group (CASTWG). For the purposes of the MPAP and CASTWG, the FAA created a fast-time model called Airspace Simulation and Analysis for TERPS (ASAT). An ASAT study is split into the two stages of real-time, human-in-the-loop and fast-time computer-only simulation. Otherwise hard-to-reach human factors (reaction times, workload, etc.) and aircraft behavior data (e.g., roll rate, climb rate, airspeed, etc.) is acquired in the first stage. This empirical data is statistically fitted and transferred into continuous probability density functions (PDF). By means of Monte-Carlo simulation, this data is recombined with additional data from technical specifications (e.g., radar errors) while a vast amount of simulation runs helps to increase statistical significance and sharpen the confidence interval.¹⁰ Along MPAP, which was started in the late 1980s,⁸ ASAT has been used to investigate simultaneous parallel approach scenarios with dual, triple and even quadruple runway configurations within the US. Rare blunder situations (see Section 4.C) were the main interest due to the great safety impact. Therefore, the blunder occurrence probability (or blunder rate) was the central hazard for collision risk with aircraft operating on the adjacent approach track and not taking any evasive actions. To efficiently collect the most relevant data focus was merely put on such blunder-evader constellations solely along the project’s real-time experiments (Figure 1).¹⁰

Intercept of the final approach

Published studies regarding the final approach segment always assume that separation requirements will be met during the intercept maneuver even though workload is considerably high and accepted as relevant during this flight segment and important changes in the aircraft guidance mode are necessary for safe operations. As the aircraft’s headings converge, violations of separation standards could (in theory) occur suddenly and without meaningful precursor events, e.g., in case of a late or incorrect turn anticipation by the flight crew or degraded/misconfigured aircraft guidance systems. The literature does, however, not yield any safety or human factor considerations concerning these potential issues.^6‒12 Therefore, we can only take note of the fact that conservative procedure design usually foresees a vertical buffer, e.g., by displaced runway thresholds, thereby safeguarding the intercept against these and any other connected issues.

The blunder hazard

In the scope of independent parallel approaches, so-called “blunder” events require special attention.⁶ A blunder describes an unexpected deviation of an aircraft from its intended flight path (e.g., the final approach track) that does not result from ubiquitous navigational errors or could otherwise be attributed to the total system error in general, but from human error or improper functionality of technical equipment. The extent of the initial deviation from the desired track forms the blunder angle. Immediately after detection of such abnormal behavior, ATC will issue a correction advisory to the crew. In case of a non-responsive evasive aircraft, this one is called a worst-case blunder. Any potentially threatened aircraft on the adjacent approach track will receive a breakout command to relax the situation and avoid a collision (the so-called evader). By searching the FAA’s Aviation System Performance Metrics database and reviewing nearly 1,000,000 approach reports from 2008 to 2010, the authors Massimini et al.,¹³ determined a blunder rate of 1/24,000 with a blunder angle not exceeding 29° and no occurrence of a single worst-case-blunder diverting by an angle of 30° or more.

As a blunder risk mitigation measure, ICAO calls for a 2,000 ft wide No Transgression Zone (NTZ, Figure 2) placed equidistantly between the two final approach tracks, starting laterally at the distance outbound where vertical separation is first lost and extending towards the first (if staggered) runway threshold. The remaining lateral space to each runway is called Normal Operating Zone (NOZ), starting longitudinally at the localizer intercept, extending towards the individual runway threshold. Consequently, the NOZ has no pre-defined width but depends entirely on the runway spacing while considering the pre-set NTZ width. This is not at all compliant to modern concepts (e.g., the PBN philosophy⁴), indicating a necessity for further research. The NTZ dimensions are the result of a geometric construction of the flight paths of a worst-case blunder and an adjacently operating aircraft executing an evasive maneuver, which effectively dictate the minimum distance at the closest point of approach (CPA) for an aircraft pair. The case of dual blunders lies outside of this rationale and is therefore not part of this construction but rather a very rare though potentially risk-intensive corner-case.

Acceptance criteria

Obviously, safety acceptance especially of TMA procedures competes with both acceptable system capacity and also with emission abatement. Consequently, the relationship between a given CR and its implication on runway throughput is crucial for both the regulator and the operator. Therefore, we define different measures that allow an assessment of safety versus capacity.

Safety

In case of a blunder event, the risk of a collision is deter-mined by calculating the probability of two aircraft coming into physical contact. In general, this is the case if the slant range between the aircraft falls below a threshold defined by the aircraft’s physical dimensions. This “conflict risk” approach was generalized and adopted by FAA/MITRE and subsequently ICAO, and is defined as a threshold of 500ft as the ‘hit’ distance regardless of the orientation in 3D space. In ICAO’s and–built on it–SESAR’s safety regulation, the Target Level of Safety (TLS) concept, aims at defining, by means of mathematical proof, a Maximum Tolerable Frequency of Occurrence (MTFoO) for hazardous events concentrating on, but not being limited to, the ‘fatal accident’ category induced by a physical contact according ICAO Annex 13.¹⁴ For independent parallel approaches, regulation requires less than 1 violation of the 500 ft. slant-range criterion in 56 million approaches, equaling a Near Mid-Air Collision (NMAC) rate of 1.8∙10^-8 per approach.¹⁵

Assuming a final approach segment length of 10 NM and an average final approach speed of 150 KIAS, the time per final approach is approx. 4 minutes, resulting in a “conflict” frequency of 2.7∙10^-7 per flight hour. That NMAC may remain an incident but it might recur in different conditions and become an accident, depending on the moderating events and conditions. The ICAO TLS for fatal obstacle collision accidents during ILS final approaches is 1∙10^-7 per approach.⁵ A study from MITRE however proposes a much stricter target for NMAC rate in close-to-terrain operations, with a value as low as 1∙10^-9 per approach even though a non-catastrophic consequence is associated to that hazard, argued with the fact that escape procedures are physically constrained downwards.¹⁶ It is therefore important to stress that this value does not equal an accident-type TLS; historical incident data proves that only a small portion of slant-range violations indeed led to an accident, whereas the majority fell into the severe incident category according ICAO Annex 13.¹⁴ Therefore, it is necessary to consult recent safety publications such as SESAR¹⁷ for comparison and interpretation.

Capacity

During parallel approaches, a blunder should induce a breakout maneuver of an aircraft operating on the adjacent approach track, this one then following the published missed approach procedure. This scheme enforces safety at a minimal cost of capacity. Since aircraft are subjected to navigational tolerances, NTZ alerts may be triggered by aircraft deviating from but autonomously returning to their approach track. Nevertheless, the (automatically triggered) NTZ alert requires ATC to ‘break’ the adjacent aircraft ‘out’ of the approach. This is called a nuisance breakout in the sense of a false positive alert (see scenario A in (Figure 2). The frequency of such events is called nuisance breakout rate (NBR) and forms a (lost) capacity measure. Fixing a general NBR target is however unrealistic since it depends on many factors, e.g., on the traffic mix and the given runway spacing. To give indications about NBR estimates, we find in Massimini⁷ that the NBR estimated is considerably below 5% of all approaches. In Mc Cartor & Ladecky,¹² aircraft performing an RNP 0.3 (non-precision) approach are observed to cause similar nuisance breakouts 2-4% of the time.

Figure 1 Schematic runway configuration and approach layout as it is considered in the CRM application.

Figure 2 Scenarios related to Blunder. A: nuisance breakout. B: blunder recovering after ATCO intervention. C: worst-case blunder, not reacting on ATCO commands. D: double blunder (all not to scale).

Overview

The configuration of our integrated agent-based traffic simulation and collision risk estimation model, which studies though is not limited to the safety case of independent parallel approach operations (Figure 3), comprises multiple interacting modules that are triggered repeatedly following a Monte-Carlo parameter variation scheme. Previous work in development and application of the model is described in.^18‒22 For the safety case focused on in this paper, the following CRM parts were customized: the independent parallel approach configuration including all associated parameters (green colors in Figure 3), the definition and calculation of relevant metrics (blue) and customizations to the visualization. After a short introduction to the core model (traffic simulation, collision risk quantification, parameter variation, orange), these customizations are covered in detail, followed by geometric construction of the infrastructure and scenario definition descriptions.

CRM-agent based traffic simulation

The main idea of an agent-based model is creating software entities, which closely resemble real-world entities in terms of knowledge (information base), behavior (rules of deciding and acting) and communication (sensing the environment, interacting with other agents) without ‘cheating’ for the sake of efficient modeling or computing. The main benefit is emergent behavior, where a multiplicity of well-modeled software agents exhibit the same features as their real-world counterparts without the need for explicit modeling of complex traits.¹ Although getting the behavior ‘right’ is often troublesome, the major benefit is that the model is generative, meaning it is able to predict patterns outside the evident behavior specification which can be (and often are) ‘wrong’ but which may provide valuable insight into unforeseeable hazards; this is particularly relevant in the aviation domain. Except for the aircraft and flight guidance agents, all other work is purely event-driven (e.g., radar pattern detected, reaction/reading time passed). The emergent behavior is the timed sequence of events shaping the synchronous aircraft movements, whereby the concept explicitly addresses the missing cause-to-effect relations as elaborated in Section 3 (Table 1).

Agent action sequence for the blunder event

The agent logic is best understood following an assumed blunder-evader constellation as depicted in Figure 2. Agent entities will be underlined in this sub-section. Initially, both aircraft are following their specific approach track. Upon blunder initiation, the blundering aircraft’s flight guidance reverts to vectoring mode with a new heading given by the blunder angle and the initial approach track. It is reached by modeling a constant bank rate of  by the autopilot either until reaching the bank limitation ⁵ (for clean configuration) or the standard procedure turn rate of . The final turn radius and the required bank for a procedure turn observing the bank limitation are calculated as follows:

$r=\frac{{\upsilon }^2}{g\cdot \tan \Phi }$    (1)

$\Phi =\min \left(a\tan \left(\frac{\upsilon \cdot \dot{\Psi }}{g}\right),25°\right)$    (2)

During the period of ‘rolling up,’ the aircraft will follow an EULER spiral (clothoid). The on-following curve with constant bank and speed is circular. It is correctly terminated by the autopilot with the appropriate ramp-down of the roll, resulting in a clothoid transition towards the anticipated blunder heading. While performing the described maneuver, the blunder position is radar-detected and passed on to the controller, upholding all performance assumptions (e.g., delay, resolution). Upon such ‘evident’ NTZ penetration, the according software module inside thecontroller agent will trigger the ‘alert.’ The behavior is pre-defined: break out of the (previously paired) aircraft on the adjacent approach track again by means of vectoring, optionally adding a vertical guidance and requesting the blunder aircraft to immediately return to its initial approach track. For the ‘classic’ ICAO SOIR blunder scenario, all reaction and communication times are subsumed by ICAO’s original assumption of statically 8s.¹⁵ This incorporates the controller’s reaction time to the NTZ alert, voice-com and the pilot’s reaction time until aircraft compliance with the advisory. Following ICAO’s assumptions, we only assume 8s total reaction time from NTZ alert to aircraft reaction and procedure turns (i.e., no manual aircraft handling assumed). It is obvious, that this static assumption does not correctly reflect a human-machine-system, which is always stochastic. The fixed value was chosen as an initial baseline for validation reasons.

To minimize time-based discretization effects induced by the Monte Carlo simulation engine, blunder events are also synchronized with the chosen simulation update period (e.g. 0.5s). When initiating the evasive maneuver, small corrections (<1 update cycle) are applied to compensate time-discretization errors (radar, controller reaction). By the more sophisticated design of our simulation system mostly overridden for this study, the controller reaction time would be built from a blocking resource model resembling the top-level task items of scanning the radar screen, conflict inspection, decision-making²³ and advisory transmission (including interruptible read-back and compliance monitoring). The advisory transmission would require a free voice-com channel and the utterance would be accounted for according to ACT-R²⁴ with syllable and word pause times, etc. Finally, the pilot reaction time will be modeled with a PDF evaluated in a previous human-in-the-loop study.²²

Using knowledge about human factors, the total reaction time could be estimated as:

1. Controller reaction.
2. Voice-com on free channel.
3. Pilot reaction.
4. Pilot input to the aircraft.

Let (1) be almost immediate due to uniqueness of the alert and the pre-defined actions, except for the necessity to look up the evader call sign at the radar screen (GOMS complex information look-up, 1200 ms).²⁵ (2) can be calculated by the syllable/word count of the advisory according to ICAO phraseology and phonetics and metrics from ACT-R,²⁴ e.g. air-line_1_2_3_turn_left_hea-ding_4_5_6_im-me-diate.

15 syllables+10 word gaps+initiation+comprehension

15*50ms+10*100ms+150ms+180ms=2,080ms

With 1,540ms and 0 to 2,000ms on average (depending on the input strategy), (3) and (4) can be adopted from Vogel et al.,²² where a pure human factors estimate is presented as well. In total, we can account for 5 to 7 s (4,820 to 6,820 ms on average) of the 8 s assumption without taking the radar update rate into account; this then appears roughly valid considering that much time can be saved by observing the controller’s acute voicing in hazardous situations and early cue words in ICAO phraseology. Once configured by the pilot, the evader autopilot will initiate the same aircraft turn maneuver as described in the beginning of this sub-section. In parallel, a second controller who simultaneously monitors the blunder’s approach track will initiate a comparable advisory to the blundering aircraft, whose pilot would subsequently start implementing the corrective maneuver (‘normal’ blunder) or fail to react (‘worst case’ blunder).

Aircraft navigation performance

With respect to the defined navigation aids, all trajectories produced by the traffic simulation are ideal and incorporate all of the features of the agents’ decision-making including timing, which we call microscopic because of the fine-grained dependencies between agents (e.g., milliseconds of reaction time deciding upon which aircraft is being served first by ATC). In addition, all flight movements are known to exhibit a navigational error consisting of path definition, navigation system and flight technical errors. We handle these errors on a macroscopic level. By analyzing large radar data sets and filtering flights navigating autonomously only on flight guidance systems (no manual control, no active ATC advisories), and statistically fitting (often heavily tailed) PDF, all micro-effects stemming from weather (e.g., turbulent wind), control system dynamics, etc. can be summed up into one distribution (independently per axis of the trajectory-fixed coordinate system; i.e., cross-track, along-track, vertical-track tolerance, XTT, ATT, VTT). We refer to these PDF of navigational accuracy as actual navigation performance (ANP) equivalent, but not limited to, the term used in PBN.^26,27

Monte-Carlo evaluation and numeric complexity

We utilize pseudo-random variables in order to efficiently and reproducibly assess the influence of arbitrarily distributed stochastic parameters present in the form of aircraft pairing, navigation tolerances (ANP), radar accuracy and reaction times. Normally, to determine a risk of less than 10^-8 collisions per approach (due to blundering) with an accuracy of 5%, the simulation needs to span far more than 10 quadrillion approaches according to the Bernoulli Law of Large Numbers, as quantified by Chebyshev ‘s inequality in (3). Here, the simulation is considered a Bernoulli experiment (collision yes/no) which is repeated  times, in which a collision is recorded times. The type-I error probability is set to 1-P=0.05 and the probability estimation tolerance is set to per aircraft pairing. These values represent a general engineering confidence interval, which certainly may be debatable for life critical applications.

$P\left(\left|\frac{n_1}{n}-p\right|<\epsilon \right)\ge 1-\frac{1}{4{\epsilon }^{2}n}$

$\frac{1}{4{\left({10}^{-8}\right)}^{2}n}\ge 0.05$   (3)

$n\ge 5\cdot {10}^{16}$

The computational effort can, however, be reduced by focusing on approach “points of interest:” Assuming a blunder rate of 1/24,000 leads to 500 billion approaches to simulate. In contrast to this theoretic approximation, FAA conducted studies where a similar simulation was run 100,000 times.⁹

¹ Ant colonies on their quest for food, based only on the description of one archetypical ant are a classic early example of agent-based models.

Figure 3 Agent based model architecture with monto-carlo simulation capability.

Definition of metrics

First, we defined the assessment metrics, which we call acceptance criteria. For each such criterion, tool users have to define acceptance thresholds for the given ATM procedure design with regard to safety (collision probability) and capacity (aircraft throughput). According to historical models and studies, we adopt the concept of the number of Test Criteria Violations (TCV) to define a safety metric as outlined in Section 4.D, targeting severe incidents instead of a pure collision risk (CR). The latter can, however, be estimated by reducing the ‘hit’ distance to the aircraft’s physical dimensions. The slant range between blunder-evader aircraft pairs is therefore continuously traced. If it falls below a given threshold, a TCV is recorded. Finally, the probability of a TCV based on its number of occurrence and the total number of simulated events is calculated as follows:

$P\left(TCV\right)=\frac{N_{TCV}}{2.N_{Events}}\cdot P(Blunder)$   (4)

The widely accepted assumption of a fixed blunder probability $P_{Blunder}$ helps to increase computational efficiency. The blunder-evader results are collated with inherently safe normal operations as a post-processing step. The NBR is also calculated analytically during post-processing using the NTZ penetration probability and the physical runway layout. Both approach tracks’ NBR are calculated separately by integrating geometrically the cross-track ANP distribution function along the extended runway centerline, as shown in (5). Figure 4 illustrates this process. Yellow-grey areas under the Normal Distribution function depict NTZ penetration probabilities at single points as the integral of the cross-track deviation. The length of the final approach track along the NTZ boundary is denoted as . The overall NBR is the counter-probability of the event that “on neither approach track, a nuisance breakout occurs.” All NBR values depend on the current navigation accuracy.

$P_{NTZ}=1-{\displaystyle \prod _0^l{\left(1-p_{NTZ}(x)\right)}^{dx}}$

$$=1-\exp \left({\displaystyle \underset{0}{\overset{l}{\int }}\ln \left(1-p_{NTZ}(x)\right)dx}\right)$$   (5)

$P_{NB}=1-(1-P_{{}_{NTZ,left}})\cdot (1-P_{NTZ,right})$ (6)

Geometric design, stochastic variables

For the targeted safety case, airport, final approach configuration and runways are assumed to operate in single mode (approaches only) with guidance and surveillance equipment compliant to ICAO SOIR Mode 1 specifications.¹⁵ A standard ILS final approach begins with intercepting the LOC. Then, a straight horizontal flight segment is followed for at least 2NM, allowing the aircraft to establish and stabilize laterally before vertically intercepting the G/S and start to further descent until touchdown. Aircraft approaching the same or the adjacent runway must maintain radar separation (3NM laterally or 1,000 ft vertically) at all times even though they are considered ‘independent.’ The angle between intercept vector and final approach course must not exceed 30°.¹⁵ The model, however, allows for certain violations, thus reflecting navigational, control and human error. The actual LOC intercept point is subject to uncertainties (aircraft/pilot behavior) and variability’s resulting from sequencing in a vectoring onto ILS environment. These, however, are not reported in the paper and will be modeled by an appropriate PDF.

Surveillance system requirements depend on the actual runway spacing: Between 3,400ft and 4,300ft (centerline to centerline), ICAO requires a radar update rate of every 2.5 seconds. The azimuthal accuracy of the recorded aircraft positions shall match a Normal Distribution with . Beyond 4,300ft runway spacing, an update rate of only 5 seconds as well as an azimuthal accuracy of is required. Aircraft speeds are also stochastically modeled. While historical investigations by ICAO assume an unrealistic constant speed of 150 KIAS, our model is able to handle various distributions. Besides a static value, aircraft speeds may also be subjected to a Normal Distribution or following the ICAO approach category scheme.⁵ Finally, blunder parameters are stochastic variables as well. Those are the distribution of blunder occurrence along the approach track, the blunder angle and the worst-case blunder rate.

Implementation of the turn-onto-final safety case

For each simulation run, blunder-evader pairs are positioned on the parallel approach tracks. First, the distance from threshold for the blundering aircraft is chosen randomly. Subsequently, based on the provided ANP function, cross- and vertical-track deviations are determined, assuring the necessary initial adherence to the NOZ before the actual blunder event. Additional stochastic parameters are speed, blunder angle and vertical blunder behavior (leveling-off due to lost G/S signal versus upholding the current rate of descent). Now, a deterministic blunder trajectory is generated. The crossing point with the adjacent approach track is calculated and forms the mid-point of the evader placing area, which extends, plus/minus, half of the required in-trail separation, thereby covering precisely the location of the most threatened aircraft for the independent parallel approach configuration. The assigned evader placement follows a uniform distribution. Once placed, the evader is shifted back in time in order to let blunder and evader enter the simulation at the same time. After having assigned the initial positions and all aircraft parameters, the simulation continues as described in Section III.C and stops as soon as the closest point of approach (CPA) has been passed. For the minimum distance, the TCV is evaluated.

Model limitations

We currently assume that human actions are purely event driven. The controller will initiate corrective commands only after receiving a NTZ alert. The pilot agent only consecutively intervenes after receiving a command. However, in reality, the controller will most likely detect deviations during the approach well prior NTZ alert and issue appropriate commands. Additionally, pilots may also be able to detect deviations and undertake corrective maneuvers without ATCO recall. The model therefore is rather conservative, probably too deterministic at this point. Furthermore, the distribution functions used to represent navigation tolerances presume a Brownian motion, flight mechanics are widely neglected. This theoretically allows an aircraft to suddenly change attitude in space between two simulation steps. At the same time, the employed ANP functions are considered to be independent while deviations from the flight path may not. ANP functions were deduced from recorded real flight paths and are therefore environment specific. Data contains environmental effects like winds, which will often be specific for the location, and the time the data was recorded. Therefore, reference data should contain a very large range of all external effects. Alternatively, locally fitted ANP functions should be developed and human reaction times modelled stochastically. The model is technically prepared to do so. We will consider these issues in consecutive research.

Figure 4 Schematic view of the integration volume (thick grey outlines) used to compute the NBR. Distributions are exemplary cuts along the continuous approach track.

Model verification using the ‘classic’ ICAO Scenario

The fast-time model shows that results are comparable to those of previous simulation studies by ICAO. This is shown in the following, by running two exemplary use cases. While for intercept maneuvers there is no comparable study available, we configured the mode (final approach blunder, nuisance breakout and aircraft behavior modules) to be comparable with historical studies. Hence, we expect the model to remain valid and to deliver results that are directly comparable with the ‘classic’ baseline.

Many parameter settings follow directly the ICAO SOIR document:¹⁵

1. Aircraft speed: 150 knots
2. Blunder angle & rate: 30°&1/2,000
3. Worst-case blunder rate: 1/100
4. ILS Cross Track Deflection: 150 ft. at 10 NM from threshold (1-sigma)
5. Reaction and communication delay: 8s (static, for means of baseline validation to ICAO)
6. Radar azimuthal resolution (1-sigma): 0.3°&0.06° (for 4,300ft. & 3,400ft. runway spacing)
7. Radar update period: 5s & 2.5s (for 4,300ft. & 3,400ft. runway spacing)
8. Slant Range (NMAC TCV value): 500ft.
9. Width of NTZ: 2,000ft.

The following additional parameters were fixed by assumption, with supporting evidence from the literature:

1. Aligned (no staggered) thresholds/runways
2. VTT as in Anderson26
3. XTT linearly increasing with threshold distance26
4. Radar antenna located in the geometric center of all (four) runway thresholds (pure assumption)
5. Evader (& missed approach) climb gradient: 2.5%

Using these settings, multiple simulations, initialized with individual random ‘seed’ values, were conducted. Figure 5 visualizes the development of resulting probability over an increasing number of simulated blunder-evader pairings. The results stabilize at a probability of around TCV per approach, which is close to the ICAO value of  (one TCV per 56 million approaches).¹⁵ The remaining differences do result from implementation details (e.g. clothoid) and model parameterization (e.g. ILS deviations). Especially, we found high sensitivity to TCV probability towards the final approach length, which was set to 10 resp. 13.5NM for both runways to allow for immediate blundering towards NTZ. When applying 10NM for both runways, the probability drops significantly down to around TCV per approach. This ILS specific effect is subject to further research.

The turn-onto-final safety case

The ‘novel’ safety case now covers additionally the LOC intercept including the additional hazard of weak interception due to human error such as e.g., flight guidance mode-confusion. The model handles such events identically to those on final approach, with the difference that the blunder initiation is linked to the nominal intercept point and the ‘blunder’ heading is assumed to be already reached. In contrast to the ‘classic’ scenario, the NTZ, extending outwards until vertical separation is no longer granted,¹⁵ does not cover that airspace entirely. Instead, vertical separation set to 1000ft. between left and right approach safeguards the intercept procedure. Following the stated assumptions, proactive controller interventions (without NTZ alert) are not considered. This is a rather weak assumption from reality. Therefore, the current agent behavior represents a conservative (static & worst-case) safety consideration. The resulting points of closest approach (slant distance color-coded) are shown in Figure 6.

Figure 7 shown below depicts the measured aircraft slant ranges and TCV violation threshold. Although the worst-case assumptions and visual images laid out above suggest a more critical behavior than in the ‘classic’ scenario, the opposite is true: due to the 1000ft. vertical separation set out until G/S intercept, no TCV occurred over the 10 million simulated pairings. Therefore, we cannot show any stabilization of TCV rate results as part of Figure 7. To investigate further, a more critical case lowering virtually vertical separation down to 800ft was selected. Figure 8 depicts the corresponding effects: The slant range distribution is shifting towards lower values (rightwards), TCVs do occur: Its rate now stabilizes similarly to Figure 5 at a value of per approach. These kinds of procedure design studies, along with re-shaped (elongated) NTZ geometries, form potential future application of the presented model.

Discussion of runtime complexity and outlook

First, the quality of results does depend on the time discretization performed during all computer-numerical simulations. By applying corrections below one time increment (update period), we were able to compensate and stabilize the results (Figure 9). Second, the runtime requirement certainly depends on the expected probability of ‘positive’ observations (e.g., NMACs). Running multiple simulations over a wide range of blunder events shows that results stabilize at around 3 million events, as depicted in Figure 5 & Figure 8. 100,000 simulation runs as published in¹⁵ are, consequently, far too little for reliable results. Third, it is important to recall that the probability value for a TCV, as given by ICAO, does not represent an accident-type of TLS since historical incident data proves that only a small minority of slant-range violations indeed led to accidents, whereas the majority fall into the severe incident category (NMAC) of ICAO Annex 13.¹⁴ Therefore, it is necessary to consult recent safety publications such as¹⁷ for comparison and interpretation. The document offers a translation of a singular TLS value into seven incident/accident severity categories and correctly connects safety with reliability by declaring a “Maximum Tolerable Frequency of Occurrence” (MTFoO).

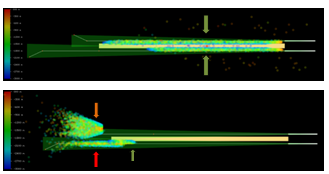
Figure 6 Visual comparison of ‘classic’ (top) vs. ‘novel’ (bottom) safety cases: Blunder events during LOC intercept are not entirely NTZ safeguarded, but 1000 ft. vertical separation is assumed (green arrows=resolved blunder events, red & orange arrows=undetected blunder events).

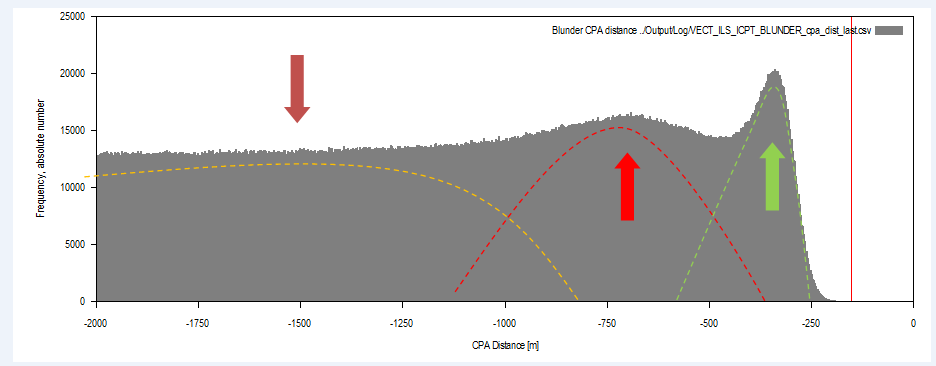
Figure 7 The ‘novel’ safety case: blunders on the final approach, density of aircraft pair slant distance with indicated TCV (red line, top) and therory of underlying distributions (colored arrows and dashed lines matching Figure 6.

Figure 8 Modified ‘novel’ safety case with reduced vertical separation (800 ft.), density of aircraft pair slant distance with indicated TCV (red line, top), development of probability over the number of simulated blunder events. (Bottom)

Figure 9 Reduced influence of time stepping (simulation update period) on resulting TCV rate, with comparison to published value in ICAO SOIR.¹⁵

The present work is conducted under a contract with the EUROCONTROL Experimental Center to develop a collision risk model in support of the safety case for the SESAR2020 project on PBN for parallel approaches (PJ01-03). The authors sincerely thank Karim Zeghal and Bruno Rabiller from Eurocontrol Experimental Center for their careful support and feedback during this project.

The author declares that there is no conflict of interest.

1. Global market forecast 2016-2035. France: Airbus; 2016. 124 p.
2. Current market outlook 2016-2035. Chicago: Boeing; 2016. 54 p.
3. 20-year Forecast of Annual Number of IFR Flights (2012-2035). Belgium: EUROCONTROL; 2013. 64 p.
4. Performance-based Navigation (PBN) Manual. Canada: International Civil Aviation Organization; 2008. 294 p.
5. Procedures for Air Navigation Services-Aircraft Operations (PANS-OPS). Canada: International Civil Aviation Organization; 2006. 279 p.
6. Haines AL, Swedisch WJ. Requirements for Independent and Dependent Parallel Instrument Approaches at Reduced Runway Separation. Virginia: Federal Aviation Administration; 1981. 185 p.
7. Massimini SV. Simultaneous Independent and Dependent Parallel Instrument Approaches. Virginia: MITRE; 2006. 27 p.
8. FAA. Terminal Air Traffic Control Radar and Display System Recommendations for Monitoring Simultaneous Instrument Approaches. Springfield: National Technical Information Service; 1999. 30 p.
9. William J Hughes. Precision Runway Monitoring Demonstration Report. Washington: PRM Program Office; 1991. 136 p.
10. EUROCONTROL/FAA. A Concept Paper for Separation Safety Modeling. 1989.
11. Magyarits SM, Ozmore RE. Evaluation of Triple Independent Instrument Landing System Approaches to Runways Spaced 4,000 Ft and 5,300 Ft Apart Using A Precision Runway Monitor System. New Jersey: Federal Aviation Administration; 2002. 61 p.
12. McCartor G, Ladecky S. Safety Study Report on Triple Simultaneous Parallel Instrument Landing System (ILS) and Area Navigation/Required Navigatio Performance (RNAV/RNP) Approaches at George Bush Intercontinental Airport (KIAH). Oklahoma: Flight systems Laboratory; 2005. 45 p.
13. Massimini SV, McNeil GC, Tene N. Frequency and severity of deviations during simultaneous independent approaches to parallel runways. Herndon: In Integrated Communications, Navigation and Surveillance Conference (ICNS); 2010. 24 p.
14. Aircraft Accident and Incident Investigation. Canada: International Civil Aviation Organization; 2001. 43 p.
15. Manual on Simultaneous Operations on Parallel or near parallel Instrument Runways (SOIR). Canada: International Civil Aviation Organization; 2004. 34 p.
16. Henry M. A Monte Carlo Simulation for Evaluating Airborne Collision Risk in Intersecting Runways. American Institute of Aeronautics and Astronautics; 2010. 21 p.  
17. Guidance to Apply the SESAR Safety Reference Material. Europe: SESAR; 2014. 335 p.
18. Vogel M, Thiel C, Fricke H. A Quantitative Safety Assessment Tool Based on Aircraft Actual Navigation Performance. Budapest: In International Conference on Research and Air Transportation (ICRAT); 2010. 8 p.
19. Vogel M, Thiel C, Fricke H. Assessing the Air Traffic Control Safety Impact of Airline Pilot induced Latencies. London: In International Conference on Application and Theory of Automation in Command and Control Systems (ATACCS); 2012. 8 p.
20. Vogel M, Thiel C, Fricke H. Simulative Assessment of Reduced Lateral Separation Minima for the Terminal Airspace. San Francisco: In International Conference on Research and Air Transportation (ICRAT); 2012.
21. Vogel M, Schelbert K, Kistan T, et al. Analysis of Airspace Complexity Factors' Capability to Predict Workload and Safety Levels in the TMA. Chicago: In Air Traffic Management Research and Development Seminar; 2013. 10 p.
22. Vogel M, Thiel C, Fricke H. Experimental Quantification of Times Needed to Comply With Air Traffic Control Advisories (FCU & MCDU Interaction). Bologna: 5th SESAR Innovation Days; 2015. 12 p.
23. Kieras D. A Guide to GOMS Model Usability Evaluation using NGOMSL: In Handbook of Human-Computer Interaction. 2nd ed. Helander MG, Landauer TK and Prabhu PV editors. North-Holland: Amsterdam; 1997. 733‒766 p.
24. Anderson JR. ACT-A simple theory of complex cognition. American Psychologist. 1996;51(4):355‒365.
25. Kieras D. A Guide to GOMS Model Usability Evaluation using GOMSL and GLEAN4. USA: University of Michigan; 2006.
26. Thiel C, Fricke H. Collision Risk on Final Approach–A Radar Data Based Evaluation Method to Assess Safety. Budapest: In International Conference on Research in Air Transportation (ICRAT); 2010. 8 p.
27. Thiel CC, Vogel M, Fricke H. Safety Monitoring of New Implemented Approach Procedures by Means of Radar Data Analysis. Berkeley: Proceedings of the 5th International Conference on Research in Air Transportation (ICRAT); 2012.
28. Vogel M, Thiel C, Fricke H. Simulation-based risk analysis of the aviation-integrated safety assessment model for approach and departure procedures in the context of the introduction of performance-based navigation. International Transportation; 2015.