The time profiles of electric conductivity for cross-linked magnetic elastomers at high electric fields were measured in the absence of magnetic fields. The magnetic elastomer is cross-linked polyurethane containing carbonyl iron particles. The electric conductivity for magnetic elastomers simply decreased with an elapse of time and took a constant value at typically ~100s after applied the electric fields. The decrease in the electric conductivity was in proportional to the volume fraction of magnetic particles, indicating that the carriers for the electric conduction are positively or negatively charged ions which were diffused from the magnetic particles. On the other hand, the electric conductivity for magnetic elastomers with a volume fraction of 0.27 decreased, however it reversed to increase at ~50s, which is an indication of the dielectric breakdown behavior. When the electric field was removed, the electric conductivity was completely recovered to the initial value within 1 min. The mechanism of electric conductivity is discussed for understanding the electric conduction and dielectric breakdown for magnetic elastomers.

Keywords: polyurethane, magnetic elastomer, electric conductivity, dielectric breakdown

Soft materials responsive to external stimuli such as temperature, pH, electric fields, have attracted considerable attention as next generation actuators, devices with virtual reality, or soft robots etc. Magnetic elastomer is a soft material responsive to magnetic fields and is consisting of polymeric matrices and magnetic particles. When magnetic fields are applied to magnetic elastomers, the viscoelasticity of the magnetic elastomer significantly increases, which is called the magneto rheological (MR) effect.^1‒5 So far, we have reported a new class of magnetic hydrogels and elastomers that exhibit drastic and reversible changes in dynamic modulus without using strong magnetic fields.^6‒9 We have also reported that bimodal magnetic elastomers consisting of magnetic and nonmagnetic particles exhibit the enhanced magneto mechanical response compared to the monomodal magnetic elastomers.^10‒13 Recently, magnetic elastomers attract much attention as damping materials which can control the resonant frequency of vibration by magnetic fields. It is because that the elastic modulus of magnetic elastomer can be changed continuously by magnetic fields. Normally, a general damper has a certain resonant frequency depending on its elastic modulus. Therefore, many dampers with some different elastic modulus are needed for absorbing vibrations with various frequencies. In aerospace, damping materials with variable resonant frequency are much useful compared to the earth because the inertial effect is very remarkable, e.g. dampers for solar panel for artificial satellite or space station. As far as we know, magnetic elastomers with variable resonant frequency have not been employed in aerospace materials so far.

As well as the rheological response by magnetic fields mentioned above, the electric conductivity for magnetic elastomers alters in response to magnetic fields. Accordingly, the elastic modulus can be sensed by the electric conductivity for magnetic elastomers. So far, many researches relating to the electric conductivity for magnetic elastomers have been reported in literatures.^14‒16 Recently, the application using the electric characteristics for magnetic elastomers to sensors is widely and acceleratingly developed, e.g. highly stretchable electrodes and stretchable lighting devices,¹⁷ the effect of pressure or strain on the electric conductivity for magnetic elastomers,¹⁸ drastic magnetic response of electric conductivity of graphite doped magneto rheological plastomers.¹⁹ In general, most of measurements of electric conductivity for magnetic elastomers is carried out by using low electric voltages, e.g. ~10V. The electric conductivity at low electric fields gives us information about the mobility of carriers which flow in the material without dielectric breakdown. On the other hand, the electric conductivity at high electric fields demonstrates the mobility of carriers which conduct chains of magnetic particles accompanying with the dielectric breakdown at the gap between the discontinuous chains. In advance to the measurement under magnetic fields, it should be cleared that the dynamic behavior of carriers under no magnetic fields when an electric field was applied. In this study, we measured the time profiles of electric conductivity for magnetic elastomers with various volume fractions of magnetic particles under various strengths of electric voltages.

Polyurethane elastomers and magnetic elastomers were synthesized by a pre-polymer method. Polypropylene glycols (Mw=2000, 3000), toluene diisocyanate, carbonyl iron (CI-SM) particles with a diameter of 2.5µm, and a plasticizer (dioctyl phthalate, DOP) were mixed by a mechanical mixer for several minutes. Polyurethane elastomers without magnetic particles were obtained by the similar procedure as magnetic elastomers without using the magnetic particle. The mixed liquid was poured in a silicon mold and cured at a hot stage for 20min at 100°C. The concentration of DOP was defined by the ratio of DOP to the matrix without magnetic particles and it was fixed at 65 wt.%; DOP/(DOP+matrix). Magnetic elastomers with volume fractions of magnetic particles ranging from 0.02 to 0.27 were prepared in this study. The electric conductivity for magnetic elastomers was measured by two terminals method using a high resistance meter (DSM-8104, HIOKI) at room temperature. The voltage was varied from 10V to 1kV. The data of electric resistance was measured at 1s after when the voltage was applied. The sample was a disk 20mm diameter and 2.0mm thickness, and it was sandwiched between the electrodes made of cupper-beryllium alloy. The measurement was performed for three samples obtained from different batches.

Figure 1A shows the time profiles of electric conductivity at 500V for magnetic elastomers with various volume fractions of magnetic particles. The electric conductivity for polyurethane elastomers without magnetic particles slightly decreased with an elapse of time. The electric conductivity took a constant value after approximately 40s. As increasing the volume fraction of magnetic particles, the electric conductivity largely decreased with an elapse of time. The time for reaching the equilibrium was longer (~100s) with increasing the volume fraction of magnetic particles. Therefore, the decrease in the electric conductivity is caused by the decrease in the mobile ions in magnetic elastomer due to the electrode polarization effect. It is well known that the electric conductivity strongly depends on the compression strain applied by electrodes, i.e. the electric conductivity increases with the strain, especially in the presence of magnetic fields. In the present study, the compression strain was kept at 0.01 for all measurements; therefore the compression effect can be neglected.

Figure 1B shows the time dependence of the electric conductivity at 1000V for magnetic elastomers with various volume fractions of magnetic particles. As well as the conductivity at 500V, both the electric conductivity for polyurethane elastomers slightly decreased with an elapse of time. Magnetic elastomers demonstrated that the electric conductivity largely decreased with the time. The electric conductivity for polyurethane elastomers took a constant value after approximately 40s, and it for magnetic elastomers without a volume fraction of 0.27 was approximately 150s. For magnetic elastomers with a volume fraction of 0.27, the electric conductivity suddenly decreased when the electric field was applied, however it turned to increase at approximately 10s. The lag time can be considered as an induction time for the dielectric breakdown. The dielectric breakdown accompanying with a lag time might be caused by a secondary effect such as local heating which is taken place at the gap between magnetic particles. After the electrode polarization, the electric field is considered to be concentrated at the gap between particles; this might lead the local heating.

Figure 2 depicts the relationship between the electric conductivity at 500V and the volume fraction of magnetic particles for magnetic elastomers. The electric conductivity at 0s, σ₀, for magnetic elastomers linearly increased with the volume fraction of magnetic particles. This strongly indicates that magnetic particles contain conductive carriers which are diffused by an application of electric voltages.²⁰ On the other, the electric conductivity at 300s, σ_∞, for magnetic elastomers was independent of the volume fraction of magnetic particles. This suggests that the conductive carriers were completely polarized by the electric field at 300s.

Figure 3 indicates the relationship between the decrease in the electric conductivity σ₀-σ_∞ and the volume fraction of magnetic particles at various voltages. It was found that the decrease in the electric conductivity increased in proportional to the volume fraction of magnetic particles at all voltages. This evidence shows that the electric conductivity occurs by conductive carriers leaked from magnetic particles. The value of the slope increased with the applied voltage below 100V and it was constant at high voltages, indicating that the applied voltage is high enough to drag out conductive ions from magnetic particles.

Figure 4A demonstrates the recovery in the electric conductivity for polyurethane elastomers without magnetic particles. The electric field was cut at 300 s and was applied again to the elastomer after an interval of 60s. At both electric voltages, the electric conductivity recovered to high values compared to the last value at 300s although the difference was extremely small; 1.3% and 1.7% higher than the last values for 30V and 500V, respectively. Figure 4B shows the recovery in the electric conductivity for magnetic elastomers with a volume fraction of 0.27. At both electric voltages, the electric conductivity clearly recovered to the original values indicating that the polarized ions randomly distributed in magnetic elastomers by thermal agitation as schematically illustrated in Figure 5

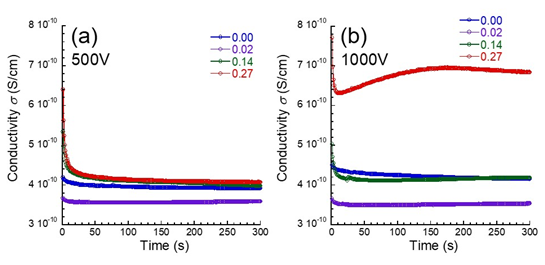
Figure 1 Time profiles of electric conductivity at (A) 500 V and (B) 1000 V for magnetic elastomers with various volume fractions of magnetic particles.

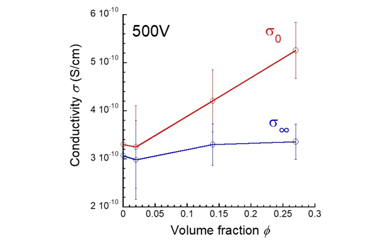
Figure 2 Electric conductivity at 0 and 300s for magnetic elastomers measured at 500V as a function of the volume fractions of magnetic particles.

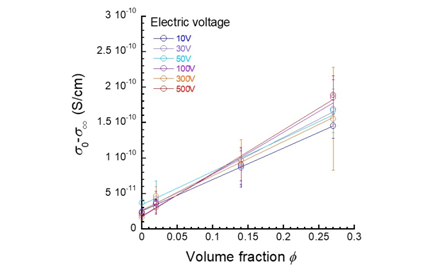
Figure 3 Relationship between the decrease in electric conductivity σ0-σ∞ and the volume fractions of magnetic particles at various electric voltages.

Figure 4 Recovery in the electrode polarization at 30 and 500V for (A) polyurethane elastomers and (B) magnetic elastomers with a volume fraction of magnetic particles of 0.27. The electric field was cut at 300s and applied again at 360s.

Figure 5 Possible explanation for time-dependent electric conductivity for magnetic elastomers containing carbonyl iron particles.

We investigated the time profiles of the electric conductivity for magnetic elastomers containing magnetic particles with various volume fractions and at various electric voltages. Typically, the electric conductivity for magnetic elastomers exhibited a time-dependent behavior; it decreased with an elapse of time and took a constant value at approximately 100s after applying electric voltages, which is due to the electrode polarization of conductive carriers diffused out from magnetic particles. Magnetic elastomers with a volume fraction of 0.27 showed the dielectric breakdown behavior at 1000V with showing a lag time, which might be caused by a secondary effect such as local heating between magnetic particles. The electric conductivity recovered to the original value within 60s after cutting off the electric voltages indicating that the carriers relax to the random distribution by thermal agitation. These results presented here would be useful for understanding the conduction mechanism or the dielectric breakdown occurred in magnetic elastomers.

This research was partially supported by TAKEUCHI Scholarship Foundation (No. 160005) and The UNION TOOL Foundation.

The authors declare no conflict of interests.

1. Xu YG, Gong XL, Xuan SH. Soft magneto rheological polymer gels with controllable rheological properties. Smart Mater Struct. 2013;22(7):075029.
2. Gong XL, Xu YG, Xuan SH, et al. The investigation on the nonlinearity of plasticine-like magnetorheological material under oscillatory shear rheometry. Journal of Rheology. 2012;56(6):1375.
3. Xu YG, Gong XL, Xuan SH, et al. Creep and recovery behaviors of magnetorheological plastomer and its magnetic-dependent properties. Soft Matter. 2012;8:8483‒8492.
4. Sun TL, Gong XL, Jiang WQ, et al. Study on the damping properties of magnetorheological elastomers based on cis-polybutadiene rubber. Polymer Testing. 2008;27(4):520‒526.
5. Chertovich AV, Stepanov GV, Kramarenko EYu, et al. New Composite Elastomers with Giant Magnetic Response. Macromolecular Materials and Engineering. 2010;295(4):336‒341.
6. Mitsumata T, Abe N. Magnetic-field Sensitive Gels with Wide Modulation of Dynamic Modulus. Chemistry Letters. 2009;38(9):922‒923.
7. Mitsumata T, Honda A, Kanazawa H, et al. Magnetically tunable elasticity for magnetic hydrogels consisting of carrageenan and carbonyl iron particles. J Phys Chem B. 2012;116(40):12341‒12348.
8. Mitsumata T, Ohori S, Honda A, et al. Magnetism and viscoelasticity of magnetic elastomers with wide range modulation of dynamic modulus. Soft Matter. 2013;9:904‒912.
9. Mitsumata T, Ohori S. Magnetic polyurethane elastomers with wide range modulation of elasticity. Polymer Chemistry. 2011;2:1063‒1067.
10. Ohori S, Fujisawa K, Kawai M, et al. Magnetoelastic Behavior of Bimodal Magnetic Hydrogels Using Nonmagnetic Particles. Chemistry Letters. 2013;42(1):50‒51.
11. Mitsumata T, Ohori S, Chiba N, et al. Enhancement of magnetoelastic behavior of bimodal magnetic elastomers by stress transfer via nonmagnetic particles. Soft Matter. 2013;9:10108‒10116.
12. Nagashima K, Kanauchi S, Kawai M, et al. Nonmagnetic particles enhance magnetoelastic response of magnetic elastomers. Journal of Applied Physics. 2015;118(2):024903.
13. Nanpo J, Nagashima K, Umehara Y, et al. Magnetic-Field Sensitivity of Storage Modulus for Bimodal Magnetic Elastomers. J Physic Chem B. 2016;120(50):12993‒13000.
14. Kchit N, Bossis G. Electrical resistivity mechanism in magnetorheological elastomer. J Phys D: Appl Phys. 2009;42(10):105505.
15. Martin JE, Anderson RA, Odinek J, et al. Controlling percolation in field-structured particle composites:Observations of giant thermoresistance, piezoresistance, and chemiresistance. Phys Rev B. 2003;67(9):094207.
16. Yu M, Ju BX, Fu J, et al. Magnetoresistance Characteristics of Magnetorheological Gel under a Magnetic Field. Ind Eng Chem Res. 2014;53(12):4704‒4710.
17. Kim S, Byun J, Choi S, et al. Negatively Strain-Dependent Electrical Resistance of Magnetically Arranged Nickel Composites: Application to Highly Stretchable Electrodes and Stretchable Lighting Devices. Adv Mater. 2014;26(19):3094‒3099.
18. Bica I, Anitas EM, Bunoiu M, et al. Hybrid magnetorheological elastomer: Influence of magnetic field and compression pressure on its electrical conductivity. Journal of Industrial and Engineering Chemistry. 2014;20(6):3994‒3999.
19. Pang H, Xuan S, Liu T, et al. Magnetic field dependent electro-conductivity of the graphite doped magneto rheological plastomers. Soft Matter. 2015;11:6893‒6902.
20. Gagan K, Raju A, Peter C, et al. Electrically conductive polymers and composites for biomedical applications. RSC Adv. 2015;5:37553‒37567