For liquid metal calculation method is studied depending on the geometric and operating parameters as averaging the heat transfer in turbulent convective heat transfer in a tube with a sequence of periodic protrusions semicircular geometry based on a numerical solution of the Reynolds equation, closable by means of shear stress transference model Menter and the energy equation for multiscale intersecting structured grids. The novelty of the calculated data on heat transfer is that they are valid for small Prandtl numbers, while the earlier similar results were obtained only for medium and large Prandtl numbers. General Analysis calculated data obtained showed that relatively high turbulators (d/D=0,90) c small pitch (t/D=0, 25) at small Reynolds number (Re=10⁴) reduction of heat transfer enhancement for the liquid metal with respect to the gas may reach more than one third other conditions being equal; increase above parameters generally leads to a decrease differences between the levels of enhancement of heat transfer between the gas and liquid metal.

Keywords: modeling, numerical, channel, trumpet, convective, menter model, the vortex generator, heat exchange, prandtl number, liquid metal

Hanesenie periodic protrusions on the wall surfaces is washed well tested in practice, the heat transfer intensification method vortex.^1,2 Intensification of heat transfer for flow conditions coolants in the tubes with turbulators held and carried mainly by experimental methods^1,2 and theoretical studies rather scarce, many of them are based on integral approaches.^3-7 At the present stage of research tasks aerodynamics and thermo vouchers and eddy currents are increasingly hesitant multiblock methods of computing technologies based on intersecting structured grids.^8-12 The relevance of the problem caused by the use of heat transfer fluids in various fields of technology in the form of liquid metals. Their use is advantageous in those cases where the required intensive heat transfer from the heated surface, and also in cases provide a high coolant temperature at low pressures. Cooling liquid coolants in metal form combines advantages of gas and liquid cooling. The most suitable heat transfer fluids of this type are the alkali and heavy metals and their alloys. Physical properties of liquid metal are substantially different from those of conventional coolants - gases, water, oil and other liquid metals have greater thermal conductivity coefficient. value lower than the heat capacity; particularly low value of the Prandtl number (Pr=0.005÷0.05). Low values ​​of the Prandtl number Pr explained by a higher coefficient of thermal conductivity, for example, at temperatures (100÷700)°C thermal conductivity coefficient λ sodium Na coctavlyaet order (86÷59) watt/(m·K), and for potassium K-of the order of (46÷28) watt/(m·TO). This study is a logical extension of the above methods for computing^13-25 for the analysis of turbulent flow and heat transfer tubes in the U-shaped flow turbulators (diaphragms) with different relative heights steps for different modes of coolant flow with for a more detailed analysis of the enhancement of heat transfer to heat transfer with small Prandtl numbers specific to liquid metals. Previously, this aspect is practically not been studied.

In this paper, using a fully implicit finite difference schemes centered on irregular oblique grid, a system of Reynolds equations and the energy stored in natural variables. To calculate the pressure field is used SIMPLEC procedure; there is the principle of splitting into physical processes. Approximation convective terms is performed using a quadratic, counterflow scheme. Difference equations are solved using the method of highly incomplete matrix factorization at accelerated convergence method using an additive correction. Multiblock algorithm for solving the problem on a different scale intersecting grids, approved in solving the problems of vortex dynamics and heat transfer,⁸ is used for the correct description of turbulent heat exchange. With zonal Low- Menter model¹² is implemented description turbulent transport. The study looked Channels constant cylindrical cross-section with walls arranged at eight turbulators in the form of periodic apertures semicircular cross section. Parameters varied in the following range: d/D=0,95¸0.92; t/D=0,25¸1, where t-pitch of the vortex; d-diameter of the diaphragm; D-the diameter of the pipe; Re=10⁴¸10⁵-Reynolds number; Pr=1¸20-Prandtl number (for limited calculations-Pr=1¸0.05).

Concise way the calculated model may be characterized as follows. Investigated the calculated three-dimensional region has a plurality of sections, each of which consists of a protrusion (Figure 1). When the calculation it is assumed that when the number concerned vortex turbulent flow becomes steady. In the main part of the study the heat transfer calculation was performed under the boundary condition on the wall of the first kind with Pr=Prandtl number Pr=1 and 0.05 in order to establish patterns of change in the intensification of heat transfer for liquid metal coolant with respect to gas unit Prandtl number. At a preliminary stage of the study carried modification versatile computing complex numerical modeling spatial separated flows and vortex heat exchange in order to adapt and clarify the mathematical model of flow and vortex heat transfer in channels with turbulators on the assumption of occurrence of spatial vortex structures responsible for vortex intensified heat transfer processes in the near-wall areas of tube with turbulence. In order to address the problem of intensified heat exchange the calculated three-dimensional grid is built the same way: designed a two-dimensional grid in the axial and radial coordinates, unfolds circumferential coordinate with a constant pitch. In order to achieve the required resolution in the vicinity of the obstacle we used two-dimensional grid in the form of a multi-tiered structured grids, and the obstacle described in the most detailed grid with the highest spatial resolution. Detailed mesh was inserted into a coarser mesh, with which the described flow in the near wake the obstacles, and the transition region from the wall to the axis is also performed using the intermediate grid, the purpose of which - increase the longitudinal spacing of the grid in the vicinity of obstacles and changes the resolution of the circumferential coordinate.

Later we will not go into details directly modeling aspects of numerical calculations of this technique, as they were described in detail in.^{1,4,8-10,12,14-18,22,25} Experimental confirmation of theoretical data for gaseous coolants and heat transfer fluids in the form of liquid drops was given in^1,2,25,26 which analyzes the actual experiments the authors experiments,²⁷ as well as patterns for limiting the heat exchange.^1,2,25,26 Another confirmation of the obtained calculated numerical data dependencies are analytical solutions for intensified heat transfer obtained by a modified four-layer model of the turbulent boundary layer.^3-7

Figure 1 A pipe grid consisting of several sections with a semicircular turbulizers located in the middle, an inlet and an exit smooth section.

In the input section of the considered portion of the pipe considered uniform flow with a thin boundary layer permitting variation; turbulence parameters correspond to experimental tests in the pipe, assuming scale turbulence pipe diameter of the order of which is selected as the characteristic size and the degree of turbulence is taken equal to one and a half percent. At the outlet section under consideration tube portion are made "soft" boundary conditions, otherwise known conditions continue solutions for which the characteristic parameter is extrapolated area calculation. On washed coolant pipe wall, considered under the boundary conditions of the first kind of isothermal and having a higher or lower for a certain number of degrees in relation to the temperature of the incoming flow temperature, there are no-slip condition. For the chosen geometry of the channel, each individual task of several sections solved two stages: first dynamic problem is solved, then the pre-calculated for the fields constituting the flow velocity and turbulence characteristics thermal problem is solved for various Prandtl numbers. The criteria for dynamic convergence constraint problem are determined by calculating the Cartesian velocity error components and for thermal problem-limiting the increment of heat fluxes on the walls; In this work the value of 0.0001 was adopted for the relative error.

As averaging in direct heat exchange with circular tubes are periodically disposed surface turbulence flow of semi-circular cross-section at turbulent flow of molten metals in various geometrical and operational parameters

coefficient of resistance ξ as averaging and the Nusselt number Nu of semicircular pipes with turbulators in turbulent convective heat transfer for the liquid metal in this work were determined by the calculation method based on a numerical solution of the Reynolds equations closable via shear stresses Menter transfer model, and the energy equation for multiscale intersecting structured grids. Adequacy of the applied method is based on the fact that in comparison to previously^{4,14-19,21-23} were used similar to the experimental data on the heat transfer and hydraulic resistance for tubes with turbulators or semicircular apertures for the flow of air, which took place A good correlation between theory and experiment. Identified in the previous author's theoretical work^{4,14-19,21-23}

value to the experimental data of sales calculation model for local and as averaging the flow characteristics and heat transfer tubes with turbulators causes its application for the purpose of identifying patterns integral (as averaging) of heat exchange tubes in the parameters for the flow of liquid metal with small Prandtl number, depending on the geometry of the channel and the coolant flow regime. In this study, we consider only the most common turbulators semicircular cross section, typical of pipes with diaphragms.

This issue is important because it is necessary to know the level of enhancement of heat transfer-the parameter Nu/NuGL (NuGL-Nusselt number for smooth pipes)-zhidkometellicheskih for coolants, depending on the defining parameters. The classic books on heat exchange intensification^1,2 indicates that the relative experimental data on heat transfer enhancement in the flow of liquid metals do not have enough information, but the authors^1,2 have every reason to believe that the artificial turbulence in the liquid metal flows (Pr<<1) should have a very low efficiency. Calculation intensified heat exchange on the surround to factor control method performed for the most typical of the geometrical and operational characteristics for tubes with turbulators^1,2 for a fairly wide range of Prandtl numbers:

d/D=0.90; 0.91; 0.92; 0.93; 0.94; 0.95; 0.96; 0.97; 0.98; 0.99;

t/D=0.25; 0.50; 1.00;

Re=10⁴; 5x10⁴; 10⁵;

Pr=0,05÷1.

As an illustration of the method of calculation data received by the data in Figure 2 shows the calculated current characteristic line pipe with transverse annular turbulators semicircular cross-section for the considered flow conditions (d/D=0,92; 0,94; 0,96; 0,97; Re=10⁵; t/D=0, 50; Pr=0,05÷1); theoretical streamlines completely similar to the existing experimental data.^1,2 The values ​​of the relative heat exchange Nu/NuGL for various Prandtl (Pr=0,05÷1) ceteris paribus calculated for isothermal flow with equivalent parameters for tubes with turbulators, and without them.

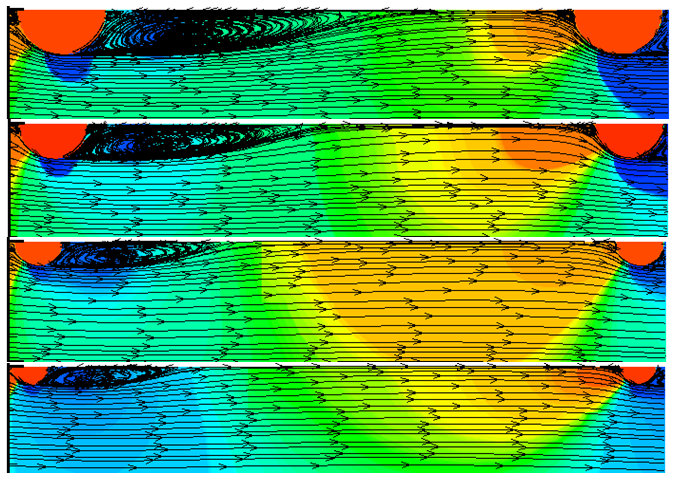
Figure 2 Characteristic current lines for a tube with turbulators of semicircular cross-section under turbulent flow for Re=105, t/D = 0.50 and d/D=0.92; 0.94; 0.96; 0.97 respectively.

For index difference in the levels of enhancement of heat transfer between the liquid metal coolant and gaseous heat carrier is introduced the following set (parameters Pr=0.05 andPr=1 characterized for the largest values ​​Prandtl numbers for gases (polyhydric), and liquid metals (e.g. lithium):

${\overline{\text{Nu}}}_1^{0,05}=\frac{{\frac{\text{Nu}}{{\text{Nu}}_{гл}}|}_{\text{Pr}=0,05}}{{\frac{\text{Nu}}{{\text{Nu}}_{гл}}|}_{\text{Pr}=1}}$        (1)

This complex allows to detect minesimalnoe discrepancy between the levels for the enhancement of heat transfer tubes with turbulators using gaseous or liquid metal coolants. Basic calculation results obtained by the proposed model in the form of the above complex for driving the aforementioned range of defining parameters (${\overline{Nu}}_1^{0,05}$ d/D=0,90÷0,99; t/D=0,25÷1,00; Re=10⁴÷10⁵;Pr=0,05÷1) are shown in Table 1.

Analysis of the data given in Table 1 allows you to do the following. Overall analysis of the calculated data shows that for relatively high turbulators (d/D of the order of 0,90) c small pitch (t/D=0,25) at small Reynolds number (Re=10⁴) decrease in enhancement of heat transfer for liquid metal by relative to gas under otherwise equal conditions may be more than one third (maximum reduction of (35÷40)%); increase above parameters generally leads to a decrease differences between the levels of enhancement of heat transfer between the gas and liquid metal. Therefore, the larger passage with turbulators will be different from the smooth, i.e. with increasing height baffle and reducing the pitch between them, the usually usedólshim will decrease heat transfer enhancement for liquid metal with respect to gas.

This is followed to analyze the dependence (with respect to gaseous coolants ceteris paribus) level of heat transfer enhancement for the liquid metal on the following parameters: the height turbulizer h/D=(1-d/D)/2, the relative pitch of the turbulators t/D and the Reynolds number Re. At low Reynolds number (Re=10⁴) and at high altitudes relative turbulators (d/D≈0.90) remains constant during the transition from the small (t/D=0,25) pitch between turbulators on the average (t/D=0,50) holds first very slight decrease in the complex (it can be said that almost the parameter) and when moving to large pitch (t/D=1,00) there is a noticeable increase in the complex; for medium heights turbulators (d/D ${\overline{\text{Nu}}}_1^{0,05}{\overline{\text{Nu}}}_1^{0,05}$ ≈0.94) during the transition from the small (t/D=0,25) pitch between turbulators on the average (t/D=0,50) holds first very small complex growth (this parameter remains substantially constant) and the transition to large pitch (t/D=1,00) there is a clear increase in the complex; for small heights turbulators (d/D ${\overline{\text{Nu}}}_1^{0,05}{\overline{\text{Nu}}}_1^{0,05}$ ≈0.98) during the transition from the small (t/D=0,25) pitch between turbulators on the average (t/D=0,50) is a reduction of the complex, and during the transition to high pitch (t/D=1,00 ) is an increase in the complex${\overline{\text{Nu}}}_1^{0,05}{\overline{\text{Nu}}}_1^{0,05}$ .

At moderate Reynolds number (Re=5·10⁴) and at high altitudes relative turbulators (d/D≈0.90) during the transition from the small (t/D=0,25) pitch between turbulators on the average (t/D=0,50) and a large pitch (t/D=1,00) there is a clear increase in the complex; approximately the same character occurs for small heights turbulators (d/D${\overline{\text{Nu}}}_1^{0,05}$ ≈0.98); for medium heights turbulators (d/D≈0.94) complex increases slightly, and the transition to high pitch (t/D=1,00) at the transition from the small (t/D=0,25) pitch between turbulators on the average (t/D=0,50) increase complex becomes substantial. ${\overline{\text{Nu}}}_1^{0,05}{\overline{\text{Nu}}}_1^{0,05}$ At high Reynolds number (Re=10⁵) the complex is an increase with increasing steps between t/D turbulators for all heights d/D turbulators. ${\overline{\text{Nu}}}_1^{0,05}$ In the transition from small heights turbulators (d/D≈0.98) to large (d/D≈0.90) at small Reynolds number Re=10⁴ is a reduction of the complex ${\overline{\text{Nu}}}_1^{0,05}$ .

At medium Reynolds numbers Re=5·10⁴ at the transition from small heights turbulators (d/D≈0.98) to the middle (d/D≈0.94) and then to large (d/D≈0.90) at small distance between turbulators (t/D=0,25) there is a first increase of the complex, and then decrease it; analogously: the average distance between turbulators (t/D=0,50) is a reduction of the complex, after which it almost does not increase, and at large distance between turbulators (t/D=1,00) complex is reduced first, then it increases slightly ${\overline{\text{Nu}}}_1^{0,05}{\overline{\text{Nu}}}_1^{0,05}{\overline{\text{Nu}}}_1^{0,05}$ .      

At high Reynolds numbers Re=10⁵ for all values ​​of the relative pitch between t/D turbulators at the transition from small heights turbulators (d/D≈0.98) to the middle (d/D≈0.94) is a reduction of the complex, and during the transition to large (d/D${\overline{\text{Nu}}}_1^{0,05}$ ≈0.90), the height will be an increase in the complex. ${\overline{\text{Nu}}}_1^{0,05}$ Changing complex ${\overline{\text{Nu}}}_1^{0,05}$ depending on the Reynolds number Re ceteris paribus is as follows.

For relatively high turbulators (d/D≈0.90) increase in complex occurs with increasing Reynolds number Re at all relative distance t/D. For relatively medium height turbulators (d/D ${\overline{\text{Nu}}}_1^{0,05}$ ≈0.94) as the Reynolds number increases to Re=10⁴ and Re=5·10⁴ is a reduction of the complex, with a further increase with the Reynolds number Re=5 ${\overline{\text{Nu}}}_1^{0,05}$ ·Re=10⁴ to 10⁵ is an increase in all complex t/D of relative steps. For relatively small height of the turbulators (d/D ${\overline{\text{Nu}}}_1^{0,05}$ ≈0.98) for all relative pitches t/D when the Reynolds number increases to Re=10⁴ and Re=5·10⁴ complex is reduced, then its value remains almost constant ${\overline{\text{Nu}}}_1^{0,05}$ .

As seen from Table 1, in some cases, it occurs when the complex, however, exceeding the level of intensification of liquid metal coolant of the gas is very small, so we can assume that for some cases the level of intensification of the liquid metal tends to gaseous coolants. ${\overline{\text{Nu}}}_1^{0,05}$ Theoretical data revealed patterns relative intensified heat exchange in a wide range of defining parameters for the small values ​​of the Prandtl number, characteristic for the liquid metal, in those areas where there are no reliable experimental data.

1. developed and used in this study calculation method based on the solution of a finite-volumetric method Reynolds equations closable by means of shear transfer model Menter and the energy equation for multiscale structured grids intersecting allowed with acceptable accuracy to conduct calculations of the relative heat exchange tubes in the U-shaped annular vortex generators for liquid metal coolants.
2. The study was conducted analysis of the calculated dependence of the relative heat exchange liquid metal at different relative heights turbulizer h/D, the relative pitch between t/D turbulators, for various values ​​of the Reynolds number Re, ceteris paribus, which shows the qualitative and quantitative changing the calculated parameters.
3. For relatively high turbulators (d/D=0,90) c small pitch (t/D=0,25) decrease in the level of heat transfer enhancement at low Reynolds numbers (Re=10⁴) for the liquid metal with respect to the gaseous ceteris paribus conditions may amount to more than a third; increase above parameters generally leads to a decrease differences between the levels of enhancement of heat transfer between the gas and liquid metal.
4. The data obtained by Intensified heat exchange tubes with turbulators in the turbulent flow reduction prove in terms of heat transfer enhancement ceteris paribus liquid metal with respect to the gas that was previously assumed in the classic papers on the enhancement of heat transfer.^1,2
5. The results obtained in the theoretical data Intensified heat transfer for liquid metals deterministic patterns relative heat exchange in a wide range of characteristic parameters, which does not yet exist experimental material.

None.

The author declares that there is no conflict of interest.

1. Kalinin EK, Dreitser GA, Yarkho SA. Intensification of heat transfer in the channels. Moscow: Engineering; 1972. 220 p.
2. Kalinin EK, Dreytser GA, Kopp IZ, et al. Efficient heat transfer surface. Energoatomizdat; 1998. 408 p.
3. Dreitser GA, Lobanov IE. Modeling isothermal heat transfer in turbulent flow in the channels under the conditions of heat transfer enhancement. Teploenergetika. 2003;1:54‒60.
4. Lobanov IE. Mathematical modeling of the intensified heat exchange in turbulent flow in channels. The Dissertation for the degree of Doctor of Technical Sciences. 2005. 632 p.
5. Lobanov IE. Modeling of heat transfer and resistance in turbulent flow in channels coolants with variable physical properties in terms of heat transfer enhancement. Proceedings of the Third Russian National conference on heat transfer. Moscow: MEI Publishing house; 2002. 144‒147 p.
6. Lobanov IE, Paramonov NV. Mathematical modeling intensified heat exchange when flowing in the channels based on complex models of a turbulent boundary layer. USA: MAI Publishing House; 2011. 160 p.
7. Lobanov IE, Stein L. Prospective heat exchangers with intensified heat exchange for metallurgical production. In Vol III. Mathematical modeling intensified heat exchange in a turbulent flow in the channels using a multilayer and compound models supermnogosloynyh turbulent boundary layer. Russia: Moscow State Academy of Public Utilities and Construction; 2010. 288 p.
8. Ermishina AV, Isaeva SA. The control flow of bodies vortex cells attached to aircraft integrated arrangement (numerical and physical modeling). MSPB; 2001. 360 p.
9. Isaev SA, Leontev AI, Usachov AE, et al. Numerical investigation of jet vortex mechanism intensify heat and mass transfer in the vicinity of the wells on a spherical plane at a flow of its flow of an incompressible viscous fluid with considering the effect of shape asymmetry, natural convection and nonstationary processes. Proceedings of the second Russian national conference on heat transfer; 1998. 121‒124 p.
10. Gosmen AD, Pan VM, Ranchel AK, et al. Numerical methods for the study of viscous liquid. Russia: Mir Space Station; 1986. 234 p.
11. Yu A Bystrov, Isaev SA, Kudryavtsev HA, et al. Numerical modeling vortex enhancement of heat transfer tubes in packets. Shipbuilding; 2005. 398 p.
12. Menter FR. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994;32(8):1598‒1605.
13. Isaev SA, Lobanov IE, Boyarkina OA, et al. Vortex intensification of convective heat transfer under turbulent air flow and the oil in the pipes and ducts with periodic discrete roughness elements. Proceedings of the Fifth Russian National Conference on heat transfer; 2010. 84‒87 p.
14. Dreitser GA Isaev SA, Lobanov IE. Calculation of convective heat transfer in the tube with the periodically arranged surface turbulence flow. High Temperature. 2005;43(2):223‒230.
15. Dreitser GA Isaev SA, Lobanov IE. Calculation of convective heat transfer in a tube with periodic projections. Journal of MAI. 2004;11(2):28‒35.
16. Dreitser GA Isaev SA, Lobanov IE. Calculation of convective heat transfer in a tube with periodic projections. Problems of gas dynamics and heat and mass transfer in power plants: Proceedings of the XIV School-Seminar of Young Scientists and Specialists under the leadership of RAS academician; 2003. 57‒60 p.
17. Isaev SA, Baranov PA, Lobanov IE, et al. Heat and mass transfer and hydrodynamics in swirling flows. The fourth international conference abstracts. Moscow: MEI Publishing house; 2011. 66 p.
18. Kalinin EK, Lobanov IE. Problems of research of heat exchange processes with the currents of single-phase media at the stage of successful development of the numerical simulation. Minsk: Theses of reports and messages VI Minsk International Forum on Heat and Mass Transfer; 2008. 101‒103 p.
19. Lobanov IE, Kalinin EK. Theoretical research, comparison with experiment the flow lines and components of the kinetic energy of turbulent fluctuations in the vortex structures in the tubes with turbulence. Sectoral aspects of technical sciences. 2011;12:4‒15.
20. Lobanov IE. Mathematical modeling of dynamics of vortex structures in the tubes with turbulence. Moskovskoe scientific review. 2013;12:9‒15.
21. Lobanov IE. Modeling the structure of vortex zones between periodic surface arranged turbulence flow of rectangular cross section. Mathematical Models and Computer Simulations. 2012;5(1):63‒74.
22. Lobanov IE. The structure of the vortex zones between periodic superficial turbulence flow of rectangular cross-section. Studies of technical sciences. 2012;2(4):18‒24.
23. Lobanov IE. Theoretical study of the kinetic energy of turbulent fluctuations and its components in the tubes with turbulence. Moscow Scientific Review. 2013;1:23‒30.
24. Lobanov IE, Antyukhov IV. Modern Problems of enhancement of heat transfer in the channels via surface periodically arranged turbulence flow of rectangular cross section. Fundamental and applied problems in Technics and technology. 2013;299(3-2):22‒27.
25. Migai VK. Modeling of heat exchange power equipment. Leningrad branch of Union of Artists of Russian Federation: Energoatomisdat; 1987. 263 p.
26. Migai VK. Improving the efficiency of modern heat exchangers. Leningrad branch of Union of Artists of Russian Federation: Energy; 1980. 144 p.
27. Hustrup RC, Sabersky RH, Bartz DF, et al. Jet Propulsion. 1958;28(4):259‒263.