The velocity of any Keplerian orbiter is well known, but its time derivative is a centripetal acceleration, not an attractive one. Furthermore the rectilinear accelerated trajectory of Newton’s attraction is not part of the Keplerian conics. Newton’s postulate of attraction is therefore not consistent with Kepler’s laws. We demonstrate this geometric reality by the factual kinematics and expose its consequences from the bodies falling, to the rotation speed of the galaxies, passing through Einstein’s equivalence principle or the stability of the solar system.

Keywords: kinematics, laws of Kepler, gravitation, Newton’s attraction, equivalence principle, galaxy rotation

Newton’s postulate of attraction makes the apple falling from the tree with a rectilinear accelerated motion towards the center of the Earth. However the apple is a Keplerian orbiter, but the rectilinear accelerated trajectory is not part of the Keplerian conics.¹ Newton’s interpretation of the gravitation is therefore in conflict with Kepler’s laws.

We will demonstrate here that the kinematics of the Keplerian velocity solves this conflict but this leads to a new interpretation of the gravitation: it does not cause the attraction but the rotation, and the apple falls from the tree on an ellipse, so sharp that it can be confused with a straight line. To intend so, let us first remind that it has been widely demonstrated in the literature that the velocity of a Keplerian orbiter is the simple addition of a uniform rotation velocity and a uniform translation velocity, both coplanar.^2–8 Usually this property is described in the context of an hodo graphic representation of the motion, which makes it rather impractical to manipulate mathematically. We can however give a simple and trivial kinematic expression of this orbital velocity:

$v=v_R+v_T$   (1)

with $v_R=\Vert v_R\Vert =cst and v_T=\Vert v_T\Vert =cst$

where $v_R$ is the rotation velocity and $v_T$ is the translation velocity. Take care, in this expression the index R means “rotation” but not “radial”, while the index T stands for “translation” but not “tangential”. The Figure 1 shows these two velocities on a typical Keplerian orbit.

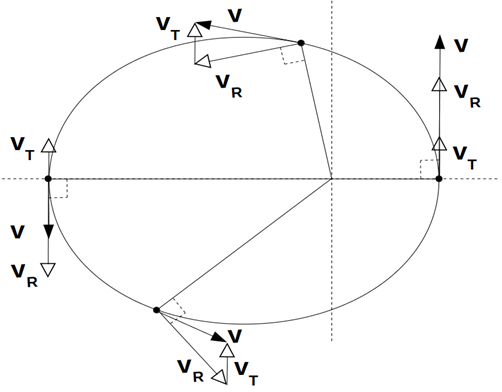
Figure 1 The velocity of a Keplerian orbiter v on a fixed orbit is always the sum of a uniform rotation velocity vR, perpendicular to the vector radius, and a uniform translation velocity vT, which direction is always perpendicular to the main axis of the conic. Both are coplanar and have a constant norm all along the trajectory.

This definition of the orbital velocity is an unmistakable geometric reality, as the authors demonstrated, yet it conflicts with Newton’s postulate of at- traction, as far as its time derivative is a centripetal acceleration, but not an attractive one. And this is problematic because if words have meaning, a centripetal acceleration causes a rotation while an attractive acceleration causes a translation. Without entering the full demonstration that we will run further, let us already give an overview of its consequences. We will show that the conic eccentricity e of any Keplerian motion is simply the ratio between $v_T$ and $v_R$ from the definition $1:e=v_T/v_R$ . From this we see that if the eccentricity is null, it means that $v_T$  is null, and consequently the motion is a uniform rotation. This is the case for instance of the International Space Station (ISS), at a first approximation. Now if we slow down the spaceship by the means of an engine, we will show that $v_T$  is not null anymore and the ISS cannot remain on its circular orbit, it enters an ellipse (0 < e < 1) which focus is at Earth’s center of mass. The higher the slowdown will be, the higher $v_T$  will be and therefore the eccentricity of the orbit, flattening the ellipse. This behavior is well known by the space agencies because it is used to return to Earth the astronauts from a space flight, or to land a rover on Mars.⁹

Now imagine that we could slow down the ISS strongly enough to have $v_T$  close but lower to $v_R$ , in order to have an eccentricity close but slightly lower to 1 (e = 0.9999...). In these conditions the ellipse is strongly flattened and can appear as a straight line if the observer does not have measurement means that are precise enough. The ISS would then look like the apple falling from the tree, straight to the ground at a first approximation. From all this we see that the gravitation does not cause the attraction, but the rotation. What looks like an attraction is a gravitational rotation slowed down by some mechanical constraints. The consequence is that the mechanical and the gravitational accelerations are of different natures, the first causing a translation, the second a rotation, they cannot be equivalent, even locally. We will demonstrate this point in detail, which conflicts with Einstein’s equivalence principle. Before entering the demonstration of all this by the means of the kinematics, we must point out something important. The definition 1 of the orbital velocity is purely kinematic, it embeds no physical parameter like the mass for instance. However its derivative with respect to time leads to Newton’s acceleration that embeds the physical factor GM,¹⁰ G being the universal constant of gravitation and M the mass causing the gravitation. Consequently to the factor GM must correspond a kinematic factor, and we will demonstrate that it is $L{v}_R$ , L being the norm of the kinematic angular momentum (L = r × v) and vR the norm of the rotation velocity from the definition 1. We will see that using the factor $L{v}_R$  instead of GM provides a solution to explain the rotation speed of the galaxies, without dark matter, and suggests that the Keplerian motion could be at work at other scales than the only astronomic one. In the present work we use no postulate, nor hypothesis, we only report the factual reality of the Keplerian kinematics. We will first demonstrate that from the definition 1 of the Keplerian velocity we can get the three laws of Kepler as well as the mathematical structure of Newton’s acceleration. This will provide us a complete set of kinematic equations that will be used as a frame of reference to explore some important consequences, that we started to expose above, and cannot be ignored because they are imposed by the kinematics.

Let us first be more precise about the kinematic definition of the Keplerian velocity 1 coming from the literature. The translation and rotation velocities are coplanar. The rotation velocity vR is the vector multiplication of the frequency of rotation ω, always perpendicular to the plane of rotation, with the vector radius r:

$v_R=\omega \times r$   (2)

Starting from this we are going to demonstrate the existence of Kepler’s laws as well as Newton’s acceleration, or at least its mathematical structure. The first consequence of the expression 1 is the validity of the following one by derivation with respect to time of $v_R$ ($\dot{\omega }$ and $\omega$ being collinear):

$\dot{\omega }r=-\omega \dot{r}$   (3)

The expressions 2 and 3 can help us calculate the derivative with respect to time of the orbital velocity, i.e. the acceleration, which is also simply the derivative of the rotation velocity, because the translation velocity is a constant. The acceleration will therefore be:

$a=\dot{\omega }\times r+\omega \times v=-\frac{\omega }{r^2} \times [r\times (r\times v)]$   (4)

Now defining the mass less angular momentum like R.H. Battin⁹ did as

$L=r\times v$   (5)

the final expression of the acceleration is given by:

$\text{a}= -\frac{L{v}_R}{r^3}r$   (6)

Therefore the acceleration and the vector radius are collinear and this forces the angular momentum to be constant, as awaited for a central field motion:

L = constant  (7)

Note that the expression 6 of the acceleration has the same mathematical structure as Newton’s gravitational acceleration, but it is centripetal. Now from this we observe that the vector product of the rotation velocity with the angular momentum leads trivially to:

$v_R \times L=v^2{}_R \left( 1+\frac{v_R.v_T}{v^2{}_R}\right)r$   (8)

The scalar version of this equation is therefore:

$\frac{L}{v_R} = \left(1+\frac{v_T}{v_R} cos\theta \right)r or p=(1+ecos\theta )r$   (9)

This is the equation of a conic where $p=L/v_R$ is the semi latus rectum,

$e=v_T/v_R$  is the eccentricity and θ is the true anomaly, i.e. the angle between $v_T$  and $v_R$  which is also the angle between the direction of the perigee and the vector radius. This is the expression of Kepler’s first law.

Note that the eccentricity vector is given by:

$e=\frac{V_T\times L}{L{v}_R}$   (10)

Therefore the translation velocity is always perpendicular to the main axis of the conic, which direction is the one of the vector eccentricity. The Figure 1 exhibits both the rotation and the translation velocities at different positions on a conic.

Let us now notice that the scalar multiplication of the total velocity and the vector radius leads to:

$r.v=r.v_T=rr$   thus  $\dot{r}=v_{T}sin\theta$ (11)

Using this last expression it is trivial to show that the angular momentum can be presented as the multiplication of the square of the vector radius and the derivative with respect to time of the true anomaly:

$L=r^2\dot{\theta }$   (12)

This last expression is very well known, being described for instance by L. Landau and E. Lifchitz in their course “Mechanics”.¹ It shows that the areal velocity, defined as $f=r^2\dot{\theta }/2$ , must be a constant as far as the angular momentum also is. Therefore the expression 12 is nothing else but the second law of Kepler.

Note that the time derivative of the true anomaly θ^. and the frequency of rotation ω are related by the following formula:

$\dot{\theta }=\omega \left(1+ecos\theta \right) or r\dot{\theta }=p\omega$   (13)

Now integrating the expression 12 over a complete period T of revolution for an ellipse, as described by L. Landau and E. Lifchitz,¹ and knowing that L and $v_R$ are two constants, we are trivially led to the following formula :

$L{v}_R\text{ = 4}{\pi }^2\frac{{\text{a}}^{\text{3}}}{T^2}\text{=k = constant}$   (14)

This is the expression of the third law of Kepler, where a is the semi-major axis of the ellipse. The simplicity of the above kinematics can be useful in many cases to simplify some gravitational calculations, as orbits or space rendezvous.  All that we presented here is very trivial in terms of kinematics, but it had to be setup in order to expose simply some important consequences of the structure 1 of the Keplerian velocity.

Newton’s acceleration

Newton postulated his gravitational acceleration in order to explain Kepler’s laws, therefore his acceleration must be consistent with the kinematics of the Keplerian motion, i.e. with the velocity defined by 1. The condition to fit both the acceleration 6 and the third law of Kepler 14 with Newton’s postulate is to verify:

$L{v}_R=GM$   (15)

where G is the universal constant of gravitation and M is the mass of the body causing the gravitation.

However the Keplerian acceleration 6 is centripetal, but not attractive as postulated by Newton, even if the global mathematical structure of his acceleration is indeed consistent with the kinematics.

Galileo’s principle of equivalence

The definition 1 of the Keplerian velocity is mass independent, as expected for a motion in a gravitational field, that Galileo has shown to be mass independent.¹¹

Mechanical energy

Calculating the square of the expression 1, with respect to the results of the kinematics analysis, it is trivial to define a kinematic energy, i.e. a massless energy as follows:

${\text{E}}_{\text{M}}\text{ =}\frac{\text{1}}{\text{2}}{v}^{\text{2}}-\frac{L{v}_R}{\text{r}}=\frac{\text{1}}{\text{2}}{v}^2{}_R{\text{(e}}^{\text{2}}\text{ -1)}$   (16)

Multiplying this last expression by the mass of the orbiter, and considering the formula 15, we get directly the usual expression of the mechanical energy as described in classical mechanics,¹ with its kinetic and potential parts.

Falling bodies

What we call a falling body is a body that is accelerated on a straight line towards the center of the planet. Usually this experiment starts with a fixed body that is freed to fall at a time, so let us take the example of the apple falling from the tree.

At start the apple is fixed to the tree and therefore has no orbital velocity, but it is however a Keplerian orbiter. The only way to achieve this from the definition 1 is to have:

$v_R=-v_T$   (17)

This means that the apple is indeed submitted to the gravitational rotation velocity $v_R$ from the Earth, but it cannot move because the translation velocity $v_T$ opposes to it. From 14 and 15 we get the rotation velocity $v_R=GM/L$ , were M is Earth’s mass, i.e. if the mass M exists then $v_R$ exists, and the apple cannot get rid of it. If $v_T$  would be null, the apple would orbit around the Earth at nearly $v_R$  7.9103m/s, but it is not, because $v_T$ is as big as vR, but of opposite direction, this is the only way to have a null orbital velocity.

But what is $v_T$ ? Exactly as vR is the integral of the gravitational acceleration 6, $v_T$ is simply the integral of the acting accelerations that are not gravitational, like frictions for instance. Actually the apple is not alone to wish to gravitate freely around the planet, the tree would also like to, as well as the ground, and so on. There are so much particles that would like to gravitate around Earth’s mass center that there is a traffic jam and all the particles are blocking each other, constituting the Earth.

Let the initial translation momentum of the apple on the tree be $P_T=m{v}_T=m{v}_R$ , now if the apple disconnect from the tree, in a fraction of a second, it cannot get rid of this tremendous initial momentum ($v_R\approx$ 7.9103m/s multiplied by the mass of the apple), and otherwise the apple would be submitted to a tremendous force that would smash it. Actually the apple can only get rid of a very small portion of its translation momentum to get:$P_T=-m{v}_R\left(1-ϵ\right)$ where $ϵ$ is very small. But mean while $v_R$ still exists and acts, consequently the orbital velocity is not null any more $v= v_R+v_T\ne 0$ , i.e. the apple falls on a Keplerian conic which eccentricity is very close but lower to $1:e=v_T/v_R=1ϵ=\mathrm{0.99999...}$ Such a conic is a very sharp ellipse which focus is at Earth’s center and apogee is at the altitude of the branch of the tree, with a minor axis which dimension is barely measurable because the mass of the apple is so small in regard of Earth’s mass. Such a trajectory can be confused with a straight line, but this is an illusion. Actually the earth would be transparent with all its mass concentrated on a single mathematical point, Newton’s postulate would make the apple falling until it get stuck on this point while the kinematics forecast that the apple would orbit around this point, before going back to its starting position.

Mechanical versus gravitational accelerations

Let us consider an orbiter on a perfect circular orbit, so having $v_T$ = 0. Its acceleration is of course given by the expression 6. Let us now apply a mechanical force F provided by an engine, the total acceleration will then become:

$\text{a}= -\frac{L{v}_R}{r^3}r+\frac{F}{m}$   (18)

Where m is the mass of the orbiter. Integrating this expression must lead to the expression 1 of the velocity. We shall therefore verify:

$v=v_R+v_T$   with $v_T= {\displaystyle \int \frac{f}{m}}dt$  and  $v_R=\omega \times r$ (19)

At this point it is important to note that the mechanical acceleration can only provide a translation. Indeed a force must have a physical connection to the axis of rotation to cause a rotation, but the mechanical force provided by the engine has no physical connection to Earth’s mass center, and thus to the gravitational axis of rotation. As far as the engine has been used $v_T$ cannot remain null, and therefore the mechanically accelerated orbiter cannot remain on a circular orbit because the eccentricity of its conic is not null any more $\left(e=v_T/v_R\ne 0\right)$   whatever the direction or the intensity of engine’s thrust. This is a reason why the calculations of space rendezvous are so complex to solve. No engine has ever been able to simulate the gravitational rotation, as short and tiny the thrust of the engine was. Provided that the spaceship is in a gravitational field, no successive short mechanical thrust can simulate a circular orbit around the Keplerian focus.⁹

Exactly as we described for the falling bodies, we have to make a clear distinction between the gravitational acceleration and the mechanical one. The first provides the rotation and the second the translation. These two accelerations are therefore of different natures, in no way we can say that they are equivalent, even locally. This fact conflicts with Einstein’s principle of equivalence, at least as described in his articles of 1907 and 1911. Indeed in 1907 Einstein explained:¹² “We consider two frames of reference, Σ1 and Σ2. Let Σ1 be accelerated in the direction of its X coordinate axis, and let γ be the (time-constant) value of its acceleration. Suppose that Σ2 is at rest, but located in a homogeneous gravitational field, which imparts to all objects an acceleration γ in the direction of the X axis. As far as we know, the physical laws with respect to Σ1 do not differ from those with respect to Σ2; this derives from the fact that all bodies are accelerated in the same way in the gravitational field. We therefore have no reason to suppose in the state of our experience that the reference frames Σ1 and Σ2 differ in any way, and we will therefore assume in what follows the total physical equivalence between the gravitational field and the corresponding acceleration of the frame considered.” As far as the gravitation would cause the attraction, this presumption could be correct indeed, but since the gravitation causes the rotation while the mechanical acceleration causes a translation, it cannot be correct. No attractive acceleration could ever be equivalent to a centripetal acceleration.

In 1911 Einstein added:¹³ “By theoretically considering processes that take place relative to a uniformly accelerated reference frame, we obtain information on the occurrence of localized processes in a homogeneous gravitational field. The principle of equivalence does not affirm that it is possible to produce any gravitational field (for example that associated with the Earth) by means of the acceleration of a reference frame. It only asserts that the properties of a physical space, as they present themselves to us from the point of view of an accelerated frame of reference, constitute a particular case of the gravitational field.” Here again, this could only be true if the gravitation would cause the attraction, but is not correct as far as it causes the rotation. An attractive acceleration cannot be a particular case of a centripetal acceleration. If we remind Einstein’s thought experiment of the observer in a lift cabin,¹⁴ who would like to know if the acceleration he is feeling is provided by some mechanical means or by his position on a planet, he will be able to distinguish both situations, contrarily to what Einstein postulated. In the first case a ball dropped to the floor will fall on a straight line, in the second case on an ellipse. However the more massive the planet will be, the more precise his measurement means must be.

Stability of the solar system

As long as the Sun will have a mass M, it will provide a rotation velocity $v_R=GM/L$ to all the bodies in its gravitational field. If no mechanical force provides a $v_T$ superior or equal to vR, the body will eternally be trapped into Sun’s field. The situation of a planet is somehow similar to the one of an electron in an atom: until you provide at least the ionization energy to the electron, it remains trapped into the atom. The only way to eject a body from Sun’s influence, is to provide it $v_T\ge v_R$ , and in this case the trajectory becomes a parabola (e = 1) or an hyperbola (e > 1), which focus is still the Sun. But of course ejecting a planet like the Earth, moreover Jupiter, will require a tremendous force to increase $v_T$ enough to be superior or equal to $v_R$ . Such an event could always happen at long term, but it would require some very exceptional circumstances. Now that the solar system is stable, what currently happens are relatively light chocks usually coming from the crash of asteroids on the planets. Each one causes a slight modification of the translation velocity, so a slight modification of the orbit eccentricity, the orbit is deformed but is still stable. Therefore there is no evidence that the solar system could become chaotic¹⁵ at neither short nor long term. The gravitation creating the rotation ensures the stability.

Rotation of the galaxies

Vera Rubin has shown that the stars inside the disks of the galaxies have a velocity incompatible with the Newton’s theory of the gravitation.¹⁶ The Figure 2 gives a typical example of what is expected from the Newton’s postulate and what is actually measured for spiral galaxies.²¹

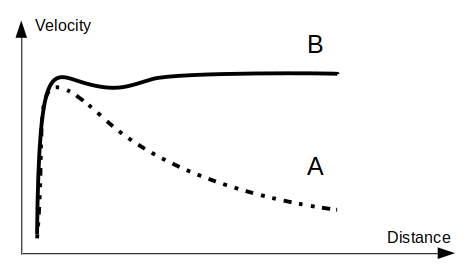
Figure 2 Typical velocities of the stars in a spiral galactic disk with respect to their distance to the center of the galaxy. The doted curve A is the one expected with Newton’s theory, the plain curve B is what is actually measured.

At a first approximation we can consider that the stars in the spiral galactic disk have a circular orbit and their velocity is given by the third law of Kepler 14:$v=\sqrt{k/r}$ For Newton the numerator k = GM = constant, and consequently the velocity must decrease when the distance r increases.  But for the kinematics $k=L{v}_R=L\omega r$ , therefore $v=\sqrt{L\omega }$ and the velocity can remain constant whatever the distance, at the condition that $L\omega$ also is. As far as $L\omega$ has the dimension of a mass less energy (energy divided by the mass of the orbiter), if the stars of the galactic disk are populating the same mass less energy level $E=L\omega$ , they will have the same velocity independently of their distance to the center of the galaxy, and the curve B of the Figure 2 can be explained. The kinematics can therefore explain the experimental measures without dark matter, but considering that the galaxies are structured around some energy levels that are mathematically analogous to a macroscopic version of the Planck-Einstein relation¹⁷ $E=h\nu$ .

Considering the kinematics of the Keplerian velocity we were able to demonstrate that the gravitation causes the rotation but not the attraction, a body falls on an ellipse but not a straight line, the mechanical and gravitational accelerations are of different natures, the solar system must be stable, the rotation of the galaxies can be explained if the stars in the disk occupy the same mass less energy level. It is important to note that to achieve so we used no postulate, nor hypothesis, but only the pure factual kinematics.

The results that we get open some new perspectives, especially when considering the Newton’s “universal” constant G. Newton did not know the existence of the electric charge, neither of the galaxies, nor of the atoms. What he called “universe” contained only the macroscopic bodies of the solar system. It would then be anachronistic to consider that his definition of what is “universal” also applies to what he did not even suspect. Sure G is a universal constant in his restricted universe, but is it still at any scale in our nowadays universe? Indeed we can notice that Coulomb’s acceleration has the same mathematical structure as Newton’s acceleration, but Coulomb’s factor¹⁸ $-q^2/4\pi {ϵ}_{0}re-$ places the factor GM. From a kinematic point of view if we have $L{v}_R=GM$  at an astronomic scale, nothing is opposed to have $L{v}_R=-q^2/4\pi {ϵ}_0$ at an atomic one. Indeed $L{v}_R$ is a kinematic factor without any physical constraint, at the contrary of the factors postulated by Newton and Coulomb. So we may wonder if Kepler’s laws could also be at work at an atomic scale.

Here we have to remind Rutherford’s proposal to describe the electron around the proton like a planet around the Sun,¹⁹ and the criticisms against his model: the electron being in rotation it is submitted to a centripetal acceleration, and therefore as a charged particle it must emit photons, so lose energy, making the atom unstable. But this argument was unfair because if the electron is really like a planet, it must be in weightlessness, therefore it feels no acceleration and emits nothing, like the astronauts inside the ISS, it is then on a stable trajectory similar to those necessary to Bohr’s model.¹⁸ We are then led to wonder if a quantum version of the Keplerian motion could explain the electrons behavior in the atoms at some extent. This perspective has to be investigated. The General Relativity (GR) also uses the factor GM, and reduces to Newton’s theory for low masses and velocities.²⁰ It might then be interesting to introduce the factor $L{v}_R$ instead of GM in the GR, in order to see if it could work at other scales than the astronomic one. Furthermore the only theory that we own to explain the weightlessness is the GR, so if we have to consider an electron in weightlessness around the proton, the GR might be useful. This perspective has also to be investigated.

Even if we dared here to criticize the postulates of Newton and Einstein, constructively we hope, we also propose that answering to these criticisms by respecting the kinematics, could lead to improve and extend their theories. In no way at all a kinematic demonstration could ever be a theory of the gravitation, so what we exposed here cannot compete with Newton’s and Einstein’s theories, this is not our point at all. What we point out is that our current theories of the gravitation must be consistent with the kinematics of the Keplerian motion, thus with the orbital velocity 1, but they are not so far.

None.

The author declares that there is no conflict of interest.

1. Landau L, Lifchitz E. Mechanics. Mir editor. Moscow; 1966.
2. David Derbes. Reinventing the wheel: Hodographic solutions to the Kepler problems. Am J Phys. 2001;69:481.
3. Eades JB. Orbit information derived from its hodograph. NASA. 1968.
4. Hamilton WR. The hodograph, or a new method of expressing in symbolic language the Newtonian law of attraction. Proc R Ir Acad III. 1847;344–353.
5. Abelson H, Di Sessa A, Rudolph L. Velocity space and the geometry of planetary orbits. Am J Phys. 1975;43:579–589.
6. Gonzalez-Villanueva A, Nunez-Yepez HN, Salas-Brito AL. In veolcity space the Kepler orbits are circular. Eur J Phys. 1996;17:168–171.
7. Apostolatos TA. Hodograph: A useful geometrical tool for solving some difficult problems in dynamics. Am J Phys. 2003;71:261–266.
8. Butikov EI. The velocity hodograph for an arbitrary keplerian motion. Eur J Phys. 2000;21:1–10.
9. Battin RH. An Introduction to the Mathematics and Methods of Astrodynamics. Revised Ed. Reston: American Institute of Aeronautics and Astronautics, Inc; 1999.
10. Douglas W MacDougal. Newton’s Gravity. New York: Springer Science Business Media; 2012.
11. Adler Carl G. Galileo and the Tower of Pisa experiment. Am J Phys. 1978;46(3):199–200.
12. Einstein A. On the principle of relativity and the conclusions drawn from it. Radioactivity and Electronics. 1907;4:411–462.
13. Einstein A. On the influence of gravity on the propagation of light. Annals of Physics. 1911;35:898–908.
14. Marzari A, Tommaso R, Onorato P. Three experiments on the Einstein’s lift. Eur J Phys. 2021;42:045404.
15. Laskar J. Large-scale chaos in the Solar System. Astron Astrophys. 1994;287:L9–L12.
16. Rubin V. A Century of Galaxy Spectroscopy. Astrophys J. 1995;451:419–428.
17. Richard Feynman P. The Feynman Lectures on Physics. Vol III. 1964.
18. Feynman Richard P. The Feynman Lectures on Physics. Vol II. 1970.
19. Rutherford E. The Scattering of α and β Particles by Matter and the Structure of the Atom. Philosophical Magazine. 1911;21(125):669–688.
20. Wald Robert M. General Relativity. University of Chicago Press; 1984.
21. Begeman KG, Broeils AH, Sanders RH. Extended rotation curves of spiral galaxies: dark haloes and modified dynamics. Monthly Notices of the Royal Astronomical Society.1991;249:523–537.