eISSN: 2576-4500


Research Article Volume 1 Issue 4
Fraunhofer Institute for High-Speed Dynamics, Ernst-Mach-Institut, Germany
Correspondence: Robin Putzar, Fraunhofer Institute for High-Speed Dynamics, Ernst-Mach-Institut, Freiburg, Germany , Tel +49 761 2714-417
Received: December 11, 2017 | Published: December 22, 2017
Citation: Gulde M, Berger H, Putzar R. Stereoscopic imaging determines space debris impact crater distribution and morphology. Aeron Aero Open Access J. 2017;1(4):157-160. DOI: 10.15406/aaoaj.2017.01.00021
A two-step methodology based on imaging a spacecraft target surface in orbit is analyzed, which is capable of counting impact craters and determining their morphology. The methodology can be used to measure impact flux data and subsequently improve near-Earth particle environment models like MASTER and ORDEM. Craters are detected by a surface scan in a first step, and the morphology of selected craters is determined using stereoscopic images in a second step. To analyze the methodology, impact craters were modeled using Blender, visualized through MonoGame and the generated images analyzed with MATLAB using generic camera parameters. Optimum camera settings were derived for the particular scenario. For identification of the craters, the camera should be placed within 1.2m of the surface. To determine the full, three-dimensional crater morphology, the camera needs to be placed much closer to the target surface. Both a rotation and a translation movement of the camera were investigated for recording the stereoscopic images. However, in view of the applicability of the method to map spacecraft surfaces, the translational movement is found to be more feasible to implement and less sensitive to inaccuracy during the positioning of the camera. In particular, a translation of the camera by about 0.4times the target crater radius minimizes the sensitivity to misalignment of the camera. Improved particle environment models allow for more precise risk estimation for any future space mission, helping to save the lives of astronauts as well as preserving investments in space infrastructure.
Keywords: space debris, hypervelocity, impact, crater, stereovision, morphology, impact flux measurement
Impacts of fast traveling natural micrometeoroids and anthropogenic space debris are widely considered as one of the two major threats to humankind’s presence in near-Earth space. The dimensions of particles that pose an impact threat to spacecraft range from micrometer-sized micrometeoroids to the 8.5-ton Tiangong-1,1 which will re-enter in early 2018 to be superseded by the 8-ton Envisat.2 Larger objects are being tracked3 and cataloged,4 so that collision avoidance maneuvers can be performed.5 The size of objects in the NASA catalog ranges down to ten centimeters.6 For impacts of smaller objects, collision avoidance maneuvers are not feasible since orbit parameters are generally not available. To cope with the hazard from such smaller sized particles, risk analyses are being performed routinely for spacecraft,7 which rely on particle environment models like MASTER and ORDEM.8 The refinement and update of such models require impact flux data, which can be generated by in-situ detectors9,10 as well as the analyses of retrieved hardware.11,12 Typical unmanned spacecraft structure walls can withstand particles up to about one millimeter in size,13 while the ballistic limit of manned modules is usually between one and two centimeters.14 For unmanned spacecraft, impact consequences reach from component degradation15 to mission loss,16,17 which is generally associated with an economic risk.18 For any manned missions, however, the particle environment poses a constant threat, which might inflict a loss of crew members or the entire crew. Therefore, generation of impact flux data is crucial not only to calculate and reduce the economic risk for unmanned missions but also to reliably evaluate the risk for astronauts while in orbit.
Determining the properties of an impactor from the resulting impact feature is generally considered non-trivial. Apart from the crater diameter, information on the depth and shape of a crater helps to identify the physical properties (e.g. density ratio between impactor and target surface material) and shape of the impactor19,20 as well as impact direction.21,22
Here, we propose a two-step methodology to count impact craters on spacecraft surfaces and determine their morphology. The approach is based on imaging a spacecraft target surface with a camera, while the spacecraft is in orbit. In the first step, craters are being detected by a surface scan with the camera. In the second step, stereoscopic imaging with the same camera is used to determine the morphology of selected craters. For the evaluation of the approach, a generic scenario with respect to the camera parameters has been assumed. The aim was to (1) determine optimal recording settings to find as many craters as possible within the shortest amount of time and determine their diameter with a maximum error of 10%, and to (2) investigate the optimum scenario for deducing three-dimensional crater profiles with minimum error.
The camera parameters are chosen to be conservative, assuming that imaging shall be performed while the spacecraft surface is in orbit. In principle, the approach can also be used for post-flight analysis. However, it is assumed that ground-based diagnostics by far exceed the possibilities available in orbit, demanding a re-evaluation of the findings for higher resolution imaging.
The impact craters were modeled using Blender (https://www.blender.org) and visualized through MonoGame (http://www.monogame.net) using the camera parameters as given in Table 1. Subsequently, we performed the camera calibration as well as image analysis within the MATLAB (https://www.mathworks.com) programming environment.
For generality, we assumed the crater to be located on a planar aluminum surface and to be of half-spherical shape with its depth equal to its radius. Furthermore, we chose the texture of the undisturbed surface to be slightly darker compared to the texture inside the crater. This accounts for the fact that most spacecraft hulls are made from aluminum. An impact will remove the oxidized surface material and expose the brighter, sub-surface aluminum which cannot oxidize in outer space.
We rendered the final model as seen by the camera in both positions employing MonoGame with basic lighting options, i.e. using only diffusive and ambient lighting. For this initial study, we used the raw output images with the resolution as given by the camera parameters and avoided further image manipulations including antialiasing or normal mapping. Even though we use a software camera instead of a real camera, a calibration is still necessary. However, as may be expected, the resulting distortions are well below one pixel, such that a substantial influence on the results is very unlikely.
To determine the optimal camera parameters for the investigation of the crater size distribution, we scanned the image for pixel intensity deviations. In order to separate the foreground (the crater) from the background (the surrounding aluminum plate), we treated the image as a grayscale histogram and employed an Otsu algorithm to find the optimal threshold.23 With the background removed, we receive a binary image and sum its individual image lines to obtain the maximum crater diameter (Figure 1).
Next, we translate the resulting crater diameter into physical units using the respective camera parameters. Lastly, the found crater diameter is compared to the diameter of the model to estimate the measurement error.
To reconstruct the three-dimensional shape of a crater found by means of the previously described method we employed a stereoscopic approach using one camera. In this scenario, the same camera records two images of the crater from two different positions. Usually, four steps are necessary to obtain the depth information of the crater.24 First; we need to find features in the images. Next, the features have to be matched between the two images. Furthermore, we need to determine the camera parameters. Lastly, we calculate the distance of each of the detected and matched features using a trigonometric approach (Figure 2). Within the scope of the current study, we assume knowledge of the camera parameters, since we use them as input parameters, and hence omit the respective step. When applied in a real scenario, the cameras parameters will not be known with perfect accuracy and hence need to be estimated.25
For the first task, we employ a Harris and Stephens corner detection algorithm.26 This feature detector finds corners based on the intensity gradient within images and is applied to the first camera image only. We then track the detected features in the second camera image using the Kanade-Lucas-Tomasi approach.24 This approach assumes a constant optical flow in the neighborhood of the respective feature´s pixels and solves the optical flow equations for all nearby pixels. In the last step, the depth information is calculated using the resulting trigonometric system as depicted in Figure 2a.
As shown in (Figure 2b) (Figure 2c), we investigated two types of movements from the camera in order to find the optimal relative camera orientations and positions with respect to reconstructability of the crater morphology. Either, we rotate the camera by a predefined angle between images (Figure 2b) or translate the camera position by a vector t.
To quantify the error of the reconstruction in the stereoscopic approach, we computed the deviation d of the depth coordinate z for each point in the reconstructed model:
Here, N is the total number of points in the reconstructed model and and are the z-coordinates of the nth modeled and reconstructed crater point, respectively. Notably, we rotated and translated the reconstructed model such that the deviation became minimal.
For both, the measurement of the crater diameter as well as the crater morphology, the resulting error was normalized with respect to the characteristic dimension. In case of the diameter determination, the error is the ratio between the model crater and the reconstructed crater. For the three-dimensional model, the error is normalized by the crater model depth.
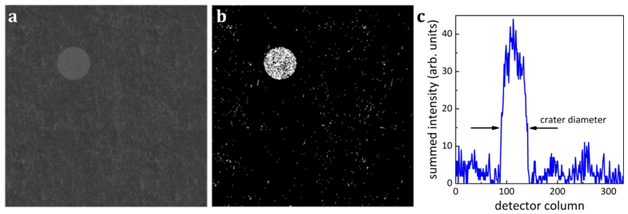
Figure 1 Crater diameter determination methodology a) Exemplary crater image b) Binary image after Otsu threshold application c) Collapsed image with resulting crater diameter in camera units.
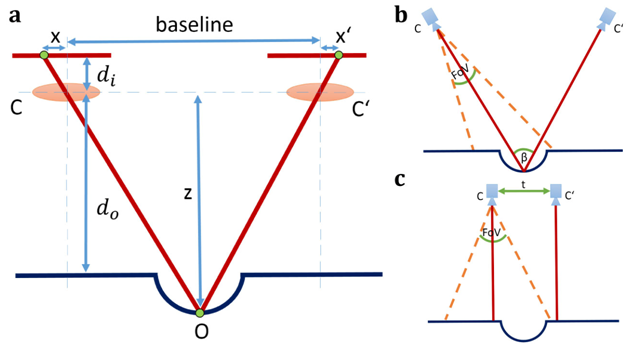
Figure 2 Simulation setup and scan modes. a) Cameras C and C’ project point O inside the crater at positions x and x’ on the detector, respectively. Knowledge of the image distance di and object distance do as well as the baseline allows to compute the depth information z. b) Camera with field-of-view FoV continuously points at target, rotates by angle . C) Camera translates parallel to spacecraft surface by distance t between images.
First, we investigated the maximum camera distance from the crater to estimate a crater diameter of 1mm within 10% accuracy. Figure 3a displays the relative error of the measured crater diameter as a function of camera distance. As is to be expected, the reconstruction becomes less accurate for larger camera distances. Up to 1.2 m, the relative error is at or below 10%. At this distance, an image represents a physical area of 13x17cm2.
In order to extract three-dimensional data from the pair of stereoscopic images, the camera needs to be closer to the crater. Figure 3b displays the relative error of the reconstruction as function of the distance between the camera and the crater. Above a distance of 0.15m, the relative error increases dramatically. This effect can be accounted to the minimally required number of points needed for a three-dimensional reconstruction. Since the pixel number at even larger distances became too small to account for minute changes in the morphology, we decided to stop the reconstruction at this point.
As displayed in (Figure 2b) (Figure 2c), we analyzed two different recording modes for the generation of the stereoscopic images. In the first mode, the camera is rotated around the target crater by an angle before taking the second image. In the second mode, we translate the camera by a vector parallel to the spacecraft surface before the second image is taken. (Figure 4a) (Figure 4b) display the relative error as a function of rotation angle and translation of the camera, respectively.
In the case of small angles, the changes between the stereo images are too small to allow for a precise reconstruction. On the other hand, image distortion increases with angle, making feature tracking at larger angles more challenging. Hence, there exists an optimal range of rotation in which the reconstruction is least prone to errors. With the parameters of the current study, we found this range to lie between 3 - 7°, as indicated by the dashed red lines in Figure 4a. While the error offset changes with the overall distance between the camera and target, this optimal regime is qualitatively not influenced by the distance.
Since the rotation of the camera around a predefined point is mechanically challenging, we also investigated translational movement without changing the camera pointing. This scenario might be more realistic for the actual application of the approach. Since the translation vector is a function of the object size under observation, we normalized the translational shift by the crater radius. As in the previously discussed case, we expect the curve to have three regimes. For small translations the changes in the image pair will be too small to be detected in a rasterized pixel graphic, leading to a large reconstruction error. The feature tracking will suffer, however, from large image shifts. The optimal region will lie in between and is found to be between 0.3 and 0.6 crater radii for the parameters used in this study, as depicted in Figure 4b indicated by the dashed solid lines. Similar to the rotational case, only the error offset is influenced by the overall distance between camera and target, but not the optimal regime.

Figure 3 Relative measurement error as a function of camera distance. Model crater diameter is 1mm. The dashed red line indicates an error of 10%. a) Crater diameter measurement. b) Morphology reconstruction.

Figure 4 Optimal camera position and orientation. Model crater depth equals the crater radius. Optimal regimes between dashed straight lines. a) Relative estimation error as function of camera rotation. b) Relative estimation error as function of camera translation, normalized to crater radius.
Resolution |
720 x 486 (NTSC) |
Field of view |
8.1 deg (h) x 6.1 deg (v) |
Bit depth |
8 |
Table 1 Camera parameters as used in the simulation
The investigated method is capable of determining the crater size distribution as well as crater morphology. For the generic camera model in this work, we found a maximum distance to the target of 1.2m to reconstruct the impact crater diameter within 10% accuracy.
As expected, to determine the crater morphology, the camera needs to be placed much closer to the target surface. We investigated two different approaches and found similar error levels for both, rotational and translational camera movement between the recordings of the stereoscopic images. However, in view of the applicability of the method to map spacecraft surfaces, we believe that the translational movement is more feasible to implement and will be less prone to inaccuracy during the camera positioning. In particular, we suggest translating the camera by about 0.4times the target crater radius to minimize the effect by misalignment of the camera.
The different target surface distances for crater identification and crater morphology determination motivate the proposed two-step methodology, allowing an initial scan to record the crater diameter distribution at a relatively large distance. A second, close-up scan of regions of interest then provides the crater morphology data.
Any impact flux data generated with the proposed methodology helps to improve the available particle environment models. This leads to a more precise estimation of the risk for any future space mission and can have a direct impact on the protection measures realized for future spacecraft and may also allow for structural mass savings in future missions. Therefore, application of this methodology can not only help to save investments in space infrastructure but also to better estimate the risk for future manned missions, which may save the lives of future astronauts.
We would like to thank M. Schimmerohn and D. Sholes for helpful discussions.
The authors declare no conflict of interest.

©2017 Gulde, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.