The modernization of GNSS (Global Navigation Satellite System) with the inclusion of new constellations and improvements in the already available systems has been assessed with great interest over the last decade. The combination of different satellite constellations expands the possible applications, so the term multi-GNSS appeared to designate the use of these multiple navigation systems. On that topic, one important element is the quality of the broadcast messages made available by each system to determine the satellites’ coordinates that will be used to calculate the user’s position and how much this information can be trusted. When merging systems for multi-GNSS, the Russian constellation, GLONASS, is still an outsider when the combination of systems is discussed. After regaining its full constellation in 2012 some studies have been conducted on efforts to increase the knowledge about its functionality. This paper discusses the step size needed for the Runge-Kutta 4th order, indicated to be used on the ICD documentation, interpolation that gets the coordinates of the satellite, and impacts on computational processing time, which has not been previously addressed in the literature. Three days of broadcast ephemeris were processed and compared with IGS final products to determine the residual mean squared error for the local components. It was tested steps of 0.1, 1, 2, 10,30, 45, 60, and 120 seconds, and the step of 1 second was determined as the best one. With the analyzed ideal step-size, as a result of this paper, a Python 3.8 library was made available for users to include on their own projects.

Keywords: GLONASS, Runge-Kutta, broadcast message

The emergence of GNSS (Global Navigation Satellite System) has brought about a revolutionary change in the field of positioning activities. The initial GNSS systems, namely, the Russian GLONASS (Global Navigation Satellite System) and the American GPS (Global Positioning System), were fully developed and implemented by 1995.¹ Subsequently, two more systems were created, the BDS by China and Galileo by Europe, thereby providing a total of four operational GNSS systems presently available.² Each GNSS system comprises three key components, namely, the ground, space, and user segments.³

GLONASS, a Global Navigation Satellite System, has been developed and deployed with three generations of satellites throughout its history. The first generation of satellites was launched in 1982, followed by the GLONASS-M satellites launched since 2003 and GLONASS-K introduced in 2011, according to Jerez.⁴ As of February 15th, 2023, the GLONASS system consists of 24 operational satellites and one undergoing the commissioning phase, as reported by the GLONASS Information and Analysis Center (https://www.glonass-iac.ru/en /).

Although GLONASS and GPS are both GNSS, they differ in their structures. GPS uses the latest realization of WGS84 (World Geodetic System 1984) as the reference frame, while GLONASS uses PZ90 (Parametry Zemli 1990). Despite the similar realization of both systems, such as the origin being earth's centre of mass, the Z-axis pointing to the Conventional Terrestrial Pole (CPT), the X-axis pointing to the terrestrial equator on the origin meridian, and the Y-axis completing the dextrogyre system, there are still some differences in their materialization and adopted ellipsoids. CDMA (Code Division Multiple Access) is used for the signal structure of GPS, while GLONASS still relies on FDMA (Frequency-division multiple access) for all its legacy satellites. However, in the GLONASS signal evolution plan, new CDMA signals have been made available to users as a complement to the legacy FDMA signals. The introduction of CDMA signals is expected to improve navigation accuracy, resistance to interference, and separation of open and authorized services. The first CDMA signal in the L3 band was made available since 2011, and additional signals will be added with each new generation of GLONASS satellites.⁵

A further contrast between GNSS systems pertains to the dissemination of the broadcast ephemeris, which is essential for satellite coordinate determination. Differently of GLONASS, all other GNSS systems provide ephemeris data through Keplerian elements and their perturbations. GLONASS, however, distributes ephemeris data via Cartesian elements that comprise the satellite's state, velocity, and acceleration vectors.^5,6 The computation of GLONASS satellite coordinates was first addressed by Stewart and Tsakiri⁷ in a study that discussed orbital forces and provided a detailed explanation of the numerical integration method. The study analyzed the influence of time steps on the computation process and the degradation of accuracy for periods over those recommended by the ICD in 1998. However, due to the decreased number of satellites in the early 2000s (Figure 1), few studies were published on this topic during that time. Chao and Gick⁸ analyzed the long-term weather effects on the system's eccentricity and proposed mitigation strategies. Most of the studies conducted during this time focused on the combination of GPS and GLONASS in various positioning techniques.^9,10

Figure 1 GLONASS satellites in constellation through the years.
Source: Adapted from Jerez et al.,¹ and Russian Space Systems.⁶

Following the restoration of a complete constellation in 2011, a new wave of research on GLONASS emerged. Statella et al.,¹¹ conducted a study using a short period of data to determine the accuracy of the ephemeris, obtaining a mean discrepancy of 6.53 meters. Maciuk¹² examined three approaches of the Runge-Kutta method (4th, 5th, Fehlberg 4th and 5th order) for solving satellite motion. Zhang et al.,¹³ analyzed one week's data of all healthy orbiting satellites and identified significant periodic variations in the errors. Heng¹⁴ investigated anomalies and User Range Error (URE) accuracy at that time and observed that the performance of GLONASS did not match that of GPS in terms of URE and ephemeris accuracy. Nonetheless, the GLONASS Signal-In-Space (SIS) did exhibit an improving trend, particularly in terms of constellation strength, anomaly probability, and the occurrence of simultaneous multiple anomalies.

This study aims to investigate the impact of step size on the accuracy of calculated coordinates using the 4th-order Runge-Kutta interpolation method, as well as its effects on the processing time. To the best of our knowledge, this topic has not been previously addressed in the literature. In conjunction with the findings of this research, a Python 3.8 library containing the algorithms for calculating GLONASS satellite coordinates will be made available. The structure of this paper is outlined as follows: In the chapter 2, details of the GNSS ephemeris are provided. Chapter 3 presents the formulation and current state of the 4th-order Runge-Kutta method. The methodology and results are discussed in chapter 4. Finally, in chapter 5, the final conclusions and remarks are presented.

GNNSS Ephemerides

In the realm of satellite navigation systems, the transmission of broadcast coordinates information holds utmost significance as it allows the users to compute the location and speed of the satellites. The quality of this data bears great importance in achieving precise navigation outcomes, as the satellite coordinates are held constant in the data processing procedure.^3,15,16 In satellite navigation systems, broadcast coordinates information is essential for determining the position and velocity of GNSS satellites. Both ephemeris and almanac provide this information, along with satellite clock information such as offset, drift, and drift rate. The navigation message format and contents are specified in interface control documents (ICD), which also provide instructions for the use of this information. However, different constellations may use different reference systems and physical constants, and these differences can have an impact on position accuracy. Although the differences between the latest reference system realizations are generally negligible compared to broadcast ephemeris precision, physical constants such as Earth's gravitational coefficient (GM) must be used as defined by the ICD to avoid linearly growing position errors over time. Table 1 from Hugentobler and Montenbruck¹⁵ presents the values for GM and Earth rotation velocity (ωe) for various GNSS systems.

Ephemeris models

In the context of satellite navigation systems, the user receiver is responsible for computing the coordinates of the GNSS satellites by utilizing the information broadcast in the navigation messages. The approach adopted for accounting satellite orbit perturbations differs between GPS/Galileo/BeiDou and GLONASS systems, which consequently results in different contents of their navigation messages. The GNSS satellites, namely GPS, Galileo, and BeiDou, follow a Keplerian orbit in the first approximation, where perturbations are considered as temporal variations in the orbital elements. In contrast, the GLONASS satellite system broadcasts initial cartesian coordinates of position and velocity, along with the vector components of moon and solar gravitational acceleration perturbations, as part of their navigation message.

$\frac{d}{dt}\left(\begin{array}{c}r\\ v\end{array}\right)= \left(\begin{array}{c}v\\ a\end{array}\right).$   (1)

In accordance with the guidelines outlined in the GLONASS ICD document, the computation of GLONASS satellite coordinates is mandated. Table 2, as presented in Hugentobler and Montenbruck's¹⁵ work, provides a detailed list of the elements that are included in the satellite's navigation message. GLONASS utilizes the PZ-90 coordinate system to broadcast the initial position and velocity of the satellites through the navigation message. This message comprises x, y, and z coordinates along with corresponding velocities Vx, Vy, and Vz. In addition, it contains acceleration components Ax, Ay, and Az, which are the luni-solar acceleration projections on the axes of the ECEF Greenwich coordinate system. The gravitational forces of the moon and sun acting on the GLONASS satellites are the cause of these accelerations. Moreover, the GLONASS ephemeris involves a clock correction for a first-order polynomial. The clock offset is represented by TauM, whereas GammaN denotes the relative frequency offset.

In the context of computing GLONASS satellite coordinates, the initial conditions that are conveyed in the navigation message are expressed in the Earth-centered, Earth-fixed (ECEF) Greenwich coordinate system PZ-90. To properly integrate these coordinates, they must first be transformed to an absolute, or inertial, coordinate system at a specified epoch te (time of ephemeris), using the transformations specified in the GLONASS Interface Control Document (ICD) (GLONASS ICD, 2016). The acceleration components (Ax, Ay, and Az) represent the projections of lunisolar acceleration onto the axes of the ECEF Greenwich coordinate system. These accelerations must also be transformed into the inertial system to properly account for their effects. To avoid the need for explicit reference system transformations, the equation of motion is formulated in the rotating, Earth-fixed reference frame, incorporating centrifugal and Coriolis terms in the modeled acceleration (as shown in Equation 12).¹⁵

$\left(\begin{array}{c}{A}_x\\ A_y\\ A_z\end{array}\right)= -GM\overrightarrow{\frac{r}{r^3}}-\frac{\frac{3}{2}{J}_{2}GMa}{r^5}\left(\begin{array}{c}x\\ y\\ z\end{array}\right)\left(\begin{array}{c}\frac{x-5x{z}^2}{r^2} \\ \frac{y-5y{z}^2}{r^2}\\ \frac{3z-5z^3}{r^2}\end{array}\right)+ {\omega }^2\left(\begin{array}{c}x\\ y\\ 0\end{array}\right)+ 2\omega \left(\begin{array}{c}+Vy\\ -Vx\\ 0\end{array}\right),$   (2)

In Eq. 2, a is the semi-major (equatorial) axis of the PZ-90 Earth’s ellipsoid equals to 6378136 m, and J2 is the second degree zonal coefficient of normal potential equals to 1082625.75 106. The initial conditions for simplified algorithm integration are the coordinates $x=x\left(tb\right),y=y\left(tb\right),z=z\left(tb\right)$ , velocity vector components $Vx=Vx\left(tb\right),Vy=Vy\left(tb\right),$ and $Vz=Vz\left(tb\right)$ and perturbing accelerations Ax, Ay and Az for the SV’s center of mass at the instant tb is transmitted within navigation message data. Perturbing accelerations are considered constants at an interval of tb ±15 min. Numeric integration can be executed using for example the Runge-Kutta fourth-order method.¹⁷

Runge-kutta method

Runge-Kutta is a numerical technique used to solve an ordinary differential equation. Starting from initial values y0 in a time t0 a simple approximation can be calculated for y in a later time t0+h using a first-order Taylor expansion:

$y\left(t_0+h\right)\approx y_0+h{\dot{y}}_0=y_0+hf\left(t_0,y_0\right).$   (3)

Being this referred to as an Euler Step. From an initial point (t0, y0) and moving with a time-step of h along the tangent to the graph of y (Figure 2). Following this, it is possible to obtain approximate values η1 of the solution at distinct times.¹⁷

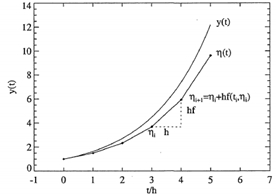
Figure 2 Approximation solution of a differential equation using Euler steps of size h.
Source: Montenbruck, Gill.¹⁷

The step size needs to be carefully chosen so the values will follow the curve over several steps and a better approximation. The general notation is given by:

$y\left(t_{{}_0}+h\right)\approx y_{{}_0}+h\Phi =\eta \left(t_0+h\right).$   (4)

For the approximate solution $\eta \left(t_0+h\right),$ the increment function $\text{(Φ})$ must closely approximate the slope of the secant through $(t_0,y_0)$ and $(t_0+h,y_0\left(t_0+h\right))$ which may not follow the slope of the tanged used in the Euler step. This problem was solved by Carl Runge and Wilheim Kutta which considers slopes at multiple points inside the integration step. In the 4th order Runge-Kutta, the increment function is calculated as the weighted mean is:

${\Phi }_{RK4}=\frac{1}{6}\left(k_1+2k_2+2k_3+k_4\right),$   (5)

and the four slopes are given as:

$k_1=f\left(t_0,y_0\right),$   (6)

$k_2=f\left(t_0+\frac{h}{2},y_0+\frac{h{k}_1}{2}\right),$   (7)

$k_3=f\left(t_0+\frac{h}{2},y_0+\frac{h{k}_2}{2}\right),$   (8)

$k_4=f\left(t_0+h ,y_0+h{k}_3\right).$   (9)

This formula is used to approximate the solution up to terms of order h4, if y(t) is sufficiently smooth and differentiable. Its local truncation error is secured by a term of order h5 (equations 19).¹⁷

$e_{RK4}= \left|y\left(t_0+h\right)-\eta \left(t_0+h\right) \right|\le h^5$   (10)

Equations to obtain satellite coordinates from the Caterian broadcast ephemeris

This section presents the equations needed for the implementation of the Runge-Kutta method. Following 6 first-order differential equations are needed to compute the satellite positions at any time:

$\frac{dx}{dt}= v_x\left(t\right)$   (11)

$\frac{dy}{dt}= v_y\left(t\right)$   (12)

$\frac{dz}{dt}= v_z\left(t\right)$   (13)

$\frac{d{v}_x}{dt}= -\frac{\mu x}{r^3}+\frac{3}{2}{C}_{20 }\frac{\mu a_e^{2}x}{r^5}\left(1-\frac{5z^2}{r^2}\right)+ w_e^{2}x+2w_e\frac{dy}{dt}+ \ddot{x}$   (14)

$\frac{d{v}_y}{dt}= -\frac{\mu y}{r^3}+\frac{3}{2}{C}_{20 }\frac{\mu a_e^{2}y}{r^5}\left(1-\frac{5z^2}{r^2}\right)+ w_e^{2}y+2w_e\frac{dx}{dt}+ \ddot{y}$   (15)

$\frac{d{v}_z}{dt} = -\frac{\mu z}{r^3}+\frac{3}{2}{C}_{20 }\frac{\mu a_e^{2}z}{r^5}\left(3-\frac{5z^2}{r^2}\right)+ \ddot{z}$   (16)

Detailed algorithm implementation steps in Python 3 and the library to perform these calculations can be found in https://github.com/loram93/GLONASS_PAPER. The repository contains the main file, the library, and files for day 100 from 2020 as an example of naming and data structure. The first values (w10, w20, w30, w40, w50, and w60) are obtained from ephemeris considering Earth rotation during the time of signal travel from the satellite to the user. For each time interval, that will be determined (i.e. 1ms, 10ms, 1 sec, etc.), between desired time and tb.

It was processed three days of data on 2020 (DOY 100 to 103) varying the steps from 0.01 up to 120 seconds. The computed used was a laptop Dell Inspiron 15 7000 series with an Intel I5 processor and 4GB of RAM. From the daily navigation message files, the coordinates were obtained to match the final products timesteps (15 minutes). The ECEF (Earth-Centered, Earth-Fixed) estimated and final coordinates were transformed into a local reference frame according to the equation in Montenbruck et al.,¹⁸ For GLONASS, according to the ICD documentation, it is not necessary to move the coordinates from the Center of Mass (CoM) to the Center of Phase (CoP) as the coordinates acquired from the navigation message are already located on the CoM. Figure 3 shows the coordinates on ECEF for R01.

Figure 3 R01 coordinates for DOY 100, 101, and 102.

Broadcast ephemerides

GLONASS broadcast navigation message data are publicly available at International GNSS Service (IGS) through the MGEX (Multi-GNSS Experiment). The MGEX multi-GNSS broadcast ephemerides product has been generated by Technische Universita¨t München (TUM) and DLR in a joint effort since 1 January 2013. Real-time streams of currently 38 selected MGEX stations to provide the basis for the generation of daily files with the prefix brdm. In the beginning, only GPS, GLONASS, and QZSS were covered. Subsequently, additional GNSSs were included: BeiDou since 11 February 2013, SBAS since 3 March 2013, Galileo since 12 March 2013, and IRNSS since 1 January 2016.¹⁹

In addition to the broadcast ephemeris files discussed so far, BKG provides a variety of real-time streams with multi-GNSS BCEs at their Ntrip caster. These comprise distinct streams for each constellation as well as a combined stream with GPS, GLONASS, Galileo, BeiDou, QZSS, and SBAS ephemerides. The BKG ephemeris streams provide complete and timely orbit and clock information for all GNSS satellites in a standardized message format and can serve a variety of applications from real-time positioning services to assisted GNSS.

Precise ephemeris

Currently, six Analise Centers (ACs) generate different sets of final orbits for MGEX:

1. Centre National d’Etudes Spatiales (CNES), Collecte Localisation Satellites (CLS), Groupe de
2. Recherche de Géodésie Spatiale (GRGS)
3. Center for Orbit Determination in Europe (CODE)
4. GeoForschungsZentrum Potsdam (GFZ)
5. Information and Analysis Center (IAC)
6. Shanghai Observatory (SHAO)
7. Wuhan University

First orbit and clock products for selected new constellations were provided by the MGEX Analysis Centers (ACs) in 2012 (GPS week 1680). Since then, an increasing number of multi-constellation products covering up to five global or regional navigation satellite systems have become available.

The outcomes of the analysis period for PR01 in terms of the radial, along-track, cross-track, and three-dimensional parameters are presented in Figure 4. The increments considered for the analysis were 1, 2, 10, 30, 45, 60, and 120 seconds. A comparative evaluation of the outcomes reveals that the increments larger than 1 second tend to manifest higher residuals, primarily in the radial component.

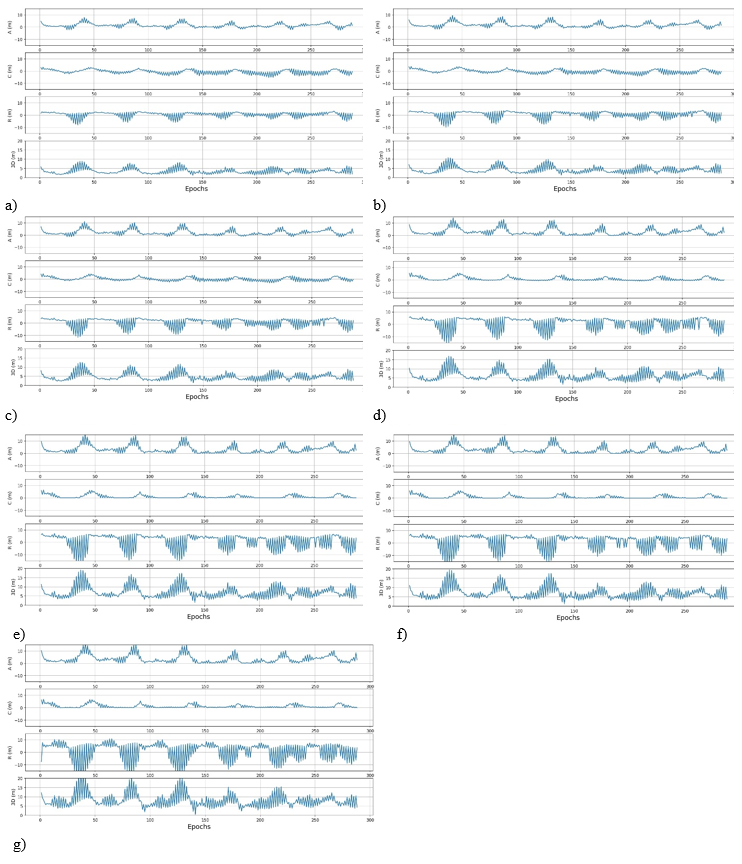
Figure 4 Residuals for R01 on the local components (along-track, cross-track and radial) and on the three dimensional. (a) 1 second (b) 2 seconds (c) 10 seconds (d) 30 seconds (e) 45 seconds (f) 60 seconds (g) 120 seconds time step.

The graphics also shows a zig-zag pattern where the residuals for the epochs closer to tb (time of reference) are smaller than the ones on the boundaries of the period (+/- 15 minutes). This happens due to the degradation of the cartesian elements transmitted to the satellites used in the integration process.

To understand how much the time step may degrade the accuracy of ephemeris the three days were processed, and all available, healthy satellites were considered. The time steps were 0.1, 1, 5, 10, 30, 45, 60, and 120 seconds. Considering all the available epochs it was calculated the RMSE (Root-Mean Square Error) which is used as a measure of the differences between values predicted, coordinates from the broadcast message, and the reference value; the precise coordinates from IGS. For the formulation (equation 17)is the reference observation,the estimated value and N the total number of observations.

$RMSE=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^N{\left(x_i-{\widehat{x}}_i\right)}^2}{N}}$   (17)

The results are presented in Figure 5. 24 satellites are part of these results. For 0.1 and 1 second the results are quite similar indicating that decreasing the step size to values under 1 second will not deliver any significant improvement on the accuracy. For values above 2 seconds, the integration process starts losing accuracy. Steps over 10 seconds will have 3D RMSE larger than 6 meters, which is not expected according to the ICD.

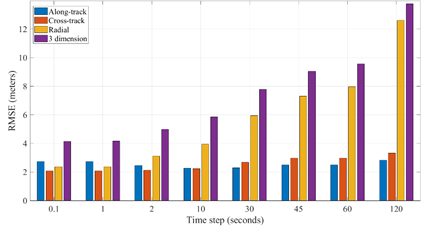
Figure 5 RMSE results for GLONASS satellites for three days (DOYS 100, 101, and 102 for the year 2020) varying the step size.

According to the results, to get the best accuracy possible on the integration process, a step size smaller than 1 second should be used. Figure 6 shows how decreasing this value may impact the processing time, due to the fact that a four-order interpolation process, such as Runge-Kutta, may be computational expeditious. The graph shows that a change between 1 to 0.1 seconds may increase the time of processing 6 times without any improvement on the accuracy of the coordinates acquired.

Figure 6 Elapsed time for the data processing presented in Figure 5 in minutes.

GLONASS broadcast ephemerides are transmitted in a different format when compared to other GNSS constellations. They are provided as satellite state vectors in cartesian elements and are updated every 30 min and must be numerically integrated to give satellite positions. In this paper it was presented the influence of the step size in the Runge-Kutta 4th interpolation on the accuracy and the computational time of processing. Stewart and Tsakiri⁷ showed initial results about GLONASS broadcast coordinates computation and recommended values of up to 30 seconds according to the available satellites and accuracy at the time. Since then, no other studies have been conducted about this topic and no study was found where the time span to calculate the coordinated were analyzed, which is of great importance for real-time applications. The fourth order Runge-Kutta method of numerical integration includes approximations and adds further errors to GLONASS satellite coordinates calculation. Choice of integration step length should be as short as possible to minimize integration errors but long enough to reduce the processing time span. Figure 4 presents the difference between the calculated coordinates and final products for satellite R01 for steps starting with 1 s. It is possible to observe that as the step increases the residuals will also increase significantly. From the tree components, the radial is the most affected and will directly influence the final accuracy. A full system assessment was made considering the healthy satellites that weren’t considered as a fault.²⁰ A total of 22 satellites were analyzed with 6336 epochs with steps sizes of 0.1s, 1s, 5s, 10s, 30s, 45s, 60s, and 120s.

Figure 5 shows the RMSE on the local coordinates and three-dimensional component. One can conclude that values smaller than 1 second does not improve the accuracy of the interpolation and any value larger than 30 seconds returns values with more than 7m, given as expected by the GLONASS ICD.⁶ Following the values in Figures 5&6 presents the time span to conduct the interpolation. Values smaller than 1s will keep the same accuracy, however, it will greatly increase the time of processing. For 0.1s the time of processing will increase 6 times and no gain in accuracy was found. Meanwhile, for 2 seconds the time decreased but the 3D RMSE increased from 4.14 to 4.98 m. So, a time step of 1sec appears to be a compromise between good accuracy and time span.

A functional library in Python 3 was made available. It is composed of main scrip that calls the libraries. It is important to notice that even though the highest accuracy is obtained with a 1-second time-step interpolation, the final RMSE of 4.14 meters in the tree-dimension element agrees with previous research that used a 1 second time step to address the accuracy of GLONASS ephemeris.^2,12 However Statella et al.,¹¹ achieved an accuracy of 6.53 m which gives a 2.39 m of difference. And comparing with other GNSS such as Galileo and GPS,^21,22 such value is considerable larger and the integration between systems should be carefully carried out due the impact of the coordinates of the satellite accuracy on the user range error (URE) for point positioning.

We acknowledge MGEX for providing the daily broadcast data, the National Institute of Science and Technology for GNSS in Support of Air Navigation (INCT GNSS-NavAer), funded by CNPq (465648/2014-2), FAPESP (2017/50115-0) and CAPES (88887.482174/2020-00). The libraries implemented in this research were developed in python 3 and are available at: https://github.com/loram93/GLONASS_PAPER .

The author declares that there is no conflict of interest.

1. Jerez, GO, Prudente P, Barroca D, et al. Theoretical review and state of the art. 2018;6(2):155–173.
2. Son E, Lim DW, Ahn J, et al. Comparison of Numerical Orbit Integration between Runge-Kutta and Adams-Bash forth-Moulton using Global Navigation Satellite System Broadcast Ephemeris. 2019;8(4):201–208.
3. Monico JFG. Posicionamento pelo GNSS. 2nd ed. São Paulo: Editora Unesp; 2008.
4. Jerez G. Analysis of GPS/GLONASS Integration for Positioning Under Ionospheric Scintillation Effect. Universidade Estadual Paulista Júlio De Mesquita Filho; 2017.
5. Revnivykh S, Bolkunov A, Serdyukov A, et al. Springer Handbook of Global Navigation Satellite Systems. In: Teunissen PJG, Montenbruck O, editors. 1st ed. Springer; 2017. p. 219–245.
6. Russian Space Systems, GLONASS Interface Control Document, General Description of Code Division Multiple Access Signal System. Russian Space Systems. JSC.
7. Stewart M, Tsakiri M. GLONASS Broadcast Orbit Computation. GPS Solutions.1998;2(2):16–27.
8. Chao CC, Gick RA. Long-term evolution of navigation satellite orbits: GPS/GLONASS/GALILEO. Adv Space Res. 2004;34(5):1221–1226.
9. Cai C, Gao Y. A combined GPS/GLONASS navigation algorithm for use with limited satellite visibility. J Navigation. 2009;62(4):671–685.
10. Wang J. An approach to GLONASS ambiguity resolution. J Geodesy. 2000;74(5):421–430.
11. Statella T, Aguiar CR, Monico J FG, et al. Calculation of the position and velocity vectors of the GLONASS satellites from the transmitted ephemeris and aspects related to their integration with the GPS. 2013;40(2):1–7.
12. Maciuk, K. Different approaches in GLONASS orbit computation from broadcast ephemeris. Geodetski vestnik. 2016;60(3).
13. Zhang C, Qianxin W, Yamin D, et al. Analysis and Modeling of GLONASS Broadcast Ephemeris Errors. In: Sun J, Liu J, Yang Y, Fan S, editors. China Satellite Navigation Conference (CSNC) Proceedings. 2012. p. 455–462.
14. Heng L. Safe satellite navigation with multiple constellations: Global Monitoring of GPS and GLONASS Signal-in-Space Anomalies. 2012.
15. Hugentobler U, Montenbruck O. Satellite Orbits and Attitude. In: Teunissen PJG, Montenbruck O, editors. Springer Handbook of Global Navigation Satellite Systems; 2017. p. 59–90.
16. Seeber G. Satellite geodesy : foundations, methods, and applications. New York: Walter de gruyter; 2003.
17. Montenbruck O, Gill E. Satellite Orbits. Berlin, Heidelberg: Springer; 2000.
18. Montenbruck O, Schmid R, Mercier F, et al. GNSS satellite geometry and attitude models. Adv Space Res. 2015;56:1015–1029.
19. Montenbruck O, Steigenberger P, Prange L, et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS) – Achievements, prospects and challenges. Adv Space Res. 2017;59(7):1671–1697.
20. Gunning K, Walter T, Enge P. Characterization of GLONASS broadcast clock and ephemeris: Nominal performance and fault trends for ARAIM. Proceedings of the 2017 International Technical Meeting of the Institute of Navigation; 2017. p. 170–183.
21. Alonso M T, Sanz J, Juan J M, et al. Galileo broadcast ephemeris and clock errors analysis: 1 January 2017 to 31 July 2020. Sensors. 2020;20(23):1–34.
22. Heng L, Gao GX, Walter T, et al. GPS ephemeris error screening and results for 2006-2009. Institute of Navigation - International Technical Meeting. 2010; 2010;2:1184–1192.