Launching a space probe from an orbiting platform into a resonant orbit is discussed and illustrated by convincing computer simulations. The probe is to approach the surface of the planet in order to explore it from a low altitude, or investigate far off space regions from an orbit with a high apogee. After the mission is fulfilled, the probe is to return to the orbital station and softly dock to it. Simple quantitative analysis of required maneuvers is based in the paper on fundamental laws of physics, the principles of energy and angular momentum conservation, and on Kepler’s laws. Considered examples of probe’s motions are illustrated by an accompanying simulation program. Material is appropriate for specialists in astrodynamics and orbital mechanics, as well as for a wide readership including astronautical engineers and other personnel involved or interested in space exploration.

Keywords: space exploration, astrodynamics, resonant orbits, period of revolution, impulsive maneuvers, soft docking

In this paper we present a simple treatment in terms of physics of trajectories suitable for a space probe, which is an automatic or manned module with scientific instruments launched from a station circularly orbiting the Earth or some other planet. The module is to approach the surface of the planet in order to explore it or to perform more detailed imaging of a planet’s surface from a low altitude. Then the module, with the scientific information it has collected, is to return to the orbital station and gently dock to it. Or, as another assignment, the space probe is to investigate far off space regions. In either case, its orbit must satisfy special requirements so that a rendezvous of the probe with the station be possible after the probe has completed its mission. Our aim is to show with the help of rather modest mathematical means that orbits suitable for space probes are actually possible, and how such orbits can be realized. Examples of probe’s motions relative to the planet and relative to the host orbital station are illustrated by a simulation program accompanying the paper.

Various problems related to orbital mechanics and astrodynamics similar to the above mentioned are discussed in many texts and papers.^1–5 Many useful references can be found on the web.⁶ Most of the papers on the subject are advanced texts written for experts and specialists. In this paper we use a rather simple approach accessible to non-experts and novices in astrodynamics. Our treatment of the problem is based on the fundamental laws of physics, on principles of energy and angular momentum conservation, and on Kepler’s laws. We have already used similar physically meaningful approach in a contribution to the journal Advances in Space Research.⁷ The information included in the present paper and in the accompanying software is suitable for the space enthusiast who wants to learn more about the fascinating science of space exploration.

If the probe is to investigate the surface of the planet, its orbit must approach the planet as closely as possible. Consequently, the orbit must have a low perigee (periapsis, for investigating some other planet rather than the Earth), but must not intersect the surface of the planet (more precisely, the upper rarefied strata of the atmosphere). Moreover, as an obligatory requirement, the period of revolution along such an elliptical orbit must be related to the period of revolution of the host orbital station along its circular orbit in such a way that the probe and station periodically meet one another. Such a rendezvous can occur only at a common point of their orbits in case their periods of revolution are in the ratio of integers, preferably small. The orbits that satisfy this requirement are called resonant. For example, if the period of revolution of the probe is 2/3 the period of the station, the station completes two revolutions while the probe completes three. Thus the two meet at the common point of their orbits every two revolutions of the station after the departure of the probe.

To keep things simple, we assume that the initial and final orbits are in the same plane. Similar maneuvers are often used to move spacecraft from their initial parking orbits to their final mission orbits. In such problems of space dynamics, the relative motion of the orbiting bodies is important.⁸ We assume also that the host orbital station stays in a parking circular orbit around the planet. After the space probe is undocked from the station, it moves along almost the same circular orbit and with almost the same velocity as does the station. In order to launch the probe into a required orbit, we should impart to it some additional velocity (otherwise called the velocity change or characteristic velocity) with the help of, say, an on-board rocket engine. When the engine is very powerful and operates for a very short time (so short that the probe covers only a very small portion of its orbit during the thrust), the change in the orbital velocity of the spacecraft is essentially instantaneous. Most propulsion systems operate for only a short time compared to the orbital period, so that we can treat the maneuver as an impulsive change in velocity while the spatial position of the probe remains unchanged.

In this paper it is assumed that the change in velocity occurs instantly. After such a maneuver the probe continues its passive orbital motion along a new elliptical orbit. The parameters that characterize the new orbit depend on the initial conditions implied by momentary values of the radius vector and the velocity vector of the space probe at the end of the applied impulse. Further on in this paper we concentrate on elementary analytical calculations of the velocity change, which is to provide the requirements that the new orbit of the space probe must satisfy. The paper comes along with a highly interactive simulation program⁹ developed by the author. The simulation allows us to watch motions of both the probe and space station on the computer screen (and simultaneously the motion of the probe relative to the station in a separate window) in a time scale convenient for observation. The relative motion reveals many extraordinary features that are hard to reconcile with common sense and our everyday experience.

To properly understand the design of space probe’s missions, it is essential to understand the laws that govern the passive motion of a body in a central field of gravity. In the subsequent analysis of possible trajectories, we assume that passive motion of the probe obeys Kepler’s laws. Kepler’s laws hold strictly if the body moves under the sole force of a central field whose strength falls off as a square of distance from the center. Such is the Newtonian gravitational field created by a point mass, and by a spherically symmetric star or planet. The latter field outside the planet is just the same as if the entire planet’s mass were concentrated at its center. However, an Earth’s satellite or a space probe, besides the gravitational field of the Earth, is subjected also to gravitational pulls of the Sun, the Moon and other celestial bodies. Then we can ask a natural question: Why is it possible to apply Kepler’s laws to the motion of artificial satellites and space probes?

The point is that usually we describe the satellite’s motion in the frame of reference associated with the Earth (non-rotating geocentric frame). Because the gravitational pull of the Sun gives very nearly equal accelerations to the satellite and to the Earth itself, we can assume that in the non-inertial geocentric frame the satellite’s passive motion is governed solely by the Earth’s gravity. Such possibility to ignore the gravitational influence of other bodies in the planetocentric reference frame is justified in celestial mechanics by introducing the so-called sphere of gravitational influence of a planet with respect to the Sun.^1,4 For the Earth, this region extends to more than a hundred Earth’s radii. Therefore orbits of all probes discussed in this paper lie deeply inside the sphere of gravitational influence. In terms of physics the situation can be explained as follows: The Earth together with its artificial satellites is freely falling in the gravitational field created by the Sun, so that all the bodies on the Earth and in its close vicinity, including the satellites in low orbits, occur in the “state of weightlessness” with respect to the gravitational field of the Sun (and of all other nearby and far-off massive celestial bodies). In other words, for any earthly body its gravitational attraction to the Sun and the Moon is very nearly compensated by the pseudo force of inertia, which is caused by the acceleration of the Earth as a whole under the gravitation of the Sun and the Moon. Slightly non-uniform character of this gravitational field is responsible for tiny effects of differential gravitation, which are usually described as tidal forces. For satellites in low orbits tidal forces constitute only about 10-7 of the Earth’s gravity-they are about ten million times smaller than the weight. More details regarding tidal forces can be found, say, in Refs.^4,10

From the point of view of rocket fuel expenditures, the most efficient method of transition to a suitable orbit consists of imparting to the space probe an additional velocity, which is tangent to its initial circular orbit. When the thrust is tangential to velocity, the amount of work done by the rocket engine ceteris paribus is the greatest, and so is the change in energy and in the speed of the orbiting craft. Launching a space probe by a velocity change tangential to the orbit is similar to the so-called Hohmann’s transfer between circular orbits through a transitional semielliptical trajectory that grazes the inner orbit from the outside and the outer orbit from the inside. It is amazing that the idea was suggested by a German engineer Walter Hohmann in 1925, at those old times, many years before launching artificial satellites became technically possible. If the thrust is tangential to the orbital velocity, the new orbit of the probe lies in the same plane with the circular orbit of the station. When the additional velocity is directed opposite to the orbital velocity of the station, we get an inner elliptical orbit that grazes the circular orbit of the station only at the orbital position at which the rocket engine thrusts the probe backward. This point is the apogee of the orbit. Otherwise, if the additional velocity is directed forward along the orbital velocity of the station, the probe moves to an outer elliptical orbit. The point of the velocity change (the burnout point) is the perigee of the new orbit.

 For choosing a suitable resonant orbit of a space probe, the crucial issue is the period of revolution. The value of additional (characteristic) velocity that must be imparted to the space probe after it’s undocking from the station in order to transfer the probe to an elliptical orbit with the required period of revolution can be calculated with the help of Kepler’s laws and principles of energy conservation and angular momentum conservation. This is done, for example, in.⁴ To get the orbit with the given arbitrary period T, the space probe must have after the undocking from the host station and burnout the planetocentric velocity u₀ (directed tangentially to the circular velocity u_circ of the orbital station), whose magnitude is given by the following expression:

${\upsilon }_0={\upsilon }_{circ}\sqrt{2-{\left(\raisebox{1ex}{$T_0$}\!\left/ \!\raisebox{-1ex}{$T$}\right.\right)}^{2/3}}$    (1)

Here T₀ is the period of revolution of the orbital station. The required magnitude of the initial velocity u₀ of the probe after the burnout is expressed here in terms of the circular velocity u_circ for the given radius of the station’s orbit and the ratio of periods T₀/T. This makes Eq. (1) applicable for space probes launched from an orbital platform investigating not only the Earth, but also an arbitrary spherically symmetric planet.

Next we consider several possible inner resonant orbits suitable for the space probe that should approach the surface of the planet as close as possible. After performing its mission, the space probe encounters the orbital station each time the station completes a revolution in case the period T of the probe’s revolution equals T₀/n, where T₀ is the period of the station, and n is an integer. However, there is actually only one such possibility, namely, n=2. Indeed, elliptical orbits with periods that equal T₀/3, T₀/4, T₀/5, . . . do not exist. The reason is that the shortest possible period of revolution along an inner elliptical orbit corresponds to the degenerate ellipse with the minor axis of zero length (a straight-line ellipse with foci at the center of the planet and at the initial point, and with a major axis equal to the radius of the circular orbit of the station). According to Kepler’s third law, this minimal period equals (1/2)^3/2T₀≈0.35T₀, a value greater than T₀/3.

For the inner elliptical orbit with the period T=T₀/2, the perigee distance r_P equals 0:26 r_A, where r_A is the apogee distance that equals the radius r₀ of the circular orbit of the station. Hence, this rather exotic orbit can be realized only if the radius of the station’s circular orbit is at least four times the radius of the planet. The backward velocity change Δu needed to transfer the space probe to this orbit from the initial circular orbit equals approximately 0.36u_circ, that is, 36% of the circular velocity u_circ. Table 1 lists the values of the initial velocity u₀ of the space probe and the corresponding values of the velocity change Δu=u₀-u_circ for several inner elliptical orbits suitable for space probes. These velocities are expressed in units of the circular velocity u₀ of the orbital station for convenience of usage in the simulations.⁹ The values in Table 1 are calculated with the help of expressions whose derivation is given in.⁴ The perigee distance r_P=2a-r₀ for each of the orbits (in units of the radius r₀ of the station’s circular orbit) is also listed. The corresponding inner orbit is possible if this distance is greater than the radius R of the planet. The difference r_P-R is the shortest distance from the surface of the planet reached by the space probe.

The inner elliptical orbit of the space probe whose period T equals 1/2 of the station period T₀ is shown on the left-hand panel of Figure 1. In this case a backward characteristic velocity Δu₁ of approximately 0.358u_circ is required (see Table 1). At point A the space probe is undocked from the station, and the additional velocity Δu₁ is imparted to it by an on-board rocket engine. As a result, velocity of the probe is reduced from the circular velocity u_circ to the value u₀=0.642u_circ required for the apogee of the desired elliptical trajectory with the period T₀/2. During one revolution of the station along its circular orbit the probe covers the elliptical orbit twice.

The right-hand panel of Figure 1 shows a very counterintuitive trajectory of this space probe in the rotating non-inertial reference frame associated with the orbital station (more exactly, in the reference frame associated with the straight line joining the station and the center of the planet). In other words, this is the trajectory of the probe as it appears for the astronauts residing on the orbital station. The trajectories of the probe in the two frames of reference shown in Figure 1 (and in all subsequent figures of this paper) are generated with the help of the simulation program “Orbital Maneuvers and Relative Motion” that accompanies the paper. This program is a part of the award-winning software package “Planets and Satellites”.⁹ It is supplied with a detailed online Tutorial which describes the possibilities of the simulation program, and explains how to use it. We emphasize that the program does not use the analytical solution (which we have used above only for calculating the required velocity change of the probe): The program simply integrates numerically (using Runge–Kutta method of the 4th order) the differential equations of motion. The simulation allows us to watch on the computer screen the motion both of the orbital station and the space probe with respect to the planet, and to simultaneously watch the motion of the probe relative to the station. The motion is displayed in some time scale, which we can vary for convenient observation.

In order to use the program “Orbital Maneuvers and Relative Motion”⁹ for illustrating the maneuvers described in the paper, we can simply click the item “Examples” in the menu to open the list of predefined examples. Thus we can avoid calculations of necessary parameters for executing a desired simulation. We simply choose the relevant example in the list. A short description of the chosen example appears below in the text window. When we click “Ok” button, all the values required for the chosen simulation will be defined by the program and loaded automatically. Besides the maneuvers discussed in the paper, the set of predefined examples illustrates a lot of other various possible orbital missions. The program includes context-sensitive help and explanations, which are invoked from within the program by pressing F1 key or by clicking menu item “Help on Physics.” Relative to the orbital station, the probe after undocking first moves backward, in the direction of the additional velocity Δu₁ (see the right-hand panel of Figure 1), but soon the probe descends toward the planet and overtakes the station. When the probe passes through perigee P of its orbit for the first time, it occurs at point P of the trajectory that it traces relative to the station (see the right-hand panel of Figure 1) at the shortest distance from the surface of the planet. At the perigee P the distance r_P from the center of the planet equals approximately 0:26r_A, where r_A is the apogee distance (that equals the radius r₀ of the circular orbit of the station). Relevant calculations can be found, say, in.⁴ As we already mentioned, this means that such an orbit can be realized only if the radius of the initial circular orbit (orbit of the station) is at least four times the radius of the planet.

After passing through P, the distance to the planet increases and reaches its maximum value at the moment at which the probe passes again through the apogee A of its orbit. On the trajectory of the relative motion, this position of the probe is A′ (see the right hand panel of Figure 1). The station at this moment passes through the opposite point (with respect to the burnout point A) of its circular orbit. The probe occurs at the same minimal distance (point P′) for the second time during the second revolution along its elliptical orbit, and then meets the station at point A. To equalize its velocity with that of the station for the soft docking, another additional impulse Δu₂ is required. Its magnitude is the same as that of Δu₁, but its direction is opposite to Δu₁, because we must increase the velocity of the probe and make it equal to the velocity u_circ of the station. To observe the above-described counterintuitive simulation with the help of the package “Planets and Satellites”,⁹ we can simply choose “Inner Space Probe (Period T₀/2)” from the list of predefined examples in the program “Orbital Maneuvers and Relative Motion.”

The inner elliptical orbit of the space probe whose period equals 2/3 of the station’s period is shown on the left-hand panel of Figure 2. In this case a backward characteristic velocity Δʋ of approximately 0.17ʋ_circ (in magnitude) is required (see Table 1). At arbitrary point A the space probe is undocked from the station and the velocity change Δʋ is imparted to it by an on-board rocket engine. At the perigee P of the elliptical orbit the distance r_P from the center of the planet equals approximately 0.53r₀ (see Table 1). Hence, the orbit is suitable for a space probe if the circular orbit of the station has a radius approximately twice the radius of the planet.

The right-hand panel of Figure 2 shows the trajectory of this space probe in the rotating reference frame associated with the orbital station. For a while after the launch, the probe retrogrades in this frame in the direction of the velocity change Δu. However, soon its trajectory turns first toward the planet and then forward-the probe overtakes the station in its orbital motion. As a whole, the trajectory of the probe’s relative motion bends around the planet in the same sense as the orbit of the station, in spite of the retrograde direction of the additional velocity. Near the apexes of the loops of the trajectory the motion of the probe becomes retrograde. These apexes correspond to the instants at which the space probe passes through the apogee of its geocentric orbit. Passing once along this whole closed trajectory of the relative motion, the probe approaches the surface of the planet three times. At these moments the probe passes through the perigee of its geocentric orbit.

The simplest way of simulating the above-described motion with the help of the package “Planets and Satellites”⁹ is choosing “Space Probe with the Period 2T₀/3” in the list of predefined examples from within the program “Orbital Maneuvers and Relative Motion.” To dock the space probe softly to the station after the voyage, we should quench the remaining relative velocity (to equalize the geocentric velocities of the probe and the orbital station). This can be done by the same on-board rocket engine. The required additional impulse (the characteristic velocity of the maneuver) is just of the same magnitude as at the launch of the probe, but in the opposite direction: if at the launch the impulse is directed against the orbital velocity of the station, now at docking it should be directed forward.

Figure 3 illustrates the motion of a space probe with the period of revolution T=3/4T₀. In this case the probe meets the station at the initial point A after four revolutions around the planet. The station completes three revolutions during this time. The trajectory of motion of the probe relative to the orbital station has four loops that correspond to the time moments at which the probe passes through the apogee of its orbit. This simulation (as well as all other simulations considered below in this paper) can also be found in the list of predefined examples included in the program “Orbital Maneuvers and Relative Motion” of the package “Planets and Satellites”.⁹

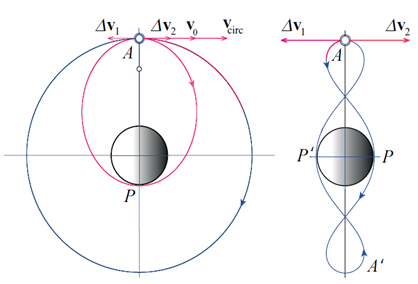
Figure 1 Elliptical planetocentric orbit of the space probe with the period 1/2T₀ (left) and the trajectory of the space probe in the reference frame associated with the orbital station (right).

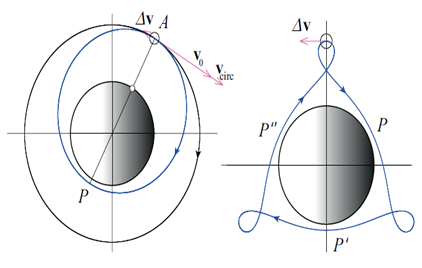
Figure 2 Elliptical orbit of the space probe with the period 2/3T₀ (left) and the trajectory of the space probe in the reference frame associated with the orbital station (right).

Figure 3 Elliptical orbit of the space probe with the period 3/4T₀ (left) and the trajectory of the space probe in the reference frame associated with the orbital station (right).

If the additional velocity imparted to the probe after its undocking from the station is directed forward, tangentially to the orbit of the station, the resulting elliptical orbit encloses (circumscribes) the circular orbit of the station. The initial point at which the orbits graze one another is the perigee of the elliptical orbit. Such outer orbits of space probes with suitable periods of revolution may be used to investigate the far-off space regions.

Table 2 lists the values of the initial velocity ʋ₀ of the space probe and the corresponding values of the velocity change Δu=u₀-ʋ_circ for several outer elliptical orbits of the probe. The apogee distance r_A=2a-r₀ for each of the orbits (the greatest distance of the probe from the center of the planet) is also listed. Figure 4 shows such outer elliptical orbits with the periods 3/2T₀ and 2T₀ (orbits 1 and 2, respectively). The right-hand panel of the figure shows the relative trajectories of the probe for these cases. At first the probe moves relative to the station in the direction of the initial velocity, but very soon its trajectory turns upward and then backward, and the motion becomes retrograde-the probe lags behind the station. In this frame, the trajectory of the space probe bends around the planet in the sense opposite to the orbital motion of the station.

For the orbit with the period T = 3/2T₀, the velocity change is approximately 0.11u_circ, and the distance to apogee A₁ (the greatest distance from the center of the planet) is 1.62 r₀ (r₀ is the radius of the circular orbit). The closed orbit of relative motion (curve 1 on the right-hand panel of Figure 4) has two small loops, corresponding to the time moments at which the probe passes through the perigee of its geocentric elliptical orbit. The whole closed path of the relative motion corresponds to two revolutions of the probe along the geocentric elliptical orbit, covered during three periods of revolution of the station. The trajectory with the period T=2T₀ (see Figure 4) requires the velocity change Δu directed forward, whose magnitude must be 0.17u_circ, (see Table 2). The distance r_A to apogee A₂ equals 2.17r₀. The closed orbit of the relative motion (curve 1 in Figure 4) is covered during 2T₀, that is, during two periods of revolution of the station.

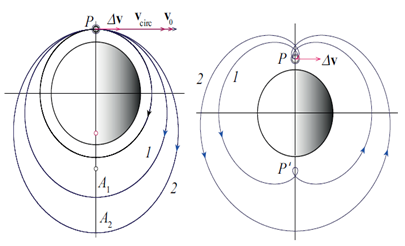
Figure 4 Elliptical planetocentric orbits of the space probes with the periods 3/2T₀ and 2T₀(trajectories 1 and 2 respectively, left panel), and the corresponding trajectories in the reference frame associated with the orbital station (right panel).

In order to investigate both the surface of the planet and remote space regions by the same space probe, we can use an elliptical orbit obtained by imparting to the probe a transverse additional impulse. If the additional velocity Δv is imparted to the probe in the radial direction (vertically up or down), the period of revolution is always greater than the period of the orbital station. An example of such an orbit with the period of revolution T=3/2T₀ is shown in Figure 5.

At point B of the initial circular orbit, the probe is undocked from the station, and the on-board rocket engine imparts a downward additional velocity Δu₁. The required magnitude of Δu₁ (the velocity change of the maneuver) can be calculated on the basis of Kepler’s laws and the principle of energy conservation. Applying to the case under consideration these fundamental laws of physics, and taking into account that a radial impulse of the rocket thrust does not change the angular momentum of the space probe, we obtain the following expressions for the distances of the apogee and perigee of the elliptical orbit from the center of the planet:

$r_A=\frac{r_0}{1-\raisebox{1ex}{$\Delta \upsilon $}\!\left/ \!\raisebox{-1ex}{${\upsilon }_{circ}$}\right.};r_P=\frac{r_0}{1+\raisebox{1ex}{$\Delta \upsilon $}\!\left/ \!\raisebox{-1ex}{${\upsilon }_{circ}$}\right.}$   (2)

Therefore, the semi-major axis of the elliptical orbit of the space probe depends on the magnitude Δu of the transverse velocity change as follows:

$a=\frac{1}{2}\left(r_A+r_P\right)=\frac{r_0}{1-{\left(\raisebox{1ex}{$\Delta \upsilon $}\!\left/ \!\raisebox{-1ex}{${\upsilon }_{circ}$}\right.\right)}^2}$    (3)

Suitable orbits for the space probe must have certain periods of revolution. We can use Kepler’s third law r₀/a=(T₀/T )^2/3 to calculate the velocity change Δu that gives an orbit with the required period of revolution T. With the help of Eq. (3), we obtain

$\left(\frac{\Delta v}{v_{circ}}\right)=\sqrt{1-{\left(\frac{T_0}{T}\right)}^{2/3}}$    (4)

For example, to obtain the orbit of the space probe with a period that is one-and-a-half periods of the orbital station (T₀/T=2/3), the required velocity change Δv calculated from Eq. (4) is 0.487u_circ. The probe returns to the station after every two revolutions in its elliptical orbit. During this time the station makes three full revolutions in its circular orbit, and they meet at the initial point B. Such resonant elliptical orbit is shown in Fig. 5. To obtain the orbit with the period T = 3/2T₀, a rather large characteristic velocity of 0.487u_circ is necessary. This value is several times larger than the tangential velocity change of 0.11u_circ needed for the elliptical orbit of the same period and the same major axis. To explain with the laws of physics why an azimuthal impulse is so much more effective than a radial one for achieving the elliptical orbit of the same energy (and hence of the same period of revolution), we should take into account that when the thrust is aligned with velocity, the amount of work done by the rocket engine is the greatest, and so is the change in energy of the orbiting craft.

To dock softly the space probe to the station, another additional impulse from the rocket engine is required. To equalize the orbital velocities, an additional velocity of the same magnitude as at the launch must be imparted to the space probe, but now it should be directed radially upward (Δu₂=-Δu₁, see Figure 5). The relative motion of the space probe in this case is shown on the right-hand panel of Figure 5. In the reference frame associated with the station, the space probe covers its convoluted closed path during three revolutions of the station around the planet. For T₀/T=4/5 Eq. (4) gives Δu/u_circ=0.372. In this case the space probe and the station meet after every four revolutions of the probe and five revolutions of the orbital station.

Figure 5 Elliptical orbit of a space probe with the period 3/2T₀ (left) and the corresponding trajectory in the reference frame associated with the orbital station (right) in the case of a transverse additional impulse.

It is possible to launch a probe that will return to the host station after one revolution of the station. The period of revolution T of such a probe in its elliptical orbit must be the same as the period T₀ of the station. In accordance with the 3rd Kepler’s law, the major axis of this ellipse must be equal to the diameter of the circular orbit of the station. This means that immediately after the launch the probe’s velocity u₀ must have the same magnitude u_circ as that of the station: u₀=u_circ. In other words, the velocity vector of the probe must turn after the rocket thrust through some angle preserving its magnitude (see Figure 6 for the case α=30◦).

For the desired given value of the angle, the required velocity change can be calculated as follows:

$\Delta \upsilon =2{\upsilon }_{circ}\sin \left(\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)$    (5)

Direction of the additional velocity vector Δu must make the angle α=2 (backward) with the downward vertical (see Figure 6). We note some geometrical properties of the probe’s elliptical orbit. Its major axis is parallel to the vector u₀ of the probe’s initial velocity. The distance between the foci of the ellipse equals 2r₀sinα. Hence the perigee distance r_P from the center of the Earth equals r₀(1-sinα), the apogee distance r_A equals r₀(1+sinα). For the case α=30◦ shown in Figure 6, r_P=r₀=2 and r_A=3r₀/2. The closed trajectory traced by the space probe relative to the orbital station is rather counterintuitive (right panel of Figure 7). This relative motion can be observed with the help of the simulation program.⁹ The velocity change Δu required for the maneuver that provides a certain value of the angle can be obtained in the simulation by two consecutive rocket thrusts. First, a backward instantaneous impulse Δu₁ is imparted to the probe, and immediately after it the second impulse Δu₂ is imparted vertically downward. Resulting velocity change Δu=Δu₁+Δu₂ must be equal to ʋ_circ in magnitude and directed at the angle α=2 (backward) with respect to the downward vertical. It follows from this requirement that the magnitudes of Δu₁ and Δu₂ must have the following values:

$\Delta {\upsilon }_1=2{\upsilon }_{circ}{\sin }^2\left(\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right),\Delta {\upsilon }_2=2{\upsilon }_{circ}\sin \left(\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)\cos \left(\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)={\upsilon }_{circ}\sin \left(\alpha \right)$  (6)

The probe and the station meet after one revolution of each along their orbits. To equalize their velocities for soft docking, the velocity change of the same magnitude Δu=2u_circsin(α=2) is required, so that the whole Δu-budget for the space probe mission is twice as great.

Figure 6 Circular orbit of the station and elliptical orbit of a space probe with the period T=T₀. Small circles on the trajectories show simultaneous positions of the orbital station and the probe.

Figure 7 Elliptical orbit of a space probe with the period T=T₀ (left) and the corresponding trajectory in the reference frame associated with the orbital station (right).

Next we consider one more example of space maneuvers. Imagine we need to launch a space vehicle from the orbital station into the same circular orbit as that of the station, but there is to be an angular distance of 180◦ between the vehicle and the station. This mission can provide a possibility of simultaneously watching the whole surface of the planet (both hemispheres) from the station and from the probe. In other words, they are to orbit in the same circle but at opposite ends of its diameter. This goal cannot be achieved by a single maneuver. The on-board rocket engine must be used at least twice. With two impulses we can transfer the space vehicle to the opposite point of the circular orbit using an intermediate elliptical orbit with the period of revolution, say, 3/2T₀ or 3/4T₀. In the first case, after undocking from the station, an additional velocity Δu₁ is imparted to the space vehicle in the direction of the orbital motion (see Figure 8). To calculate the required value of the velocity change magnitude Δu₁ for the maneuver, we can use again the conservation laws of energy and angular momentum, and Kepler’s third law. If the period T for the outer elliptical orbit must equal 3/2T₀, initial velocity ʋ₀ of the probe at the perigee P, according to Eq. (1), must have the magnitude of $\sqrt{2-{\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\right)}^{2/3}}$ u_circ=1.1121u_circ, whence Δu₁=0.1121u_circ.

During one revolution of the space vehicle along its elliptical orbit (see Figure 8), the station covers exactly one and a half of its circular orbit. That is, the space vehicle reaches the common point P of the two orbits (circular and elliptical) just at the moment when the station is at the diametrically opposite point of the circular orbit.

In the relative motion, shown on the right-hand panel of Figure 8, the space vehicle has covered one half of its closed path. At this moment, the excess of velocity of the space vehicle over the value u_circ is quenched by a second jet impulse, and the vehicle moves along the same circular orbit as the station but at the opposite side of the orbit. In the window of the simulation program⁹ that displays the relative motion, the space vehicle is stationary at the antipodal point. Clearly the second jet impulse must be of the same magnitude as the first one but opposite to the orbital velocity (Δu₂=-Δu₁, see Figure 8). We leave to the readers to consider and simulate on their own (with the help of the program⁹) the second above-mentioned possibility of transition to the opposite side of the same circular orbit with the help of an inner intermediate elliptical orbit, for which the period of revolution equals 3/4T₀. The required value of the vehicle’s initial velocity must be equal to $\sqrt{2-{\left(\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\right)}^{2/3}}$ u_circ=0.8880u_circ, whence the backward velocity change Δu=0.1120ʋ_circ. It occurs that both possibilities of transitions (through these outer and inner elliptical orbits) require almost the same relative magnitude of the velocity change (0.1120 versus 0.1121).

Figure 8 Transition of the space probe to the opposite point of the circular orbit. An elliptical orbit with the period 3/2T₀ is used (left panel). The trajectory in the reference frame associated with the orbital station is shown on the right panel.

Many important problems in astrodynamics are associated with modifying the orbit of a satellite or a spacecraft in order to produce a particular trajectory for an intended space mission. To plan such space flights, we must solve various problems related to the design of suitable transitional orbits. In unusual conditions of the orbital flight, navigation is quite different from what we are used to on the Earth’s surface or even in the air or under the water, and our intuition fails us. The orbital maneuvers are not as simple as driving a car or a motor boat or even flying a plane from one point to another. In this paper we have shown how the fundamental laws of energy and angular momentum conservation can be used for analytical calculations of the required velocity change for the desired maneuver of the spacecraft. The interactive simulation experiments⁹ reveal many interesting peculiarities of the orbital motions, and enhance understanding by complementing the analytical study of the subject in a manner that is mutually reinforcing.

To provide a possibility of the space probe’s subsequent rendezvous with the station at a common point of their orbits, the velocity change of the probe must satisfy the requirement that the period of revolution of the space probe along its elliptical orbit relates to the period of revolution of the orbital station along its circular orbit as a ratio of integers. The velocity change of the probe required for a specific mission can be calculated by rather modest mathematical means, without integrating the equations of motion. Trajectories of a space probe in the geocentric reference frame, and very counterintuitive trajectories of the probe’s relative motion in the reference frame associated with the orbital station, are illustrated by convincing computer simulations.⁹ Contemporary interactive media offer us a convenient means to visualize and to explore the orbital motions governed by the gravitational forces. The simulation program⁹ creates vivid and lasting impressions of the investigated phenomena, and provides us with a powerful tool to explore basic concepts that are difficult to understand in an abstract conventional manner.

None.

The author declares that there is no conflict of interest.

1. Bate RR, Mueller DD, White JE. Fundamentals of Astrodynamics. Newyork: Dover Publications Inc; 1971. 455 p.
2. Wiley Larson J, Wertz JR. Space Mission Analysis and Design. 2nd ed. California: Microcosm Inc; 1992. 504 p.
3. Vallado DA. Fundamentals of Astrodynamics and Applications. Newyork: McGraw-Hill Inc; 1997. 950 p.
4. Butikov EI. Motions of Celestial Bodies. Bristol: IOP Publishing Ltd; 2014.
5. Hintz GR. Orbital Mechanics and Astrodynamics-Techniques and Tools for Space Missions. Switzerland: Springer International Publishing; 2015. 386 p.
6. Braeunig RA. Rocket and Space Technology; 2015.
7. Butikov EI. Orbital Maneuvers and Space Rendezvous. Advances in Space Research. 2015;56(11):2582–2594.
8. Butikov EI. Relative Motion of Orbiting Bodies. Am J Phys. 2001;69:63–67.
9. Butikov EI. Planets and Satellites: computer simulations. Newyork: American Institute of Physics; 1999. 176 p.
10. Butikov EI. A Dynamical Picture of the Oceanic Tides. Am J Phys. 2002;70(10):1001–1011.