In aeronautical design activities it is necessary to have reasonable indications on the characteristic dimensions of typical defects that may occur in structures under load in order to indicate their correct hazard/risk level as a function of size and to allocate time/importance of any necessary corrective action. With reference to the behavior of the stiffened panels loaded in compression, which constitutes vast majority of thin-walled structures inside modern transport aircraft, it is of interest to evaluate when and under what conditions any skin-to-stringer de-bonding induces a local critical condition at a load lower than the global critical load related to the whole panel, compromising the theoretical bearing capacity of the panel itself. A simplified procedure is proposed to solve this problem, useful in the context of the preliminary aeronautical design stage: a defect size has been provided considering it as a significant dimension for the design and sizing of the structure. Dimensionless approach is also provided to allow extensive application of the procedure to several practical structural cases. The variation in damage size as a function of the geometrical parameters of the stiffened configuration and in function of the elastic modulus of the material constituting the panel itself is presented and investigated. The significant size tends to reduce if the stringer stiffness is higher than the skin one. This can be obtained both by means of geometrical parameters variation, as indicated, and by the introduction of a more performant stringer material at fixed geometry. The significant de-bonding dimension remains of the order of the stringer distance for practical application. The reported results allow a first approximate definition of design assumptions and maintenance indications. The generality of the presented approach makes it useful in evaluating all practical cases under similar operating conditions.

Keywords: damage-oriented evaluation, preliminary design of stiffened panels, skin-stringer de-bonding effect on global performance

The reduction of the aircraft weight increasing the related structural efficiency, addresses the design efforts towards structural configurations that are basically made by thin-walled and stiffened arrangements such as the well- known “reinforced shell construction”, remaining into the airworthiness regulation and ensuring both resistance and integrity. The stiffened panel configurations are therefore very common in practical applications both in homogeneous isotropic materials and in composite/hybrid configurations such as in the case of composite skin and isotropic stringer or vice versa. Compared to the simple shell configuration, it is possible to increase the applied load without failure inside the flight envelope with a limited added mass that remains consistent to aeronautical applications. The presence of thin-walled elements, however, introduces global and local critical phenomena that limit the maximum tolerable load also in function of the post-critical behavior that the panel assumes.^1-4 Considering the critical load associated with a specific configuration as a design limit, it remains necessary to understand which type of critical load must be considered in design among the global, torsional or induced by local phenomena. Usually in the design of the stiffened panel the global critical level is considered as a design data assuming that the other critical load levels can occur at higher load values. There is a wide literature that analyzes the critical conditions of stiffened panels and their post-critical behavior to evaluate the safe load-range useful for such structures [^5-9 as an example]: some specific conditions and design indication are determined.

The production of the stiffened panels can take place by riveted junctions, by gluing/bonding or through integrated production techniques based on the cost effectiveness evaluation associated with the structure.¹⁰ Production errors or anomalies induced by impact damage can introduce areas into the structure that are no longer compliant or no longer consistent with what was expected in the design calculations. The most common anomalies that occur in these configurations can be connected to de-bonding of a portion of the skin to the stringer interface due to lack of connections or loss of adhesion (de-bonding), breakage or damage of the elements of the stringer or breakage of the skin involving common stringer parts.^11-16 In the most common situation of skin-to-stringer de-bonding, an area of the structure is created where the structural behavior can be different with respect to what was initially expected. In fact, such damage modifies the compressive structure behavior by introducing a critical load level associated with the de-bonded skin portion. The global critical load can therefore be preceded by a local critical load with local post-critical behavior of the debonded plate which makes the structure no longer consistent with the criteria adopted in the design.^17-19 This behavior is strongly dependent on the relative stiffness of the part involved into the damaged configuration and damage size. From the design point of view, it becomes important to understand which de-bonded dimension is related to a significant reduction of the reference critical load and therefore of the strength of the structure. This different behavior is also linked to the definition of the corrective and maintenance actions to be envisaged in the event of such an anomaly that can be detected during periodic inspections. Identification of a maximum admissible damage size is essential for assessing the correct defect hazard situation and for assigning it to the correct maintenance procedure in order to maintain the level of structural integrity within the regulatory guidelines.

In the presence of fatigue loads, an unexpected evolution of this damage is likely to be evaluated on the basis of the operational load levels complicating any static analysis and design expectations.^14-16

The purpose of this technical note is to present a simplified procedure to be used in the preliminary design stage to find the characteristic length of a skin-to-stringer de-bonding in compressed flat stiffened panels. An isotropic five T-stiffener plate configuration is selected as an example for presenting the procedure. The difference in material is included into the derivation, taking into account separate elastic modules for the skin and the stringer respectively, as representative of hybrid or composite cases. The stiffened plate critical load has been determined according to the analysis of the repetitive element that is evaluated on the basis of the Eulerian critical load that generates an induced load on the de-bonded skin. Such a load has to be compared to the critical load of the debonded plate in order to evaluate its critical behavior or post-critical one. It is assumed that if the de-bonded portion of the panel has a critical load higher than the one pertaining to the global reference condition, then the de-bonding damage is considered not-effective for the purposes of the calculation. Otherwise, the de-bonding length is considered effective causing a deleterious influence to the load capacity of the reference stiffened panel. If the de-bonding length exceeds that limit, local buckling and lateral deflections are obtained and the local behavior of the skin can interfere with the compressive behavior of the stiffened panel. Furthermore, this local critical situation causes a redistribution of the load on the other elements of the panel, going toward a premature failure condition. In this local post-critical phase propagation phenomena are possible under fatigue load condition. A consequent evaluation of the growing properties of the damaged part becomes decisive for the duration estimate of the whole structure. This aspect is out of the scope of the present technical note but can be included is a subsequent analysis.

An excessive de-bonding length, about the order of or greater than half the length of the stiffener, can cause a more favorable local failure mode for the stringer that is no longer adequately supported by the rest of the structure, so such de-bonding dimension is not considered in the preliminary evaluation presented here.

The variability of the de-bonding limit for possible design considerations is therefore an expected result from this simplified procedure both based on the geometrical parameters of the stiffened configuration, and the characteristics of the materials used in its production. Conclusive design indications are expected for a correct identification of such damage type in aero-structural applications.

The reference configuration assumed for this investigation is presented in Figure 1. A T-stiffened flat panel with five stringers is taken into consideration for the analysis. The length L and width B are overall dimensions of the panel and the inter-stringer distance is assumed as “p”. The p dimension is also considered as the reference width of a repetitive element used into the procedure for the critical load definition. The repetitive element consists of a skin portion of width p including the relative stringer. Simply supported boundary conditions are considered for the loaded ends while free conditions are assumed for the lateral sides of the whole panel. This boundary conditions are representative for the analysis of the repetitive element critical load and behavior by means of the Eulerian compressed beam method. This condition is assumed consistent with the presented calculation within the limits of a preliminary design estimate of the critical situation.

Figure 1 Initial configuration with supported ends and free sides; configuration with de-bonding.

A skin-to-stringer de-bonding is assumed in the central position of the repetitive element to evaluate the possible local critical situation encountered by these configurations. The effect of de-bonding length has been investigated in order to evaluate its effect on the global critical behavior of the repetitive element and, as a consequence, the integrity status of the whole stiffened plate. Figure 2 presents the de-bonding portion of the skin assumed in a central position of the panel and crossing the reference stringer. This portion of the skin is evaluated with respect to its critical regime, that is related to the critical condition of the skin in the repetitive elements by means of defined formulas for critical load calculation of simply supported flat plate.^20,21 Two cases are studied such as: a) isotropic de-bonded plate and b) special orthotropic de-bonded plate. In Figure 3 the typical repetitive element is reported with several geometrical parameters. The compression load is applied along the direction of the stringer in such a way as to generate a local buckling of the skin in the de-bonding area with the evidence of the deformation mode under load in the local buckling conditions. The local buckling of the de-bonded skin part is the major effect of the considered phenomenon. The influence of such critical situation is dependent on the geometrical reported parameters, in particular the de-bonding length “d” and the considered materials. The definition of a significant de-bonding dimension is the result expected from this analysis obtaining a certain interest within a preliminary design phase in aircraft structures. The methodology follows the well-known Eulerian approximation of the critical compressive load applied to the repetitive element connected to the definition of the critical load of a simply supported plate, representative of the skin portion in the de-bonded area. The first part of the analysis provides a load level related to the skin corresponding to the critical condition of the repetitive element while the second calculation provides the critical load of the de-bonded plate. For this calculation a representative plate of width 2p and length d is considered.

Figure 2 Part of the panel affected by the damage (de-bonding) straddling the current (yellow).

Figure 3 Repetitive element with design parameters: a) section point of view; b) lateral point of view.

The Eulerian critical load of compressed simply supported column, related to the repetitive element, is reported as follows:

$N_{x-cr}=\frac{{\pi }^{2}EI}{p{l}^2}$

$\frac{EI}{p}=D_{CC}$

$N_{x-cr}=\frac{{\pi }^2}{l^2}{D}_{CC}$

The bending stiffness, the length of the column and the width p of the repetitive configuration are easy to be identified. As indicated previously the analysis is focused on structural configuration obtained by a skin and stringer made by different materials. For this reason, the global bending stiffness has to be determined with respect to the centroidal reference. The centroidal coordinate and position with respect to the reference system, as indicated in Figure 3, is defined as follows:

$y_c=\frac{t}{2}\frac{\left[-1+\frac{b}{p}\frac{s_1^2}{t^2}\frac{E_c}{E_p}+2\frac{h^2}{t^2}\frac{s_2}{p}\left(\frac{s_1}{h}+\frac{1}{2}\right)\frac{E_c}{E_p}\right]}{1+\frac{b{s}_1}{pt}\frac{E_c}{E_p}+\frac{h{s}_2}{pt}\frac{E_c}{E_p}}$

The centroidal position is reported as a function of several geometrical and material modulus ratio assumed for the skin and the stringer. The calculated bending stiffness is reported as follows:

$D_{CC}=\frac{t^3}{12}{E}_p\left[1+12{\left(\frac{1}{2}+\frac{y_G}{t}\right)}^2+\frac{b}{p}\frac{s_1^3}{t^3}\frac{E_c}{E_p}+12\frac{b}{p}\frac{s_1^3}{t^3}{\left(\frac{1}{2}-\frac{y_G}{s_1}\right)}^2\frac{E_c}{E_p}+\frac{h^3}{t^3}\frac{s_2}{p}\frac{E_c}{E_p}+12\frac{h^3}{t^3}\frac{s_2}{p}{\left(\frac{s_1}{h}+\frac{1}{2}-\frac{y_G}{h}\right)}^2\frac{E_c}{E_p}\right]$

The critical load condition is then distributed on the single part of the repetitive element: the skin contribution is identified for the analysis. This contribution is reported as follows:

$N_{x-SKIN}=\frac{N_{x-cr}p}{\left[E_{p}tp+E_{c}b{s}_1+E_{c}h{s}_2\right]}\frac{E_{p}pt}{p}=\frac{N_{x-cr}}{\left[1+\frac{E_c}{E_p}\frac{b}{p}\frac{s_1}{t}+\frac{E_c}{E_p}\frac{h}{t}\frac{s_2}{p}\right]}$

$\alpha =\left[1+\frac{E_c}{E_p}\frac{b}{p}\frac{s_1}{t}+\frac{E_c}{E_p}\frac{h}{t}\frac{s_2}{p}\right]$

$N_{x-SKIN}=\frac{N_{x-cr}}{\alpha }$

While the other contribution related to the stringer are reported as follows:

$N_{x-C-1}=\frac{N_{x-cr}p}{\left[E_{p}tp+E_{c}b{s}_1+E_{c}h{s}_2\right]}\frac{E_{c}b{s}_1}{p}=\frac{N_{x-cr}}{\left[1+\frac{E_c}{E_p}\frac{b}{p}\frac{s_1}{t}+\frac{E_c}{E_p}\frac{h}{t}\frac{s_2}{p}\right]}\frac{E_c}{E_p}\frac{b}{p}\frac{s_1}{t}=N_{x-SKIN}\frac{E_c}{E_p}\frac{b}{p}\frac{s_1}{t}$

$N_{x-C-2}=\frac{N_{x-cr}p}{\left[E_{p}tp+E_{c}b{s}_1+E_{c}h{s}_2\right]}\frac{E_{c}h{s}_2}{p}=\frac{N_{x-cr}}{\left[1+\frac{E_c}{E_p}\frac{b}{p}\frac{s_1}{t}+\frac{E_c}{E_p}\frac{h}{t}\frac{s_2}{p}\right]}\frac{E_c}{E_p}\frac{b}{p}\frac{s_2}{p}=N_{x-SKIN}\frac{E_c}{E_p}\frac{h}{t}\frac{s_2}{p}$

The second step in the analysis is the determination of the critical load related to the de-bonded plate. Two formulas are considered: the first related to an isotropic plate and the second related to a special orthotropic one.

The critical load related to the isotropic de-bonded plate is according to the well-known formula as in the following:

$N_{x-SKIN-DB}=\frac{{\pi }^2}{{\left(2p\right)}^2}\frac{E_p{t}^3}{12(1-v^2)}{\left(\frac{m}{r}+r\frac{n^2}{m}\right)}^2$

With:

$D_{skin}=\frac{E_p{t}^3}{12(1-v^2)};r=\frac{d}{2p}$

$N_{x-SKIN-DB}=\frac{{\pi }^2}{{\left(2p\right)}^2}{D}_{skin}{\left(\frac{1}{r}+r\right)}^2=\frac{{\pi }^2}{d^2}{D}_{skin}{\left(1+r^2\right)}^2$

The formula is restricted to the m=1 and n=1 according to the common assumption of lower critical load connected to a simply supported plate. The slenderness of the plate is limited to unity due to the fact that higher values are related to substantially constant/bounded critical value. The length of the de-bonded plate is variable in function of the de-bonding dimension “d” as requested by this investigation.

The case of a special orthotropic skin (composite material laminate) coupled with isotropic stringer is analyzed as an example of hybrid structure application. The critical load for the skin in de-bonded area has been calculated using the well-known formula for the simply supported case as in the following:

$N_{x-SKIN-DB}=D_{11}\frac{m^2{\pi }^2}{{\left(d\right)}^2}+2D_0\frac{n^2{\pi }^2}{{\left(2p\right)}^2}+D_{22}\frac{n^4{\pi }^2{d}^2}{m^2{\left(2p\right)}^4}$

The plate stiffness have usual definition as for a composite laminate in special orthotropic lay-up. Assumed values for m=1 and n=1 are considered as in previous derivation to have:

$N_{x-SKIN-DB}=\frac{{\pi }^2}{{\left(2p\right)}^2}\left[D_{11}\frac{{\left(2p\right)}^2}{d^2}+2D_0+D_{22}\frac{d^2}{{\left(2p\right)}^2}\right]$

In this condition the hybrid column Eulerian critical load has been calculated according to the beam-wise approximation for the skin-stinger component. In particular for the specially orthotropic skin, an equivalent elastic modulus is considered as an “Ep” value as follows:

$E_p=\frac{12}{t^3}\left[D_{11}-\frac{D_{12}^2}{D_{22}}\right]$

The final evaluation of the effective de-bonding length for repetitive element requires the definition of a design parameter useful for preliminary design consideration and conclusion. Comparing the two critical load values at the skin side, two observations are possible:

1. If the critical load of the de-bonded skin panel (DB) is lower than the load on the panel in global critical conditions, then local buckling occurs first, so having: $N_{x-SKIN-DB}<N_{x-SKIN}$
2. If the critical load of the de-bonded skin panel (DB) is greater than the load on the panel in global critical conditions, then the global buckling occurs first and the damage is therefore not significant so $N_{x-SKIN-DB}>N_{x-SKIN}$

On this basis a design parameter (PP) that allows to evaluate the damage effectiveness, is defined as follows:

$PP=\frac{N_{x-SKIN}}{N_{x-SKIN-DB}}-1=\frac{{\pi }^2}{l^2}\frac{D_{CC}}{\alpha }\frac{1}{\frac{{\pi }^2}{d^2}{D}_{skin}{\left(1+r^2\right)}^2}-1$

$PP=\frac{N_{x-SKIN}}{N_{x-SKIN-DB}}-1=\left(\frac{d^2}{l^2}\frac{D_{CC}}{D_{skin}}\frac{1}{\alpha {\left(1+\frac{d^2}{l^2}\frac{l^2}{{\left(2p\right)}^2}\right)}^2}\right)-1$

If PP is less than 0, a “Not-significant” damage configuration on the critical load is determined. On the contrary, if there is a local critical condition before the global one (PP higher than 0), therefore the damage remains significant for the global behavior of the repetitive element.

The initial considered configuration is related to isotropic stiffened panel with isotropic repetitive elements. Some initial assumptions are considered: a) the s1 and s2 thickness are considered equal in the stringer due to common manufacturing procedure and due to a similar effect on the critical load for the repetitive element; b) the value of “b” parameter is also considered fixed in order to remain in the T stinger configuration with an effective free portion of the de-bonded panel not influenced greatly by the stringer top-hat dimension; c) a typical “p” dimension of 200mm is assumed representative of the real situations ; d) a reference length of 1000mm is considered as a typical inter-rib distance in the thin-walled wing-box construction. Let's start investigating the “h” effect in a uniform material selection for skin and stringer with a ratio “Ec/Ep” equal to unity. The assumed reference dimensions are as follows: L = 1000mm; p = 200 mm; b = 50 mm; S1=S2 = 3mm; h = variable.

Figure 4 reports the design effectiveness parameter PP for the considered configuration. The slenderness of the de-bonding is limited to 0.4 in order to be realistic in the structural damage effect: a de-bonding dimension higher than 40% of the length is not suitable for the repetitive element as discussed previously. Excessive de-bonding length can induce a failure condition that is different as the considered here. The Ec/Ep parameter is assumed as fixed for each plot starting from 0.5 up to 2.0 while the h values are varied from 5mm to 35mm at constant step.

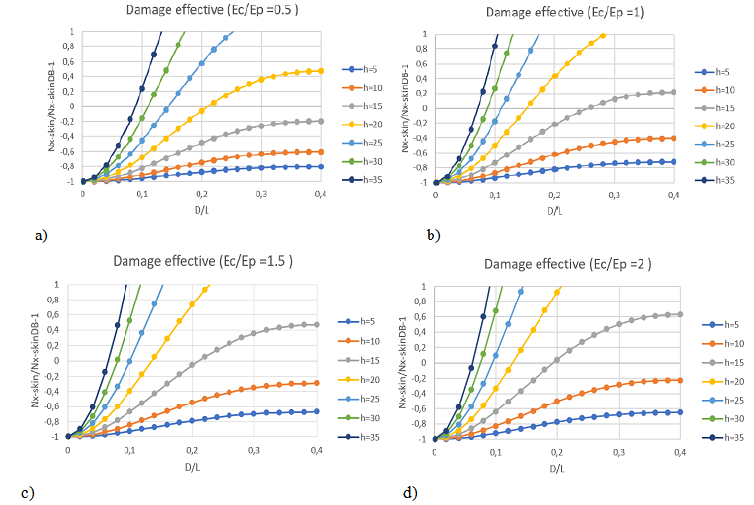
Figure 4 Damage effectiveness (PP) behavior in function of stringer height and material stiffness ratio: a) Ec/Ep=0.5; b) Ec/Ep=1.0; c) Ec/Ep=1.5, d) Ec/Ep=2.0.

A second evaluation is performed considering the h value as fixed as 20mm and varying the Ec/Ep ratio. Two plots are presented in Figure 5, at different skin thickness: t=2mm and t=4mm. The second plot related to t=4mm demonstrate no critical de-bonding length within the considered assumptions.

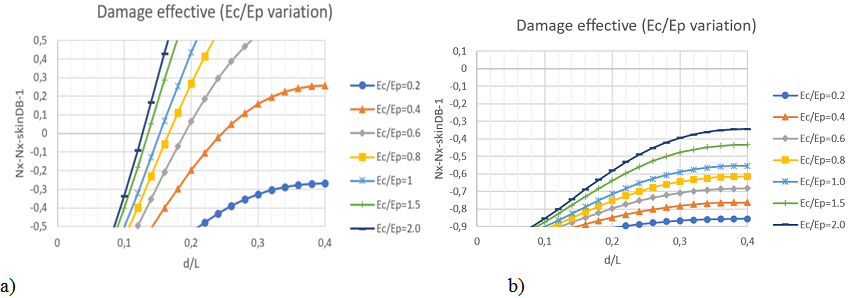
Figure 5 Damage effectiveness parameter (PP) in function of the stiffness ratio for h=20mm, S1=S2=3mm; a) t=2mm; b) t=4mm.

The case of a special orthotropic skin with isotropic stringer is reported in Figure 6 as an example of hybrid structure application. The critical load for the skin in de-bonded area has been calculated using the previous reported formulas. A single value for Ec/Ep ratio is assumed as representative of realistic cases.

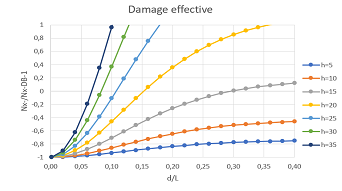
Figure 6 Approximate evaluation of special orthotropic skin case with s1=s2=3mm; t=2mm, Ec/Ep=1.537.

The tendency of producing a short damage length with increasing “h” seems less pronounced with respect to the fully isotropic counterpart at similar Ec/Ep ratio: it can be due to the presence of a critical load higher than its isotropic counterpart in the PP design parameter.

The analysis of the isotropic repetitive element under compressive loads reveals that increasing in “h” dimension a short damage length becomes effective for the global situation. This tendency is in fact related to higher stiff for the stringer with respect to the skin. This is confirmed for each Ec/Ep ratio as reported in Figure 4.

If Ec/Ep ratio is considered as fixed parameter in the repetitive element geometry, a similar behavior is determined if the stringer demonstrates a stiffness higher than the skin. The same tendency is determined for any geometrical parameter influencing the relative stiffness of the stringer.

On the contrary any variation of involved parameters that influences the skin stiffness growth, determines a higher damage length as in the case of Figure 4 b) in which there are not any significant length identified.

In the case of uniform material (Ec/Ep=1), the effective “d /L” parameter remains around 0.145. If the Ec/Ep ratio becomes double that is a double elastic modulus for the stringer with respect to the skin, a significant length ratio equal to 0.12 is found. For a 1000mm long stiffened panel the determined significant de-bonding length is around 120mm. This result, related to the investigated case with 5 stringer p=200mm, gives an interesting general design indication: the significant de-bonding length tends to be within the order of the p – value that is the stringer distance. Lower values are not very significant for the critical load of the panel so it has to be considered not affected by these defect types. Similar results are determined if considering a hybrid configuration with a skin made by special orthotropic laminate. The design parameter PP as in Figure 6 demonstrates similar behavior but mitigated by the considered parameters and ratios.

According to the reported results, it is observed that the defect slenderness depends on the geometric ratios and materials modulus ratio. The obtained results can be viewed as independent of the specific used material. In this way the procedure is assumed as an interesting application from the preliminary design point of view. Equivalent modulus ratio Ec/Ep can be viewed as a main design parameter for the damage effectiveness evaluation. A significant de-bonded length is a function of the skin-to-stringer relative equivalent stiffness at fixed geometrical parameters. Therefore, even using a composite skin and isotropic stringer, the same debonding slenderness would be obtained at a defined equivalent modulus ratio. This feature allows a more general extension of the procedure to preliminary design situations in which there is no data available on the materials, but a reasonable indication of the defect behavior has to be provided.

Such an evaluation remains essential for providing an even approximate indication of the critical defect size related to a specific global property (i.e. the critical load). Structure expected performances are predicted and confirmed with respect to the required structural integrity concepts at a very preliminary design stage. On this basis maintenance procedure and concepts are also identified and adapted to the real situation providing repair/replacement indications. Critical de-bonding size, observed after unexpected loading situation, can be also evaluated by means of the presented procedure in order to assign it to a “significant” or “not-significant” category for the global properties in operative conditions. A maintenance arrangement plan can also be affected by such evaluation.

As reported previously “d/L” greater than 0.4 are impractical in a stiffened panel since they are connected to configurations in which the panel does not contribute to the global critical strength. For such value of d/L, the d/2p ratio exceeds unity and the local critical load of de-bonded skin tends to remain limited or almost constant around the minimum value, oscillating in the range of few percent. This variation can be considered negligible in preliminary design stage so in a first approximation the critical load of de-bonded skin tends to remain constant transferring the applied load to the remaining structure.

Typical skin-to-stringer de-bonding has been analyzed with respect to its effect on the critical load of compressed stiffened flat panels. The damage dimension and size have been evaluated for the definition of a significant value useful in preliminary structural design and dimensioning. The critical local condition of the de-bonded skin has been assumed as detrimental in the global strength of the stiffened plate with critical global load as a reference. A procedure has been defined that compare the local skin load induced by global critical point and the local critical load of the de-bonded skin. The representative proposed design parameter has been reported and investigated as a function of geometrical ratios and modulus ratio of the skin and stringer selected configuration. Fully isotropic and hybrid structural configuration have been analyzed and presented with specific related assumptions consistent to the preliminary design point of view. Significant reference length of de-bonding position has been identified for different structural and geometric configuration in a not-dimensional derivation. The reduction in significant damage size related to high stringer to skin stiffness is presented. Any parameter that influences such a tendency shows similar behavior. In particular, when considering the same elastic modulus ratio for skin/stringer combination, a similar damage size is determined with respect to critical bearing capacity of the whole plate. The dimensionless presented approach is demonstrating very useful and flexible. Potentially extensive applications in the preliminary design stage is also possible for investigating several structural practical cases in similar operating conditions both for dimensioning and for maintenance purposes.

Special thanks to Edoardo for his help in the revision of the language and for iterative activity in clarifying specific presented aspects.

No conflict of interest exists.

1. Romeo G, Frulla G. Postbuckling Behaviour of Graphite/epoxy Stiffened Panels with Initial Imperfections Subjected to Eccentric Biaxial Compression Loading. Int J Non-Linear Mechanics. 1997;32(6):1017‒1033.
2. Yap JWH, Thomson R, Scott ML, et al. Influence of post-buckling behaviour of composite stiffened panels on the damage criticality. Composite Structures. 2004;66:197‒206.
3. Zou D, Bisagni C. Skin-Stiffener Separation in T-Stiffened Composite Specimens in Postbuckling Condition. Journal of Aerospace Engineering. 2018;31(4):04018027.
4. Yaoyao Yea, Weidong Zhua, Junxia Jianga, et al. Computational modelling of postbuckling behavior of composite T-stiffened panels with different bonding methods. Composites Part B: Engineering. 2019;166:247‒256.
5. Frulla G. Structural Behavior of Damaged Anisotropic Stiffened Panels under compressive loads. Proceedings 25th ICAS Congress: Hamburg Germany; 2006.
6. Yap JWH, Scott ML, Thomson R, et al. The analysis of skin-to-stiffener de-bonding in composite aerospace structures. Composite Structures. 2002;57(1-4):425‒435.
7. Abramovich H. Analysis of damage sensitivity and collapse in postbuckling fibrereinforced multi-stiffener panels. Academia;
8. Yetman JE, Sobey AJ, Blake JIR, et al. Investigation into Skin Stiffener Debonding of Top-Hat Stiffened Composite Structures. Composite Structures. 2015;132:1168‒1181.
9. Greenhalgh E, Meeks C, Clarke A, et al. The effect of defects on the performance of post-buckled CFRP stringer-stiffened panels. Composites Part A. 2003;34(7):623‒633.
10. Harley C, Quinn D, Robinson T, et al. The effect of manufacture and assembly joining methods on stiffened panel performance. 32nd International Manufacturing Conference;
11. Frulla G. Buckling and Postbuckling Behavior of Anisotropic rectangular panels under Linearly varying Combined Loads. International Journal of Mechanics and Control. 2005;6(1):13‒20.
12. Frulla G. Experimental behavior of damaged anisotropic rectangular panels under cyclic compressive loads. XVIII AIDAA National Congress;
13. Bisagni C, Giavotto V, Romeo G, et al. Research Activities on Buckling of Composite Structures in Italy. 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference: Palm Springs, California; 2009.
14. Frulla G. Static/Fatigue Structural Behaviour of Damaged Stiffened Composite Plates for UAS Applications. SAE International; 2013.
15. Frulla G, Romeo G. Structural Aerospace Composite/Metallic Samples under Fatigue Loads: Experimental Activity on Three Case Studies. Journal of Mechanics Engineering and Automation. 2014;4(4):318‒326.
16. Bos MJ. Review of aeronautical fatigue and structural integrity investigations in the Netherlands during the period March 2015 - March 2017. NLR-TP-2017-137;
17. Torres M, Franco-Urquiza EA, Hernández-Moreno H, et al. Mechanical Behavior of a Fuselage Stiffened CarbonEpoxy Panel under Debonding Load. J Aerospace Eng. 2018;7:209.
18. Julien Bertolini, Bruno Castanié, Jean-Jacques Barrau, et al. Multi-level experimental and numerical analysis of composite stiffener debonding. Part 1: Non-specific specimen level. Composite Structures. 2009;90(4):381‒391.
19. van Rijn JCFN. Design guidelines for the prevention of skin-stiffener debonding in composite aircraft panels. NLR-TP-2000-355. National Aerospace Laboratory; 2000.
20. Buckling of rectangular specially orthotropic plates. ESDU 80023 Composites Series; 2002.
21. Singer J, Arbocz J, Weller T. Buckling experiments: Experimental methods in buckling of thin-walled structures; shells, built-up structures, composites and additional topics. Volume 2. Wiley; 2002.