Short review of modeling, analysis and prediction of shock structures with multiple reflections of simple waves. Experimental and numerical studies

doi:10.15406/aaoaj.2017.01.00009

eISSN: 2576-4500

Aeronautics and Aerospace Open Access Journal

Mini Review Volume 1 Issue 2

Short review of modeling, analysis and prediction of shock structures with multiple reflections of simple waves. Experimental and numerical studies

OA Azarova

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Department of Mathematical Modeling of Computer Aided Design Systems, Dorodnicyn Computing Centre of the Federal Research Center, Russia

Correspondence: OA Azarova, Leading Scientist, Dorodnicyn Computing Centre of the Federal Research Center, Computer Science and Control of RAS, 119333, Vavilova str. 40, Moscow, Russia, Tel 74991354289

Received: May 12, 2017 | Published: July 28, 2017

Citation: Azarova OA. Short review of modeling, analysis and prediction of shock structures with multiple reflections of simple waves. Experimental and numerical studies. Aeron Aero Open Access J. 2017;1(2):71-74. DOI: 10.15406/aaoaj.2017.01.00009

Download PDF

Abstract

A brief review of experimental and numerical studies of flow structures with multiple reflections of simple waves is presented. Such type of structures arising in quite different experiments and numerical simulations has been specified as a particular aim for the investigations.

Keywords: flow structures, multiple reflection, shear layer, richtmyer-meshkov instability, kelvin-helmholtz instability, miles-ribner instability

Introduction

Theoretical aspects of propagation of waves in the medium containing shear layers have been widely investigated.^1,2 In² steady flow structures with multiple reflection of an acoustic wave have been obtained experimentally on an installation with shallow water. Nevertheless experimental investigations of interaction of waves with shear layers in gases are much less and even less studies containing numerical modeling and analysis of flow structures with multiple reflection (FSMR) arising as a result of the interaction.

Flow structures with multiple reflection of simple waves (compression waves and rarefaction waves) were obtained experimentally and numerically in different cases when a primary wave is dislocated inside the flow area between a flat parallel tangential shock and a hard wall^3,4 or between two contact discontinuities (shear layers).^5,6 Such type of shock structures was discovered in different problems: problems of streamlining a body by a supersonic flow containing an external energy source or in problem of interaction of plane shock wave with the boundary of heated and cold gases or in the situation of Edney IV shock/shock interaction. In some cases of shock wave diffraction these structures haven’t been obtained but prerequisites were created for obtaining these structures.⁷

FSMR obtained in mentioned different problems have mutual features regardless of the type of the condition of their generation. It has been shown that the arising of these structures leads to the space oscillation type of flow parameters: density, pressure and local Mach number which can provide inhomogeneity of the flow up to a turbulence production. Additionally these structures can change aerodynamic characteristics of a body and at some conditions leads to generation of instabilities in the flow. It was shown that the emergence of various types of instabilities may accompany the formation of FSMR: Miles-Ribner instability, Richtmyer-Meshkov instability, Kelvin-Helmholtz instability and others. Thus, the arising of FSMR can be characterized as a dangerous phenomenon especially in aerospace applications because of possibility of the failure of nozzles, changing the mode of combustion of mixtures, changing the characteristics of aerodynamic bodies (which can lead to errors in flight control).

This paper is a short review of the studies in which FSMR were registered, analyzed and could be obtained, experimentally or numerically.

Steady structures with an acoustic wave reflection

Steady flow structures with multiple reflection of an acoustic wave² have been obtained experimentally on an installation with rotating shallow water with a free surface in the fundamental study (see Figure 1a from).² In these experiments an acoustic wave multiple reflects in the cylinder area between the axis of symmetry and a tangential discontinuity. This situation causes generation of the over-reflection instability, or Miles-Ribner instability, where the acoustic wave reflects with an enhancement of its amplitude.

Steady structures with reflection of simple waves

Similar steady structures for simple waves (compression waves and rarefaction waves) in air have been obtained and analyzed numerically for problems of streamlining a plate and a sharpen body by supersonic flow containing an energy source of the shape of a heated rarefied channel (layer)^3,4 (Figures 1, 2, $α_{ρ}$ is the gas rarefaction degree in a heated region). The energy release was suggested to be frozen into the flow and dislocated asymmetrically relatively a body. Mechanism of generation of FSMR in the area between flat tangential shock and hard wall was shown to be connected with the multiple reflections of originally arising and reflecting compression wave. FSMR arising as a result of the asymmetrically located energy deposition are characterized by space oscillation behavior of density, temperature, sound speed and local Mach number .

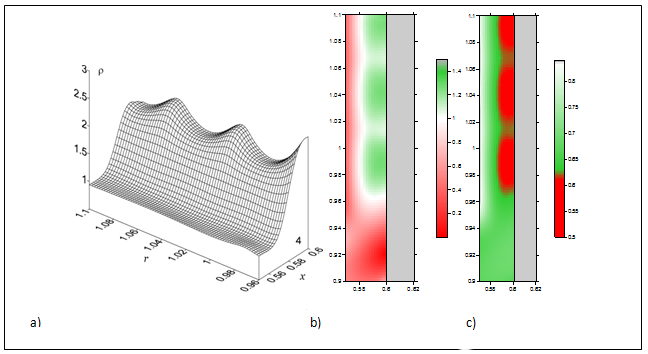
Figure 1 Steady flow structures, supersonic streamlining blunt plate,³ M=1.89, $α_{ρ} = 0. 5$ : a) density, b) local Mach number; c) local sound speed (grey color - body).

Figure 2 Steady FSMR, supersonic streamlining blunt³ and sharpen ⁴ plate. M=1.89, $α_{ρ} = 0. 4$ .

Modeling of unsteady fsmr for edney iv shock/shock interaction

Edney IV interaction type is a short name of the problem of interaction of an impinging shock wave with the bow shock produced by supersonic flow past a sphere, the interaction being supposed to take place in a region where the flow immediately downstream of the bow shock is subsonic. Edney IV shock/shock interaction has been researched in⁵ and the flow details and the body characteristics have been obtained. The scheme of FSMR for Edney IV shock/shock interaction has been described (see Figure 2 from)⁵ and the experimental images of jet bow shock were presented.

Modeling of unsteady fsmr accompanying triple-shock configurations

FSMR have been obtained numerically in problems of interaction of a flat stationary shock wave with a boundary of heated and cold gases for M=7-9⁶ (Figure 3). These structures arise in an area between two contact discontinuities (shear layers) together with triple-shock configurations and accompany a vortex generation. It has been shown that generation of such type of structures in some cases causes the Richtmyer-Meshkov instability together with Kelvin-Helmholtz instability (Figure 4). Effect from additional disturbances on the area of developing the instabilities may lead to the whole flow inhomogeneity resembling turbulence pulsations (Figure 5).

Figure 3 Flow structures with multiple reflections of simple waves.⁶ Density (colors and isochors), left: M=7, $γ = 1.4$ $α_{ρ} = 0. 3$ rarefaction parameter in the energy source αρ; right: M=9, $γ = 1.3$ , $α_{ρ} = 0. 5$ .

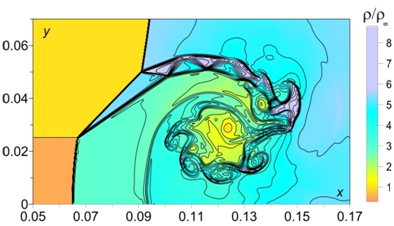
Figure 4 Generation of Richtmyer-Meshkov instability accompanying by Kelvin-Helmholtz instability as the result of FSMR. Density (colors and isochors), M=8, $γ = 1.3$ , $α_{ρ} = 0. 5$ , enlarged.⁶

Figure 5 Inhomogeneous flow region caused by generation of Richtmyer-Meshkov instability accompanying by Kelvin-Helmholtz instability. Density, M=8, $γ = 1.3$ , $α_{ρ} = 0. 5$ .

Conditions leading to prediction of fsmr

In⁷ the process of difraction of plane shock wave on a curved body is researched experimentally. Schematic of the arising flow is presented (see Figure. 11b from)⁷ which is characterised by two shear layers and a lambda-wave which is dislocated inside the area of the shear layers beginning. In can be predicted that the “tail” of the lambda-shock for some Mach number is possible to be a compression wave and its interaction with these shear layers can give rise to the process of multiple reflection of simple waves.

In another case for greater Mach numbers and stronger lambda-wave the conditions of generation of the Richtmyer-Meshkov instability can be possibly fulfiled: interaction of a shock wave dislocated under the angle to the contact discontinuity (shear layer) whith this discontinuity.⁸

Conclusion

Flow structures with multiple reflections (FSMR) of simple waves were obtained in different problems in some cases as additional flow elements which haven’t been the basic research elements. However, in this paper it has been shown that the arising of these structures is of independent interest because it can lead to such phenomena as instabilities, space oscillation type of flow parameters, change of aerodynamic characteristics of an aerodynamic body, turbulent-like fluctuations. Experimental studies specifically of FSMR (for compression and rarefaction waves) have not been conducted. Thus, the study of FSMR for compression and rarefaction waves seems to be extremely important and poorly experimentally and numerically researched yet.