The Network Risk Propagation (NRP) research, combined the theories of Complex Network and the risk propagation, has become one of the main directions in Complex Network study. Is this paper, we introduced the international mainstream research achievements, including the risk propagation threshold-network topology, the NRP-Cascading Failure model, the Immunity from danger in a network-Pinning Control theory. But, about risk source propagation threshold, risk distribution parameter in different networks, early Cascading Failure model and the interaction among different risk systems, are still needed to make forward in order to improve the knowledge about the NRP and reduce its possibility.

Keywords: complex network, risk, propagation, cascading failure, immunity

Through the gradually understanding to the real world, it is beginning to know that the actual structure of many systems expressed in the form of networks. Such as the Internet, the Gene Network, and the Scientists Collaborative Network. However, before the emergence of Complex Network concept, the homogeneous network proposition was more familiar. There are the same characteristics of all units in net with the corresponding significance of all nodes and edges. For a Random Network, because of the equal probability between any two nodes, the degree distribution is a binomial distribution. When the network tends to infinity, the degree distribution of nodes tends to be Poisson distribution. But, after some practical work finished, people gradually found that the majority of real networks degree distributions have power-law characteristics rather than being distributed around an absolute mean value with a certain second-order average. Following with the published paper in Nature, Watts and his mentor Strogatz¹ introduced a small world network model and described the transition from an entirely regular system to a fully Random Network. People realized that the small world network has two features both with the clustering characteristics similar to a regular system and the shorter average path length like Random Network. Later, Barabási & Albert² addressed an article in Science indicated that the degree distribution of many actual Complex Networks obeys the power-law with the scale-free feature. Those systems can be called the Scale-free Network. Since that time, scientists have studied a large number of topological networks, including social networks,^3‒7 information networks,^8‒11 professional networks^12,13 and biological networks,^14,15 and others. The results show that these networks have characteristics such as short feature path, high clustering coefficient, degree correlation and community structures. These discoveries have significantly contributed to the study of Complex Networks. The Complex Network and other related network research methods had become one of the main tools for the study of complex systems. Lots of Complex Network models have emerged and caused people’s attention.^16‒19 Due to the in-depth understanding of the network structure, there are a variety of dynamic processes in the system and the cross-integration with other disciplines in recent years. Researchers studied the single or group dynamics behavior and processes on the network by considering the Complex Network as a dynamical system or quoting moving units into the network, including Communication, Chaos, Robustness, Fractal, Cascading Failures, and Synchronization. Explored the structural characteristics of the whole system and forecasted the links through the analysis about the critical nodes and paths. Designed new algorithms to optimize the network structure and improved the performance, especially regarding stability, synchronization, and data.

Risk usually refers to the probability of uncertainty between the purpose and the expected return. It emphasizes the possibility of the loss and income. Therefore, we can divide the risk into two categories: the Narrow and the Generalized. The Narrow Sense of Risk mainly refers to the uncertainty of the loss. The Generalized covers the uncertain attributes both of loss and benefit. In this paper, the network risk with the spreading capability, which we talked about, belongs to the narrow scope. The main content is the risk propagation process in the system and the realization of its "Immunity." Here, the "Immunity" of the NRP refers to the loss of the local network unit in the process of specifying the NRP is less or no impact and continue to maintain the initial state.

Traditional international researchers focused their views on the risk assessment, which means providing data that can be easily relied upon and understood to decision makers for risk judgments. Now, researchers tend to combine the network theory with the risk assessment demands. The way is mainly because the carriers of risk propagation are often associated with each other to form a network. They also can overcome the limitations of computing conditions and make an exceptional uncertainty event analysis results. They have a wider applicability,²⁰ making the cause and effect of risk become visualized to facilitate the identification of high-weighting or critical components of events.²¹ Among them, "Bow," Causal Map, Bayesian Network (directed non-circular network) and Fault Tree are the typical combination methods of the network theory and risk assessment.²²

Network propagation components include Risk Sources, Propagation Node, Propagation Media (or Propagation Adaptation Conditions), and Risk Recipients. If the propagation conditions of risk are not sufficient, then its ability will be declined. When the risk has a spread attribute, combined with a specific network, with the propagation conditions, it will form a particular Risk Propagation Network (RPN). In Figure 1, it introduces an NRP process based on a risk propagation environment. The First Layer of Risk Propagation Network (RPNL1) that is the unit in the network has a substantial risk of breeding performance, or first risk-affected and produced greater damage effectiveness. In the absence of other external forces, the risk spreading power and the devastating effects of the second layer (RPNL2) is weaker than the first.

Figure 1 The NRP process of exogenous risk based on the risk propagation environment. We assume the constituent nodes of the risk distribution network are equipped with a risk-transmitting ability and have an influence on each other. Plus, we presumed that the NRP thresholds are independent of each other. When a risk erupts, the risk which can break through the threshold, with the propagation ability, will be first transmitted to a network carrier. When the second level of risk dispersion limit broke, the risk began to spread to the second layer of a network, and gradually formed a Two-layer Risk Propagation Network, then, continued the process. As the risk distribution evolves, the potential for breeding is attenuated until it will not be disseminated. (This figure only indicates the risk allocation process which based on the network nodes, without the edges process.)
The risk may originate from various uncertainties factors within or outside the system so that it includes into Endogenous (ENR) and Exogenous Risks (EXR). The ENR is mostly due to the link break between the internal network subject, such as financial risks, information systems errors, and human errors. The EXR derived from environmental changes outside the system, such as natural disasters, war, epidemic outbreaks, etc. The main characteristic of EXR is that the network does not control them. But the system subject can reduce the loss or the risk propagation probability under certain conditions, and even achieve the goal of “Immunity." Because EXR often needs to break through the "first-level risk distribution threshold," so it is more common. It is essential can be controlled by the central network subject.

The risk may originate from various uncertainties factors within or outside the system so that it includes into Endogenous (ENR) and Exogenous Risks (EXR). The ENR is mostly due to the link break between the internal network subject, such as financial risks, information systems errors, and human errors. The EXR derived from environmental changes outside the system, such as natural disasters, war, epidemic outbreaks, etc. The main characteristic of EXR is that the network does not control them. But the system subject can reduce the loss or the risk propagation probability under certain conditions, and even achieve the goal of “Immunity." Because EXR often needs to break through the "first-level risk distribution threshold," so it is more common. It is essential can be controlled by the central network subject.

In different systems, there are various risks. In the field of Complex Networks, the analysis of the spread of exogenous risks, such as about the epidemic diseases¹ and information²,^23‒26 are dominated by diffusion studies of interpersonal networks.^27‒29 Those works are focused because the propagation of epidemic or information is closely related to network, and similar to the spread of computer viruses in some extent, so the researchers have given more attention to this issue. Among them, Pastor Satorras and others did a lot of work in this area. They start from the simplest form of SI (Susceptible-infected) model, then applied the relevant models to network research, including SIR (susceptible-infected-recovered) model, SIS (Susceptible-infected-susceptible model, SIRS (Susceptible-Infected-Removed- Susceptible) model and SEIR (the SIR model including the effects of exposed individuals) model.^30‒33 Now, network risk research has gradually extended to other areas.^34‒38 However, for specific systems, researchers tend to choose the analysis of endogenous risks, such as a financial risk in an economic system³⁹ and flight delays in air transport networks(ATN) (Figure 2).^40‒42

Figure 2 Diagrammatic representation of different epidemic models regarding reaction-diffusion processes. Boxes stand for different compartments, while the arrows represent transitions between compartments, happening stochastically according to their respective rates.³³

¹Most of the literatures cited in this paper use the virus as the main research object of network risk propagation.

²The application of information also has the uncertainty of income and loss, which belongs to the generalized risk scope. But in this article, the cited mainly carry out the research in the narrow category of risk. 

The threshold of an NRP-the Network Topology

The risk propagation in the network is closely related to the network's topology. Researchers^43‒46 have found that because of the risk distribution thresholds in conventional systems and Random Networks, the risk can only be propagated in the network when it exceeds the threshold. This dispersion limit usually represents the infection level of the network node. However, in the Scale-free Network, it cannot find a clear propagation threshold, or can be considered there is a lower distribution limit, so the network risk is more likely to spread in the Scale-free Network, or even long-term exists. In a small world network, the proliferation of network risk is easier than in the regular system with higher speed. The root of the difference in the NRP is the difference of network topology. There are some studies^47‒49 about the relationship between the NRP and the topological network structure as well as the problem of network adaptive cooperative evolution. The results show that the interaction which between network topology and node dynamics produces richer dynamical behavior. The risk propagation process of systems is more complicated with self-organizing feature and adaptive cooperative behavior.^50‒52 In the adaptive system, the behavior of the individual to avoid the infection will make an appropriate adjustment of the network structure, which can inhibit the spread of the risk; the propagation process will appear bistable and oscillation domain which does not exist in the static network. Also, another typical feature-community structure also has an impact on the spread of network risk. Zhonghua Liu⁵³ outcropped that the community structure in a network has a great impact on the risk dissemination. The presence of the web community will reduce the propagation threshold, as well as the final size of infection. Salathé⁵⁴ found that in the community structure system, the infection density has stabilized at a fixed equilibrium point or exhibits periodic oscillation, unstable oscillation due to the decrease of propagation threshold and the increase of the NRP rate. Rocha⁵⁵ discovered that the spread of network risk infection has a relationship with the size of the network community. The most widely used theoretical approaches include the mean-field, the heterogeneous mean-field, the quench mean-field, dynamical message-passing, link percolation, and pair wise approximation. The cross-integration of the method itself has also become a concern for scholars now (Figure 3).⁵⁶

At the same time, researchers also studied the close relationship between the Robustness or Survivability of the network with the spread of network risk. The study began with the work of Albert et al.⁵⁷

They modeled ER and BA Networks under two types of attack strategies. One is random failure policy that is an entirely accidental removal of part of the network nodes, which corresponds to the network nodes random failure. The other is deliberate attack strategy, which means we will remove the node with the degree value in descending order. They measure the Robustness or Survivability of network by the average path length change, the ratio of the size of the maximum connected subgraph and the system, and the percentage of the removal nodes to the total number in the original network. In the case of random failure, the Scale-free Network is more robust than the Stochastic Network. It is because of the extreme non-uniformity of the degree distribution in the Scale-free Network. The vast majority of nodes have minimal degree values, and only a few nodes have big ones. In deliberate attack way, the Scale-free Network crash faster than the Random. As long as some parts of nodes removed with high values, the entire network will be paralyzed for its significant impact on the connectivity. This higher vulnerability is also due to the extreme non-uniformity of the degree distribution. Therefore, the severe non-uniformity of the node degree of the Scale-free Network creates the Robustness in not only the random failure but also a high level of vulnerability in deliberate attacks. Many scholars have concerned Albert's research. Gradually, there are some researchers use this method to carry out the work on specific issues.^58‒61 But about the node removal criteria, it was replaced by other ways. It is because the node degree is no longer the only method to measure its importance in the whole network. The critical nodes in many real networks are not with greater intensity values.^59,60 At the same time, there are scholars promoted research on the attack strategy itself to get a more general form. By defining a node probability distribution function, the analytical and simulation methods are used to analyze the network collapse threshold under different network risks.⁶² Some scholars have investigated the relationship between Complex Network topology, and its Robustness from system spectral measure and proposed a Robustness optimization method based on Taboo Search (Figure 4).⁶³

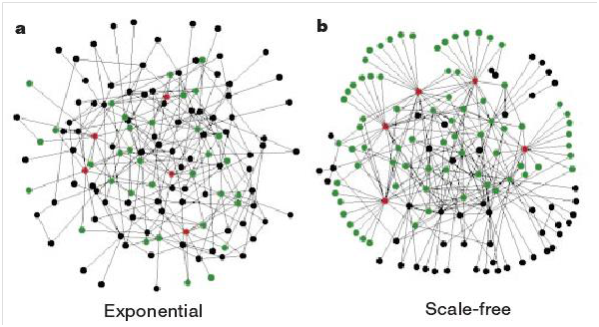
Figure 3 Visual illustrates the difference between an exponential and a scale-free. A. The Exponential Network is homogeneous: most nodes have approximately the same number of links. B, the Scale-free Network is inhomogeneous: the majority of the nodes have one or two links, but a few nodes have a large number of links, guaranteeing that the system is fully connected. Red, the five nodes with the highest number of links; Green, their first neighbors. Although in the Exponential Network only 27% of the nodes are reached by the five most connected nodes, in the Scale-free Network more than 60% is achieved, demonstrating the importance of the connected nodes in the Scale-free Network.⁵⁷ At the same time, researchers also studied the close relationship between the Robustness or Survivability of the network with the spread of network risk. The study began with the work of Albert et al.⁵⁷ 

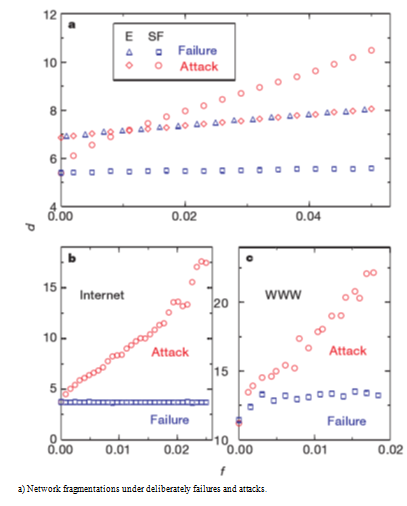
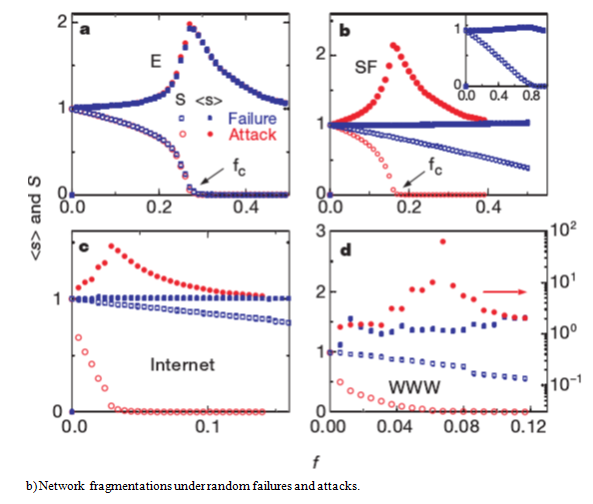
Figure 4 The diameter changes and network debris in Albert experiments based on different attacks on the system.⁵⁷

The process of the NRP-cascading failure models

Many scholars have paid attention to Cascading Failure phenomenon in the course of the NRP. One of the main concerns is the reproductions by Cascading Failure models which connected with different causes. Scholars analyze these problems from the node or edge overload. Moreno⁶⁴ proposed a Cascading Failure model for a BA Scale-free Network. This model is a dynamic model of load-capacity nodes, which gives a security threshold for each node satisfying the Weber distribution. The load is the ratio of the external action of the total number of nodes in the network. If the node load is greater than the security threshold, it indicates that the node has failed. When the node fails, it will be removed from the network's maximum connected subgraph with the load passing to the neighbors. The redistribution of node weight may cause failures of non-faulty nodes, resulting in Cascading Failures. When the load of all unreserved nodes in the network is less than the security threshold, the Cascading Failure disappears, and the system reaches the equilibrium state. Many scholars improved the average redistribution of node loads in this model. Motter⁶⁵ assumes that the information or energy exchanged between the nodes along the geodesic (short-range). The weight of the node is the number of nodes, and the capacity of the node is the maximum load that the node can carry, which is proportional to its original amount. Usually, the network will run in its flow state. When a node fails, it will lead to the shortest path of the network distribution changes; the network fault-free node load may also change. Likewise, when the node load exceeds its capacity, the node will fail, causing a new redistribution of the node weight. If the network node weight distribution is and the burden of the removal node is high, it will lead to Cascading Failure.

Later, Moreno⁶⁶ studied the Cascading Failure of the BA Scale-free Network due to the congestion of the edges. Instead of giving a load to nodes but the side, the capacity is subject to a statistical distribution. Define the ability of each side is 1. If the side of the load exceeds the capacity, it indicates congestion, so you need to follow certain dynamic rules to re-distribution of the burden. If all adjacent edges are congested, you have to discard them or make the amount globally allocated to the other edges without any congestion. The redistribution of the load may cause other edges congestion, resulting in Cascading Failures. If more congestion occurs, the network will not have a widely connected subgraph. Crucitti⁶⁷ proposed a dynamic Cascading Failure model considering both the node and the edge. The model uses the undirected weight graph to represent the general propagation network. The larger the edge weight, the higher the efficiency of the information distribution. He defined the number of the optimal path of the node load for a particular time and the evolution formula of the edge weight. When a node in the network fails, the optimal path between the nodes in the network will change, resulting in a redistribution of the load, which may lead to pressure overloading of other regular nodes and then cause new charge redistribution, resulting in Cascading Failure. After the Cascading Failure, the average efficiency of the network is measured to estimate the degree of interdependent system damage. Scala⁶⁸ extends the model of the Cascading Failure behavior due to overload to the secondary system. Tang⁶⁹ designed the load propagation of the failed node through the interdependent network and developed the priority redistribution strategy. In the network layer and the physical layer network, using a pair of directional dependencies between the giant functional components and the nodes to quantify the risk propagation process in the secondary system to construct the time-varying polynomial equation. Scala⁶⁸ considered load distribution via connectivity links as node failure spreads through an interdependent system, and developed a priority redistribution strategy for failed charges subject to flow constraint. Using a giant component function and a one-to-one directed interdependence relation between nodes in a cyber-layer network and physical-layer network, they constructed time-varied functional equations to quantify the dynamic process of failed loads propagation in an interdependent system.

The avoidance of the NRP–the “Immunity”

The early work on the "Immunity" research on the NRP stems from the study of Robustness and Survivability of the network. In addition to the preceding, the analysis of the differences in the characteristics of network nodes in risk propagation has become one of the hot spots in the research of "Immunity." Salathé⁷⁰ find that community structure has a significant impact on risk dynamics. And in networks with strong community structure, immunization interventions targeted at individuals bridging communities are more effective than those simply targeting highly connected people. Kitsak⁷¹ studied the influence level of nodes on the risk propagation of the network. It points out that in the case of one breeding source in a network, the influential nodes often determined by the K-shell decomposition, not by higher values of betweenness or degree. Gradually, the identifications of critical nodes⁷² and paths⁷³ have attracted attention. The specific algorithms designed by the researchers ranging from only counting the nearest neighbors to complicated machine learning and message passing approaches,⁷⁴ which further advances the study of network Pinning Control. Pinning Control in the system is a concept to control some of the primary nodes to achieve the domination of the whole network dynamics.⁷⁵

Wang⁷⁶ and Li⁷⁷ have studied the feasibility and effectiveness of the network Pinning Control. The research shows that some nodes linear feedbacks can stabilize the whole system in the synchronous state. As long as the coupling strength and feedback control gain of the scheme is suitable, it is possible to achieve control objectives only by some nodes. Parekh & Sinha⁷⁸ expand the anti-control of the spatiotemporal chaos control of the coupled image lattice, that is, the coupled model lattice becomes a chaotic state or further enhances its chaos by Pinning Control. Chen⁷⁹ and Zhan⁸⁰ point out that only one node of the network can be controlled to bring the system to a synchronized state. Zhan⁸⁰ also examines the parameters required for the system to reach the synchronization state if the internal coupling function is different. Liu⁸¹ and Xiang⁸² generalize the Pinning Control idea to the coupled matrix of the weighted network with time delay and the network that cannot be diagonalized. Lu⁸³ applies the Pinning Control to the dynamic adaptive system. In addition to adding a control to a small number of nodes, the state update of each node in the network only depends on the situation of the neighbor. Yuan⁸⁴ studied the feasibility of Pinning Control in the interdependent network that only needs to strengthen a small part of the node; it can prevent the sudden catastrophic collapse of the system.

Some scholars have also focused on other cyber dynamics based on Pinning Control theory. Xuan⁸⁵ puts forward the concept of reaction infiltrated network structure control and affects the dynamic behavior by controlling the network structure. Xi Yugeng⁸⁶ explores the problem of structural decomposition, Complex Network structure monitoring, and containment control by using big system control theory, and has improved the algorithm of redundant control column by using standard mark method to a high system control theory. He tried to use the improved target method to solve the problem of controllability of Complex Networks and analyze the problems and difficulties in using this approach to solve the Controllability of Complex Networks. Chen⁸⁷ explain the new challenges encountered in the research and control of hyper-network systems composed of controllability, containment monitoring and network coupling of several different properties or different scales. Giulia⁸⁸ mapped the problem and constructed the theoretical framework of the linear controllability in a multilayer network.

In this review, we have extensively discussed the state-of-the-art progress in risk propagation in networks, emphasizing on three related scopes in this area. In this section, we show some critical challenges for future studies.

Firstly, we need to define the propagation threshold of the risk source. The spread of network risk requires a source of risk and distribution media. Usually, the scholars are more concerned about the network carrier, instead of the risk self. The same risk source-virus is the basis of many of results mentioned before. However, there are still have some specific system risks are distinguished from the virus. Different systems are facing attacks from various hazards. For a reason, that study of the risk source needs to be strengthened in future to make a better explanation. What characteristics and propagation effects of risks will have an impact on specific networks to form a typical RPN? It relates to the defining the distribution threshold of the risk source. To some extent, this problem can be equivalent to the network's Survivability assessment. But for specific systems, it needs to develop in-depth. If we can predict the anti-destructive ability indicators of a particular system and the damaging effect of a specific risk, give an identified prevention methods with data, it will greatly help to reduce the probability of risk propagation and the loss.

Secondly, it needs to pay more attention to the risk distribution adaptation conditions in the network. It is an unavoidable problem to analyze when we are trying to define the definition of the NRP threshold. The risk with the same spread power will have different effects in different network carriers. At the same time, the impact of various propagation conditions on risk distribution is inevitable. However, there are few studies about it. Researchers can explore the key factors, and the concrete means to reduce the probability of the NRP by analyzing its adaptability.

Thirdly, the new gradual process research of the NRP needs further development. The impact of the NRP reflects in the node or edge. Many scholars often take the method by remove nodes or edges to simulate the risk propagation process^89,90 and then analyze the changes of the network. Notwithstanding, the risk performance is a gradual process essentially. It requires both a measure of the risk propagation threshold and an analysis of the survivable effort of nodes or edges based on the specific adaptation conditions. Only the risk spreads power can break through the NRP threshold, the nodes or edges will be affected. Although the real process of the NRP is often extremely rapid, it is still gradually in fact. For example, in an ATN, the congestion is often causing its operational efficiency declining rather than paralyzed directly. And therefore, it is of course not equivalent to the nodes or edge failures by an acute attack or other causes. It can be defined as an Early Cascading Failure Process and still lacked the research in detail. At the same time, the Cascading Failure process of the NRP also needs to do further exploration.

Lastly, we are longing for some real large-scale applications of the mentioned studies in the real world. Although we talked, many studies are used to solve some other problems, most of which are far from practical applications. What we mean real applications here is that the obvious risk propagates in an exclusive network or it’s intersect spread in different networks, such as the risk of volcanic eruptions on ATN, and its spread from ATN to other transport systems. In the final analysis, successful applications will primarily encourage related studies.

This work is funded by the Philosophy and Social Science Fund for Universities in Jiangsu Province, China (Grant No. 2016SJD790002), China Postdoctoral Science Foundation (Grant No. 2016M591844), Jiangsu Natural Science Foundation (Grant No.BK20151479) and the Fundamental Research Funds of Central Universities in China (Grant No.NZ2016109, NJ20160085 and NS2017074). Also, we thank for the support of the Fourteenth Batch of the High-level Talent Fund in the Six Talent Peaks Project (Grant No. SZCY-005) and the Sponsorship of Overseas Research & Training Programme for University Prominent Young & Middle-aged Teachers and Presidents in Jiangsu, China.

Author declares that there is no conflict of interest.

1. Watts DJ, Steven HS. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–442.
2. Barabási AL, Réka A. Emergence of scaling in Random Networks. Science. 1999;286(5439):509–512.
3. Newman MEJ, Strogatz SH, Watts DJ. Random graphs with arbitrary degree distributions and their applications. Physical review E. 2001;64(2):026118.
4. Barabâsi AL, Jeong H, Neda Z, et al. Evolution of the social network of scientific collaborations. Physica A: Statistical Mechanics and its Applications. 2002;311(3):590–614.
5. Girvan M, Mark EJ Newman. Community structure in social and biological networks. Proceedings of the national academy of sciences. 2002;99(12):7821–7826.
6. Gerald DF, Yoo M, Wayne E Baker. The small world of the American corporate elite, 1982-2001. Strategic Organization. 2003;1(3):301–326.
7. Ohtsuki H, Hauret C, Lieberman E, et al. A simple rule for the evolution of cooperation on graphs and social networks. Nature. 2006;441(7092):502–505.
8. Albert R, Hawoong J, Barabási AL. Diameter of the world-wide web. Nature. 1999;401(6749):130–131.
9. Barabási, AL, Albert R, Hawoong Jeong. Scale-free characteristics of Random Networks: the topology of the world-wide web. Physica A: statistical mechanics and its applications. 2000;281(1-4):69–77.
10. Adamic LA, Bernardo AH, Barabási AL. Power-law distribution of the world wide web. Science. 2000;287(5461):2115–2115.
11. Jaffe Adam B, Manuel T. Patents, citations, and innovations: A window on the knowledge economy. MIT press; 2002.
12. Latora V, Massimo Marchiori. Is the Boston subway a small-world network?. Physica A: Statistical Mechanics and its Applications. 2002;314(1):109–113.
13. Guimerà R, Mossa S, Turtschi A, et al. The worldwide air transportation network: Anomalous centrality, community structure, and cities' global roles. Proceedings of the National Academy of Sciences. 2005;102(22):7794–7799.
14. Jeong H, Tombar B, Albert R, et al. The large-scale organization of metabolic networks. Nature. 2000;407(6804):651–654.
15. Jeong H, Mason SP, Barabási AL, et al. Lethality and centrality in protein networks. Nature. 2001;411(6833):41–42.
16. Newman MEJ. The structure and function of Complex Networks. SIAM Review. 2003;45(2):167–256.
17. Ravasz E, Barabási AL. Hierarchical organization in Complex Networks. Physical Review E. 2003;67(2):026112.
18. Boccaletti S, Latora V, Moreno Y, et al. Complex Networks: Structure and dynamics. Physics reports. 2006;424(4):175–308.
19. Barabási AL. Scale-free Networks: a decade and beyond. Science. 2009;325(5939):412–413.
20. Meyers LA, Newman MEJ, Stephanie S. Applying Network Theory to Epidemics: Control Measures for Mycoplasma Pneumoniae Outbreaks. Emerging Infectious Diseases. 2003;9(2):204–210.
21. Human Factor Issues, NATO Advanced Science Institutes, Series F: Computer and System Sciences, Vol. 110. New York: Springer Verlag; 2005. 35–60 p.
22. Newman MEJ. Networks: an Introduction. Oxford: Oxford UP; 2010.
23. Moreno Y, Nekovee M, Pacheco AF. Dynamics of rumor spreading in Complex Networks. Physical Review E. 2004;69(6):066130.
24. Sudbury A. The proportion of the population never hearing a rumour. Journal of applied probability. 1985;22(2):443–446.
25. Zanette DH. Critical behavior of propagation on small-world networks. Physical Review E. 2001;64(5):050901.
26. Liu Z, Lai YC, Ye N. Propagation and immunization of infection on general networks with both homogeneous and heterogeneous components. Physical Review E. 2003;67(3):031911.
27. Dewri R, Nayot P, Ray I, et al. Optimal security hardening using multi-objective optimization on attack tree models or networks. In: Proceedings of the 14th ACM Conference on Computer and Propagations Security; 2007. 204–213 p.
28. Nayot P, Rinku D, Indrajit R. Dynamic security risk management using bayesian attack graphs. IEEE Transactions on Dependable and Secure Computing. 2012; 9(1):61–74.
29. Raymond C, Guofu Z. Modeling of non-normality using multivariate t: Implications for asset pricing. China International Finance Review. 2017;7(1).
30. Pastor-Satorras R, Alexei V, Alessandro V. Dynamical and correlation properties of the Internet. Physical review letters. 2001;87(25):258701.
31. Pastor-Satorras R, Alessandro V. Immunization of Complex Networks. Physical Review E. 2002;65(3):036104.
32. Brooks BR, Brooks CL, Mackerell AD, et al. CHARMM: the biomolecular simulation program. Journal of computational chemistry. 2009;30(10):1545–1614.
33. Pastor-Satorras R, Claudia C, Piet Van M, et al. Epidemic processes in Complex Networks. Reviews of Modern Physics. 2015;87(3):925.
34. Christakis NA, James HF. The spread of obesity in a large social network over 32 years. New England journal of medicine. 2007;357(4):370–379.
35. Claudia C, Fernanda S. Supply chain risk management: a new methodology for a systematic literature review. Supply Chain Management: An International Journal. 2012;17(4):403–418.
36. O'Dea R, Crofts JJ, Kaiser M. Spreading dynamics on spatially constrained complex brain networks. Journal of the Royal Society Interface.2013;10(81):20130016.
37. Lei Kai, Zhu Xiaoning, Hou Jianfei. Modeling and Simulation of Risk Propagation in Multimodal Transportation Networks. Journal of Transportation Systems Engineering and Information Technology. 2016;10(3).
38. Meier J, Zhou X, Hillebrand A, et al. The Epidemic Spreading Model and the Direction of Information Flow in Brain Networks. Neuroimage. 2017;152:639–646.
39. Cambini C, Yanyan Jiang. Broadband investment and regulation: A literature review. Telecommunications Policy. 2009;33(10):559–574.
40. Ahmad Beygi S, Cohn A, Guan Y, et al. Analysis of the potential for delay propagation in passenger airline networks. Journal of air transport management. 2008;14(5):221–236.
41. Pyrgiotis N, Kerry MM, Amedeo O. Modelling delay propagation within an airport network. Transportation Research Part C: Emerging Technologies. 2013;27:60–75.
42. Bongiorno C, Gurtner G, Lillo F, et al. Statistical characterization of deviations from planned flight trajectories in air traffic management. Journal of Air Transport Management. 2017;58:152–163.
43. Pastor-Satorras R, Vespignani A. Epidemic dynamics and endemic states in Complex Networks. Physical review E. 2001;63:066117.
44. Boguá M, Pastor-Satorras R. Epidemic spreading in correlated Complex Networks. Physical review E. 2002;66:047104.
45. Newman MEJ. Spread of epidemic disease on networks. Physical Review E; 2002. 12 p.
46. Zhao Gang. Research on Dynamic Behavior of Complex Supply Chain Network and Its Controllability. China: Nanjing University of Aeronautics and Astronautics; 2015
47. Shaw Leah B, Schwartz Ira B. Fluctuating epidemics on adaptive networks. Physical review E. 2008;77:066101.
48. Shaw Leah B, Schwartz Ira B. Enhanced vaccine control of epidemics in adaptive networks. Physical review E. 2010;81(4):046120.
49. Jolad S, Liu W, Schmittmann B, et al. Epidemic spreading on preferred degree adaptive networks. PLoS One. 2012;7(11):e48686.
50. Zhong-Hua L, Bambi HU. Epidemic Spreading in Community Networks. Europhysics Letters. 2005;72(2):315.
51. Zhou Yin-Zuo, Zong-Hua L, Zhou Jie. Periodic Wave of Epidemic Spreading in Community Networks. Chinese Physics. 2007;24(2):581.
52. Salathé Marcel, Jones James H. Dynamics and control of diseases in networks with community structure. PLoS computational biology. 2010;6(4):e1000736.
53. Zhong-Hua L, Bambi HU. Epidemic Spreading in Community Networks. Europhysics Letters. 2005;72(2):315.
54. Salathé Marcel, Jones James H. Dynamics and control of diseases in networks with community structure. PLoS computational Biology. 2010;6(4):e1000736.
55. Rocha Luis EC, Anna ET, Renaud L, et al. Respondent‐driven sampling bias induced by community structure and response rates in social networks. Journal of the Royal Statistical Society: Series A (Statistics in Society). 2017;180(1):99–118.
56. Wang W, Tang M, Stanley HE, et al. Unification of theoretical approaches for epidemic spreading on Complex Networks. Reports on Progress in Physics. 2017;80(3):036603.
57. Albert R, Hawoong J, Barabási AL. Error and attack tolerance of Complex Networks. Nature. 2000;406(6794):378–382.
58. Schneider CM, Andre AM, Jose SA, et al. Mitigation of malicious attacks on networks. Proceedings of the National Academy of Sciences. 2011;108(10):3838–3841.
59. Wilkinson SM, Sarah D, Shu Ma. The vulnerability of the European air traffic network to spatial hazards. Natural Hazards. 2012;60(3):1027–1036.
60. Lordan O, Jose MS, Simo P, et al. Robustness of the air transport network. Transportation Research Part E: Logistics and Transportation Review. 2014;68:155–163.
61. Yuan X, Yang D, Stanley E, et al. k-core percolation on Complex Networks: Comparing random, localized, and targeted attacks. Physical Review E. 2016;93(6):062302.
62. Gallos LK, Cohen R, Panos A, et al. Stability and topology of Scale-free Networks under attack and defense strategies. Physical Review Letters. 2005;94(18):188701.
63. Jun W, Yuejin T. Study on measure of Complex Network invulnerability. China: National University of Defense Technology; 2005.
64. Yuejin T, Wu J, Deng H. Progress in invulnerability of Complex Networks. Journal of Shanghai University for science and Technology. 2011;33(6):653–668.
65. Moreno Y, Gómez JB, Pacheco AF. Instability of Scale-free Networks under node-breaking avalanches. Europhysics Letters. 2002;58(4):630.
66. Motter AE, Lai YC. Cascade-based attacks on Complex Networks. Physical Review E. 2002;66(6):065102.
67. Moreno Y, Pastor-Satorras R, Vázquez A, et al. Critical load and congestion instabilities in Scale-free Networks. Europhysics Letters. 2003;62(2):292.
68. Crucitti P, Latora V, Marchiori M. Model for Cascading Failures in Complex Networks. Physical Review E. 2004;69(4):045104.
69. Scala A, et al. Cascades in interdependent flow networks. Physica D: Nonlinear Phenomena. 2016;323:35–39.
70. Tang L, Jing K, Jie H, et al. Complex interdependent supply chain networks: Cascading Failure and Robustness. Physica A: Statistical Mechanics and its Applications. 2016;443:58–69.
71. Salathé M, Jones JH. Dynamics and control of diseases in networks with community structure. PLoS Comput Biol. 2010; 6(4):e1000736.
72. Kitsak M, Gallos LK, Havlin S, et al. Identification of influential spreaders in Complex Networks. Nature physics. 2010;6(11):888–893.
73. Linyuan L, Zhou T, Qian-Ming Z, et al. The H-index of a network node and its relation to degree and coreness. Nature propagations. 2016;7.
74. Witthaut Dirk. Critical links and nonlocal rerouting in complex supply networks. Physical review letters. 2016;116(13):138701.
75. Lü Linyuan, Duanbing Chen, Xiao-Long Ren, et al. Vital nodes identification in Complex Networks. Physics Reports. 2016;650(13):1–63.
76. Wang XF, Chen G. Pinning Control of scale-free dynamical networks. Physica A: Statistical Mechanics and its Applications. 2002; 310(3):521–531.
77. Li X, Wang X, Chen G. Pinning a complex dynamical network to its equilibrium. IEEE Transactions on Circuits and Systems I: Regular Papers. 2004;51(10):2074–2087.
78. Parekh N, Sinha S. Controlling spatiotemporal dynamics in excitable systems. Phys Rev E. 2002;65:036227.
79. Chen T, Liu X, Lu W. Pinning Complex Networks by a single controller. IEEE Transactions on Circuits and Systems I: Regular Papers. 2007;54(6):1317–1326.
80. Zhan M, Gao J, Wu Y, et al. Chaos synchronization in coupled systems by applying Pinning Control. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76(3):036203.
81. Liu ZX, Chen ZQ, Yuan ZZ. Pinning Control of weighted general complex dynamical networks with time delay. Physica A: Statistical Mechanics and its Applications. 2007;375(1):345–354.
82. Xiang LY, Liu ZX, Chen ZQ, et al. Pinning Control of complex dynamical networks with general topology. Physica A: Statistical Mechanics and its Applications. 2007;379(1):298–306.
83. Lu W. Adaptive dynamical networks via neighborhood information: Synchronization and Pinning Control. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2007;17(2):023122.
84. Xin Yuan, Yanqing Hu, H Eugene Stanley, et al. Eradicating catastrophic collapse in interdependent networks via reinforced nodes. Proceedings of the National Academy of Sciences. 2017;114(13):3311–3315.
85. Xuan Q, Du F, Dong H, et al. Structural control of reaction-diffusion networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2011;84(2-3):036101.
86. Xi Yugeng, Large-scale Systems Control and Complex Networks-Exploration and Thinking. Acta Automatic Sinica. 2013;39(11):1758–1768.
87. Chen Guanrong. Problems and Challenges in Control Theory under Complex Dynamical Network Environments. Acta Automatic Sinica. 2013;39(4):312–321.
88. Menichetti Giulia, Luca Dall Asta, Ginestra Bianconi. Control of multilayer networks. Scientific reports. 2016;6.
89. Bo Cui. Centrality of China aviation network and node attack comparison. Journal of Systems Engineering. 2013(1):1–7.
90. Buldyrev SV, Roni P, Gerald P, et al. Catastrophic cascade of failures in interdependent networks. Nature. 2010;464:1025–1028.