The limitation of the probability of any fatigue failure in a fleet of N fatigue-prone aircraft (FFPN) and fatigue failure rate (FFR) of airline (AL) is a problem of high priority. The offered solution of the problem is based on the acceptance full-scale fatigue test of an aircraft structure. If the result of this test is not good enough then this new type of aircraft will not be used in a service. Previously the redesign of this project should be done. For this strategy there are a maximum of FFPN and a maximum of FFR as functions of unknown parameters of a fatigue life distribution and of a model of fatigue crack growth. In this paper the approach is discussed which allows to limit these maximums for any unknown parameters of fatigue life and fatigue crack model. Numerical examples are given.

Keywords: inspection program, markov chain, monte-carlo, reliability, p-set function, weibull distributions.

FFR, fatigue failure rate; FFPN, fleet of n fatigue-prone aircraft; AL, airline; AC, aircraft; SL, safe life; FS, fail safe; DT, damage tolerance; MIMAR, modeling in industrial maintenance and reliability; CDF, cumulative distribution functions; RV, random variable; ML, maximum likelihood; MCh, markov chain; CD, crack detection; FF, fatigue failure.

This paper is in some way a review, a correction and a development of our previous publications devoted to an elimination of a fatigue failure of an aircraft (AC). We discuss here the economical effectiveness of an airline (AL) under a limitation of the fatigue failure rate (FFR) and the limitation of any fatigue failure probability in a fleet of N fatigue-prone aircraft (FFPN).

 The study of the fatigue problem of the aircraft has a long history. The earliest reported accident was the wing failure of a Dornier Merkur on 23 september 1927.¹ C Torkingtion² in his paper reminds: “In a two year period from 1942, about 20 Vickers Wellington bombers were lost in the UK as a result of fatigue failures of the wing main spar joints. In the war situation, if 20 failures in the UK were identified as fatigue, one can only guess that at least a similar number were lost over the sea or enemy territory”.

The most significant accidents were the catastrophic failures of Comet (1953, 1954), Fokker F-27 (1968), F-111 (1969), Hawker Siddeley (1976) and Boeing - 707 - 321C (1977). The most massive structural failure ever survived by an airliner was a geriatric (89,000 - flight) failure of B - 737 (1988). The details of these milestone case histories in aircraft structural integrity are described in.³ And at least hitherto the problem of elimination of fatigue failure is not solved . For example, at the beginning of 2012 year fatigue cracks was discovered in the in the wings of two А380 (4 years of service in Singarope Airlines).

The crash of three Comets was the most significant event, which has a very strong influence on the next aircraft airframe development. Special philosophy and system of aircraft development should have been created in order to prevent aircraft fatigue failure. The first main ideas of the system were offered just during the Comet inquiry⁴ in October - November 1954. Much attention was paid to the scatter of fatigue life. This is the opinion of director of the Royal Aircraft Establishment: ".... I would have the whole aeroplane tests carried on until the next failure took place, and then take half a dozen specimens and get a safety life, we would then put variation as 3:1 on either side of the average. Whereas, if you only work on a single specimen, you would have to give a safety life of about one ninth of what the specimen comes to, because the specimen might by chance have been the strongest...".⁴ The approach to the fatigue problem, which developed from these ideas, was called a Safe-Life (SL) approach. Basically this requires that all the parts of the structure, the failure of which could result in loss of the aircraft, are to be able to remain safely in use for a predetermined retirement life (specified life (SL)).

The developed country like USA, introduced Fail-Safe Concept (FS) for fixed wing transport aircraft was later would serve as the framework for common international standards. This new standard resulted from the US. FAA Transport Category Airplane Fatigue Regulatory Review Conference held in March, 1977.⁵ The European position, primarily advocated by the United Kingdom, was that transport category aircraft should meet two standards, the fail-safe and the safe-life methods, for certification of fixed wing aircraft.

Later the USAF provided new guidelines: Damage Tolerance (DT) philosophy.⁶ This philosophy is in many ways similar to the fail-safe approach but it goes somewhat further in that consideration is given to crack growth from flaws which may be present in the structure as manufactured. Such flaws may arise from inherent metallurgical imperfections in the material used, or from manufacturing imperfections. The damage tolerance evaluation of structure is intended to insure that should serious fatigue cracks or damage occur, the remaining structure can withstand reasonable loads without excessive structural deformations until the damage is detected.

The FS and the DT concepts make emphasis on the design and test. During fail-safe test we have to prove, that the requirements are met. But it should be taken into account that even if the requirements are met the "fail-safe" structure is not safe, if it is not timely inspected and repaired. “So far better title would be "inspection dependent". This clearly puts the emphasis for safety on the inspector, and implies that, without inspection, things may well be dangerous".⁷

For the choice of the SL and the program of inspections for the FS and the SL methods correspondingly, several mathematical problems should be solved. The model of fatigue crack growth should be developed and the cumulative distribution function of fatigue life should be studied. The mathematics for the calculation of the probability of the fatigue crack detection should be developed also. There is a lot of publications devoted to these problems. We mention only the most significant ones.

Much attention to these problems was devoted in the papers of Yang JN, et al.^8-16 The statistical crack growth model and the distribution on equivalent initial flaw size were studied in.^14,15 The models of fatigue crack are offered also in^17,18 and.^16,19 In two last papers the process of the fatigue crack growth is considered as random process.

Statistical estimation of economic life for aircraft structures and aircraft fleet maintenance based on structural reliability analysis was studied in.^13,20,21 Some state-of-the-art and new mathematical approach to the problem was presented in 8^th IMA International Conference on Modelling in Industrial Maintenance and Reliability (MIMAR), Oxford, Institute of Mathematics and its Applications, 2014. In²² the control limit policy for aging systems using Markov decision process, in²³ a cooperative game-based decision method for aircraft fleet maintenance are discussed. Minimax approach to the development of inspection program in order to provide the economical effectiveness of an airline (AL) under a limitation of the fatigue failure rate (FFR) and the limitation of any fatigue failure probability in a fleet of N fatigue-prone aircraft (FFPN) is offered in.²⁴ The theory of semi-Markov process with rewords was used for the solution of these problems.

Usually, the reliability problem is considered as a problem of the probability theory when the cumulative distribution functions (CDFs) of corresponding random variables (a fatigue life, fatigue crack model parameters …) are known already. But in this paper, which is the development of²⁴ and some solutions presented in,²⁵ the main attention is devoted to the statistical problems when these CDFs are not known but thesolution of the problem is based on the acceptance full-scale fatigue test of an aircraft structure. In Appendix A the planning of inspection intervals is considered as definition of some set of specific “prediction intervals” for “future observations” (the detection and the fatigue failure times of the fleet aircraft) based on the processing of the acceptance fatigue test. After this test one of the two decisions should be chosen: 1) to do the redesign of new type of AC if the result of the test is “too bad” or 2) make the development of inspection program in other case. In this case required reliability can be provided for any unknown parameter of fatigue crack growth. Special attention in this paper will be made also to the beginning of service of a fleet of a new type aircraft.

 There are two versions of the problem.

1. The nomination of the specified life as some value in the interval$(0,\infty )$ .
2. The SL is already nominated but it is necessary to check the required reliability.

Estimate of specified life

Usually for fatigue life data processing both lognormal and Weibull distributions are used. If we use logarithm scale (if we use $X=\ln (T)$  instead of random variable (RV) T), both these distributions will become distributions with location and scale parameters

$X={\theta }_0+{\theta }_1\stackrel{0}{X},$                        (1)

where ${\theta }_0,{\theta }_1$  are unknown parameters, RV $\stackrel{0}{X}$  has either cdf $F\stackrel{0}{X}(x)=\Phi (x)$ , where $\Phi (x)$ is cdf of standard normal or the standard smallest extreme value (sev), $F\stackrel{0}{X}(x)=1-\exp (-\exp (x))$ , distributions (for lognormal or Weibull distributions of T correspondingly). In following we use logarithm scale.

 Let $X=(X_1,\mathrm{...},X_n)$  where$X_i,i=1,\mathrm{...},n$ , is the fatigue life of AC (it is a random variable) in full-scale fatigue test, $Y=(Y_1,\mathrm{...},Y_N)$ , $Z=\min (Y_1,\mathrm{...},Y_N)$  where$Y_j,j=1,\mathrm{...},N$ , is the fatigue life (random variable) of AC in service. We consider the case when all components of vectors X and Y are independent RVs with the same cdf which has the location and scale parameters

$F\stackrel{0}{X}((x-{\theta }_0)/{\theta }_1)$ , $i=1,\mathrm{...},n$ , $j=1,\mathrm{...},N$ .

In order to limit the probability of fatigue failure of any AC in service by small value

$\epsilon$  the SL, $\tau =\tau (X)$ , should be found from the equation

${\sup }_{\theta }P(Z\le \tau (X))\le \epsilon$ .          (2)

For considered assumptions we have the following solution ²⁵

$\widehat{\tau }={\widehat{\theta }}_0+t_1{\widehat{\theta }}_1$                                (3)

where the random variables, estimates of ${\theta }_0,{\theta }_1$  (for example, estimates of Maximum Likelihood (ML) method) as function of $X=(X_1,X_2,\mathrm{...},X_n)$  have the following structures

${\widehat{\theta }}_0={\theta }_0+{\theta }_1{\stackrel{o}{\theta }}_0,{\widehat{\theta }}_1={\theta }_1{\stackrel{o}{\theta }}_1,$   (4)

where ${\stackrel{o}{\theta }}_0,{\stackrel{o}{\theta }}_1$  are RVs corresponding to the estimates of ${\theta }_0,{\theta }_1$  using a sample $\stackrel{0}{X}=({\stackrel{0}{X}}_1,\mathrm{...},{\stackrel{0}{X}}_n)$  of the same size n but when ${\theta }_0=0,{\theta }_1 =1$ ;the RV $\stackrel{0}{Z}$  has the same type of CDF as Z but ${\theta }_0=0,{\theta }_1 =1$ ; t₁is $\epsilon$ -quintile of RV $V_Z=(\stackrel{0}{Z}-{\stackrel{0}{\theta }}_0)/{\stackrel{0}{\theta }}_1$  , $\epsilon$  is allowed probability of failure of any AC.

Fixed required specified life-test time limitation

Now we consider the case when the required SL,$\tau$ , is fixed already but using result of the acceptance full-scale fatigue test it is necessary to check the reliability requirement. And we consider also definition of the required test time.

 Let us define

$\widehat{\tau }={\widehat{\theta }}_0+t_2{\widehat{\theta }}_1$          (5)

and we say that required reliability is provided if $\widehat{\tau }>\tau$ . The value t₂ we should define in such a way that probability of acceptance of the test and probability of fatigue failure of any AC in service should be limited for any parameter $\theta$  by very small value, $\epsilon$

$P(Z<\tau {\displaystyle \cap \widehat{\tau }}>\tau )\le \epsilon$ .             (7)

It can be shown [see²⁵) that t₂ is the solution of the equation (8)

$\underset{\text{C}}{\text{sup}}F{}_{{}_{\stackrel{O}{Z}}}(c)F_{V_C}(t_2)=\epsilon$       (8)

where RV

${\text{V}}_{\text{C}}=(c-\stackrel{0}{{\displaystyle {\theta }_0}})/{\stackrel{0}{{\displaystyle \theta }}}_1.$

It is worth to note that if the test of all n ACs are made simultaneously, the defined by (4) structure of the parameter estimates takes place only if the test will be stopped at the moment of k^th failure, $k=2,\mathrm{...},n$ . The value of k can be chosen taking into account some specific economical reason. Special attention should be made for the case when the scale parameter, ${\theta }_1$ , is known. In this case it can be found the limitation of the test time without any failure. It can be shown that in this case the required SL, $\tau$ , can be excepted and required reliability $(1-\epsilon )$  will be provided if the smallest fatigue life of the tested AC will be more than $x_{(1)}=\tau -t_2^1{\theta }_1$  where $t_2^1$  is the solution of the equation

$\underset{C}{\max }F{}_{\stackrel{0}{Z}}(c){(1-F_{\stackrel{\circ }{X}}(c-t_2^1))}^n=\epsilon .$         (9)

Numerical examples of the test time nomination ,/

Simultaneously fatigue tests of 6 airframes of the same type of aircraft have been made but only up to 4^th fatigue failure. So we know only 4 first minimal fatigue lives: (t₍₁₎, ..., t₍₄₎)=(59971; 72600; 77630; 80863) and correspondingly for x(i) = ln( t(i)), i=1,...4, we know x =(x₍₁₎, ..., x₍₄₎) = (11.002; 11.193; 11.260, 11.3005). There are 100 aircraft in operation and there is a requirement, that the probability of at least one fatigue failure before $t_{SL}=50000$  cycles should not exceed p = 0.05. Then$\tau =log\left(50000\right)=10.82$ . We can be sure of the required reliability if ${\widehat{\theta }}_0+t_2{\widehat{\theta }}_1>\tau .$

Let us consider the lognormal distribution of the fatigue life. Then using the Lifereg procedure of SAS system we can easily get ML estimates${\widehat{\theta }}_0=11.26,{\widehat{\theta }}_1=0.145$ . And then using Monte Carlo method to get the cdf of RV VC (5000 samples) we have, that t₂= -7.055 is the root of the equation

$\max (1-{(1-\Phi (c))}^m)F{}_{V_C}(t)=p=0.05$             (10)

Where

$V_C=(c-{\stackrel{0}{\theta }}_0)/\stackrel{0}{{\theta }_1}$ .

Accordingly${\widehat{\tau }}_2={\widehat{\theta }}_0+t_2{\widehat{\theta }}_1=11.26-7.055*0.145=10.237$ . This value is less than required $\tau =\mathrm{10.82.}$  So the required reliability is not provided. Now let us consider the case when ${\theta }_1=0.346$  is known and a new fatigue test after some structure retrofit has to be made. And we have to know the time limit of the fatigue test without any failure, which will be enough to be sure of the required reliability. In this case $t_2^1=-2.04$  is the root of the equation

$\underset{c}{\max }(1-{(1-\Phi (c))}^N){(1-\Phi (c-t))}^n=0.05,N=100;n=6.$       (11)

So for the required time limit of the fatigue test without the failure (in logarithm scale) we have

$x_{WF}=x_{(1)}=\tau -t_2^1{\theta }_1=10.82-(-2.0425)\times 0.346=11.52648$

or in the natural scale

$t_{WF}=\exp (11.52648)=101365$ .

It is worth to note that for the same initial data but for Weibull distributions of fatigue live the required time of test without failure is equal to 179836.

Limitation of fatigue failure rate

 Now we suppose that reliability of every AC is defined by fatigue crack which is discovered with probability 1 if inspection is made in the interval $(T_d,T_c)$ where $T_d,T_c$  are random variables: $T_d$  is the time when the fatigue crack can be detected, $T_c$  is the time when the fatigue failure takes place. Here we consider the simplest case: interval between the inspections is equal to the constant $t_{SL}/(n+1)$  , where $t_{SL}$ is the aircraft specified life (SL) (the retirement time). The process of an operation of AL can be considered as a Markov chain (MCh)²⁵ with $\left(n+4\right)$ states. The states $E_1,E_2,\dots ,E_{n+1}$  correspond to an AC operation in the time intervals$\left[t_0,t_1\right),\left[t_1,t_2\right),\dots ,\left[t_n,t_{n+1}\right),t_0=0,t_{n+1}=t_{SL}$ . The states$E_{n+2}$ , $E_{n+3}$  and $E_{n+4}$  correspond to the events: AC reaches the SL without any problem, the fatigue failure (FF) or the fatigue crack detection (CD) take place and in all these three cases the new AC is purchased and begins the service in first interval.

In the corresponding transition probability matrix, P_AL, let ${\nu }_i$  be the probability of a crack detection during the inspection number i , let $q_i$  be the probability of the failure in service time interval $\left(t_{i-1},t_i\right]$ , and let $u_i=1-{\nu }_i-q_i$  be the probability of successful transition to the next state. In our model we also assume that an aircraft is discarded from a service at $t_{SL}$  even if there is no any crack discovered by inspection at the time moment$t_{SL}$ .

The inspection at the end of $\left(n+1\right)$ -th interval (in state $E_{n+1}$ ) does not change the reliability but it is made in order to know the state of aircraft (whether there is a fatigue crack or there is no fatigue crack). It can be shown that$u_i=P(T_d>t_i|T_d>t_{i-1})$ , $q_i=P(t_{i-1}<T_d<T_c<t_i|T_d>t_{i-1})$ , ${\nu }_i=1-u_i-q_i$ , $i=1,\dots ,n+1$ . In the three last lines of the matrix P_AL there are three units in the in the first column. All the other entries of this matrix are equal to zero, see Table 1.

Using the theory of the semi-Markov process with rewards and the definition of the matrix P_AL we can get the vector of stationary probabilities,$\pi =({\pi }_1,\mathrm{...},{\pi }_{n+4})$ , which is defined by the equation system:

$\pi P_{AL}=\pi ,{\displaystyle \sum _{i=1}^{n+4}{\pi }_i=1}$                                 (12)

and the airline gain

$g\left(n\right)={\displaystyle \sum _{i=1}^{n+4}{\pi }_i{g}_i\left(n\right)}$                (12a)

where

$g_i\left(n\right)=\{\begin{array}{c}{a}_i{u}_i+b_i{q}_i+c_i{\nu }_i, i=1,\dots ,n+1,\\ d_i, i=n+2,\dots ,n+4,\end{array}$ .

a_i is the reward defined by the successful transition from one operation interval to the following one and the cost of one inspection; b_i, c_i and d_i correspond to transition to the states $E_{n+3}$  (FF), $E_{n+4}$  (CD) and then to the state $E_1$  (the “cost” of FF of AC, fatigue crack detection, acquisition of new AC) . Let us note that if$a_i=t_i-t_{i-1},b=c=d=0$  then

$g\left(n\right)={\displaystyle \sum _{i=1}^{n+4}{\pi }_i{g}_i\left(n\right)=g_t\left(n\right)={\displaystyle \sum }_{i=1}^{n+1}{\pi }_i(t_i-t_{i-1})}$  .             (13)

Let the cdf of the vector ($T_d,T_c$ ) and the matrix $P_{AL}$ are defined by the known parameter$\theta$ . Then we should consider $g(n,\theta )$  and $g_t(n,\theta )$ . The value $L_j=g_t(n,\theta )/{\pi }_j$  defines the mean time to return to the same state$E_j$ . So ${\lambda }_F(n,\theta )=1/L_{n+3}$  is the FFR.

If $\theta$ is known we calculate the gain as a function of$n,g(n,\theta )$ , and choose the number $n_g$  corresponding to the maximum of gain : $n_g(\theta )=\arg \underset{n}{\max }g\left(n,\theta \right)$ . Then we calculate FFR as function of $n,{\lambda }_F(n,\theta )$ , and choose $n_{\lambda }$  in such a way that for any $n\ge n_{\lambda }$  the function ${\lambda }_F(n,\theta )$  will be equal or less than some value$\lambda :n_{\lambda }(\lambda ,\theta )=\min \left\{n:{\lambda }_F(n,\theta )\le \lambda ,\text{ for all }n\ge n_{\lambda }(\lambda ,\theta )\right\}$ . And finally$n=n_{g\lambda }(\lambda ,\theta )=\max (n_g,n_{\lambda })$ , Figure 1.

Figure 1 The choice of inspection number$n=n_{g\lambda }(\lambda ,\theta )=\max (n_g,n_{\lambda })$ .

 But if $\theta$ is not known the value n is a $RV:\widehat{n}=n_{g\lambda }(\lambda ,\widehat{\theta })$ . For the approximate solution the confidence interval for the $\theta$  can be used. But some uncertainty appears: confidence level is not defined by required reliability. The precise solution of the limiting value $\lambda$  can be found in case if the fatigue test is acceptance test. The result of acceptance test can be used to calculate the estimate of the parameter$\theta ,\widehat{\theta }=\widehat{\theta }(x_1,\mathrm{...},x_n)$ . The service of a new type of aircraft will not take place if the result of the fatigue test in a laboratory is “too bad” (previously, the redesign of the new type of AC should be made). We say that in this case the event $\widehat{\theta }\notin {\Theta }_0$  takes place, where${\Theta }_0\subset \Theta ,\Theta$  is a parameter space (for example, $\widehat{\theta }\notin {\Theta }_0$  if the test fatigue life, t_C, is lower than some limit; or $n_{g\lambda }(\lambda ,\widehat{\theta })$  is too large,…).

Let ${\lambda }_{FD}$  be a preliminary designed allowed FFR which is the solution of the equation

${\sup }_{\theta }{E}^{\widehat{\theta }}({\lambda }_F(n_{g\lambda }({\lambda }_{FD},\widehat{\theta }),\theta )|\widehat{\theta }\in {\Theta }_0)P\left(\widehat{\theta }\in {\Theta }_0\right))=\lambda$                       (14)

where $E^{\widehat{\theta }}(.)$  is the expectation corresponding to the distribution of $\widehat{\theta }$  under condition $\widehat{\theta }\in {\Theta }_0$ .

Then the number of inspections $n_{g\lambda }({\lambda }_{FD},\widehat{\theta })$  provides the limitation of $\lambda$  independently of any unknown parameter $\theta$ .

Limitation of probability of any fatigue failure in fleet of aircraft

Now we consider the case when the operation of all N aircraft will be stopped if any fatigue crack will be detected. So in order to limit the probability of fatigue failure in the fleet (FFPN) it is enough to find at least one fatigue crack before the failure of any aircraft in the fleet takes place. Let $t_k^{+},t_{k-1}^{+}<t_k^{+},t_0^{+}=0$  to be “calendar” time moment when k^th aircraft begins the service, $T_{d_k}^{+}=t_k^{+}+T_{d_k},T_{c_k}^{+}=t_k^{+}+T_{c_k},\text{ k}=1,2,\mathrm{...},N$ , to be the random calendar time moments when fatigue crack can be discovered and fatigue failure of AC takes place correspondingly, see Figure 2. And let $K_{SL}=\{k:T_{ck}<t_{SL},k=1,2,\mathrm{...},N\}$  be a set of an indexes of aircraft the failure of which can take a place if an inspection will not take the place, $T_f^{+}=\min \{T_{ck}^{+}:k\in K_{SL}\}$ , is a calendar time corresponding the first failure in the fleet without inspections and let $K_f=\left\{k:1\le k\le N,t_{0k}^{+}<T_f^{+}\right\}$  is the set of aircraft the service of which begin before the first failure in the fleet, $K_{SLf}=K_{SL}{\displaystyle \cap K_f}$ ; and let us define:
$T_{dkf}^{+}=\min \{T_{dk}^{+},T_f^{+}\},$ $T_{ckf}^{+}=\min \{T_{ck}^{+},T_f^{+}\},$ $R_{dkf}=\max \left\{j:t_{kj}^{+}<T_{dkf}^{+},j=0,1,2,\mathrm{...}\right\}$ , $R_{ckf}=\max \left\{j:t_{kj}^{+}<T_{ckf}^{+},j=0,1,2,\mathrm{...}\right\}$ , $R_{kf}=R_{ckf}-R_{dkf}$ where $k\in K_{SLf}$ .
For fixed value of parameter $\theta$  the probability of any failure in the fleet$p_{fNW}(n,\theta )$  will be equal to expected value of random variable $P_{fNW}(n,\theta )$

$p_{fNW}(n,\theta )=E^T(P_{fNW}(n,\theta ))$ .               (15)

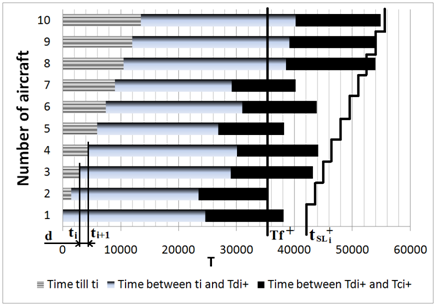
Figure 2 Inspection of N aircraft.

where

$$P_{fNW}(n,\theta )=\{\begin{array}{l}{P}_{f1W},\text{ if }w=1,\\ (1-w){}^{R_f},\text{ if 0}\le w<1,\end{array}{P}_{f1W}=\{\begin{array}{l}1,\text{ if }{R}_f=0\text{, }\\ 0\text{, if }{R}_f\ge 1\end{array}$$  

w is a human factor: a probability, that the planned inspection will be made, $R_f={\displaystyle \sum _{k\in K_f}{R}_{kf}}$  is the total random number of inspections before the first failure in the whole fleet; $E^T(.)$  is the expectation corresponding to the distribution of a set of vectors $({(T_D^{+},T_C^{+})}_k,k=1,\mathrm{...},N)$ . Let us note that if $w=1$  but the expected probability is very small then approximately

$E(P_{fNW}(n,\theta ))=E(1-{\displaystyle \prod _{k=1}^N(1-}{P}_{f1Wk}))\approx E({\displaystyle \sum _{k=1}^N{P}_{f1Wk})}$ .        ( 15a )

The necessary calculation can be made by the use of Monte Carlo method taking into account the distribution of random variables T_d and T_c . If parameter $\theta$ is known then the number of the inspections, $n(p,\theta )$ , required to limit the FFPN by a value p, is defined by the equation

$n(p,\theta )=\min (r:p_{fNW}(\theta ,r)\le p\text{ for all }r>n(p,\theta ),r=1,2,\mathrm{...})$ .       (16)
For the case of using the result of the acceptance test for the estimation of the parameter $\theta$  the required limitation of the FFPN by a value p is provided for any unknown $\theta$  if the number of the inspections will be defined by value $n(p_{FD},\widehat{\theta })$ , where $p_{FD}$  is the solution of the equation

$\underset{\theta }{\sup }{E}^{\widehat{\theta }}\{E^T(P_{fNW}(n(p_{FD},\widehat{\theta }))|\widehat{\theta }\in {\Theta }_0)\}P(\widehat{\theta }\in {\Theta }_0)=p$                         (17)

where again $E^T(.)$  is the expectation corresponding to the distribution of a set of vectors $({(T_D^{+},T_C^{+})}_k,k=1,\mathrm{...},N)$ , the $E^{\widehat{\theta }}(.)$  is the expectation corresponding to the distribution of $\widehat{\theta }$  under condition $\widehat{\theta }\in {\Theta }_0$ .

We suppose that the equation$a(t)=\alpha \exp (Qt)$ , where $\alpha$  is some constant, Q is some RV, describes the development of fatigue crack in the interval, (t_d, t_c) where t_d is a time when the crack becomes detectable $\left(a(t_d)=a_d\right)$  and t_c is a time when the crack reaches its critical size $\left(a(t_c)=a_c\right)$  and fatigue failure takes place. Corresponding random variables are defined by equations: $T_d=(\log a_d-\log \alpha )/Q=C_d/Q$ , $T_c=(\log a_c-\log \alpha )/Q=C_c/Q$ .

Let us denote $X=\log Q$  and$Y=\log C_c$ , where $C_c=\log a_c-\log \alpha$ . Here we assume that C_c is some constant. From the analysis of the fatigue test data it can be assumed, that the$\log T_c=\log C_c-\log Q$ is distributed normally. It can take place only if $X=\log Q$  has normal distribution. Additionally we assume that standard deviation of log(Q) is equal to 0.346.

Now we consider an example of the problem to limit the FFPN by the value p=0.05. Suppose that during fatigue test we see the fatigue crack (see Figure 2.22 in ¹ ) and get the following data:

 $\log (Q)=-8.588$ ; $\alpha =0.286mm$ . It is known: ${\alpha }_d=20mm, {\alpha }_c=237mm$ ¹. Assume that $t_{SL}=40000h,w=0.9$ ; there is 10 aircraft in the fleet, the interval between the aircraft putting into operation as$t_{i+1}-t_i=500h$ ; required reliability $R=0.95$ , allowed failure probability $\epsilon =1-R=0.05$ , a number of allowed maximal inspections is equal to 20 (the redesign of aircraft should be made if required reliability $R=0.95$ is provided only for the inspection number, $\widehat{n}=n(\epsilon ,\widehat{\theta })$  , more than 20; this requirement defines the set ${\Theta }_0$ .

 The calculations made by the use of Monte Carlo method show: if ${\theta }_0=\log (Q)=-8.588$ , ${\theta }_1=0346$  are fixed, all inspection intervals are equal, then it can be calculated that 9 inspections for each aircraft during the operating time should be carry out to ensure the required reliability. But if it taken into account that${\theta }_0=\log (Q)=-8.588$  is only the estimate of the unknown parameter then 16 inspections should be chosen corresponding to$p_{FD}=0.01$ . We see that in order to limit the fleet failure probability for any unknown ${\theta }_0$  by the value $\epsilon =0.05$  the inspection interval should be calculated using $p_{FD}=0.01$ .

Appendix A

Here we consider only the limitation of any fatigue failure in a fleet of N aircraft and show a connection of the development of the inspection program with the definition of a prediction interval for future observation.²⁶

Let $Z=(Z_1^{+},\mathrm{...},Z_N^{+}\}$ , where $Z_k^{+}=(T_{d,k}^{+},T_{c,k}^{+}),k=1,\mathrm{...},N$  are some previously defined vectors, the vector X defines the result of the acceptance full-scale fatigue test of an aircraft structure. It is supposed that the class is known$\{P_{\theta },\theta \in \Theta \}$  to which the probability distribution of the random vector W=(Z, X) is assumed to belong. Of the parameter$\theta$ , which labels the distribution, it is presumably known only that it lies in a certain set $\Theta$ , the parameter space and $\widehat{\theta }$  is the estimate of the parameter $\theta$  as a result of processing X. It is useful to note that the choice of the program with the n inspections defines some random set function

$S^{+}(\widehat{\theta },{\Theta }_0,n)={\displaystyle {\cup }_{1\le k\le N}{S}_k^{+}}(\widehat{\theta },{\Theta }_0,n)$                      (A1)

where

$S_k^{+}(\widehat{\theta },{\Theta }_0,n)=\{\begin{array}{l}{\displaystyle \underset{1\le k\le N}{\cup }{S}_{j,k}^{+}(n)}\text{, }if\widehat{\theta }\in {\Theta }_0,\\ \varnothing ,if\widehat{\theta }\notin {\Theta }_0,\end{array}$
$S_{j,k}^{+}=\{(t_{d,k}^{+},t_{c,k}^{+}):t_{(j-1),k}<t_{d,k},t_{c,k}\le t_{j,k}\},i=1,\mathrm{...},n+1,1\le k\le N$ .

Example of $S^{+}(\widehat{\theta },{\Theta }_0,n)$  is shown in Figure 3.

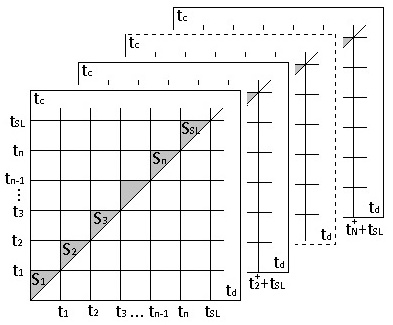
Figure 3 Example of$S^{+}(\widehat{\theta },{\Theta }_0,n)$ .

This function defines some set of specific “prediction intervals” for the set of the vectors $\{Z_k^{+},k=1,\mathrm{...},N\}$  based on the observation of the X (or based on the estimate $\widehat{\theta }$  of the parameter $\theta$ ) which defines the probability of any fatigue failure in the fleet , FFPN. We remind that if X is the result of the acceptance test the required limitation of the FFPN by a value p is provided for any unknown $\theta$  if the number of the inspections will be defined by value $n(p_{FD},\widehat{\theta })$ , where (we remind) $p_{FD}$  is the solution of the equation

$\underset{\theta }{\sup }{E}^{\widehat{\theta }}\{E^T(P_{fNW}(n(p_{FD},\widehat{\theta }))|\widehat{\theta }\in {\Theta }_0)\}P(\widehat{\theta }\in {\Theta }_0)=p$                         (A2)

where again $E^T(.)$  is the expectation corresponding to the distribution of a set of vectors $({(T_D^{+},T_C^{+})}_k,k=1,\mathrm{...},N)$ , the $E^{\widehat{\theta }}(.)$  is the expectation corresponding to the distribution of $\widehat{\theta }$  under condition $\widehat{\theta }\in {\Theta }_0$ .

Some details can be provided if the human factor w=1. It can be shown that in this case for a very broad spectrum of set ${\Theta }_0$  there is a preliminary “designed” choice of allowed FFPN, $p_{FD}$ , such that

${\sup }_{\theta }P\{{\displaystyle \underset{k=1}{\overset{N}{\cup }}{\displaystyle \underset{j=1}{\overset{n}{\cup }}(Z_k^{+}\in S_{j,k}^{+}(n(p_{FD},\widehat{\theta })))|\widehat{\theta }\in {\Theta }_0\}P(\widehat{\theta }\in {\Theta }_0)=p}}$  .         (A3)

If additionally, the services of all aircraft are independent (after discovery of fatigue crack the service of only one corresponding aircraft will finished but the service of all other aircraft continues) than again there is the “preliminary designed” choice of $p_{FD}$  such that

${\sup }_{\theta }(\{1-{\displaystyle \prod _{k=1}^N(1-{\displaystyle {\sum }_{1\le j\le n}P(Z_k^{+}\in S_{j,k}^{+}(n(p_{FD},\widehat{\theta }))|\widehat{\theta }\in {\Theta }_0\}P(\widehat{\theta }\in {\Theta }_0)}}=p$ .     (A4)

If the left side part of (A4) is small enough then instead of (A4) the equation (A5) can be used

${\sup }_{\theta }\left\{{\displaystyle \sum _{k=1}^N{\displaystyle {\sum }_{1\le j\le n}P(Z_k^{+}\in S_{j,k}^{+}(n(p_{FD},\widehat{\theta })){\displaystyle \cap \widehat{\theta }\in {\Theta }_0})}}\right\}=p$ .                                  (A5)

Note: It should be noted that in [27] similar problem was considered but with some mistakes. The equation (A2) is not given at all but the equation (A5) is given without explanation that it can be used only if p is very small.

Equations (A2 – A5) show that the FFPN will be limited by the value p for any unknown parameter$\theta$ .

Some mathematics for the solution of the problem of the limitation of the probability of any fatigue failure in a fleet of N fatigue-prone aircraft (FFPN) and fatigue failure rate (FFR) of some airline is offered. Usually, the reliability problem is considered as a problem of the theory of probability when the cumulative distribution functions (CDFs) of the corresponding random variables (the fatigue life, the fatigue crack model parameters …) are known already. But in this paper the main attention is devoted to the statistical problem when these CDFs are not known but thesolution of the problem is based on the acceptance full-scale fatigue test of an aircraft structure. In the Appendix A the planning of inspection intervals is considered as definition of some set of specific “prediction intervals” for “the future observations” (the detection and the fatigue failure times of the fleet aircraft). They are based on the processing of the acceptance fatigue test. After this test one of the two decisions should be chosen: 1) to do the redesign of new type of AC if the result of the test is “too bad” or 2) to make the choice of the number of inspection, $n=n(\widehat{\theta },p_{FD})$ , as function of $\widehat{\theta }$  and specific $p_{FD}$  defined in this paper. In this case required reliability can be provided for any unknown parameter of fatigue crack growth.

None.

Author declares that there is no conflict of interest.

1. Campbell GS, Lahey RA. Survey of Serious Aircraft Accidents Involving Fatigue Fracture. Int J Fatigue. 1984;6(1):25‒30.
2. Torkington C. Fatigue Problems Old and New. Aircraft. 1980;59(10):8‒11.
3. Wanhill RJH. Milestone Case Histories in Aircraft Structural Integrity. National Aerospace Laboratory NLR, Netherlands; 2002. p. 521‒525.
4. The Comet Inquiry. Flight. 29 October, 1954; 638‒639, 652‒654; 5 November, 1954; 725‒728; 19 November, 1954; 731‒732, 740‒742; 26 November, 1954; 787‒789.
5. US Sets Pattern for Fatigue Standards. Aviation Week and Space Technology. March 28, 1977, 32.
6. Hall J, UG Goranson. Structural Damage Tolerance of Commercial Jet Transports. Reprints from 1984 Boeing AIRLINER. Part 1, Damage Tolerance Concepts. Jan-Mar, 1984; part 2, 727 / 737 / 747 Supplement Structural Inspection Programs Apr-June, 1984; part 3 “ 757/767 Structural Inspection Program. July-Sep, 1984.
7. Heath WG. Fail Safe Tech. Air.1979.
8. Yang JN, Trapp WJ. Reliability Analysis of Aircraft Structures under Random Loading and Periodic Inspection. AIAA Journal. 1974;12(12):1623‒1630.
9. Yang JN, Trapp WJ. Inspection Frequency Optimization for Aircraft Structures Based on Reliability Analysis. Journal of Aircraft. 1975;12(5):494‒496.
10. Yang JN. Reliability Analysis of Structures Under Periodic Proof Tests in Service. AIAA Journal. 1976;14(9):1225‒1234.
11. Yang JN. Optimal Periodic Proof Test Based on Cost-Effective and Reliability Criteria. AIAA/ASME/SAE 17th Structures, Structural Dynamics and Materials Conference Proceedings. Pennsylvania; 1976. p. 567‒576.
12. Yang JN, Trapp WJ. Joint Aircraft Loading/Structure Statistics of Time to Service Crack Initiation. Journal of Aircraft 1976;13(4):270‒278.
13. Yang JN. Statistical Estimation of Economic Life for Aircraft Structures. Journal of Aircraft. 1980;17(7):528‒535.
14. Yang JN. Statistical Crack Growth in Durability and Damage Tolerant Analysis. In: AIAA/ASME/ASCE/AHS. 22nd Structures, Structural Dynamics and Materials Conference Proceedings. USA, 1980. p. 38‒44.
15. Yang JN, Manning SD. Distribution on Equivalent Initial Flaw Size. In: Proceedings of Annual Reliability and Maintainability Symposium. San Francisco, California, US; 1980. p. 112‒120.
16. Yang JN, Manning SD. Aircraft Fleet Maintenance Based on Structural Reliability Analysis. Journal of Aircraft. 1994;31(2):419‒425.
17. Mohanty JR, Verma BB, Ray PK. Prediction of Fatigue Crack Growth and Residual Life Using an Exponential Model: Part I (constant amplitude loading). Intemational Journal of Fatigue. 2009;31(3):418‒424.
18. Mohanty JR, Verma BB, Ray PK. Prediction of Fatigue Crack Growth and Residual Life Using an Exponential Model: Part II (mode-I overload induced retardation). International Journal of Fatigue. 2009;31(3):425‒432.
19. Spencer BF, J Tang. Markov Process Model for Fatigue Crack Growth. Journal of Engineering Mechanics. 1988;114(12):2134‒2157.
20. Silvar R De. Exponential Model of Fatigue Crack. In Proceeding of the International workshop "Aviation Reliability AvR 2000”, Riga, RAU, Latvia. 2000. p. 45‒48.
21. Aven T, Castro IT. A Delay-Time Model with Safety Constraints. Reliability Engineering & System Safety. 2009;94(2):261‒267.
22. Jin L, Bayarsaikhan U. Control Limit Policy for Aging Systems Using Markov Decision Process. Proceedings for 8th IMA International Conference on Modeling in Industrial Maintenance and Reliability (MIMAR). Oxford, Institute of Mathematics and its Applications, 2014. p. 149‒154.
23. Feng Q, Chen Y, Sun B. A cooperative game-based decision method for aircraft fleet condition based maintenance. Proceedings for 8th IMA International Conference on Modeling in Industrial Maintenance and Reliability (MIMAR). Oxford, Institut of Mathematics and its Applications, 2014. p. 89‒96.
24. Hauka M, S Tretyakov, Yu Paramonov. Minimax inspection program for reliability of aircraft fleet and airline. Proceedings for 8th IMA International Conference on Modeling in Industrial Maintenance and Reliability (MIMAR). Oxford, Institute of Mathematics and its Applications, 2014. p. 120‒124.
25. Paramonov Y, Kuznetsov A, Kleinhofs M. Reliabilty of fatigue-prone airframes and composite materials. Aviation institute of Riga. Technical University, Latvia, 2011. p. 129.
26. Cox DR, Hinkly DV. Theoretical statistics. Chapmen and Hall,London, UK; 1979. p. 528.
27. Paramonov Y, Tretyakov S, Hauka M. Reliability of aircraft fleet: Binary p-set and lambda-set functions. International Journal of Performability Engineering. 2016;12(3):215‒228.