Currently the primary object of airport air quality are the nitrogen oxides and particle matter (PM10, PM2.5 and ultrafine PM) emissions from aircraft engine exhausts as initiators of photochemical smog and regional haze, which may further impact on human health. Analysis of PM emission inventory results at major European airports highlighted on sufficiently high contribution of aircraft engines and APU. The paper aims to describe the method for calculation of emission and dispersion of PM, produced by aircraft engine under operations at the airport. PolEmiCa calculates the distributions of PM fractions for aircraft and APU exhausts. The PM concentration varies inversely proportional to the wind velocity u1 and directly proportional to the vertical component of the turbulent exchange coefficient k1/u1. The evaluation of non-volatile PM concentration includes the size and shape of PM. The maximum concentration of PM in exhaust from APU is higher and appropriate distance is less than in case for gas.

Even through all benefits that airport brings, its activities also contribute to local air quality impact and correspondingly affect the health and quality life of people, living near the airports. Number of flights has increased by 80% between 1990 and 2014 and is forecast to grow by a further 45% between 2014 and 2035. Consequently the future growth in the European aviation sector will be inextricably linked to its environmental sustainability.¹ A lot of studies emphasis on extremely high concentration of toxic compounds (including nitrogen oxides (NOx), particle matter (PM with various sizes: PM₁₀, PM_2.5 and ultrafine), unburned hydrocarbons (UHC) and carbon monoxide (CO)) due to airport-related emissions and their significant impact on the environment^2,3 and health of the people living near the airport.^{4, 5} Considered problems are intensified in connection with increasing air traffic (at a mean annual rate worldwide of about 5%),⁶ rising tensions of expansion of airports and growing cities closer and closer each other and accordingly growing public concern with air quality around the airport.

Currently the primary subject of concern of airport LAQ are the NOx and PM (PM₁₀, PM_2.5) emissions from aircraft engine exhausts, because they are the initiators of photochemical smog and regional haze, which at further steps may impact on human health directly.⁷ Ultrafine particles (UFPs, diameter <100 nm) is of the most concern in recent years, as they are small enough to penetrate deep into the lungs, causing human health damage first of all. The content of UFPs is near to 90% or even more of the total particle number count in areas influenced by vehicle emissions.⁸ Aviation-attributable health impacts due to PM_2.5 will be in 6 times higher in 2025 compared to 2005.⁹ Analysis of inventory emission results at major European (Frankfurt am Main, Heathrow, Zurich and etc.) and Ukrainian airports highlighted that aircraft (during approach, landing, taxi, take-off and initial climb of the aircraft, engine run-ups, etc.) are the dominant source of air pollution in most cases under consideration,^10,11 Figure 1. As shown in Figure 1, the APU contribution to PM emissions is also sufficiently high. APU of the aircraft is a small gas turbine to generate electricity while the main engines are off and to provide bleed air to start the main engines. The paper was focused on the method for calculation of emission and dispersion of PM, produced by aircraft engine under operational conditions at the airport.

Figure 1 The emissions inventory of nitrogen oxides (a) and PM10 (b) within International Boryspol airport with an intensity of takeoffs and landings 50 thousand per year.

In the National Aviation University (Kyiv, Ukraine) a complex model PolEmiCa has been developed,¹² which is based on the Eulerian approach to describe dispersion processes for the matter in atmosphere. Reason for choice of the Eulerian approach (principle difference of PolEmiCa dispersion model from Doc 9889 recommendation to use the Gauss model‒Lagrangian approach) was defined by existing and widely used in USSR previously and in most of the FSU countries currently the national standard OND-86. The complex model PolEmiCa allow to calculate the inventory and dispersion parameters of the aircraft engine emission during the landing-takeoff cycle of the aircraft in airport area.^13‒15

The main model’s equation is based on the solution of the atmospheric diffusion equation for stationary source of emission and air pollution under certain initial and boundary conditions:^16,17

${\displaystyle \sum _{i=1}^2{u}_i}\frac{\partial q}{\partial x_i}={\displaystyle \sum _{i=1}^2\frac{\partial }{\partial x_i}}{k}_i\frac{\partial q}{\partial x_i}+\alpha \times q$     (1)

or for directly defined horizontal and vertical components of the wind velocity and atmosphere turbulence coefficients in a form:

$u\frac{\partial q}{\partial x}+w\frac{\partial q}{\partial z}=\frac{\partial }{\partial y}{k}_y\frac{\partial q}{\partial y}+\frac{\partial }{\partial z}{k}_z\frac{\partial q}{\partial z}+\alpha \times q$    (2)

where i=1,2 for are horizontal and vertical components u and ω of the wind velocity respectively; k_y and k_z are horizontal and vertical components of the atmosphere turbulence coefficient; α is a factor of pollutant transformation; z = 0 corresponds to the level of the underlying ground surface.

For the calculation the pollutant concentration with sufficient accuracy, it is almost enough to adopt, that:^16,17

$u=u_1\frac{\mathrm{lnz}/z_0}{{\mathrm{lnz}}_1/z_0};$      (3)

$K_z=v+k_{1}z/z_{{}_1}$;$K_z=v+k_{1}h/z_{{}_1}$    (4)

$h=\frac{0.05k_1}{{\varpi }_z.z_1}$        (5)

where z₀‒the roughness of the underlying surface, h–height of the surface layer,${\varpi }_z$ - the vertical component of the angular velocity of the Earth.

So, k_z increases linearly with height z in the surface layer z<h and remains constant for z>h. In the case of a surface inversion, according to similarity theory a logarithmic/linear change with z is taken for u, and a linear-fractional change for k_z.

Berlyand^12,16 found analytical solution of the equation (2) to calculate the maximum concentration of harmful substances from point emission source for the case, that the wind speed varies with power law and the coefficient of turbulent diffusion linearly increases:

$u=u_1\times z^n$,$k_z=k_1\times z$       (6)

Thus, the equation (2) was solved by using the analytical method¹⁶ and the assumptions considered above to calculate the maximum volatile (7) and non-volatile (8) PM concentration from point emission source:

$q_m=\frac{0.116\times {(1+n)}^2\times M}{u_1\times H^{1.5\times (1+n)}}\sqrt{\frac{k_1}{k_0{u}_1}}$    (7)

$q_{\omega m}=\frac{0.063\times {(1+n)}^2\times M}{u_1\times H^{1.5\times (1+n)}}\sqrt{\frac{k_1}{k_0{u}_1}}\frac{{\left(1.5+\omega \right)}^{1.5+\omega }}{\Gamma \left(1+\omega \right)e^{\omega }}$    (8)

where u₁–wind velocity and k₁–coefficient of turbulent diffusion at height z₁ both; n–temperature stratification of the atmosphere; M–emission rate; H–height of the emission source; ω–characteristics including the sedimentation rate of non-volatile PM:

$\omega =w/k_1.\left(1+n\right)$    (9)

where w-sedimentation rate, which is calculated according to Stocks law:

$w={\mathrm{1.3.10}}^{-2}.\rho .r^2$     (10)

where ρ–density of non-volatile PM; r–radius of non-volatile PM.

Difference between “volatile” and "non-volatile" is defined by the ratio: w/Um, where: w- sedimentation rate, which is calculated in accordance with the Stokes law (Eq.10); Um–unfavorable wind velocity.

1. if w/u_m ≤0.015, this case corresponds for gases volatile PM
2. if 0.015 ≤w/u_m ≤0.030, this case corresponds for fine PM
3. if w/u_m >0.03, this case corresponds for PM.

Thus, if we know the expected values of wind speed (u), stability of the atmosphere (n) and the value of emission rate (M), it is possible to predict the PM concentration. The dependence of the concentration on mentioned input data is characterized by the same trend for volatile and non-volatile PM. Analysis of the expressions (7, 8) indicates that the concentration varies inversely proportional to the wind velocity u₁ and directly proportional to the vertical component of the turbulent exchange coefficient k₁/u₁. The impact of the horizontal component of the turbulent exchange coefficient is determined by k₀=k_y/u. Obtained expressions (7, 8) derived in result of an analytical approximation of a previously tabulated numerical solution of the equation of atmospheric diffusion with a logarithmic wind profile and a linear eddy diffusivity profile truncated by a constant value at the top of the surface layer.^16,17 This solution depends mainly on wind speed and direction, as well as on a stability parameter λ, which is a ratio of the eddy diffusivity at the given height z_l (for example, 1 m) to the product of z_l and wind speed at the same height (λ is related to the Richardson number or to the Monin-Obukhov stability parameter). Distribution of the surface concentration is characterized by its maximum q_m, which is obtained at a distance x_m from the source, as well as by functions describing its horizontal variations.

The distance x_m from emission point source, at which the concentration will obtain the maximum value, is calculated according to formulas (11, 12) correspondingly for volatile and non-volatile PM:³

$x_m=\frac{2}{3}\frac{u_1{H}^{1+n}}{k_1{\left(1+n\right)}^2}$     (11)

$x_m=\frac{u_1{H}^{1+n}}{k_1{\left(1+n\right)}^2\left(1.5+\omega \right)}$      (12)

Concentration of non-volatile PM (q_w, q_wm) is related with concentration of volatile PM (q, q_m) by following way at the distance x from emission source with height H:^16,17

$q_{\omega }=q\chi \left(\frac{w}{k_1},\frac{k_{1}x}{u_1},H\right)$     (13)

$q_{\omega m}=q_m{\chi }_m\left(\frac{w}{k_1},H\right)$    (14)

Differences in concentrations of volatile and non-volatile PM are caused mainly by the dimensionless parameter w/k₁. At same value of ω the sedimentation rate of PM will be different depending on the atmospheric turbulence intensity. In strong turbulence, for example, in the case of well-developed convection, the differences in the sedimentation velocity ω are manifested mainly for large x.

The mentioned features for nvPM distribution are included by functions (χ, χm), which are determined by formula (6) on the basis of numerical solution of the equation (2):

$\chi =\frac{{\left[\frac{u_1}{{\left(1+n\right)}^2{k}_1}\right]}^{\omega }{H}^{\omega \left(1+n\right)}}{\Gamma \left(1+\omega \right)\times x^{\omega }}$     (15)

The following dependences [15] for χ and χm were found for χ and χm on ω/k₁ and height H (Figure 2) (Table 1).

Analysis of analytical and numerical investigations¹² highlighted that the maximum concentration of nvPM is always higher and appropriate distance to the emission source is less than for volatile PM. Additionally, the dependence was obtained for χm on height H for ω/k₁ = const. As it is shown in Figure 2, the χm is practically independent of the height of emission source, which are displayed in surface layer. However, for higher emission sources, the value of χm increases relatively quickly with height H.

Figure 2 Dependence coefficients χ and χm on ω/k1 and height H.

Complex model PolEmiCa was used to calculate the maximum concentration of the exhaust gases (7) and PM fractions (8) in the plume from APU (height of installation was given H=4,5m), which is mounted on the aircraft Tupolev-154. Comparison of the distributions of PM fractions and gas for APU exhausts (), is shown correspondingly in Figure 3A, Figure 3B and between themselves (Figure 4). From Figure 3A there is evident higher concentration for PM close to the source of emission than for gas Figure 3B. Also, it may be concluded that PM polydispersity leads to the separation of maximums concentration in space for individual fractions on the wind direction and therefore it contributes to the reduction of maximum total concentration (Figure 4 in comparison with Figure 3A correspondingly). The coefficient χm for the maximum of surface concentration is substantially less dependent on the source height H than in the case of monodisperse PM, but it is still somewhat increases with H, especially when h>300m.¹⁶ The PolEmiCa model is under the improvement of the modeling PM dispersion in the atmosphere with taking in mind the investigated mechanisms and properties of PM, which are quite different in comparison with gaseous emissions.

Figure 3 Longitudinal distribution of PM10 (a) and gas (b) emitted by APU of Tupolev-154 along wind axis.

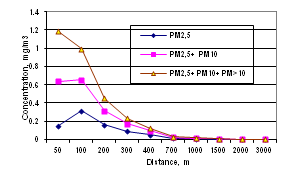
Figure 4 Longitudinal distribution of polydispersed PM2,5, PM10 and PM>10 emitted by APU of Tupolev-154 along wind axis.

Analysis of PM emission inventory results at major European and Ukrainian airports highlighted on sufficiently high contribution of aircraft engines and APU. PolEmiCa calculates the distributions of PM fractions for aircraft and APU exhausts (height of installation was given H=4.5m like for Tupolev-154). Calculation results of PolEmiCa for APU demonstrate that the maximum concentration of PM in exhaust from APU is higher and appropriate distance is less than in case for gas. Analysis of obtained result highlighted, that that PM polydispersity leads to the separation of maximums concentration in space for individual fractions on the wind direction and therefore it contributes to the reduction of maximum total concentration. The PolEmiCa model is under the improvement; including the modeling of PM dispersion in the atmosphere with taking in mind the investigated mechanisms and properties of the PM formation, which are quite different in comparison with gaseous emissions.

α                                  Coefficient, which takes into account the air pollutant transformation.
kx, ky, kz                     Coefficients of atmosphere turbulence, m2∙s-1
t                                   Time, s
U                                 Wind velocity, m∙s-1
q                                  Concentration of air contaminant, mg∙m-3
qm                                Maximum concentration of volatile PM, mg∙m-3
qωm                              Maximum concentration of non-volatile PM, mg∙m-3
w                                 Sedimentation rate of PM, g∙cm-1
ρ                                  Density of non-volatile PM, g∙cm-3
r                                   Radius of non-volatile PM, μm
H                                 Height of the emission source above ground level, m
М                                Emission rate, g∙s-1
n                                  Temperature stratification of the atmosphere

None.

None.

1. European Aviation Environmental Report. European Environment Agency: Denmark; 2006. 84p.
2. Herndon SC, Jayne JT, Lobo P. Commercial aircraft engine emissions characterization of in-use aircraft at Hartsfielde Jackson Atlanta International Airport. Environ Sci Technol. 2008;42(6):1877–1883.
3. Carslaw D, Beevers S, Ropkins K, et al. Detecting and quantifying aircraft and other on-airport contributions to ambient nitrogen oxides in the vicinity of a large international airport. Atmos Environ. 2006;40(28):5424–5434.
4. Peace H, Maughan J, Owen B, et al. Identifying the contribution of different airport related sources to local urban air quality. Environ Modell Softw. 2006;21(4):532–538.
5. Jung K, Artigas F, Shin J. Personal, indoor, and outdoor exposure to VOCs in the immediate vicinity of a local airport. Environ Monit Assess. 2011;173(1-4):555–567.
6. Eurocontrol. Long Term Forecast of Flights (2004-2025). Brussels: ESS; 2004. 40 p.
7. Stedman J, Linehan E, King K. Quantification of the Health Effects of Air Pollution in the UK for the Review of the National Air Quality Strategy. AEA Technology. 1999;4715(1):1‒26.
8. Morawska L, Ristovski Z, Jayaratne E. Ambient nano and ultrafine particles from motor vehicle emissions: characteristics, ambient processing and implications on human exposure. Atmos Environ. 2008;42(35):8113–8138.
9. Woody M, Haeng Baek B, Adelman Z, et al. An assessment of Aviation's contribution to current and future fine particulate matter in the United States. Atmospheric Environment. 2011;45(20):3424–3433.
10. Celikel A, Duchene N, Fleuti E, et al. Airport local air quality studies: Zurich Airport Emissions Inventory Using Three Methodologies. Eurocontrol: Brussels; 2004. 19p.
    Fraport Environmental Statement. Including the Environmental Program, until 2017. Fraport AG: Germany; 2015. p.24–30.
11. Berlyand ME, Onikul PI. Physical basis for air pollutants dispersion in atmosphere. Leningrad: GGO; 1968. pp. 3–27.
12. Zaporozhets O, Synylo K. PolEmiCA Local Air Quality Model Evaluation. AVIA-2015: The Proc. XII International scientific and technical conference. Кyiv, Ukraine; 2015. pp. 12–15.
13. Zaporozhets O, Synylo K. Modelling and measurement of aircraft engine emissions inside the airport area. Proceedings of XII International scientific and technical conference; 2015; Ukraine. pp. 65–71.
14. Berlyand ME, Gasilina NK, Genikhovich EL, et al. Method for Calculation of Concentrations of Air Pollutants the Industrial Emission Contains. National
15. Regulatory Document OND-86. Hydro meteorological Publishers: Newyork; 1987. 92 p.
16. Berlyand ME. Prediction and Regulation of Air Pollution. Gimiz: Leningrad; 1985. 272 p.  
17. Berlyand ME. Problems of industrial air pollution modelling considering soviet experience. Air Pollution Modeling and Its Application VIII, Edited by Han van Dop and Douw G Steyn. Proceedings of the Eighteenth NATO/CCMS International Technical Meeting on Air Pollution Modeling and Its Application; 1990 May 13-17; Vancouver, British Columbia, Canada. New York: Springer Science+Business Media; 1991. p. 1‒13.