In this paper deformation and breakup of a non-Newtonian shear thinning droplet are studied parametrically. The effects of physical and geometrical properties are investigated by means of numerical methods. The flow is simulated in the range of 716 up to 2864 for Reynolds number and 8.5 to 70 for the Weber number. The VOF numerical method is used for capturing the droplet deformation and Carreau model is used to simulate non-Newtonian physical properties. The results are compared with those exist in literature. It is found that various non-Newtonian parameters of the fluid properties do affect the critical Weber number and the deformation of the droplet.

Keywords: deformation, breakup, non-Newtonian droplet, numerical simulation

u Velocity vector

u Velocity in x direction

v Velocity in y direction

p Pressure of environment

υ  Dynamic viscosity of environment

σ Surface tension coefficient

F_st Surface tension force

γ ˙ Strain rate

t Time

x Position

ρ₂ Density of gas

μ₁ Viscosity of droplet

μ₂ Viscosity of fluid

k Surface curvature

n Surface normal vector

r Radius of droplet

d Diameter of droplet

ρ₁ Density of droplet

ρ Density of fluid

n Power index

μ₀ Viscosity at zero strain rate

μ_∞ Viscosity at infinite strain rate

λ Relaxation time

We Weber number

Oh Ohnesorge number

Re Reynolds number

Time/T^* Non-dimension time

φ  liquid volume of fraction

A large number of flows in nature and industries involve free surfaces or material interfaces and their applications are in environmental sciences, geophysics, physics and different engineering problems. Droplets also paly vital roles in nature and different areas of sciences and engineering which deformation is the main effective factor in their qualities, such as fuel sprays, cleaners and painting. Considering the importance of the subject, a great deal of research has been conducted on deformation of Newtonian and non-Newtonian droplets experimentally and numerically. Krzeczkowski¹ studied the breakup and deformation of the Newtonian droplet in gas flow and examined various deformation and breakup mechanisms experimentally. He illustrated that breakup time strongly depends on the Weber number, We, and density ratio. Berthoumieu et al.,² studied second breakup of Newtonian droplets injected in mixed layer of two high speed air flows and with same directions experimentally. Also the deformation of two-dimensional water Newtonian droplet inside a channel was investigated by Shirani & Masoomi.³ Local properties of secondary breakup of the Newtonian droplets in multimode regime were studied by Dai and Faeth.⁴ In this experimental investigation, the density ratio is larger than 500, Ohnesorge number, Oh, is less than 0.1, and range of We is from 15 to 150. The critical Weber number for each breakup regime was reported. In the study, the effect of surface tension was investigated by using surface stress method, volume of fluid, VOF, algorithm, and Collocated grid. Ghadiri et al.,⁵ studied numerical simulation of Newtonian droplet breakup and deformation in Newtonian uniform fluid at different surface tension coefficient and the studied parameters were droplet elongation, droplet velocity, location of the center of gravity, and drag coefficient of the droplet. Horwitz et al.,⁶ investigated deformation of a spherical Newtonian droplet in a square channel flow for moderate Reynolds numbers. The deformation and secondary breakup of the droplets were studied experimentally by Hsiang and Faeth⁷ and the effects of the Weber, Ohnesorge and Reynolds numbers were investigated. Primary deformation and breakup of a spherical droplet in shear and bag modes were numerically studied by VOF algorithm and finite difference method by Kekesi et al.⁸ They found that the critical Weber number was 12.

In various industries such as printing, paint and coating, electronics or industries where heat transfer is important, adding nano particles changes the nature of the fluid to be non-Newtonian fluid. Hu et al.,⁹ studied breakup and coalescence of droplets of fluids which contain surface tension reducers. They studied effects of co-polymers on Polybutadiene droplets in Polydimethylsiloxane using a four-roll mill flow cell and found out a reaction in functionalized Homopolymers decline interfacial tension and thus increases breakup. Hang et al.,¹⁰ examined the numerical transfer of ink drops between two parallel plates and a plate and a guard and studied the effect of factors such as contact angles of ink drop with the two surfaces as well as physical properties of the drop in Newtonian conditions on breakup time and droplet size after breakup. In experimental studies done by Tamjid,¹¹ it was shown that if the concentration of the nanoparticles was about 10%.wt, there would be a good coincidence between estimated results and Carreau relation, experimentally. Pudas¹² investigated the ink droplets transfer in micro scale in offset printing method. In this study, the method for the usage of conductive ink in electronics industry was investigated. The applications of this technology are in flexible LCDs, batteries, nutritious industry, health, solar cells, and production of flexible electronic pads with low cost.

In 2011, using the Carreauo non-Newtonian model and the VOF method for non-Newtonian fluid containing solid particles, simulation of fluid transfer rates with contact angles of the bottom and top plates, Capillary number as well as different top plate velocity were carried out by Ahmad et al.¹³ In 2011, Ghadiri et al.,¹⁴ studied numerically the deformation and breakup of the non-Newtonian micro drop containing silver nanoparticles trapped in a cavity and a detachable flat plate.

In liquid fuel engines the efficiency and stability of the combustion highly depend on breakup of the droplets. In this application, the increase in the breakup rate of droplets and their size reduction lead to the improvement of combustion process and reduction of complete combustion time. This phenomenon causes the reduction of the combustion chamber size and thus shorter engine cycles. Other advantages of the improvement of the droplets breakup are uniform temperature in the combustion chamber and reduction in environmental pollutants. Park et al.,¹⁵ experimentally investigated the microscopic and macroscopic characteristics of breakup and atomization of diesel droplets from injection in intersecting air flow.

Many of the industrial fluids have non-Newtonian nature. Mighri et al.,¹⁶ conducted an empirical study of a drop of fluid in the surrounding environment, both of which had viscoelastic properties. Favelukis et al.,¹⁷ studied the deformation and breakup of a non-Newtonian droplet in a simple tensional flow and creeping flow theoretically. The power law was selected for the internal flow of the droplet. The mode of the droplets breakup can be very different and it depends on the properties and composition of the droplets. Dongming et al.,¹⁸ investigated the breakup of a droplet in an axisymmetric tensional flow with various Capillary numbers using VOF method. The critical Weber number indicates the threshold of the increase in hydrodynamic instability and corresponds to the onset of droplet breakup. According to the Taylor analogy breakup model, the dependence of the critical Weber number on density ratio for droplets with different size was studied analytically by Omidvar et al.¹⁹ Tarnogrodzki²⁰ had theoretically predicted the critical Weber number and studied a droplet in the gas flow for the bag breakup model.

In present study, we carried out a numerical investigation of deformation and breakup of a non-Newtonian shear thinning fluid droplet and implemented the VOF method to capture the droplet deformation when the Newtonian fluid flows over the droplet. The Carreau model was chosen to handle the shear thinning effect for the non-Newtonian droplet. On the basis of the simulation results, a detailed explanation for the deformation and breakup stages of the droplet was developed when the droplet deformation occurred. In addition, the influence of the non-Newtonian parameters, dimensionless numbers of large Reynolds and different Weber numbers on the deformation and breakup of non-Newtonian spherical droplet were explored.

To study non-Newtonian deformation and breakup drop, axisymmetric geometry was selected and the boundary conditions and the numerical domain are shown in Figure 1. In the present study, we consider a laminar Newtonian gas (air) flow across the non-Newtonian droplet fluid and then deformation occurs. The boundary conditions and studied geometry are shown in Figure 1. The droplet shape is axisymmetric before breakup and thus the numerical domain is considered asymmetrically. For unsteady incompressible flow of immiscible non-Newtonian droplet in air, the continuity and momentum equations are

$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho u)=0$   (1)

$\frac{\partial (\rho u)}{\partial t}+\nabla .(\rho uu)=-\nabla p+\nabla .(\mu \nabla u)+F_{g+}{F}_{st}$   (2)

Figure 1 Flow configurations and boundary conditions.

where, ρ is the density, $u=(u,v)$ is the velocity vector, p is the pressure, µ₀ is the viscosity, and F_st is the surface tension force. To capture the interface between the droplet and the surrounding air, an additional transport equation for the liquid volume fraction is solved. The liquid volume of fraction is denoted by φ and is defined by,

$\phi =\{\begin{array}{cc}1& insidethedroplet\\ 0& outsidethedroplet\\ 0<\phi <1& at\mathrm{interface}cells\end{array}$   (3)

and the transport equation for φ is,

$\frac{\partial \varphi }{\partial t}+u\cdot \nabla \varphi =0$   (4)

However, the density ρ and dynamic viscosity μ for the free surface of the computational domain are calculated from the volume fraction φ using the following expressions,

$\rho =\varphi {\rho }_1+(1-\varphi ){\rho }_2$   (5)

$\mu =\varphi {\mu }_1+(1-\varphi ){\mu }_2$   (6)

The subscripts _‘1’ and _‘2’ refer to the liquid (droplet) and gas (environment) phases, respectively. Here, the surface tension force is determined with the Brackbill equation,²¹

$F_{st}=\sigma kn$   (7)

where σ is the surface tension coefficient, k is the local free surface curvature and n refers to the unit normal vector of the free surface. The local free surface curvature k and normal vector of the free surface n are calculated from,

$n=\nabla \varphi /\left|\nabla \varphi \right|$   (8)

$k=-\nabla .n$   (9)

The Carreau²² model is used for viscosity of a non-Newtonian shear thinning fluid,

$\frac{\mu -{\mu }_{\infty }}{{\mu }_0-{\mu }_{\infty }}={\left[1+{(\lambda \stackrel{·}{\gamma })}^2\right]}^{\frac{(n-1)}{2}}$   (10)

where μ₀ is the droplet viscosity at zero strain rate (at very low strain rate according to non-Newtonian Carreau model Eq.10 the viscosity approaches to μ₀), μ_∞ is the droplet viscosity at infinite strain rate, λ is the time constant, n is the power law index (where n<1 corresponds to the shear thinning effect) and $\stackrel{·}{\gamma }$ is the shear rate, which is defined as:

$\dot{\gamma }=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}$   (11)

Momentum and continuity equations (Eq. 1 and Eq. 2), were discretized using the finite volume approach and pressure–velocity coupling was addressed by using the SIMPLEC algorithm. A second-order upwind scheme was used to evaluate the fluxes at the cell interfaces. The gravitational force and the surface tension force are included in the source term. The explicit Euler scheme for time advancement in the transport equation of φ was employed. The resulting system of algebraic equations was then solved respectively at each time step. The non-dimensional parameters are:

The Weber number:

$We=\frac{\rho v^{2}d}{\sigma }$   (12)

The Ohnesorge number:

$Oh=\frac{{\mu }_1}{\sqrt{{\rho }_1\sigma d}}$   (13)

The non-dimensional time:

$T^{\ast }=\frac{d}{v}\sqrt{\frac{{\rho }_2}{{\rho }_1}}$   (14)

The Reynolds number:

$Re=\frac{\rho vd}{\mu }$   (15)

For validation of the results, the deformation of the Newtonian droplet (by substituting n=1) was simulated as shown in Figure 2. The results are in good agreement in comparison with the results obtained by Ghadiri et al (2012). Figure 2 shows deformation parameter (L/t) with non-dimensional time.

Figure 2 Deformation of droplet as a function of time.

In this study, the breakup and deformation of the droplets in the range of high Reynolds numbers at 716, 1432, and 2864 and also at We=8.5, 15, 35, and 70 for both of Newtonian and non-Newtonian fluid were studied. Re=1432 and We=35 were considered as the base values and in each state one of the numbers was fixed and others varied. For each state, various amounts of different parameters were considered. Carreau model parameters (n-power index, λ-relaxation time, µ₀-viscosity at zero strain rate and µ_∞-viscosity at infinity strain rate) were examined. The rheological properties of non-Newtonian fluid for different Reynolds and Weber numbers were studied. The grid dependency is studied and as shown in Figure 3, for grid sizes smaller than 256×512, results were independent of grid number. Droplet and ambient fluids properties are listed in Table 1.

Figure 3 Velocity over the symmetric axis for various computational cells.

Droplet deformation of non-Newtonian fluid

Deformation of droplet of non-Newtonian fluid for different rheological parameters for Re between 716 to 2864 is investigated and effects of all of the non-Newtonian parameters n, λ, µ₀ and µ_∞ are investigated too. Due to flow of Newtonian uniform fluid around the droplet, the droplet deformation occurs. Figure 4 shows deformation of droplet from the earlier times until the breakup time. The time history of the droplet deformation for different non-Newtonian index and µ₀ at Re=1432 are shown in Figure 4 for non-dimensional time 1.875. Analyzing the effect of n and µ₀ demonstrates that deformation of droplet increases when n and µ₀ reduce.

Figure 4 Droplet deformation for different non-Newtonian at Re=1432.

Power index

Figures 5,6 and 7 show conditions at various values of L/t during the breakup process. The effect of power index, n, of non-Newtonian fluid on deformation of the droplet is investigated. Figure 5 shows the deformation parameter as a function of time for different values of n at Re=1432, We=35. As shown, the process of deformation can be divided into three parts:

• Smooth changes area (area 1 in Figure 5)
• Moderate changes area (area 2 in Figure 5)
• Sharp changes area (area 3 in Figure 5)

In area 1, strain rate is small and surface tension force of droplet is high and then the droplet deformation is very slow. In area 2, when strain rate increased viscosity decreases and because the fluid loses its strength to maintain its shape, deformation rate increases. In area 3, strain rate is very large and surface tension force of droplet is low and then the droplet deformation is very sharp. According to Figure 5, the deformation parameter, L/t, increases when the fluid has more shear thinning behavior, i.e. n becomes small. For Re=1432, when n decreases from 0.6 to 0.4, deformation parameter shows an increase of 23% and when n decreases from 0.733 to 0.6, deformation increases 81%. When n value decreases from 0.733 to 0.6, breakup time decreases 9% and when n decreases to 0.4, breakup time decreases 13%.

Figure 5 Deformation parameters coefficient for different values of n at Re=1432 and We=35.

Deformation parameters, L/t, as a function of time for different Re at basic value of n are shown in Figure 6. As it can be seen in the Figure 6, at n=0.733, when Re increases from 716 to 1432, deformation parameter increases by 15% and when Re increases from 1432 to 2864, deformation parameter increases 13%. Therefore, the slope of the diagram increases as Re goes up. But Re changes do not have any effects on breakup time. Thus, it can be concluded that the breakup time does not depend on Reynolds number for the ranges studied in this paper.

Figure 6 Deformation parameters as a function of time for different Re at n=0.733 and We=35.

Effect of zero strain rate

Figure 7 shows the deformation parameter, L/t, as function of non-dimensional time for different values of μ₀ at Re=1432. When μ₀ reduces from 0.227 to 0.1135, L/t increases by 72% and L/t decreases by 198% by doubling μ₀ from basic value. When amount of μ₀ is halved, the breakup time decrease by 7% and if the value of μ₀ increase from 0.227 to 0.454, the breakup time experiences a 22% decline.

Figure 7 Deformation parameters for different μ₀ at Re=1432 and We=35.

Comparison between Newtonian and non-Newtonian fluid droplet at different Re

The effect of Newtonian and non-Newtonian droplets on droplet deformation has been compared for Re=716, 1432, 2864, We=35, and Oh=1.75 (Ohnesorge number) that Figure 8 shows the shape of droplet in same non-dimensional time for Newtonian droplet. For Newtonian droplet due to constant viscosity, the deformation is rather constant and the process is slow and the Re is the only factor of more deformation of the droplet. Note that as the deformation takes place, the shape of droplet changes and the drag force and deformation change as well. In a similar non-Newtonian state as shown in Figure 9, breakup happens for all Re at non-dimensional time, Time/T^*=1.2 and its value of the L/t reaches 150, while in Newtonian case at Time/T^*=4, deformation parameter has not reached to 6 and breakup has not occurred yet.

Figure 8 Droplet deformation for different Re at base conditions.

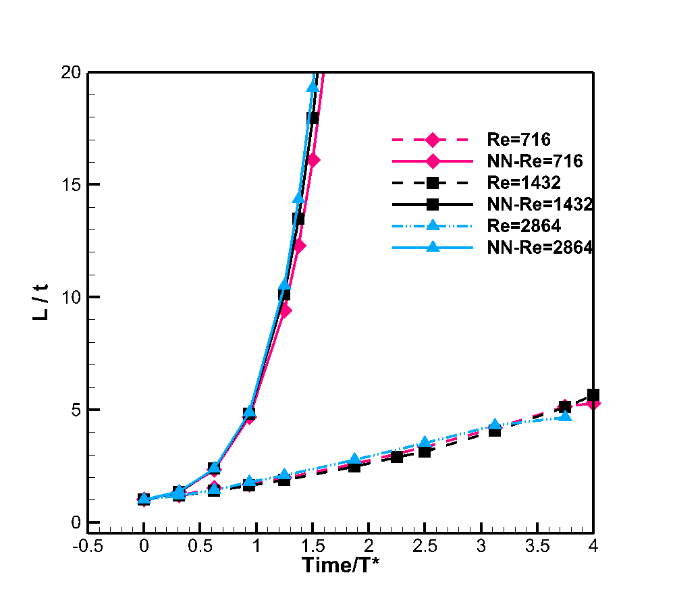
Figure 9 Deformation parameter for Newtonian and non-Newtonian fluids (NN) and different Re at Oh=1.75.

Surface tension forces for non-Newtonian fluids

In this section in order to study the effects of surface tension forces on deformation of non-Newtonian droplet for different rheological parameters n, µ_0, µ_∞ and λ, values of We from 8.5 to 70 have been investigated at dimensionless time 1.875 and the results have been compared with Newtonian droplet in similar conditions. Flowing stream on droplet changes pressure and speed in both sides of droplet which lead to deformation and droplet changes to disk shape. Droplet will break from thinner part if flow We is more than critical We. Location of broken area will be similar to Figure 10 if there is an increase in We. It should also be mentioned that tension force helps breakup by clincher action in this step.

Figure 10 Droplet deformation for different We at n=0.733.

Power index

Figures 11, 12, 13 and 14 show conditions at various values of the deformation parameter, L/t, during the breakup process at different We. The effect of power index, n, of non-Newtonian fluid on deformation of the droplet is investigated. Figure 10 shows the deformation parameter as a function of Time/T^* for different values of n at We=8.5. The maximum amount of L/t occurs at Time/T^*=1.25 for all values of n, and then a downward trend is seen until 3.125 the minimum value of L/t happens. The reduction of the surface tension leads to an increase in We and a decrease in fluid resistance against deformation. Droplet tends to keep primary shape because the ratio of surface tension to inertia force is high but owing to reduction of inertia force the ratio changes during deformation, furthermore we can see oscillating mode in amount of L/t as shown in Figure 11.

Figure 11 Deformation parameter for different n at We=8.5.

L/t for different n at We=15 are shown in Figure 12 and it shows that L/t rise is observed by 106% when (shear thinning property of fluid is more than its primary state) amount of power index from n=0.733 to n=0.6 is decreased. While the value of n is decreased from 0.733 to 0.4, the amount of L/t experiences a 193% increase. Figure 13, shows L/t for n=0.4, 0.6 and 0.733 at We=70 on Time/T^*=1.75 and as a result L/t increases by 56% and 80% while the value of n is reduced to 18% and 45% of the base value at We=70, respectively. The changes of parameter n affect the breakup time. For example, when the value of n reduces from 0.733 to 0.6 or from 0.733 to 0.4, the breakup time reduces and breakup occurs. Results of We=35 are also shown in Figure 5.

Figure 12 Deformation parameter for different n at We=15.

Figure 13 Droplet deformation parameter for different n at We=70.

By studying the effect of the Weber number on the value of L/t, the following results are obtained:

1. Due to the reasons that are mentioned below, there is an oscillation in deformation at We=8.5:

1. At Time/T^*=0, the ratio of inertia value to surface tension is high, thus an increment in value of deformation is seen.
2. Movement and increase in speed of droplet lead to decrease in its relative speed which increases ratio of surface tension force and inertia force. Thus it prevents droplet deformation and droplet returns to primary shape since surface tension force inhibits deformation.
3. Owing to crossed stream around droplet, wake is different in initial time because the droplet is static and ratio of inertia to surface tension force (because of the increase in droplet speed at next times) is various.

2. Due to change in the shear thinning property of the fluid and the higher surface tension at We=15 rather than We=35 or 70, the amount of changes of L/t at We=15 is more than L/t changes at We=35 or 70 and it shows that the droplet is located at the critical We
3. Comparison between the rate of L/t for different We shows that, at We=15, area with smooth changes (area 1) continue until about Time/T^*=2.5 and in result, moderate area (area 2) will become smaller than We=35 or 70.

Overall, when We increases from 8.5 to 15 at n=0.733, the amount of L/t increases 3.44 times and We change from 15 to 35 corresponds to an increase of 358%. When We increases from 35 to 70, L/t increases 1.85 times and when We increases from 8.5 to 70, L/t increases 21.5 times, which is shown in Figure 14.

Figure 14 Deformation parameter for different We at n=0.723.

Effect of zero strain rates

In this part, the effect of zero strain rate at various We has been studied. Figure 15 demonstrates the deformation parameter, L/t, as function of non-dimensional time, Time/T^*, for different values of µ₀ (at Time/T^*=1.875). While L/t increases by 50% at We=15, µ₀ changes from base value to 0.454 and also L/t will decrease by 90% if µ₀ declines from 0.227 to 0.1135. It should also be mentioned that the breakup time increases by 33% when µ₀ is decreased by half and if it is increased by factor of two, the breakup of the droplet does not happen.

Figure 15 Deformation parameter for different μ₀ at We=15.

According to Figure 16 to show L/t for different value of µ₀ at We=70 (at time dimensionless 1.75), when the value of µ₀ reduces from 0.227 to 0.1135, the value L/t parameter increases by 71% and by 100% increase in the value of viscosity relative to the base value, the deformation decreases by 66%. In addition, at We=35, when μ₀ decreases 50% from the base value, the breakup time decreases 7%. However, when it decreases 100%, the breakup time increases by 22%.

Figure 16 Deformation parameter for different μ₀ at We=70.

All non-Newtonian parameters of the Carreau model have been examined at Re from 716 to 2864 and We from 8.5 to 70. Because the trends of deformation droplet are similar but they have different value of L/t, some results are presented. For example, the effect of μ_∞ is a little more than μ₀. Based on gain results of the examination of relaxation time effect, λ, it can be concluded that effect of λ on the deformation and breakup time is insignificant. However, Figure 17 shows the effect of this parameter, λ, on L/t quite clearly at We=15. It shows that the droplet is at critical We range because a little change of λ causes increase in the viscosity changes and deformation.

Figure 17 Deformation parameter for different λ at We=15.

Comparison between Newtonian and Non-Newtonian fluid droplet at different We

Differences of the effect of Newtonian and non-Newtonian droplets on deformation parameter, L/t with respect to Time/T^* and Weber numbers are illustrated by Figure 18. Comparing these graphs explains that changes rate of L/t is very low for Newtonian state, but due to the nature of non-Newtonian shear thinning droplet, changes rate of L/t is very high. For example, (at dimensionless time=1.875), if the physical properties of droplet changes from Newtonian to non-Newtonian at We=8.5, 15, 35, 70, then amount of deformation will be 0.45, 3.86, 18.35, 27.92, respectively. Also, owing to the effect of ratio inertia force changes to surface tension force, the oscillation mode of L/t is seen at We=8.5 for both states. But in Newtonian state at We=8.5, the rate of oscillation value of L/t is less than non-Newtonian state.

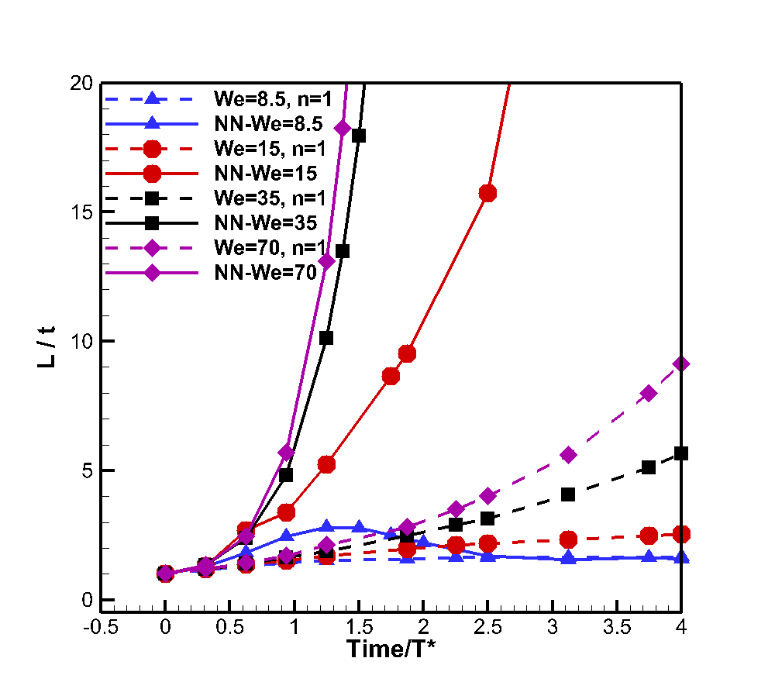
Figure 18 Deformation parameter for Newtonian and non-Newtonian fluids (NN) and different We at Re=1432.

Breakup time

Knowing the time limit of the breakup in flows with different Reynolds and Weber numbers is very important to system design, efficiency improvement optimization. In this paper, it is assumed that the nature of the deformation does not change and its mode is fixed.

Effect of Re of the flow

Breakup time of droplet at different Re has been shown in Figure 19. It illustrates that the breakup time will increase when Re increases to 50 because the deformation mode is different. But for Reynolds numbers from 50 to 100, the breakup time reduces and it continues until 1000 and after that increase in Re will have no effect on the breakup time because the shear stress of flow becomes low.

Figure 19 Breakup time of droplet at different Re.

The effect of Weber number 

At weber numbers below 15, the surface tension forces overcome the inertial forces and breakup does not happen in this range. At higher weber numbers, inertial forces increase and collapse the surface tension forces and so breakup occurs. By increasing We, the non-dimensional breakup time reduces until We=140 and after that because of the different breakup modes, We doesn't have an important effect on breakup time. Results are presented in Figure 20. investigating and comparing the breakup time for a Newtonian and non-Newtonian (present study) droplets at various We, it can be concluded that effective range of Weber numbers at breakup time for Newtonian and non-Newtonian fluids are similar at We=15 to 140 that results are presented in Figure 21.

Figure 20 Breakup time of droplet at different We.

Figure 21 Comparison of break time of Newtonian and non-Newtonian droplet at different We.

In this study, numerical simulation of deformation and breakup for Newtonian shear thinning fluid under laminar Newtonian surrounding fluid at high Reynolds number and based on surface tension force has been performed. VOF method and Carreau non-Newtonian model have been used for simulation. Results illustrated that increment of deformation parameter, L/t and then the rate of deformation by decrement of parameters of n, μ₀, μ_∞, Weber, Ohnesorge and Reynolds numbers. But the variation of Lambda does not effect on value of L/t except at We=15 that droplet locate in critical weber number. Also the Reynolds number has no effects on breakup time at different values of n, μ₀, μ_∞. In addition, at We=8.5, breakup does not occur. However, fluctuations are observed in the amount of deformation, which has a maximum and a minimum value. Therefore, breakup is not observed at Weber numbers under the critical We. The value of deformation changes by changing of non-Newtonian properties, but different variations are seen at We=15 because it is in range of critical Weber numbers. In study of various non-Newtonian parameters for Reynolds number from 716 to 2864 and their comparison with deformation, it was observed that the droplet converts from circle to disk at large Reynolds. Due to constant viscosity of Newtonian droplet, the rate of deformation is slow while it is sharp for non-Newtonian droplet it will be more if parameters of n, μ₀, μ_∞ increase. The effective limit of Weber number for Newtonian and non-Newtonian breakup is from 15 to140 because there is no breakup for less than 15 and at more than 140, We has very low effect.

None.

Authors declare that there is no conflict of interest.

1. Stefan A Krzeczkowski. Measurement of liquid droplet disintegration mechanisms. Int J Multiphase Flow. 1980;6(3):227–239.
2. Berthoumieu P, Carentz H, Villedieu P, et al. Contribution to droplet breakup analysis. International Journal of Heat and Fluid Flow. 1999;20(5):492–498.
3. Shirani E, Masoomi S. Deformation of a droplet in a channel flow. Journal of Fuel Cell Science and Technology. 2008;5(4):041008.
4. Dai Z, GM Faeth. Temporal properties of secondary drop breakup in the multimode breakup regime. International Journal of Multiphase Flow. 2001;27(2):217–236.
5. Fatemeh Ghadiri Modarres. Numerical Simulation of the Droplet Breakup with Emphasize on the Effect of Surface Tension. Department of Mechanical Engineering: Isfahan University of Technology, Iran; 2012.
6. Horwitz JAK, Kumar P, Vanka SP. Three-dimensional deformation of a spherical droplet in a square duct flow at moderate Reynolds numbers. International Journal of Multiphase Flow. 2014;67:10–24.
7. Hsiang LP, Faeth GM. Near-limit drop deformation and secondary breakup. International Journal of Multiphase Flow. 1992;18(5):635–652.
8. Kékesi T, Amberg G, Prahl Wittberg L. Drop deformation and breakup. International Journal of Multiphase Flow. 2014;66:1–10.
9. Hu YT, Pine DJ, Gary Leal L. Drop deformation, breakup, and coalescence with compatibilizer. Physics of Fluids. 2000;12(3).
10. Huang WX, Lee SH, Sung HJ, et al. Simulation of liquid transfer between separating walls for modeling micro-gravure-offset printing. International Journal of Heat and Fluid Flow. 2008;29(5):1436–1446.
11. Tamjid E, Bernd H Guenther. Rheology and colloidal structure of silver nanoparticles dispersed in di-ethylene glycol. Powder Technology. 2010;197(1-2):49–53.
12. Pudas M, Hagberg J, Leppavuori S. Printing parameters and ink components affecting ultra-fine-line gravure-offset printing for electronics applications. Journal of the European Ceramic Society. 2004;24(10-11):2943–2950.
13. Ahmed DH, Sung HJ, Kim DS. Simulation of non-newtonian ink transfer between two separating plates for gravure-offset printing. International Journal of Heat and Fluid Flow. 2011;32(1):298–307.
14. Ghadiri F, Ahmed DH, Sung HJ, et al. Non-Newtonian ink transfer in gravure-offset printing. International Journal of Heat and Fluid Flow. 2011;32(1):308–317.
15. Sung Wook Park, Sayop Kim, Chang Sik Lee. Breakup and atomization characteristics of mono-dispersed diesel droplets in a cross-flow air stream. International Journal of Multiphase Flow. 2006;32(7):807–822.
16. Mighri F, Ajji A, Carreau PJ. Influence of elastic properties on drop deformation in elongation flow. J Rheol. 1997;41(5):1183–1201.
17. Favelukis M, Lavrenteva OM, Nir A. Deformation and breakup of a non-Newtonian slender drop in an extensional flow. J Non-Newtonian Fluid Mech. 2005;125(1):49–59.
18. Dongming Yu, Manman Zheng, Taoming Jin, et al. Asymmetric breakup of a droplet in an axisymmetric extensional flow. Chinese Journal of Chemical Engineering. 2016;24(1):63–70.
19. Amir Omidvar, Hassan Khaleghi. An Analytical Approach for Calculation of Critical Weber Number of Droplet Breakup in Turbulent Gaseous Flows. Arabian Journal for Science and Engineering. 2012;37:2311–2321.
20. Tarnogrodzki A. Theoretical prediction of the critical weber number. International Journal of Mutiphase Flow. 1993;19(2):329-336.
21. Brackbill JU, Kothe DB, Zemach C. A continuum method for modeling surface tension. J Comput Phys. 1992;100(2):335–354.
22. Carreau PJ. Rheological Equations from Molecular Network Theories. Trans Soc Rheol. 1972;16(1):99–127.