Lighthill considered the diffraction of normal shock wave past a small bend of angle d. Srivastava and Srivastava and Chopra extended the work of Lighthill to the diffraction of oblique shock wave (consisting of incident and reflected shock wave). Chopra and Srivastava further carried forward their work when the diffraction of oblique shock wave takes place with yawed wedges. In the present investigation curvature of the reflected diffracted is obtained when the interaction takes place with yawed wedge and the relative outflow behind reflected shock wave before diffraction is subsonic.

Keywords: curvature, diffraction reflection, yawed wedge, subsonic.

Lighthill¹ considered the diffraction of a normal shock wave past a small bend of small angle d. The analogous problem of a plane shock wave hitting the wall obliquely together with the reflected shock has been solved by Srivastava² and Srivastava & Chopra.³ Srivastava² solved the problem when the relative outflow behind reflected shock before diffraction is sonic and subsonic. Srivastava & Chopra³ solved the problem when the relative outflow behind the reflected shock wave before diffraction is supersonic. Srivastava⁴ gave the results concerning curvature of the reflected diffracted shock when the relative outflow behind the reflected shock before diffraction is sonic; subsequently he solved the curvature of reflected diffracted shock⁵ when the relative outflow before diffraction is subsonic. Chester⁶ considered the problem of reflection and diffraction of normal shock wave interacted by yawed wedges which was the extension of Lighthill’s¹ problem of diffraction of a normal shock wave past a small bend. The results of Srivastava² and Srivastava & Chopra³ have been extended results to the case of yawed wedges Chopra & Srivastava.⁷ More specifically the attempt is concerned with the interaction of an oblique shock configuration (consisting of incident and reflected shock) with an yawed wedge i.e. the shock line (line of intersection of incident and reflected shock) makes some non zero angle with the leading edge of the wedge. In the present case curvature results have been obtained for the yawed case when the relative outflow behind reflected shock before diffraction is subsonic.

Let the velocity pressure, density and sound speed ahead of the shock wave be denoted by $o, p_0, {\rho }_{0, }{a}_0$ in the intermediate region by $q_1, p_1, {\rho }_1,a_1$ and behind the reflected shock by $q_2, p_2, {\rho }_2,a_2$ . Let U denote the velocity of intersection of the incident and reflected shock, δ the angle of the bend, ${\alpha }_0$ is the angle of incidence and ${\alpha }_2$ is the angle of reflection. The Rankine-Hugoniot equation across incident and reflected shock for$\gamma =1.4$  (g being the ratio of specific heats are gives as follows Srivastava.^8,9 Across the incident shock (Figure 1).

$q_1=\frac{5}{6}U\sin {\alpha }_0\left(1-\frac{a_0^2}{U^2{\sin }^2{\alpha }_0}\right)$   (1)

$p_1=\frac{5}{6}{\rho }_0\left(U^2{\sin }^2{\alpha }_0-\frac{a_0^2}{7}\right)$     (2)

$\rho =\frac{6{\rho }_0}{\left(1+\frac{5a_0^2}{U^2{\sin }^2{\alpha }_0}\right)}$ 

$a_0=\sqrt{\frac{\gamma p_0}{{\rho }_0}}$   (3)

Across the reflected shock

${\overline{q}}_2={\overline{q}}_1+\frac{5}{6}\left(U^{*}-{\overline{q}}_1\right)\left(1-\frac{a_1^2}{{\left(U^{*}-{\overline{q}}_1\right)}^2}\right)$     (4)

$p_2=\frac{5}{6}{\rho }_1\left\{{\left(U^{*}-{\overline{q}}_1\right)}^2-\frac{a_1^2}{7}\right\}$    (5)

${\rho }_2=\frac{6{\rho }_1}{1+\frac{5a_1^2}{{\left(U^{*}-{\overline{q}}_1\right)}^2}}$       (6)

Where ${\overline{q}}_2=q_2\sin {\alpha }_2,$${\overline{q}}_1=-q_1\cos \left({\alpha }_0+{\alpha }_2\right)$

$U^{*}=U\sin {\alpha }_2,$ $a_1=\sqrt{\frac{\gamma p_1}{{\rho }_1}}$ 

Also we have

$q_1\cos {\theta }^{\prime }=q_2\cos {\alpha }_2,$${\theta }^{\prime }={\alpha }_0+{\alpha }_2-\frac{\pi }{2}$

As the oblique shock configuration advances over a yawed wedge (shock line making some non zero angle with the leading edge of the wedge) the velocity of the point of intersection of the leading edge and shock line moves with velocity $U\text{cosec}\chi$ , U being the velocity of shock line and $\chi$ being the angle of yaw (Figure 2).

By superimposing a velocity on the whole field in a direction opposite to the direction of motion of the point of intersection of the shock line and the leading edge, the shock configuration becomes stationary and the resulting velocity behind the reflected shock for stationary configuration say V2 is given by

$V_2^2=U^2{\text{cosec}}^2\chi +q_2^2-2U{q}_2$    (7)

For conical field flow to occur behind the reflected shock $\raisebox{1ex}{$V_2$}\!\left/ \!\raisebox{-1ex}{$a_2$}\right.$ should be greater than 1 which from (7) gives the condition that we should have

${\text{sin}}^2\chi <\frac{U^2}{a_2^2+2U{q}_2-q_2^2}$    (8)

We have also the relation

$\tan \mu =\frac{U-q_2}{U\text{cosec}\chi }$     (9)

Further the semi angle of the Mach cone is given by

$\sin \alpha =\frac{a_2}{V_2}$       (10)

Let the disturbed flow variable behind the reflected diffracted shock referred to $Ox\text{'}y\text{'}z\text{'}$ axes be denoted by

${\overrightarrow{V}}_2=\left(u_2, v_2,V_2+w_2\right), p_2^{\text{'}}, {\rho }_2^{\text{'}}, S_2^{\text{'}}$      (11)

where $u_2, v_2,w_2$ are small perturbation in the velocity along $0x^{\prime }, 0y\text{'}$ $0z\text{'}$ and respectively,$$p_2^{\text{'}}$$ is the pressure,$p_2^{\text{'}}$ ${\rho }_2^{\text{'}}$ is the density and$S_2^{\text{'}}$ is the entropy. Using conservation laws we obtain the flow equations as

${\overrightarrow{V\text{'}}}_2\nabla p_2^{\text{'}}+{\rho }_2^{\text{'}}\nabla {\overrightarrow{V\text{'}}}_2=0$     (12)

$\left({\overrightarrow{V\text{'}}}_2\nabla \right){\overrightarrow{V\text{'}}}_2+\frac{1}{{\rho }_2^{\text{'}}}\nabla {\rho }_2^{\text{'}}=0$    (13)

${\overrightarrow{V\text{'}}}_2\nabla S_2^{\text{'}}=0$     (14)

We introduce the following transformations

$x=\frac{x\text{'}}{z\text{'}\tan \alpha }$M

$x=\frac{x\text{'}}{z\text{'}\tan \alpha }$   

$p=\frac{p_2^{\text{'}}-p_2}{a_2{\rho }_2{q}_2}$        (15)

$\rho =\frac{a_2\left({\rho }_2^{\text{'}}-{\rho }_2\right)}{{\rho }_2{q}_2}$

$u=\frac{u_2}{q_2\cos \alpha }$

$v=\frac{V_2}{q_2\cos \alpha }$

$w=-\frac{W_2}{q_2\sin \alpha }$

$\left(x\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}+1\right)\left(x\frac{\partial p}{\partial x}+y\frac{\partial p}{\partial y}\right)=\frac{{\partial }^{2}p}{\partial x^2}+\frac{{\partial }^{2}p}{\partial y^2}$   (16)

The characteristics of equation (16) are tangents to the unit circle $x^2+y^2=1$ which in $0x\text{'}y\text{'}z\text{'}$ axes becomes the cone $x{\text{'}}^2+y{\text{'}}^2=z{\text{'}}^2{\text{tan}}^2\alpha .$ The region of disturbance will therefore be bounded by cone of disturbance, the shock front and the wall of the wedge (Figure 3).

The position of the shock line referred to $\left(x,y\right)$ system is vand it will lie inside on the cone of disturbance and outside the cone of disturbance according as

$\frac{\tan \mu }{\tan \alpha }\le 1$   (17)

and $\frac{\tan \mu }{\tan \alpha }>1$    (18)

Following Chopra & Srivastava,⁷ the undisturbed part of the reflected shock lies in the plane

$x=k-y\cot {\alpha }_2\sec \mu$ , $k=\frac{\tan \mu }{\tan \alpha }$  (19)

The equation of the reflected diffracted shock may therefore be written as

$x\tan \alpha =\tan \mu -y\cot {\alpha }_2\sec \mu \tan \alpha +f\left(y\right)\sec \mu$     (20)

where $f\left(y\right)$is small

The radius of curvature $\kappa$ is given by

$\kappa$    (21)

Using equation (20), we obtain

$\kappa =\frac{f^{″}\left(y\right)\cot {\alpha }_2\cot \alpha {\text{sec}}^2\mu }{{\left(1+{\cot }^2{\alpha }_2{\text{sec}}^2\mu \right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$    (22)

Following Srivastava,⁷ we have

$\kappa =\frac{f^{″}\left(y\right)\cot {\alpha }_2\cot \alpha {\text{sec}}^2\mu }{{\left(1+{\cot }^2{\alpha }_2{\text{sec}}^2\mu \right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$    (23)

Equation (23) gives

$f^{\text{'}\text{'}\left(y\right)}=\frac{\partial v}{\partial y}.\frac{1}{\left(C_1-B_{1}y\right)}$   (24)

Combining (22) and (24) we have

$\kappa =\frac{\partial v}{\partial y}\cdot \frac{1}{\left(C_1-B_{1}y\right)}\times \frac{{\text{sec}}^2\mu \cot \alpha \cot {\alpha }_2}{{\left(1+{\cot }^2{\alpha }_2{\text{sec}}^2\mu \right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$   (25)

Following Srivastava² and Srivastava & Chopra³ we have

$\frac{\partial v}{\partial y}=\frac{C_1-B_{1}y}{C_3-B_{3}y}\cdot \frac{\partial p}{\partial y}$    (26)

From (25) and (26) we have

$\kappa =\frac{1}{C_3-B_{3}y} \frac{\partial p}{\partial y}\cdot \frac{{\text{sec}}^2\mu \cot \alpha \cot {\alpha }_2}{{\left(1+{\cot }^2{\alpha }_2{\text{sec}}^2\mu \right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$     (27)

We have the relation

$y=\kappa \left\{\cos \varphi +\sin \varphi \tan \theta \right\}$ ,$\kappa =\frac{U-q_2}{a_2}\cdot \sin {\alpha }_2$   (28)

and $\cot \varphi =\cot {\alpha }_2\cdot \sec \mu$

$\tan \theta =\frac{{\kappa }^{\prime }}{\kappa }\frac{\left(Z^2-1\right)}{\left(Z^2+1\right)}$ , ${\kappa }^{\prime }=\sqrt{1-{\kappa }^2}$    (29)

Following Chopra¹⁰ and Srivastava¹¹ the relation between Z and $z_1$ is given by

$z_1=\frac{1}{2}\left[{\left(\frac{bz+1}{bz-1}\right)}^{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}+{\left(\frac{bz+1}{bz-1}\right)}^{-\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\right]$     (30)

where $b={\left(\frac{{\kappa }^{\prime }\sin \varphi +\kappa \cos \varphi }{{\kappa }^{\prime }\sin \varphi -\kappa \cos \varphi }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$

and $\lambda ={\cot }^{-1}\left(\frac{\cot \varphi }{{\left({\sin }^2\varphi -{\kappa }^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right)$

From (30) we obtain

$z=-\frac{1}{b}\frac{\left\{1+{\left(z_1+\sqrt{z_1^2-1}\right)}^{\raisebox{1ex}{$\lambda $}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.}\right\}}{\left\{1-{\left(z_1+\sqrt{z_1^2-1}\right)}^{\raisebox{1ex}{$\lambda $}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.}\right\}}$     (31)

In (28)$z$ is substituted in terms of $z_1$ actually in terms of $x_1$ as on the real axis $y_1=0,$,$z_1$being equal to $z_1$ , we will then obtain $\frac{dy}{d{x}_1}.$

The numerical values for the calculation are

$\frac{p_0}{p_1}=0, {\alpha }_0={39.97}^0, \chi ={40}^0$

These data provide $\frac{U-q_2}{a_2}=0.94699$ (subsonic)

The solution of the problem is obtained by the introduction of the complex function

$\omega \left(z_1\right)=\frac{\partial p}{\partial x_1}-i\frac{\partial p}{\partial y_1}$   (32)

$\omega \left(z_1\right)$ is given by Chopra¹⁰

$$\omega \left(z_1\right)=\frac{G\delta \left[H\left(z_1-x_0\right)-1\right]\cos \chi \sec \alpha }{\left(z_1-x_0\right){\left(z_1^2-1\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\left(z_1-1\right)}^{\raisebox{1ex}{$\beta $}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.} e^{\varphi +i\beta }$$    (33)

where

$\varphi =\frac{z_1}{12\pi }\left[\frac{1.51716-\beta }{1}+\frac{4\left(0.00505-\beta \right)}{\left(1-0.25z_1\right)}+\frac{2\left(-0.10311-\beta \right)}{\left(1-0.50z_1\right)}+\frac{4\left(-0.22845-\beta \right)}{\left(1-0.75z_1\right)}+\frac{\left(-1.57080-\beta \right)}{\left(1-z_1\right)}\right]$   (34)

$\beta ={\tan }^{-1}{\left\{-\raisebox{1ex}{$\left(\frac{\partial p}{\partial y_1}\right)$}\!\left/ \!\raisebox{-1ex}{$\left(\frac{\partial p}{\partial x_1}\right)$}\right.\right\}}_{x_1=t=\frac{1}{x}=z_1}$  (35)

$\raisebox{1ex}{$\left(\frac{\partial p}{\partial y_1}\right)$}\!\left/ \!\raisebox{-1ex}{$\left(\frac{\partial p}{\partial x_1}\right)$}\right.=\frac{0.16931-0.09429\tan \theta -0.05812{\tan }^2\theta +0.02859{\tan }^3\theta }{{\left(0.75607-0.24393{\tan }^2\theta \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\times \left(0.36323+0.11275\tan \theta -0.06569{\tan }^2\theta \right)}$   (36)

The curvature $\kappa$from (27) can be put in the form

$\kappa =-\frac{1}{C_3-B_{3}y}\cdot \frac{\partial p}{\partial x_1}\cdot \frac{\partial x_1}{\partial y}\cdot \frac{{\sec }^2\mu \cot \alpha \cot {\alpha }_2}{{\left(1+{\cot }^2{\alpha }_2{\sec }^2\mu \right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$   (37)

On the shock from $z_1=x_1+i{y}_1=x_1$ ($z_1=x_1+i{y}_1=x_1$ being zero) and varies from $x_1=1$ to $x_1=\infty$ .

The real part on the right hand side of 33 with $z_1$ replaced by $x_1$ gives the value of $\frac{\partial p}{\partial x_1}$ .

As mentioned earlier $\frac{dy}{d{x}_1}$ is obtained from (28). Now that $\frac{\partial p}{\partial x_1}$ is known and $\frac{dy}{d{x}_1}$ is known then from (37) $\kappa$ is known. We therefore have obtained final expression for $\kappa$ .

We have the relation $\tan \theta =\frac{{\kappa }^{\prime }}{\kappa } \frac{\left(z^2-1\right)}{\left(z^2+1\right)}$ when $z\to \infty , \tan \theta =\frac{{\kappa }^{\prime }}{\kappa }$ .

So from the relation (28)$y=\kappa \left(\cos \varphi +\sin \varphi \frac{{\kappa }^{\prime }}{\kappa } \right)=\kappa \cos \varphi +{\kappa }^{\prime }\sin \varphi$

So $\frac{y}{\left(\kappa \cos \varphi +\sin \varphi {\kappa }^{\text{'}}\right)}=1$

when $\frac{y}{\left(\kappa \cos \varphi +\sin \varphi {\kappa }^{\text{'}}\right)}=1$ , then we have

$\tan \theta =\frac{{\kappa }^{\prime }}{\kappa } \frac{\left(1-b^2\right)}{\left(1+b^2\right)}=-\cot \varphi$

We have then $y=\kappa \left\{\cos \varphi +\sin \varphi \left(-\cot \varphi \right)\right\}=0$

or$\frac{y}{\left(\kappa \cos \varphi +\sin \varphi {\kappa }^{\text{'}}\right)}=0$  

So in the final analysis $z\to \infty$ ($z_1\to 1$ i.e. $x_1\to 1$ )

$\frac{y}{\left(\kappa \cos \varphi + {\kappa }^{\text{'}}\sin \varphi \right)}=1$  

and $z_1\to \frac{1}{b} \left(z_1\to \infty , x_1\to \infty \right)$   

$\frac{y}{\left(\kappa \cos \alpha + {\kappa }^{\text{'}}\sin \varphi \right)}=0$ 

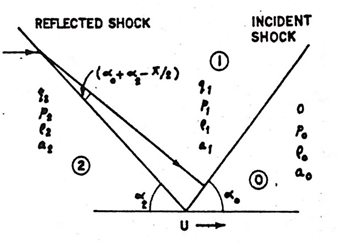
Figure 1 Oblique shock configuration.

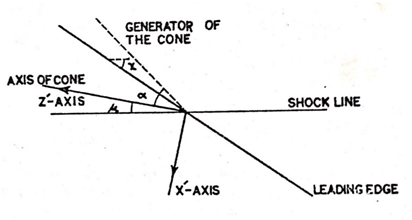
Figure 2 Configuration after interaction in the x′-z′ plane

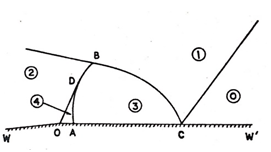
Figure 3 Flow picture in a plane perpendicular to the axis of the cone of disturbance.

Taking $\frac{\partial p}{\partial x_1}$ into consideration from equation (33) it could be seen that $\kappa$ is zero at $x_1=1$  (see equation 38) i.e. at the point of intersection of shock and Mach Cone. This is physically consistent. Also at $x_1\to \infty , \kappa$ tends to $\infty$ i.e. at the point of intersection of wall surface of the wedge and shock front intersection.

Referring to equation (33) we see that the point of inflexion over the curvature of the reflected diffracted shock is given by when

$H\left(x_1-x_0\right)-1=0$     (38)

$x_1=x_0+\frac{1}{H}$    (39)

From the calculation we have (Chopra10)

$x_1=2.71935$

The results obtained here give more general results as intersection is considered with yawed wedges. The results when there is no yaw in the wedge will reduce to the results of paper (2). The results are general and could be used in aeronautics depending on the situations that arise.

None.

The authors declare that there is no conflict of interest.

1. Lighthill MJ. The diffraction of blast-1. Proc Roy Soc A. 1949;198(1055):454‒470.
2. Srivastava RS. Diffraction of blast wave for the oblique case. London: Aeronautical Research Council; 1968. 28 p.
3. Srivastava RS, Chopra MG. Diffraction of blast wave for the oblique case. J Fluid Mech. 1970;40(4):821‒831.
4. Srivastava RS. Diffraction of oblique shock wave past a bend of small angle. International Journal of Science Technology and Management. 2016;5(1):199‒206.
5. Srivastava RS. Diffraction of oblique shock wave past a bend of small angle (subsonic case). International Journal of Advance Research in Science and Engineering. 2017;6(10):103‒108.
6. Chester W. Diffraction and Reflection of Shocks. Quarterly Journal of Mechanics and Applied Mathematics. 1954;7(1):57‒82.
7. Chopra MG, Srivastava RS. Reflection and diffraction of shocks interacted by yawed wedges. Proc Roy Soc A. 1972;330(1582): 319‒330.
8. Srivastava RS. Starting point of curvature for reflected diffracted shock wave. AIAA J. 1995;33:2230‒2231.
9. Srivastava RS. On the starting point of curvature for reflected diffracted shock wave (subsonic and sonic cases). Shock waves. 2003;13(4):323‒326.
10. Chopra MG. Pressure distribution on a yawed wedge, Interacted by an oblique shock. AIAA J. 1972;10(7):940‒942.
11. Srivastava RS. Interaction of shock waves. Netherlands: Kluwer Academic Publishers; 1994.