The theoretical model of calculation is generated and analytical dependences of the limiting heat transfer and hydraulic resistance for a flat channel with two-sided heating are obtained depending on the flow conditions of the coolant and also the boundary conditions of heat exchange, which allows to reveal the maximum reserves of heat exchange intensification in heat exchangers with flat channels for various branches of engineering production.

Keywords: limiting, intensification, heat exchange, turbulence, pipe, mathematical modeling

Intensification of heat exchange by turbulence of a flow does not require essential increase of the external sizes of flat channels and consequently is applicable in any flat channels. The manufacturing turbulizers on an outside surface of pipes is not connected to significant technological difficulties. The circuit intensification of heat exchange for the flat channel by means of turbulizers is shown in a Figure 1.

The bottom surface of the flat channel (Figure 1) we shall be by analogy to the ring channel will name conditionally internal, and top-outside. Turbulizers are established on an internal pipe. The modeling of limiting isothermal heat exchange and resistance at turbulent current in flat channels for the account turbulent of a flow is made on a technique to a similar technique applied for round pipes^1,2 and ring channels^3,4 with turbulizers. At modeling limiting heat exchange for the flat channel, intensification by means of periodically located superficial turbulizers all assumptions used at account of limiting heat exchange for round pipes and ring channels with turbulizers (except for an assumption of a hypothesis about limiting radius of the maximal speed) will be fair. At intensification of heat exchange height of the maximal speed in the flat channel (Figure 1 ), intensive by means of periodically located superficial turbulizers, is displaced in the party of a surface, with smaller factor of resistance.⁵

The situation of height of the maximal speed is determined with an average error up to 0,5% (maximal divergence has made less than 2%) empirical formula received on the basis of processing of experimental data:⁵

$Y_{\max }=\frac{y_{\max }}{Н}=\frac{1}{2}{\left(\frac{{\xi }_{}}{{\xi }_{sm}}\right)}^{0,287},$  (1)

where $\left(\frac{{\xi }_{}}{{\xi }_{sm}}\right)$ -the relation of hydraulic resistance of surfaces of the flat channel with turbulizers to smooth accordingly.

Factor of limiting hydraulic resistance we shall determine, proceeding from expression for mean expense of speed turbulent of a flow $\overline{w_x}$ :

$\overline{w_x}={\displaystyle \underset{0}{\overset{1}{\int }}{w}_{x}dY=}{\displaystyle \underset{0}{\overset{Y_{\max }}{\int }}{\left(w_x\right)}_{SS}dY}+{\displaystyle \underset{Y_{\max }}{\overset{1}{\int }}{\left(w_x\right)}_{TS}dY,}$   (2)

where ${\left(w_x\right)}_{SS}$ and ${\left(w_x\right)}_{ТS}$ -axial making speeds of a flow on the part of smooth and turbulent of surfaces accordingly.

Further we shall arrive the same as and for a case of modeling of limiting heat exchange in a round pipe with turbulizers;^1,2 the appropriate structures of speeds hypothetically are accepted same, as well as for a case in a pipe. After the appropriate reductions, we shall receive the nonlinear equation for limiting factor of hydraulic resistance of the flat channel:

$1=\frac{2\kappa A^2}{\mathrm{Re}}+\frac{1}{2}\left\{\frac{\sqrt{\xi }}{\sqrt{2}}B+\frac{\xi }{16\cdot \sigma }{\left(1-\frac{4A\sqrt{2}}{\sqrt{\xi }\mathrm{Re}}\right)}^2\right\}\left[1-\frac{8A\sqrt{2}}{\sqrt{\xi }\mathrm{Re}}\right]-$

$1=\frac{2\kappa A^2}{\mathrm{Re}}+\frac{1}{2}\left\{\frac{\sqrt{\xi }}{\sqrt{2}}B+\frac{\xi }{16\cdot \sigma }{\left(1-\frac{4A\sqrt{2}}{\sqrt{\xi }\mathrm{Re}}\right)}^2\right\}\left[1-\frac{8A\sqrt{2}}{\sqrt{\xi }\mathrm{Re}}\right]-$     (3)

where $A,B,\kappa ,\sigma$ -constants, determinate the same as in:^1,2 А-characterizes average border of jet area; В-characterizes factor of proportionality between longitudinal speed and speed of friction (constants А=15¸114 and В=6,5¸8,5 at change Re=10⁴¸10⁵); k=0,443-constant for a universal structure of speed in turbulent a flow; s=0,013-constant for a jet nucleus of a flow describing initial turbulence; Re-number Reynolds on an equivalent diameter of the channel; x-factor of resistance to friction for the flat channel with turbulizers.

It is accepted, that the diameter of the smooth channel is equal to a diameter of the channel carrying ribbing, and the speed of a flow was determined on section of the channel, which would be at absence ribbing. The above-stated approach to the full is lawful, as at a considered type limiting turbulent the rather low ledges are used. In the further comparative analysis will be made on an equivalent diameter of the flat channel: d_eqv=2∙H.

In Figure 2 the settlement absolute meanings of limiting factor of hydraulic resistance for the flat channel are given depending on number Reynolds, equations, received as a result of the numerical decision, (3), from which it is visible, that to increase of number Reynolds there is a fall of factor of resistance. The important parameter is relative limiting factor of hydraulic resistance for the flat channel x/x_sm, shown on a Figure 3; for comparison are given similar given for a round pipe taken from. ^1,2 The hydraulic resistance for the smooth flat channel paid off, proceeding from empirical dependences given in.⁵ From a Figure 3 the maximum of the relation is visible, that x/x_sm occurs at higher numbers Reynolds and his meaning a little bit above, than for a round pipe.

Last specifies that the limiting current for a flat pipe with turbulizers has higher relative resistance. The numerical decision of the nonlinear equation (3) for limiting factor of hydraulic resistance for the flat channel allows to determine limiting heat exchange for these conditions. Number Nusselt at the stabilized current for an internal wall Nu_1∞ the flat channel with bilateral admission of heat, agrees,^6,7 is equal:

${\text{Nu}}_{1\infty }=\langle \frac{1}{2}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{{\left({\displaystyle \underset{0}{\overset{Y}{\int }}\frac{w_x}{\overline{w_x}}dY-1}\right)}^2}{\left(1+\frac{\mathrm{Pr}}{{\mathrm{Pr}}_T}\frac{{\mu }_T}{\mu }\right)}}dY+{\frac{1}{2}\frac{q_{с2}}{q_{с1}}{\displaystyle \underset{0}{\overset{1}{\int }}\left\{\frac{\left({\displaystyle \underset{0}{\overset{Y}{\int }}\frac{w_x}{\overline{w_x}}dY-1}\right)}{\left(1+\frac{\mathrm{Pr}}{{\mathrm{Pr}}_T}\frac{{\mu }_T}{\mu }\right)}\left[{\displaystyle \underset{0}{\overset{Y}{\int }}\frac{w_x}{\overline{w_x}}dY}\right]\right\}}dY\rangle }^{-1},$  (4)

where $\mathrm{Pr}$ -number Prandtl; ${\mathrm{Pr}}_{Т}$ -turbulent number Prandtl; $$\mu$$ -Dynamic viscosity;${\mu }_{Т}$ -turbulent dynamic viscosity; $\left(\frac{q_{c2}}{q_{c1}}\right)$ -the given relation of thermal flows at outside and internal heating accordingly.

Thus, for account of limiting heat exchange in the flat channel with turbulizers it is necessary to determine integrals contained in (4), for all channel. For this purpose the flat channel is broken into three sub-layer from each of the parties, i.e. is simulated hexa-layer by the circuit turbulent of a boundary layer: for smooth and intensification of the parties-viscous sub-layer, intermediate sub-layer, turbulent a nucleus. At account of limiting heat exchange for a round pipe with turbulizers in^6,7 use of an assumption was shown, that $\frac{w_x}{\overline{w_x}}\cong 1$ , the precisely same conclusion rather insignificantly influences final result of account of heat exchange-it is possible to make and for limiting heat exchange for conditions of the flat channel with turbulizers. Hence, the opportunity of the analytical decision of a task about limiting heat exchange for the flat channel with turbulizers with bilateral admission of heat takes place; according to principle additions, expression for integrals which are included in the right part of expression (4), for each of appropriate sub-layer $I_i$ will accept a kind:

${\text{Nu}}_{\text{1}\infty }=\frac{1}{{\displaystyle \sum _{i=1}^6{I}_i}};$      (5)

where by an index "i" are designated: 1, 2, 3-viscous sub-layer, intermediate sub-layer, turbulent a nucleus accordingly for internal (which surface intensive) surface of the flat channel; 4, 5, 6-turbulent a nucleus, intermediate sub-layer, viscous sub-layer accordingly for outside (which surface smooth) surface of the flat channel.

After calculation of the given integrals, analytical dependences for $I_i$ $\left(\forall i=1÷6\right)$ in (5) after calculation of the given integrals, analytical dependences for:

$I_1=\frac{2\sqrt{2}}{\mathrm{Re}\sqrt{\xi }}\left\{\frac{2304}{{\mathrm{Re}}^2\xi }\left(\frac{q_{c2}}{q_{c1}}+1\right)-\frac{72\sqrt{2}}{\mathrm{Re}\sqrt{\xi }}\frac{q_{c2}}{q_{c1}}-\frac{144\sqrt{2}}{\mathrm{Re}\sqrt{\xi }}+6\right\};$   (6)

$I_2=\frac{2{\mathrm{Pr}}_{T}B}{3\mathrm{Re}\xi \left({\mathrm{Pr}}_{T}B+\mathrm{Pr}A\right)}[\frac{32\sqrt{2}{A}^3}{\sqrt{\xi }}\left(\frac{q_{c2}}{q_{c1}}+1\right)-24A^2\mathrm{Re}-12A^2\mathrm{Re}\frac{q_{c2}}{q_{c1}}+$   (7)

$$+3\sqrt{2}A{\mathrm{Re}}^2\sqrt{\xi }-18\sqrt{2}{\mathrm{Re}}^2\sqrt{\xi }+864\mathrm{Re}+432\mathrm{Re}\frac{q_{c2}}{q_{c1}}-\frac{6912\sqrt{2}}{\sqrt{\xi }}\frac{q_{c2}}{q_{c1}}-\frac{6912\sqrt{2}}{\sqrt{\xi }}]$$

$I_3+I_4=\left(\frac{1}{12}-\frac{10}{\mathrm{Re}\sqrt{\xi }}\sqrt{2}-\frac{1}{3}\frac{A}{\mathrm{Re}\sqrt{\xi }}\sqrt{2}\right)/\left(1+\sigma \mathrm{Re}\frac{\mathrm{Pr}}{{\mathrm{Pr}}_T}\right)\times$ 

$\times [\frac{64A^2}{{\mathrm{Re}}^2\xi }\left(\frac{q_{c2}}{q_{c1}}+1\right)-\frac{1920A}{{\mathrm{Re}}^2\xi }\left(\frac{q_{c2}}{q_{c1}}+1\right)+\frac{57600}{{\mathrm{Re}}^2\xi }\left(\frac{q_{c2}}{q_{c1}}+1\right)-$ 

$-\frac{16A\sqrt{2}}{\mathrm{Re}\sqrt{\xi }}-\frac{4A\sqrt{2}}{\mathrm{Re}\sqrt{\xi }}\frac{q_{c2}}{q_{c1}}-\frac{120\sqrt{2}}{\mathrm{Re}\sqrt{\xi }}\frac{q_{c2}}{q_{c1}}+\frac{240\sqrt{2}}{\mathrm{Re}\sqrt{\xi }}-\frac{q_{c2}}{q_{c1}}+2$   (8)

$I_5=\left(2304/\left(1+\frac{\mathrm{Pr}}{{\mathrm{Pr}}_T}\frac{A}{B}\right)\right)\frac{1}{{\mathrm{Re}}^2\xi }\left[\frac{62}{\mathrm{Re}}\sqrt{\frac{32}{\xi }}\left(\frac{q_{c2}}{q_{c1}}+1\right)-3\frac{q_{c2}}{q_{c1}}\right]$   (9)

$I_6=\frac{4608\sqrt{2}}{{\mathrm{Re}}^3{\xi }^{\frac{3}{2}}}$     (10)

The settlement importance of limiting numbers Nusselt for Pr=0,72 and Pr=10 depending on number Reynolds are given in a Figure 4.

Hence, from the point of view of limiting turbulence greatest intensification takes place for a round pipe with turbulizers, for the flat channel with turbulizers on one of surfaces intensification of heat exchange is lower, it is even lower for the ring channel with turbulizers on an internal wall. After comparison of the theoretical data on limiting heat exchange for the flat channel with the theoretical data for a round pipe,^1,2 and also with the ring channel,^3,4 it is necessary to proceed to comparison it with the appropriate existing experimental data. Most suitable for the above-stated comparison are the experimental data given in.⁵ In work,⁵ it is underlined, that the existing experimental data allow, at saturation intensification of heat exchange occurring in a case, when turbulizers fall outside the limits laminar and transitive layers, to reach meanings of growth heat irradiation in 2¸2,8 times at growth of hydraulic resistance in 3,35¸6 times,⁵ while the theoretical importance of limiting heat exchange received on a technique, developed within the framework of the given work, is equal 2,9. Hence, the theoretical data well correlating with experimental, specify that at the given method intensification of heat exchange his reserves are revealed almost all. In a Figure 6 relative limiting heat exchanges ${\text{Nu }}_{\text{1}\infty }{\text{/Nu}}_{\text{1}\infty \text{sm}}$ at bilateral heating for flat channel and for ring channel with R₁=½ with other things being equal (Re=10⁴; Pr=0,72) is resulted depending on the attitude of thermal flows at outside and internal heating accordingly $\left(\frac{q_{c2}}{q_{c1}}\right)$ . From a Figure 7 the heating of an outside wall is clearly visible, that $\left(\frac{q_{c2}}{q_{c1}}\uparrow \right)$ essentially reduces relative limiting heat exchange $${\text{Nu }}_{\text{1}\infty }{\text{/Nu}}_{\text{1}\infty \text{sm}}$$ on an internal surface, i.e. the surfaces, on which are located turbulizers, both for the flat channel, and for the ring channel. Decrease of limiting relative heat exchangefor flat channel atoccurs a little bit more poorly, than for the ring channel, therefore in this respect flat channel more preferably ring. Hence, maximal limiting heat exchange ${\text{Nu }}_{\text{1}\infty }{\text{/Nu}}_{\text{1}\infty \text{sm}}$ for the flat channel $\left(\frac{q_{c2}}{q_{c1}}\uparrow \right)$ can be received at unilateral heating $\left(\frac{q_{c2}}{q_{c1}}\to 0\right)$ . In the given research the cases with negative importance are not considered $\left(\frac{q_{c2}}{q_{c1}}\right)$ .

After consideration of influence on limiting heat exchange in the flat channel with turbulizers on an internal surface of a mode of current of the heat-carrier (Figure 5), boundary conditions of heat exchange (Figure 6), is necessary to consider his(its) dependence on Prandtl number. In a Figure 77 the dependence of limiting heat exchange in the flat channel with turbulizers on an internal surface is given at heating only of internal wall ${\text{Nu }}_{\text{11}\infty }{\text{/Nu}}_{\text{11}\infty }{}_{\text{sm}}$ depending on Prandtl number at the fixed number Reynolds Re=10⁴; the settlement data for other numbers Reynolds have similar character.

For comparison the appropriate data on relative limiting heat exchange are given ${\text{Nu }}_{\text{11}\infty }{\text{/Nu}}_{\text{11}\infty }{}_{\text{sm}}$ for ring channel with turbulizers on internal pipe with R₁=½ and for a round pipe with turbulizers ${\text{(Nu }}_{\infty }{\text{/Nu}}_{\infty \text{sm}}\text{)}$ with other things being equal (Re=10⁴). The analysis of the data on limiting heat exchange depending on Prandtl number, submitted on a Figure 7, shows, that relative limiting heat exchange ${\text{Nu }}_{\text{11}\infty }{\text{/Nu}}_{\text{11}\infty }{}_{\text{sm}}$ the analysis of the data on limiting heat exchange depending on number Prandtl, submitted on a Figure 7, shows, that the relative limiting heat exchange for the flat channel with turbulizers is rather sharply reduced with increase of number Prandtl. The decrease of relative limiting heat exchange is obvious, that ${\text{Nu }}_{\text{11}\infty }{\text{/Nu}}_{\text{11}\infty }{}_{\text{sm}}$ for the flat channel at increase of number Prandtl occurs much faster, than for a round pipe and practically the same as for the ring channel with turbulizers on an internal pipe. The greatest meanings of limiting relative heat exchange for the flat channel, as well as in case of limiting heat exchange for a round pipe, are in area gasiform of heat-carriers. The reduction of relative limiting heat exchange is obvious, that b${\text{Nu }}_{\text{11}\infty }{\text{/Nu}}_{\text{11}\infty }{}_{\text{sm}}$ for the flat channel at increase of number Prandtl occurs much faster, than for a round pipe and practically the same as for the ring channel with turbulizers on an internal pipe. Hence, the round pipe with turbulizers has advantage for intensification of heat exchange at higher numbers Prandtl not only above ring channels with turbulizers on an internal pipe,^3,4 but also above flat channels with turbulizers on an internal surface. The important parameter of dependence limiting intensification of heat exchange for various channels from number Prandtl is such this number, at which limiting intensification becomes to equal unit.

For example,${\left({\text{Nu}}_{\infty }{\text{/Nu}}_{\infty \text{sm}}\right)|}_{\max }=1,00$ at Pr=85,6 (at use for account ${\text{Nu}}_{\infty \text{sm}}$ the formulas Dittus–Bolter). Relevant it is necessary to note, that meanings $${\left({\text{Nu}}_{\text{11}\infty }{\text{/Nu}}_{\text{11}\infty \text{sm}}\right)|}_{\max }$$ and ${\left({\text{Nu}}_{\infty }{\text{/Nu}}_{\infty \text{sm}}\right)|}_{\max }$ are realized at various numbers Reynolds for different channels.

For the ring channel with turbulizers on an internal pipeis ${\left({\text{Nu}}_{\text{11}\infty }{\text{/Nu}}_{\text{11}\infty \text{sm}}\right)|}_{\max }=1,00$ reached at Pr=11,6 for R₁=¾; at Pr=7,9 for R₁=½ and at Pr=7,5 for R₁=¼. For the flat channel with turbulizers on an internal surface at unilateral heating ${\left({\text{Nu}}_{\infty }{\text{/Nu}}_{\infty \text{sm}}\right)|}_{\max }=1,00$ is achieved at Pr=17,3. Hence, for flat channels limiting intensification of heat exchange is possible at higher numbers Prandtl, than for ring channels, but also on this parameter they as concede to round pipes. In works^1,2 was theoretically proved, that for round pipes with turbulizers in case of limiting heat exchange in the certain area of numbers Reynolds $\mathrm{Re}\approx \left(1÷2\right)\cdot {10}^4$ carry of heat prevails above carry of a pulse, and then, down to $\mathrm{Re}\approx 5\cdot {10}^4$ , the carry of heat becomes smaller, than carry of a pulse; then the distinction between them is reduced.^1,2 The developed above technique of account of limiting heat exchange and hydraulic resistance for flat channels with turbulizers allows to construct for them similar law.

The specified law for air is reflected in a Figure 8, where the dependence is shown:

$\Xi (\mathrm{Re})=:\frac{{\text{Nu}}_{\text{11}\infty }{\text{ /Nu}}_{\text{11}\infty }{}_{\text{sm}}}{\xi \text{ /}{\xi }_{\text{sm}}}\left(\mathrm{Re}\right)$     (11)

For comparison are given appropriate given for a round pipe with turbulizers.^1,2 From a Figure 8 parameter is visible, that Ξ for the flat channel makes much smaller size, than for a round pipe.

Last specifies that the round pipe has advantage from the point of view of limiting intensification of heat exchange in comparison with the flat channel. Besides for flat channel already is not present areas with prevalence of carry of heat above carry of a pulse, and also is absent area of decreases of prevalence of carry of a pulse above carry of heat (at approximation to $\mathrm{Re}\approx {10}^5$ importance Ξ only are somewhat stabilized), that is characteristic for a round pipe. Last is an additional reason for a reduction of the flat channel in relation to a round pipe. Last specifies that the round pipe has advantage from the point of view of limiting intensification of heat exchange in comparison with the flat channel. Besides for the flat channel already there are no areas with prevalence of carry of heat over carry of a pulse, and also there is no area of reduction of prevalence of carry of a pulse above carry of heat (at approximation to $\mathrm{Re}\approx {10}^5$ importance Ξ only are somewhat stabilized), that is characteristic for a round pipe. Last is an additional reason for a reduction of the flat channel in relation to a round pipe. The urgency of a problem intensification of heat exchange in modern metallurgical manufacture, was most in detail shown in the monographies,^8‒13 where it was specified on advantage of theoretical research intensification of heat exchange above experimental. The theoretical research intensification of heat exchange in heat exchangers for metallurgical manufacture is based on available development in this area,^8‒13 which successfully proceed now.

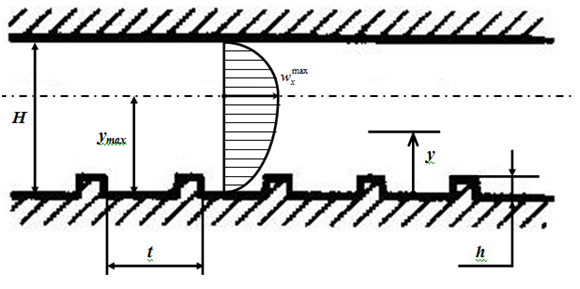
Figure 1 Cross section of the flat channel with turbulizers.

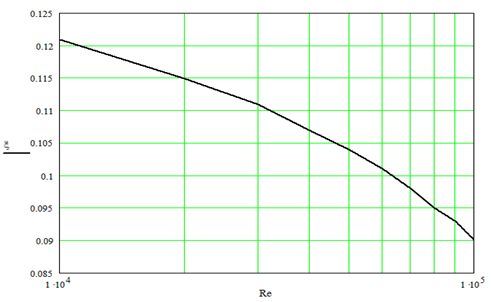
Figure 2 Absolute meanings of limiting factor of hydraulic resistance for the flat channel depending on number Reynolds.

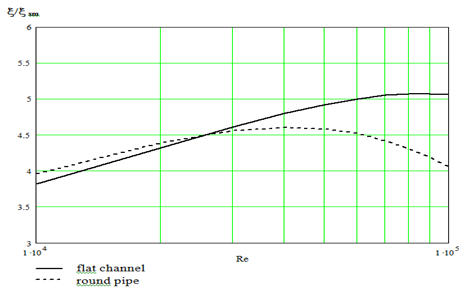
Figure 3 Meanings of the relations of limiting factor of hydraulic resistance for the flat channel to the appropriate smooth channel x/xsm depending on number Reynolds (for comparison the similar ratio for a round pipe) are given.

Figure 4 Absolute meanings of limiting numbers Nusselt for Pr=0,72 and Pr=10 for the flat channel depending on number Reynolds.

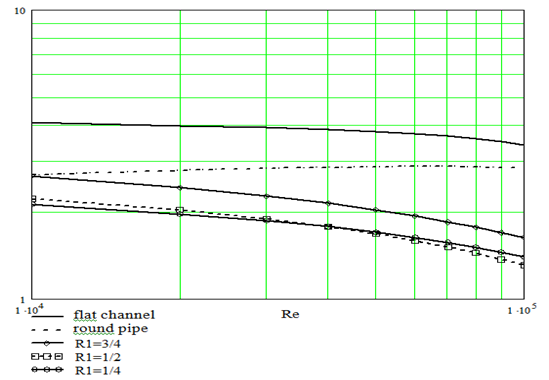
Figure 5 Settlement meanings of limiting relative heat exchange $N{u}_{11\infty }/N{u}_{\text{11}\infty \text{sm}}$ for air in the flat channel with turbulizers on an internal surface at heating only of internal wall depending on Re.

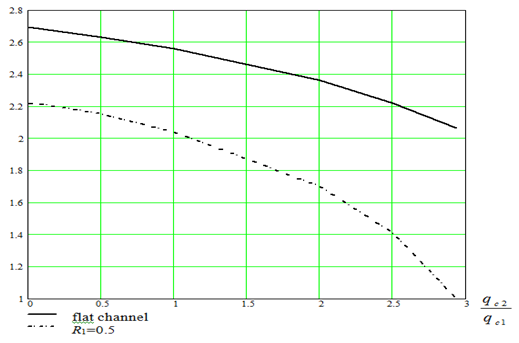
Figure 6 Relative limiting heat exchange $N{u}_{11\infty }/N{u}_{\text{11}\infty \text{sm}}$ at bilateral heating for flat channel and for ring channel with R₁=½ with other things being equal (Re=10⁴; Pr=0.72) depending on the attitude of thermal flows at outside and internal heating accordingly $\left(\frac{q_{c2}}{q_{c1}}\right)$ .

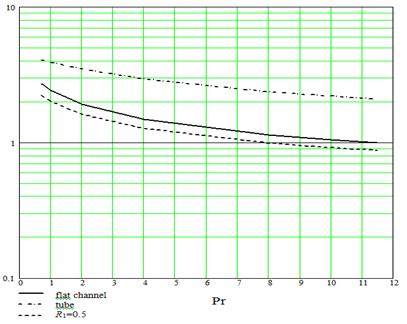
Figure 7 Dependence of limiting heat exchange in the flat channel with turbulizers on an internal surface at heating only of internal wall$N{u}_{11\infty }/N{u}_{\text{11}\infty \text{sm}}$ from Prandtl number (for comparison are given appropriate given for a round pipe and for the ring channel with R₁=½).

Figure 8 Dependence of parameter X at Re=10⁴ and Pr=0,72 for the flat channel with turbulizers on an internal surface at unilateral heating (for comparison are given similar given for a round pipe with turbulizers).

1. The theoretical model of account is developed and the analytical dependences of limiting heat exchange and hydraulic resistance for the flat channel with bilateral heating are received depending on modes of current of the heat-carrier, and also boundary conditions of heat exchange. Intensification is received by means of periodically located superficial turbulizers on an internal surface.
2. The importance of relative limiting heat exchange for flat channels are a little bit higher, than ring and is always lower, than for a round pipe.
3. For flat channels the limiting carry of heat cannot prevail above carry of a pulse, while for round pipes in the certain area of numbers Reynolds it is possible.
4. The generated theory allows revealing the maximal reserves intensification of heat exchange in ceramic heat exchangers with flat channels for modern metallurgical manufacture.

None.

The author declares that there is no conflict of interest.

1. Dreitser GA, Lobanov IE. Research limiting intensification of heat exchange in pipes at the expense of artificial turbulence of a flow. Heatphysics of high temperatures. 2002;40(6):958‒963.
2. Dreitser GA, Lobanov IE. Limiting intensification of heat exchange in pipes at the expense of artificial turbulence of a flow. Engineering physical magazine. 2003;76(1):46‒51.
3. Dreitser GA, Lobanov IE. Modeling of limiting heat exchange turbulence of a flow in ring channels. News of high schools: Air engineering. 2004;4:44‒48.
4. Lobanov IE. Modeling of limiting heat exchange by means of turbulence of a flow for ring channels. Kazan: Problems heat- and mass exchange and hydrodynamics in power- and mechanical engineering works; 2004. 134‒142 p.
5. Kаlinin EK, Dreitser GA, Kоpp IZ, et al. Effective surfaces of heat exchange. Moscow: Energoatomizdat; 1998. 408 p.
6. Novikov II, Voskresenskij KD. Applied thermodynamics and heat transfer. Moscow: Аtomizdat; 1977. 349 p.
7. Petuhov BS, Genin LG, Kоvaljov SA. Heat exchange in nuclear power installations. Moscow: Energoatomizdat; 1986. 470 p.
8. Lobanov IE. Mathematical modeling intensification of heat exchange at turbulent current in channels. Moscow: The dissertation on competition of a scientific degree of the doctor of engineering science; 2005. 632 p.
9. Lobanov IE, Dotsenko АI. Mathematical modeling of limiting heat exchange for turbulence of a flow in channels. Moscow: МIKH&S; 2008. 194 p.
10. Lobanov IE, Stein LМ. Mathematical modeling intensification of heat exchange at turbulent current in channels with application of the basic analytical and numerical methods. Moscow: Publishing house of association of building high schools; 2009. 405 p.
11. Lobanov IE, Stein LМ. Mathematical modeling intensification of heat exchange at turbulent current in channels with application of the not basic analytical and numerical methods. Moscow: Publishing house of association of building high schools; 2010. 290 p.
12. Lobanov IE, Stein LМ. Mathematical modeling intensification of heat exchange at turbulent current in channels with application multi-layer, super-multi-layer and compound of models turbulent of a boundary layer. Moscow: МGАKH&S; 2010. 288 p.
13. Lobanov IE, Stein LМ. Special aspects of mathematical modeling hydrogasodynamics, heat exchange, and also heat transfer in heat exchange devices with intensification by heat exchange. Moscow: МGАKH&S; 2011. 343 p.