Due to the increased trends and innovation with reliable IoT sensors, high-speed networks, and supercomputers the amount of data solving has improved in predicting performance with greater accuracy. Machine learning-based diagnostics and health monitoring for large gas turbines are available but lack application in Micro gas turbine component design and performance prediction. In this paper to predict the optimized net efficiency using a machine learning-based model was developed. Micro gas turbine power plant mathematical model (MGTPPMM) was developed that could generate an electric power of 6kW which was validated using the operational conditions of Jet Cat PHT3. The resulting data was used to optimize and predict the net efficiency of gas turbines and also its compressor and turbine characteristics using a Machine learning algorithm model (MLAM). The MGTPPMM has an accuracy of 92% in simulating various operating conditions while two MLAM was developed Predictor 1 and Predictor 2. Predictor 1 has an accuracy of 76% and Predictor 2 has an accuracy of just less than1 % error at sea level operating conditions. However at higher altitudes greater than 17 Km operating condition the accuracy of the MGTPPMM is 88% while that of the MLAM - Predictor 2 has an error of less than 6% this is due to the lack of sufficient validated results data required for training sets. The proposed models may help to design more efficient micro gas turbines at the component level and also could predict performance characteristics to monitor the health of the system virtually by implementing a degradation monitor system.

Keywords: micro gas turbine, machine learning, performance prediction, efficiency optimization, power plants, components design, deep learning

The explosion of data along with cheap computing component devices has made large strides in the mathematical modeling based evaluations. Data can be extracted both in real-time or based on computer simulations. The simulated data have different degrees of accuracy as the theoretical components are not 100% ideal whereas the real data also has varying degrees of accuracy due to the noise, interference, and the sensor's faulty response. So assuming field data, operating data, and the simulated data all have some degree of deviations from the actual predicted parameters. Gas turbine is one of the internal combustion engines that couples an upstream and a downstream rotating compressor and turbines together. These engines have high efficiency and reliability supporting high energy density power requirements. Due to the high cost of operating data in this article simulated data has been used for the added advantage. The physics-based model should be validated for operating condition simulations. The data are extracted from the in house software ASTRA developed at Samara University.¹

ASTRA is used in the aerospace field for generating high fidelity computer simulations using complex physics-based engineering models for designing components to predict their performances. The system has been validated with numerous gas turbines. The goal of optimizing data helps in designing components with improved accuracy thus increasing the performance of the Micro gas turbine power plant (MGPT).Artificial intelligence refers to the learning process of machines to predict the performance of gas turbines (GT) for completing the missing experimental data, and for evaluating different ambient conditions, and also for predicting emissions.^2,3 Lots of research has been investigated using genetic algorithms or Fuzzy logic for power plant size greater than 1 megawatt for evaluating and predicting machine behavior during its operations. Studies were made for fuel importance,³ for the diagnosis of faults arising in a turbofan engine,⁴ preventive maintenance optimization,⁵ and also for multivariable control system control systems.^6,7

Based on the state variable method a mathematical model for a Jet Cat PhT3 was developed. The goal was to obtain maximum overall efficiency with minimum viable Turbine inlet temperature (TiT) was optimized and the obtained value was validated. The model is dynamic that captures both the steady and transient behavioral state of the power plant. The simulated results from the ASTRA are found to be in good agreement with the experimental data of Pht3 Jet cat.⁸ The block diagram of the Jet Cat pht3 power plant is given in figure 1. A component-oriented basis model was developed to act as a Micro gas turbine power plant mathematical model (MGTPPMM) as shown in figure 2. The description of the components helps in matching the components for obtaining a functional power plant. The equations representing the gas turbine models could be found here for further explanation and validation.^9-11

Figure 1 The block diagram of the Jet Cat pht3 power plant.

Figure 2 Micro gas turbine power plant mathematical model (MGTPPMM).

This research deals with the optimization of the gas turbine efficiency focused on Pressure ratio and Cycle Peak Temperature. Evaluation of data in batches of even thousands can rapidly be investigated to explore the best design. This evaluation process of design by varying parameters is Parametric Analysis. The features considered for designing the MGTPPMM are elaborated in the table 1. The ambient parameters used are globally accepted standard at sea level data gathered from the ISO standards 3977-2, the ISO ambient conditions for the industrial gas turbine. This data and information involves the density of the air. Any deviation in the standards of the ISO would have an impact on the density of the air. This would affect the results due to the change in the mass flow rate, the amount of air that enters the gas turbine system. The station numbering of the power plant is taken from.¹² The table 2 consist of the various design input parameters into the MGTPPMM.

Modeling and simulation has been used to solve the problems of complex systems. The three most important techniques that are used are white box, black box, and the gray box. White-box modeling is based on first principles and analytical models whereas black-box modeling is a statistic modeling driven by empirical models. The gray-box based modeling is a combination of both the white and black box.¹³ Modeling and simulation helps to understand the target function with variable parameters for evaluating the performance of the system. Due to the vast availability of data, the researchers move to the data-modeling approach. The proposed gray-box model achieves a more accurate prediction to provide a new possibility for modeling and simulation. This helps with non-linear functions and could deal with uncertainty and ambiguous information. The functions are mapped nonlinearly with Turbine inlet temperature TiT (k) from an input vector to an output scalar.

The model has five inputs, namely, isentropic turbine efficiency( ), isentropic compressor efficiency ( ), ambient temperature ( ), pressure ratio (PR), and turbine inlet temperature (TiT), as well as three outputs, fuel consumption, power output, and overall efficiency. The complexity of aerothermodynamics analysis makes it impossible to mathematically solve the optimization equations involved in various gas turbine cycles. The effects of different parameters have been analyzed to select the optimum gas-turbine configuration to reach high efficiency. The system represents as proposed in the reference.¹⁴

Fn: n f XR Z R

There are numerous methods to solving this problem but here to deal with complex patterns visualizing through statistical methods. The efficiency prediction problem could be modeled as the input 𝑋={𝑥1…𝑥𝑁} that has a of 𝑁 features. Here the Features identified as the pressure ratio and Turbine Inlet Temperature. The result 𝑌 is predicted to be the optimized solution of the problem for the input 𝑋.

The 𝑌′ is the solution that is returned by various models based on the object given as input for learning called the training set. Two MLAM-Predictor 1 and Predictor 2 were developed to predict the operating conditions which are associated with the performance enhancement of the gas-turbine power plant by obtaining the overall. The approaches considered were the sparse model for linear regression estimation (Predictor 1) and Random Forest Decision Tree (Predictor 2) due to their various benefits mentioned in numerous researches.^15-17 

Predictor 1-Linear regression is a statistical approach where a target function 𝐹 is linear and depends on features as the input. All input attributes as real numbers and represented as:

(𝑥) = 𝑎0 + ∑ 𝑎𝑖𝑥𝑖𝑁𝑖=1.

Where, 𝑎𝑖 is a coefficient, 𝑥𝑖 is a parameter (feature), 𝑁 is severaparameters.

Predictor 2-Random Forest Decision Tree is developed using a set of rules and conditions for the input features and operation outcomes which results in optimized results. The input features are constructed using the training set. The model uses a bagging method and probability mechanism.

The multiple regression objective results in understanding the relationships between several predictors and an outcome variable. The data has been cleaned and segregated with a classification problem where overall efficiency is considered to be predicted as shown in table 3 filter method is required to clean the data and to identify the subset of variables for correlation analysis.

The computational problem would require fitting a regression equation to the training data. The data contains 256 data points collected from a Jet cat PhT3 power plant with an output fixed power of 6 kW. The features set are the Mass flow rate of the inlet air ( m), Pressure ratio (PR) and Turbine Inlet Temperature (TiT) for predicting the Overall efficiency (n_e ). The model uses a Rule-based algorithm for the regression model to make decisions for predicting the category of the overall efficiency.

The performance prediction based on the simulated power plant data. This process is commonly referred to as data-based performance adaptation and deals with the optimization of component-based parameters such as mass flow and overall efficiency in comparison with the Turbine inlet temperature and Pressure ratio to measure and predict the gas path temperatures and pressures for matching. Here in this optimization minimization is the goal.

Micro gas turbines have an overall efficiency of 6%-10 % when producing electricity. They depend on the mass flow of the air intake to the compressor and the heat supplied to it. In this example, a Gas turbine power plant was simulated to produce a power of 6kW output power. The result is plotted in the following figures 5 & 6.

Figure 3

Figure 4 Final Optimized Cycle result for 6 kW system @ sea level.

Figure 5 The relation between overall efficiency and pressure ratio at various turbine inlet temperatures.

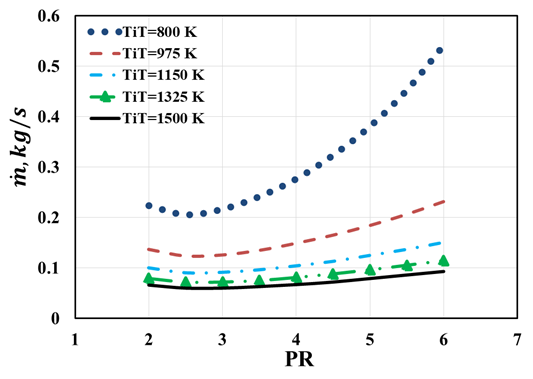
Figure 6 The relation between mass flowrate and pressure ratio at various turbine inlet temperatures.

From figures 5 & 6, the optimized pressure ratio as 3, the turbine inlet temperature as 1200 K which yields a net efficiency of 7.7% was estimated. GT efficiency is about thermal circulation that has been strongly affected by the overall profitability of electrical energy. To improve the performance of power plants with the improvement of energy productivity and the reduction in fuel consumption.

Results of Predictor 1 and 2 the data is fed into the two developed Machine language models 80% of the data have been used for training the model, the remaining 20% of the data was used to test the model accuracy for predicting our gas turbines overall efficiency. The prediction accuracy and model recovery performance of each approach are investigated for both simulated and real benchmark datasets. The sklearn models were used for both regression and Text classifier as shown in the following coding and the data were split by 80% for the training set and the remaining 20% as the test set.

Predictor 1: regressor = LinearRegression()

regressor.fit(X_train, y_train)

Predictor 1: clf = RandomForestClassifier()

clf.fit(X_train, y_train)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)

The model resulted in a score of 0.72 for LinearRegression() and 0.962 for the RandomForestClassifier(). The novelty of the concept lies in predetermining the labels for the various degrees in the overall efficiency rather than a numerical number. The regression model is faster but has a low score whereas the Random classifier has an average relative error that is less than 4% is considered as a high enough result. The preprocessing of the data gives benefits in improving the score. The prediction of the overall efficiency by the Random classifier gave good results. The results data consists of three sets classified as generated data and the predicted data. The generated data consists of the simulated value while we have two predicted data: predictor 1 (LinearRegression) and predictor 1 (LRandomForestClassifier) based on the two Machine language modules.

Figure 7 shows the result when the input is Turbine Inlet Temperature used to predict the gas turbines overall efficiency. Figure 8 shows the result when the input is the Mass flow rate used to predict the gas turbines overall efficiency. Figure 9 shows the result when the input is the Pressure ratio used to predict the gas turbines overall efficiency. In figures 7-9 all the three models and their predicted efficiency are plotted. Predictor 2 has a better response to the simulated value. In figure 10 the bar graph shows the predicting accuracy of the efficiency between the three different models. The height of the bar chart shows the values almost equal to the simulated value.

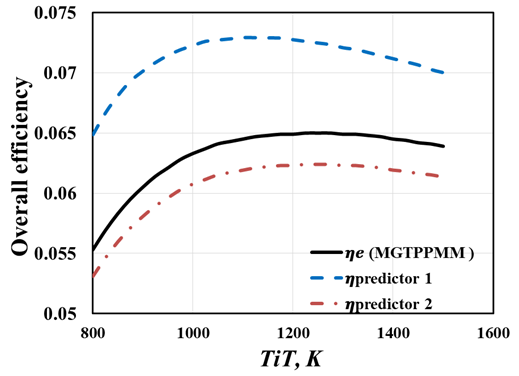
Figure 7 The relation between overall efficiency and predict efficiency on turbine inlet temperatures.

Figure 8 The relation between overall efficiency and predict efficiency on mass flowrate.

Figure 9 The relation between overall efficiency and predict efficiency on pressure ratio.

Figure 10

Figures 11, 12 & 13 show the statistical data convergence and dispersions from the center mean at which the system could predict the Overall efficiency of the power plant. These scatter plots help us to clean the data and process them in a better way to increase the sensitivity of the AI system. In figure 12 the red line acts as an ideal data point for achieving better accuracy in predicting the output. Thus data filter and data cleaning before performing the model training are highly recommended.

Figure 11

Figure 12

Figure 13

This paper reviewed the thermodynamic principles of single shaft gas turbines and discussed the cycle characteristics of the model presented as MGTPPMM. They have been verified with the Jet Cat pht3 lab model. Two data-based efficiency predictor linear regression estimation (Predictor 1) and Random Forest Decision Tree (Predictor 2) were developed. Among the predictors, Random Forest Decision Tree is better in terms of Accuracy score and has better quality of the overall efficiency predicted as close to the data simulated. In the future, k-means clustering or other such models can be used to check the prediction accuracy. Even hybrid models could be incorporated. The models in the future could be able to work even in an unlabeled data environment. Here multi-label Semi-supervised learning methods were proposed and their results were explained. The simulation tool ASTRA data output could be used to create the training data set for the Artificial neural network (ANN). The ANN consists of several neurons that are processing units between layers. The gas paths are depicted as the layers. These models are described in detail in.^18-21 The input and the output are shown in figure 4. The neurons work independently to the other nodes. The neurons gain information from the input layers which are processed and sent to the output layer. The connection between the neurons is stronger if the information is a priority and could be set with higher weights also known as the synaptic weights.

None.

Authors declare that there is no conflict of interest.

1. Kuz'michev VS, Tkachenko A, Krupenich IN, e al. Composing a virtual model of a gas turbine engine working process using the CAE system "ASTRA". Research Journal of Applied Sciences. 2014;9(10):635–643.
2. Bartolini CM, Caresana F, Comodi G, et al. Application of artificial neural networks to micro gas turbines. Energy Convers Manag. 2011;52(1):781–788.
3. Chipperfield A, Fleming P. Multi objective gas turbine engine controller design using genetic algorithms. IEEE Transactions on Industrial Electronics. 1996;43(5):583–587.
4. Bazazzadeh M, Badihi H, Shahriari A. Gas Turbine Engine Control Design Using Fuzzy Logic and Neural Networks. International Journal of Aerospace Engineering. 2011;2011:156796.
5. Ogaji SOT, Marinai L, Sampath S, et al. Gas-turbine fault diagnostics: a fuzzy-logic approach. Applied Energy. 2005;82(1):81-89.
6. Moinian F, Sabouhi H, Hushmand J, et al. Gas turbine preventive maintenance optimization using genetic algorithm. Int J Syst Assur Eng Manag. 2017;8:594–601.
7. Montazeri-Gh, Yousefpour H, Jafari S. Fuzzy logic computing for design of gas turbine engine fuel control system. The 2nd International Conference on Computer and Automation Engineering (ICCAE): Singapore; 2010. 723–727 p.
8. Thomas Jayachandran AV, Gangisetty G, Grigorev DI, et al. High Altitude Micro gas turbine power plant investigation of Parametric Analysis using Quantum Chemistry techniques for Alternate fuel optimization. ICRAFT; 2018.
9. Vimalachandran A, Tkachenko AY, Rybakov VN. Parametric Performance of Ultra-light Gas Turbine Power Plant for Heavy Lift Multicopters Flight Systems Using Astra-Russian Aviation Engine Optimization Software. MATEC Web Conf. 2018;220:03011.
10. Odom FM, Muster GL. Tutorial on Modeling of Gas Turbine Driven Centrifugal Compressors. Pipeline Simulation Interest Group; 2009.
11. Krivcov AV, Shabliy LS, Baturin OV. Gas-Dynamic Modeling of Gas Turbine Engine Components Collaborative Workflow. The Open Mechanical Engineering Journal. 2014;8:445–449.
12. Guolian H, Linjuan G, Zhile Y, et al. Multi-objective economic model predictive control for gas turbine system based on quantum simultaneous whale optimization algorithm. Energy Conversion and Management. 2020;207:112498.
13. Wei Y, Zhang X, Shi Y, et al. A review of data-driven approaches for prediction and classification of building energy consumption. Renewable and Sustainable Energy Reviews. 2017;82(1):1027–1047.
14. Richa C, Maity A, Paluri N. Modeling, Simulation and Validation of Mini SR-30 Gas Turbine Engine. IFAC-Papers OnLine. 2018;51(1):554–559.
15. Ellysia J, Nuratiah Z, Ali NA, et al. Machine learning versus linear regression modelling approach for accurate ozone concentrations prediction. Engineering Applications of Computational Fluid Mechanics. 2020;14(1):713–725.
16. Katayoun K, Saeed S, Javad P, et al. Estimating longitudinal dispersion coefficient in natural streams using empirical models and machine learning algorithms. Engineering Applications of Computational Fluid Mechanics. 2020;14(1):311–322.
17. Taghi Sattari M, Falsafian K, Irvem A, et al. Potential of kernel and tree-based machine-learning models for estimating missing data of rainfall. Engineering Applications of Computational Fluid Mechanics. 2020;14(1):1078–1094.
18. Romessis C, Mathioudakis K. Bayesian Network Approach for Gas Path Fault Diagnosis. Journal of Engineering for Gas Turbines and Power. 2006;128(1):64–72.
19. Bartolini CM, Caresana F, Comodi G, et al. Application of artificial neural networks to micro gas turbines. Energy Convers Manag. 2011;52(1):781–788.
20. Sisworahardjo NS, El-Sharkh MY, Alam MS. Neural network controller for microturbine power plants. Electric Power Syst Res. 2008;78(8):1378–1384.
21. Fast M, Assadi M, De S. Development and multi-utility of an ANN model for anindustrial gas turbine. Appl Energy. 2009;86(1):9–17.