NEO (Near Earth Objects) are near-Earth space objects (asteroids and comets), whose orbit approaches the planet at one third of the average Earth-Sun distance. NEO are potentially capable of hitting Earth in the next century, with the exception of comets that can do so by the gravitational effect of Jupiter, pushing them into the Solar System. Current estimates¹ indicate about 940 near-Earth objects larger than 1 kilometer in diameter. The US Congress has set targets for NASA's search for NEO, with 90% of them with a diameter of up to 1 km or greater in 10 years. This was motivated by a recent discovery in 2009 of a NEO approximately 2 to 3 km in diameter. These objects could cause global devastation if they hit Earth. In this research the NEO-Earth collision dynamics is studied and a statistic of physical and technological parameters is established as a mitigation strategy.

Keywords: NEO, collision, mitigation, technological parameters

The Solar System is populated by various cosmic objects that orbit its planets and others that penetrate it, attracted by its gravity. The objects collide with the planets, escape from it with greater or lesser energy, or are captured by its gravity and orbit the planets. An example of a collision was Comet Shoemaker-Levy 9 which broke up and collided with Jupiter. Calculations showed that the comet passed Jupiter's Roche boundary in July 1992, and tidal forces from the planet caused it to break up into many pieces up to 2 km in diameter and with impact speeds reaching 60 km/s.² Planet Earth is continually bombarded by cosmic objects. Most of them are small in size and quickly glow due to friction with gases in the atmosphere. However, others survive this process and, depending on the resulting size, can cause irreparable and permanent damage to life on Earth. Space debris is an example of these objects and asteroids that are close to the planet (NEO) as well. Scientists cannot predict the timing and location of future impacts, but they can compile statistics and propose strategies to prevent destructive collisions of large objects with Earth. The most accurate statistical impact projections say that objects larger than about 30 meters in diameter hit the planet only about once in a few centuries, while objects with a diameter ten times larger only once in a few millennia. But even those with a diameter of the order of 30 meters can cause immense damage. Furthermore, impacts on Earth by very close objects are unavoidable. The best-known case in recent history happened on June 30, 1908, of an object in Tunguska in Siberia that devastated more than 2,000 square kilometers of forest. Recent research indicates that it would have been 30 to 50 meters in diameter, and much of the damage it caused was due to shock waves from the object's explosion in Earth's atmosphere (air-burst).^3–5 According to O’Keefe and Ahrens,⁶  the evidence of the largest impact that the Earth has suffered was in the Yucatan Peninsula, Mexico, which resulted in the Chicxulub crater, approximately 200 kilometers in diameter. The impact is believed to have taken place 65 million years ago and to have wreaked global devastation, wiping out plants and groups of animals, including dinosaurs in large numbers. Our work aims to study the possibility of a collision of a NEO with the planet Earth, implementing mitigation maneuvers through kinetic impact, in order to divert the NEO from its collision course with the planet. These objects are at 1/3 AU and have the potential to hit Earth in the next century. Statistical projections indicate that in the coming centuries or millennia the frequency of impacts with larger and larger objects will increase. Forecasts show collisions with objects with diameters on the order of kilometers for the middle and far future, which would be fatal for Earth. It is a rare phenomenon, but if it occurs it will be destructive and global. But, the size of an object that would cause significant devastation on the planet is still uncertain.⁷ In addition, NEOs measuring around 140 m have the potential to cause tsunamis if they fall into the ocean. The average amount of material accumulated daily on Earth is estimated to be in the range of 50 to 150 tons of very small objects.⁸ This material is mostly dust, although there are small objects that burn quickly in the atmosphere and are evidenced by meteor trails. There are more than 170 impact craters established on Earth, including the approximately 1.2 km Meteor Crater in Arizona. The largest known terrestrial crater is the 300 km diameter Vredefort Crater in South Africa. A stony meteorite 1 to 2 meters in diameter traveling at high supersonic speeds created an impact crater in Peru in September 2007. Normally, such a small object should not have impacted the surface at such a high speed. This case demonstrates that specific situations can vary greatly from the expected norm and is a reminder that small near-Earth objects can also be dangerous. On October 6, 2008, asteroid 2008 TC3 was observed by the Catalina Sky Survey (near-Earth object detection program) on a collision course with Earth. The 2-5 meter diameter object entered the atmosphere on 7 October 2008 and the resulting fireball was observed in northern Sudan.⁹ Subsequent surveys in the Nubian Desert of Sudan located 3.9 kilograms (in 280 fragments) of meteorite material. Current estimates indicate that there must be a total of approximately 940 near-Earth objects larger than 1 km in diameter.¹ This includes near-Earth asteroids, but does not include long-period comets (orbital periods greater than 200 years), which are believed to have less than on the order of 1% of the total impact threat.¹⁰ According to Toon et al.,¹¹ asteroid impacts between 2 to 3 km in diameter may be capable of causing global damage due to the storm generated by falling debris, which may affect the climate and produce the so-called asteroid winter. Although impacts from objects smaller than 1 km in diameter cause less damage than larger ones, it is this class of smaller objects that, because of their much greater numbers, present the most frequent threat to humanity. The reports by Stokes et al.,¹⁰ and NASA PA&E¹² analyzed available data on near-Earth objects and made extensive calculations of the potential danger to humanity from various populations of these objects. The method is quite detailed in dynamic modeling to determine the primary source regions of near-Earth objects. These surveys find that about 20% of these objects have orbits that pass within 0.05 AU of Earth. According to estimates by Hills and Goda,¹³ hard stone objects, between 40 and 150 meters in diameter, explode when they enter the Earth's atmosphere and generate air explosions capable of producing superficial damage. In this way, they are similar to the explosion at Tunguska. The results of the research by Stokes et al.,¹⁰ indicate that 75% of all impacts do not produce any deaths because they fall into oceans or uninhabited land areas. However, when impacting the oceans, asteroids or comets can affect their immediate surroundings, and have the potential to launch tsunamis that flood coasts and affect populated areas. Smaller impacts could be misinterpreted and thus trigger wars. Given the inevitability of impacts, research has been carried out with the purpose of creating appropriate actions to mitigate objects close to the planet with the possibility of collision. For larger events, changing the dangerous object's orbit is probably ideal. But the choice of how best to do this depends both on the mass of the object that has to be moved and on the level of danger that object represents, and on the details of the orbit. Board et al.,⁷ present four current mitigation categories: civil defense, slow push or pull methods, kinetic impact and nuclear detonation. The kinetic impact strategy was demonstrated (Deep Impact mission that designed an impact spacecraft to collide with Comet Tempel-1 in July 2006). The other options did not advance beyond the conceptual phase. Even with the Deep Impact mission, which produced a 10 km/s impact on a 6-km-diameter body, the operation was by far on a much smaller scale than would be required for ground defense against a 100-meter-diameter NEO.  In addition, it impacted a relatively large object and therefore easier to hit. Thus, it appears that research in this area is still new and immature, from a scientific point of view. In this work, we will focus attention on kinetic impact methods, considering the effectiveness of the spacecraft's propulsion system that will impact with the NEO. Through a strategy based on the control of variables of the relative collision dynamics between objects, we intend to establish mitigation conditions for such hazards.

The methodology used in this work seeks to simulate the equations of the relative dynamics between the space object that orbits on a collision course with the planet Earth and a propelled space vehicle that will be projected towards it with the objective of causing a deflection in its orbit. This collision between the space objects (NEO and vehicle) will produce a final trajectory of the NEO that moves away from the collision condition with Earth. This maneuver is called a kinetic impact maneuver. In Figure 1, we show three bodies (Earth, NEO and space vehicle) involved in this dynamics and two reference systems, one centered on Earth and the other centered on the space vehicle.

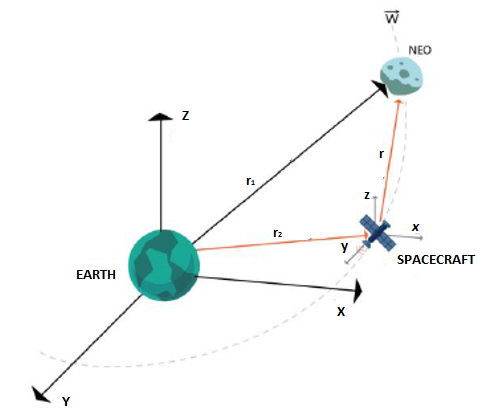
Figure 1 Earth-centered reference systems (x,y,z) and center reference system on the space vehicle (x,y,z).

The NEO's orbit will at some point cross the Earth's orbit and there will be a collision between them, which could be catastrophic for the planet, depending on its mass. Our strategy is to send a space vehicle to intercept the NEO and prevent the collision with Earth from happening. The kinetic impact must happen when the relative position between the space vehicle and the NEO is zero, that is, when r ⃗=0 ⃗. This condition must be achieved by propulsion of the vehicle, which will launch it over the NEO in a well-defined direction and with sufficient speed to create an angular deflection in relation to planet Earth. This deflection should be enough to keep out from colliding with the planet. This is the mitigation scenario. In it, the target's orbit (NEO) would be altered with an impact of a vehicle with a very high speed payload. The effectiveness of this option depends not only on the mass of the target, but also on the net result of the operation, which can project material off the target (object fragmentation) in the opposite direction of the payload after impact. This method is relatively simple and effective for objects with diameters of up to about half a kilometer when there are years or more of warning time. Figure 2 shows the reference system centered on the space vehicle, with the x direction pointing away from Earth and perpendicular to the vehicle's orbit, the y direction is in the direction of the vehicle's flight in the orbital plane, and the z direction is normal to the space vehicle's orbit. In this dynamics, we consider the Earth gravitationally interacting with the NEO and with the space vehicle and the propulsion force acting on the vehicle.

Figure 2 Reference systems – centered in space vehicle.

That is, the vehicle's trajectory, C, is on a plane that is perpendicular to the X-axis, which points away from Earth. The flight direction is the Y-axis direction and the Z-axis is perpendicular to the plane of the vehicle's orbit. Angle f is outside the XY plane and angle theta q is the angle that the projection of the relative vehicle-NEO position makes with the X-axis onto the XY plane. The vehicle follows a circular path around the Earth with constant angular velocity $\overrightarrow{w}=\overrightarrow{cte}=w\widehat{z}$ . The relative position between the two objects (vehicle and asteroid-NEO) is,$\overrightarrow{r}$ measured from the center of the vehicle, where the XYZ reference system is fixed.  The relative distance between the two objects (vehicle and asteroid-NEO) is r, measured from the center of the vehicle, where the XYZ reference system is fixed. The kinetic impact will occur when $\overrightarrow{r}|=r=0$  or when the gravitational effects between the bodies are strong enough to cause the desired NEO trajectory deflection.

The dynamics of the terrestrial space environment, composed by these objects, consists of the N-body gravitational problem. REBOUND is an API (Application Programming Interface) that enables numerical simulation with a high degree of precision for this dynamic [Rein and Liu 2012, Rein and Spiegel 2014, Rein and Tamayo 2015]. IAS15 was chosen as an integrator, with adaptive pitch, as it achieves machine precision in integrations of billions of orbits and in dynamics of close encounters between objects and, therefore, the most suitable for this model. In REBOUND, all bodies in the simulated system are treated as point particles. The simulated system for this study is composed of Earth, NEO and a space vehicle. The gravitational acceleration that a particle i undergoes due to the N-particles is given by:

${\overrightarrow{a}}_i={\displaystyle \sum _{j=1;j\ne i}^N\frac{G{m}_j}{{\left(r_{ij}{}^2-d^2\right)}^{\frac{3}{2}}}}{\overrightarrow{r}}_{ij}$   (1)

where G is the gravitational constant $\left(6.67 x {10}^{-11}{m}^{3}k{g}^{-1}{s}^{-2}\right)$ ,$M_j$ is the mass of particle $j$ and $r_{ij}$ is the relative distance between particles j and i. The parameter d is the average radius of the particles of the system, being necessary to avoid singularities in the gravitational acceleration in the collision events between the particles. The N particles can be gravitationally active or non-active. Active particles are said to be massive, that is, particles that gravitationally interact with particle i.

The model for the vehicle propellant mass in this dynamic is exponential decay, that is,

$M\left(t\right)= m_o\left(\chi +e^{-\gamma t}\right)$   (2)

where the magnitudes “power factor”, γ>0, is the propellant ejection frequency in time and “mass factor”, χ>1, is the ratio between the vehicle mass $M_o$ and the initial propellant $(m_o)$ mass, according to Jesus.¹⁴ Furthermore, the propulsion force per unit mass is given by:

$\overrightarrow{f}=-\overrightarrow{v_e}\frac{d\left[M\left(t\right)\right]}{dt}$   (3)

where $\overrightarrow{v_e}$ gas exhaust velocity and, together with the parameters γ and χ, are called technological parameters. In this way, knowing these technological parameters and the initial conditions, it will be possible to control the collision conditions of the vehicle with the NEO. But, we still need information on the direction of the kinetic impact velocity. In this case, we display the exhaust velocity Cartesian components as a function of steering angles, such that (using the spacecraft centered reference system with α=π/2-θ and β=ϕ),

$v_{ex}\left(t\right)= V_{o}cos\alpha \left(t\right).sen\beta \left(t\right)$   (4)

$v_{ey}\left(t\right)= V_{o}sen\alpha \left(t\right).sen\beta \left(t\right)$   (5)

$v_{ez}\left(t\right)= V_{o}cos\beta \left(t\right)$   (6)

These Equations are written in the spacecraft centered system (Figure 2). The question to be answered is: what is the strategy for mitigating the collision of the NEO with Earth? The answer lies in studying the efficiency of the propulsion system's shot in deflecting or deflecting the NEO's orbit that is on a collision course with Earth. The shooting direction angles are and can be “controlled” together with the technological parameters that define the proximity of the collision objects, in order to avoid the collision with the planet. In this way, the result of this study will be the establishment of a statistic that will show the ranges of values for such technological parameters and also the validity intervals of the angles that allow the success of the strategy.

The physical magnitudes of the gravitational interaction and technology that define the propulsion of the colliding space vehicle (probe, missile, etc.) combine in the relative collision dynamics between the space vehicle and the NEO approaching Earth on a collision course. Our simulations made it possible to perform statistics on the distribution of values of these quantities that materialized a deflection in the NEO's orbit and, as a consequence, a distance from it with respect to our planet, thus avoiding a collision. Initially we use the Solar System example that integrates all the planets of the solar system. We adapted the code so that we had the interaction of only 3 particles behaving like Earth, Spacecraft (kinetic impact) and NEO. With this we simulate the dynamics in the REBOUND environment, which considers the gravitational interactions and propulsion force and the collision condition of the vehicle with the NEO, to implement the deflection. The mitigation strategy used in this work was the following: 1) initially, we found the physical conditions of collision of the NEO with the Earth. In reality it is a physical collision, where, under the gravitational effect of the associated three-body problem (Earth, NEO and vehicle), we make the relative distance between NEO and Earth cancel out. These conditions include the true anomaly of the NEO (its angular position measured in relation to the focus where the Earth is located, other Keplerian elements of the orbit and the minimum distance to Earth provided by the NASA catalog at https://cneos.jpl.nasa. gov/ca/); 2) in possession of the physical conditions favorable to the collision, we activated the thrusters to provoke a technological collision (maneuver controlled by the propulsion) of the vehicle with the NEO, in order to cause a deflection in it, such that its final distance D, in relation to Earth be maximized. The NEO's initial distance from Earth is 747,263 km. NEO is detected in a certain position characterized by the Keplerian elements that determine its orbit in time. This initial value of D is determined by the distance between the line passing through the Earth's center of mass and the trajectory of the NEO. The value of 747.263 km represents certain and imminent collision with the planet. Figure 3 shows the position of the NEO in relation to the Earth for various values of the true anomaly. This relationship is important, because it allows us to choose the appropriate anomaly for a collision time that must be compatible with the simulation time of the maneuver.

Figure 3 NEO-earth vs. time.

The graph shows that as the true anomaly magnitude increases, the time to collision also increases. This result indicated that we should choose a small anomaly so that the collision occurs faster, given the simulation time demand. The anomaly chosen for the simulations was -179.7824145334923401 degrees. The graphs in Figures 4–8 present the results of the simulations of the mitigation maneuvers, considering the burning of propellers only in the X direction (Eq. (4) – (6)). Initially, we looked for the best out-of-plane angle (Beta) that allows the greatest separation D of the NEO in relation to Earth, after its collision with the intercepting vehicle (collider). The mass of NEO was assumed to be 8.2E7 (kg). In Figure 4 the α angle is fixed at 10 degrees, the γ power factor 1E-6 and mass factor e χ= 10, initial speed $v_o$ = 1 km/s.

Figure 4 Angle outside the orbit plane vs. NEO's final distance from earth.

This graph was constructed for an angle in the fixed plane, α = 10 degrees, and indicates that there is an angular region for the angle outside the orbit plane β that is favorable for the NEO approach to Earth and another that is unfavorable. The best angle was around 165 degrees which gives the greatest separation D. With this angle fixed, we look for the optimal angle in the orbit plane, that is, the α angle. Figure 5 shows the results. For this simulation we set the out-of-plane angle at β=165 degrees. The other factors remain with their constant values.

Figure 5 Angle in the orbit plane vs. NEO's final distance from earth.

In this case, we found that the optimal angle was 180 degrees. With this pair of optimal angles, we can test the best value of the thruster initial velocity module to achieve the final greatest distance between the NEO and the Earth. Figure 6 shows the result.

Figure 6 Thrust Initial Velocity vs. NEO's final distance from Earth (β = 165°, α = 180°).

This graph shows that the best value of the thrust initial velocity module that gives the greatest distance between the NEO and the Earth is 2 km/s. With these optimal parameters, we will find the other technological characteristics such as the mass and power factors. Figure 7 shows how the final distance behaves with the motor power factor.

Figure 7 Power Factor vs. NEO's final distance from Earth.

This graph shows a peak in the final distance from the NEO to Earth for a power factor of ${10}^{-7}(1/s)$ . From this value there is a drop in the final distance. The propulsion force is proportional to this factor and if it is very small, its magnitude becomes very small and that is what we see in the behavior of the curve. That is, for small values of the power factor, it will not be possible to cause significant deflection in the NEO to increase its final distance from Earth. Figure 8, shows the effect of the mass factor on the mitigation maneuver.

Figure 8 Mass Factor vs NEO's final distance from Earth.

We clearly see that the final distance of NEO from Earth decreases with increasing mass factor. That is, smaller mass factors are more desirable to achieve a more efficient mitigation maneuver. This means that smaller vehicles are desirable for this operation or vehicles with a large (initial mass) load. Smaller vehicles may be more efficient, injecting an impact at a point that better deflects the NEO, than larger vehicles hitting a larger region of the NEO. The best value found for this factor was 2. It is important to say that this result is partial, as it is a shot in the X direction. Thus, the maximum distance of NEO's departure from the Earth, when a shot for exclusive firing directions in the Y and Z directions. In Table 1, we show the results of these simulations for the distances in relation to the α and β angles, and in relation to the technological parameters. The complete thrust refers to the firing of thrusters in all directions at the same time, with no preferred direction.

In this work we performed simulations of mitigation maneuvers to produce deflection of a NEO approaching Earth on collision course. The results showed that physical and technological conditions allow successful mitigation to be carried out. We verified that there are ranges of angles in the plane, α, and out of the orbit plane, β, that are favorable to the collision and others that are unfavorable. The results showed that the best deflection that provides the greatest final distance of the NEO in relation to the Earth, occurs for a mitigation strategy aiming the exhaust velocity exclusively in the X direction, thus avoiding the collision with our planet. A statistic of the physical and technological magnitudes has been established and, from there, the mitigation maneuvers can be carried out.

None.

The author declares that there is no conflict of interest.

1. Harris AW. The NEO population, impact risk, progress of current surveys, and prospects for future surveys. Presentation to the Survey/Detection Panel of the NRC Committee to Review Near-Earth Object Surveys and Hazard Mitigation Strategies. Space Science Institute; 2009.
2. Solem JC. Density and size of comet Shoemaker-Levy 9 deduced from a tidal breakup model. Nature. 1994;370:349–351.
3. Chyba CF, PJ Thomas, KJ Zahnle. The 1908 Tunguska explosion Atmospheric disruption of a stony asteroid. Nature. 1993;361:40–44.
4. Boslough MBE, Crawford DA. Shoemaker-Levy 9 and plume-forming collisions on Earth. Annals of the New York Academy of Sciences. 1997;822:236–282.
5. Boslough M, Crawford D. Low-altitude airbursts and the impact threat. International Journal of Impact Engineering. 2008;35:1441–1448.
6. O’Keefe JD, TJ Ahrens. Impact production of CO2 by the Cretaceous/Tertiary extinction bolide and the resultant heating of the Earth. Nature. 1989;338:247–249.
7. Board. Defending planet earth: Near-Earth-Object surveys and hazard mitigation strategies. National Academies Press; 2010.
8. Love SG, Brownlee DE. A direct measurement of the terrestrial mass accretion rate of cosmic dust. Science. 1993;262:550–553.
9. Jenniskens P. The impact and recovery of asteroid 2008 TC3. Nature. 2009;458:485–488.
10. Stokes G, Yeomans D, Bottke WF, et al. A Study to Determine the Feasibility of Extending the Search for Near Earth Objects to Smaller Limiting Magnitudes. Report Prepared at the Request of NASA Headquarters Office of Space Science’s Solar System Exploration Division. 2003.
11. Toon OB, Zahnle K, Morrison D, et al. Environmental perturbations caused by the impacts of asteroids and comets. Reviews of Geophysics. 1997;35:41–78.
12. Near-Earth Object Survey and Deflection Study. NASA PA&E (NASA Program Analysis and Evaluation). NASA Headquarters, Washington, DC; 2006.
13. Hills JG, Goda MP. The fragmentation of small asteroids in the atmosphere. Astronomical Journal. 1993;105:1114–1144.
14. Jesus ADC. Evasive Maneuvers in Space Debris Environment and Technological Parameters. Mathematical Problems in Engineering. 2012;15:2012.