The attitude control of an asteroid-orbiting spacecraft based on immersion and invariance (I&I) theory is the subject of this paper. It is assumed that the moment of inertia matrix and the gravitational parameters are not known. The objective is to attain nadir pointing attitude on an elliptic orbit. First, based on the I&I principle, an adaptive attitude control system using the Modified Rodrigues Parameters (MRPs) is derived. Through the Lyapunov stability analysis, the asymptotic convergence of the MRP trajectories to the origin is established. Interestingly, in contrast to traditional adaptive systems, the trajectories of the closed-loop system converge to an attractive manifold in an extended state space. Then, for the purpose of comparison, this MRPs-based control law and a quaternions-based control system (also designed using the I&I principle) are simulated for the attitude control of the spacecraft in eccentric orbits around asteroid 433 Eros. It is observed that while each I&I-based control law can accomplish precise attitude control, for identical design parameters in these two control systems, the MRPs-based control law requires smaller control magnitude and accomplishes smoother convergence of trajectories to the attractive manifold, but requires larger settling time for the attitude trajectories, compared with the quaternions-based adaptive control law.

Keywords: asteroid-orbiting spacecraft, adaptive attitude control, immersion and invariance, parameter identifier, gravitational potential, nonlinear system

For scientific exploration, missions to small bodies in the solar system, such as asteroids and comets, are extremely important. There have been several successful missions, such as NEAR, Hayabusa I, and Rosetta, and future missions (DART, Lucy, and Psyche) have been planned. Transporting near-Earth asteroids to halo orbits in the Earth-Moon system is of special interest to NASA. Additionally, transmitters can be stationed on asteroids for interplanetary flights.

Asteroids have irregular shapes and non-uniform density, and their gravitational force varies with the spatial coordinates of orbiting spacecraft. Researchers have analyzed the effect of the non-uniform gravity field of asteroids on attitude dynamics.^1-4 It has been found that certain combinations of orbital and asteroid rotational rates can cause pitch resonance.^1,2 Based on the Poincare section, the attitude motion of spacecraft has been analyzed.3 The authors have analyzed orbit-attitude coupled dynamics around small bodies and obtained a natural Sun-synchronous orbit and Sun-tracking attitude.⁴ For a linear time-varying model, an inverse control law for the yaw, pitch, and roll angle control has been designed.² A nonlinear attitude control law for spacecraft with a large captured object (asteroid) has been derived.⁵ Researchers have also designed control systems for position and attitude control of spacecraft operating in the vicinity of asteroids.^6-11 The design proposed by authors⁷ yields a finite time control law. Also, an adaptive sliding mode controller,⁸ a robust adaptive system,⁹ and a nonlinear control law based on the Lyapunov theory¹⁰ for orbit and attitude control have been derived. Based on a Hamiltonian representation of the coupled orbit-attitude dynamics, a control law has been obtained.¹¹

For the control of nonlinear uncertain systems, a design methodology based on the notion of immersion and invariance (I&I) has been developed by Astolfi and Ortega¹² and Astolfi et al.¹³ This design method yields a noncertainty-equivalence adaptive (NCEA) control system. Unlike traditional certainty-equivalence adaptive (CEA) schemes,¹⁴ the I&I-based designed identifier provides a net parameter estimate as a sum of a signal derived from an integral adaptation rule and an algebraic function. The identifier of NCEA systems provides stronger stability properties in a closed-loop system. The original design methodology, developed by the authors,^13,14 requires solution of a partial differential (matrix) inequality, which is not an easy task. Seo and Akella¹⁵ proposed use of the filtered signals to overcome this difficulty and designed a quaternion-based NCEA law for the attitude control of a rigid body. The solvability requirement of the partial differential inequality can also be avoided by using dynamic scaling.¹³ A dynamic scaling-based NCEA attitude control law has been developed.¹⁶ An NCEA law has been designed for the pose control of a 6-DOF Earth-orbiting spacecraft described by dual quaternion.¹⁷ Also, a filter-free NCEA attitude control system has been proposed, which yields faster responses, compared with a controller with filters.¹⁸ NCEA laws have also been considered for hovering and the orbit control in the vicinity of asteroids.^19,20 Recently, I&I-based adaptive control systems for the regulation of the yaw, pitch, and roll angles²¹ and quaternion trajectory²² of asteroid-orbiting spacecraft have been developed. A supertwisting control system for the control of spacecraft orbiting around asteroid has been developed.²³ In a recent paper, based on the immersion and invariance principle, a generalized composite adaptive control law for asteroid-orbiting spacecraft has been designed.²⁴

The attitude parameterization using a quaternion vector of dimension four is often made. However, for simplicity, the modified Rodrigues parameter (MRP) vector consisting of only three elements can be used for attitude representation. But the modified Rodrigues parameters (MRPs) are limited to eigen-axis rotations in the interval [0; 360) degrees. Of course, this limitation can be overcome by the use of shadow MRP.^25,26 The authors have proposed sliding mode, CEA, and passifying control systems for MRP attitude control.^27-29 It appears from the literature that an MRP-based NCEA attitude control law has not been designed for asteroid-orbiting spacecraft. Because NCEA laws provide parameter estimators with stronger stability properties, it is of interest to design an MRP-based attitude control system for asteroid related missions.

In this paper, the development of an adaptive attitude control law for nadir pointing of spacecraft - orbiting in elliptic orbits around rotating asteroids-is considered. This is important for the continuous observation of specific region of asteroid. It is assumed that the moment of inertia matrix of the spacecraft and asteroid's gravity field parameters are unknown.

The contribution of this paper is three-fold. First, an I&I-based NCEA attitude control law for the spacecraft model-including kinematics described by the MRPs-is designed. For the derivation of control law, a backstepping design method is adopted. Second, the asymptotic regulation of the MRP trajectory to the origin using Lyapunov stability analysis is established. Interestingly, unlike classical CEA systems, closed-loop system's trajectories converge to a manifold ℳ_a (to be defined later) in an extended-state space. Third, numerical results are presented for the MRP trajectory regulation of a spacecraft orbiting in eccentric orbits around asteroid 433 Eros. The results show precise attitude control despite uncertainties in the model. Also, for the purpose of comparison, the closed-loop system including the I&I-based adaptive law22-designed for quaternion trajectory control-is simulated. The results show that for identical feedback gains in the two control systems, the MRP-based control law requires a smaller control magnitude and achieves smoother convergence of trajectories to the manifold ℳ_a compared with the quaternion-based controller, but the settling time for the attitude trajectories is larger.

The spacecraft orbiting in an equatorial orbit - around an irregularly-shaped asteroid-is shown in Figure 1. In the figure, (X_I, Y_I, Z_I), (X₀, Y₀, Z₀), and (X_B, Y_B, Z_B) represent an inertial frame (with its origin at the center of mass of the asteroid), an orbital frame, and a body-fixed frame (both centered at the center of the mass of the satellite), respectively. The asteroid is rotating about Z_I normal to the equatorial plane with a constant rate Ω. Another frame , fixed to the asteroid (not shown in the figure), is aligned with the three centroidal principal axes of the asteroid. The axis X₀ is in the orbital plane and points in the transverse direction; Z₀ is along the radial line pointing towards the asteroid's center of mass; and Y₀ = Z₀ X₀ is normal to the orbit plane. For equatorial orbits, (X₀, Y₀, Z₀) frame is obtained from (X_I, Y_I, Z_I) by a single rotation angle equal to the true anomaly η.

Figure 1 Asteroid-orbiting spacecraft.

For this study, the dynamical model of the spacecraft, developed by Reyhanoglu et al.¹⁰, is considered, but their model uses a four dimensional quaternion vector q_a to represent the kinematic equations. In this paper, it is of interest to describe the attitude, using the MRP vector $\sigma \in R^3$ for simplicity. Therefore, certain modifications in the spacecraft dynamical model¹⁰ will be necessary. Now, the attitude of the spacecraft with respect to the orbital frame is described by the MRP vector $\sigma ={\left[{\sigma }_1,{\sigma }_2,{\sigma }_3\right]}^T\in R^3$ , which satisfies:

$\sigma =\tan \left(\frac{\Phi }{4}\right)\widehat{e}$   (1)

where $\widehat{e}$ and Φ are Euler's principal rotation axis and principal angle of rotation, respectively. Thus, Eq. (1) has singularity at Φ= ±360 [deg]. However, this limitation can be removed by switching σ to the shadow MRP ${\sigma }^S=-\sigma {\left({\sigma }^T\sigma \right)}^{-1}$ , when $\Vert \sigma \Vert \ge 1$ .^25,26 The direction cosine matrix $C^{bo}\left(\sigma \right)$ from the orbital frame to the frame (X_B, Y_B, Z_B) can be written in a compact form as:²⁶

$C^{bo}\left(\sigma \right)=I_{3\times 3}+\frac{\left[8S^2\left(\sigma \right)-4\left(1-{\Vert \sigma \Vert }^2\right)S\left(\sigma \right)\right]}{{\left(1+{\Vert \sigma \Vert }^2\right)}^2}$   (2)

where $\Vert \sigma \Vert ={\left({\sigma }^T\sigma \right)}^{\left(1/2\right)}$ , and for any vector $\xi =\left[{\xi }_1,{\xi }_2,{\xi }_3\right]T,S\left(\xi \right)$ is the skew-symmetric matrix defined as:

$S\left(\xi \right)=\left[\begin{array}{ccc}0& -{\xi }_3& {\xi }_2\\ {\xi }_3& 0& -{\xi }_1\\ -{\xi }_2& {\xi }_1& 0\end{array}\right]$

The angular velocity of the orbital frame with respect to the inertial frame expressed in the orbital frame is ${\omega }_o={\left[0,-\dot{\eta },0\right]}^T$ , where η is the true anomaly. Let the angular velocity of the spacecraft with respect to the inertial frame (expressed in the body frame (X_B, Y_B, Z_B)) be $\omega \in R^3$ . Also, denote the relative angular velocity of the spacecraft with respect to the orbital frame as ${\omega }_{bo}\in R^3$ . Then ${\omega }_{bo}$ can be written as:

${\omega }_{bo}=\omega -C^{bo}\left(\sigma \right){\omega }_o=\omega +\dot{\eta }{c}_2^{bo}\left(\sigma \right)$   (3)

where $C^{bo}\left(\sigma \right)=\left[c_1^{bo},c_2^{bo},c_3^{bo}\right]$ and $c_i^{bo}\left(\sigma \right)\in R^3$ is the ith column of $C^{bo}$ . (Often the arguments of functions and matrices are suppressed for simplicity.)

The MRP vector σ satisfies the following differential equation:²⁶

$\dot{\sigma }=\frac{1}{4}B\left(\sigma \right){\omega }_{bo}$   (4)

Where:

$B\left(\sigma \right)=\left[\left(1-{\Vert \sigma \Vert }^2\right)I_{3\times 3}+2S\left(\sigma \right)+2\sigma {\sigma }^T\right]$   (5)

The rotational equations of motion of the spacecraft are:

$J\dot{\omega }=-S\left(\omega \right)J\omega +M_g\left(\sigma \right)+u+d$   (6)

where u = [u₁, u₂, u₃]^T, J = diag{J₁, J₂, J₃}, M_g = [M_g1, M_g2, M_g3]^T, and $d\in R^3$ are the control torque vector, principal inertia matrix, gravity gradient torque vector, and disturbance input, respectively.

For the computation of M_g, the following functions are introduced:¹⁰

$\varphi =\left[-1.5C_{20}+9C_{22}\cos \left(2{\lambda }_c\right)\right]{\left(r_0/R_c\right)}^2$

$\chi =6C_{22}\sin \left(2{\lambda }_c\right){\left(r_0/R_c\right)}^2$   (7)

where λ_c is longitude of the center of mass of the satellite, R_c is the radial distance between the centers of mass of the asteroid and the spacecraft, and r₀ is the characteristic length. Here, only the most significant spherical harmonic coefficients C₂₀ and C₂₂ of the gravitational potential are considered.¹⁰ (Of course, the design method is applicable, if additional coefficients are used.) The gravitational parameter of the asteroid is μ = GM_a, where G is the universal gravitational constant, and M_a is the mass of the asteroid. Here, the satellite's orbit in the equatorial plane is considered. For prograde orbits, one has ${\lambda }_c\left(\eta ,t\right)=\left(\eta -\Omega t\right)$ , where is the asteroid's constant angular rate.

The gravity torque M_gi, (i = 1, 2, 3), derived by Reyhanoglu et al.¹⁰, are considered for design, but now, the MRP-dependent matrix $C^{bo}\left(\sigma \right)$ is used for computation. Thus, M_gi(σ); (i = 1, 2, 3) are given by:

$M_{g1}\left(\sigma \right)=\frac{\mu }{R_c^3}\left[\left(3+5\varphi \right)\left(J_3-J_2\right)c_{23}^{bo}{c}_{33}^{bo}+2.5\chi \left\{-0.4J_1{c}_{12}^{bo}-\left(J_1+J_2-J_3\right)c_{21}^{bo}{c}_{33}^{bo}+\left(J_1-J_2+J_3\right)c_{23}^{bo}{c}_{31}^{bo}\right\}\right]\doteq {\psi }_{a1}\left(\sigma \right)p$   (8)

$M_{g2}\left(\sigma \right)=\frac{\mu }{R_c^3}\left[\left(3+5\varphi \right)\left(J_1-J_3\right)c_{13}^{bo}{c}_{33}^{bo}+2.5\chi \left\{-0.4J_2{c}_{22}^{bo}+\left(J_1+J_2-J_3\right)c_{11}^{bo}{c}_{33}^{bo}-\left(J_2+J_3-J_1\right)c_{13}^{bo}{c}_{31}^{bo}\right\}\right]\doteq {\psi }_{b1}\left(\sigma \right)p$   (9)

$M_{g3}\left(\sigma \right)=\frac{\mu }{R_c^3}\left[\left(3+5\varphi \right)\left(J_2-J_1\right)c_{13}^{bo}{c}_{23}^{bo}+2.5\chi \left\{-0.4J_3{c}_{32}^{bo}+\left(J_2+J_3-J_1\right)c_{13}^{bo}{c}_{21}^{bo}-\left(J_1-J_2+J_3\right)c_{11}^{bo}{c}_{23}^{bo}\right\}\right]\doteq {\psi }_{c1}\left(\sigma \right)p$   (10)

where $c_{ij}^{bo}\left(\sigma \right)$ is the ijth element of matrix $C^{bo}\left(\sigma \right)$ , and:

$p={\left[J_1,J_2,J_3,C_{20}{J}_1,C_{20}{J}_2,C_{20}{J}_3,C_{22}{J}_1,C_{22}{J}_2,C_{22}{J}_3\right]}^T\in R^3$

is assumed to be an unknown parameter vector. Define a regressor matrix ${\psi }_1\left(\sigma \right)={\left[{\psi }_{a1}^T,{\psi }_{b1}^T,{\psi }_{c1}^T\right]}^T\in R^{3\times 9}$ . Then, the gravity torque takes a compact form as:

$M_g\left(\sigma \right)={\psi }_1\left(\sigma \right)p$   (11)

Substituting Eq. (11) in (6) and assuming that disturbance input d is zero, one obtains:

$J\dot{\omega }=-S\left(\omega \right)J\omega +{\psi }_1\left(\sigma \right)p+u$   (12)

The objective is to design a control law for the system (4) and (12) such that ${\left({\sigma }^T,{\omega }_{bo}^T\right)}^T$ asymptotically converges to zero, despite uncertainties in the parameter vector p. Then, it follows that the spacecraft will attain a nadir pointing attitude.

The design is based on a backstepping method. For the design, it is assumed that the disturbance torque d(t) is zero. (Later, robustness of control law will be examined by simulation for d ≠ 0).

Step 1

With an objective to regulate σ to zero, consider a Lyapunov function:

$W_1\left(\sigma \right)=2\ln \left[1+{\sigma }^T\sigma \right]$   (13)

Its derivative along the solution of Eq. (4) is:

${\dot{W}}_1=4\left[\frac{1}{1+{\sigma }^T\sigma }\right]{\sigma }^T\left[\frac{1}{4}\right]B\left(\sigma \right){\omega }_{bo}$   (14)

Using B from Eq. (5), one can verify that:

${\sigma }^{T}B\left(\sigma \right)=\left(1+{\Vert \sigma \Vert }^2\right){\sigma }^T$   (15)

Let ${\omega }_v$ be a virtual stabilizing signal, and define the error ${\omega }_e={\omega }_{bo}-{\omega }_v$ . Then, using Eq. (15), Eq. (14) gives:

${\dot{W}}_1={\sigma }^T\left[{\omega }_e+{\omega }_v\right]$   (16)

Selecting ${\omega }_v$ as:

${\omega }_v=-k_1\sigma ,k_1>0$   (17)

and then, substituting Eq. (17) in Eq. (16) gives

${\dot{W}}_1=-k_1{\Vert \sigma \Vert }^2+{\sigma }^T{\omega }_e$   (18)

Step 2

Now, it is essential to regulate the error

${\omega }_e={\omega }_{bo}-{\omega }_v=\omega +\dot{\eta }{c}_2^{bo}\left(\sigma \right)+k_1\sigma$   (19)

to zero. Noting that ${\dot{C}}^{bo}\left(\sigma \right)=-S\left({\omega }_{bo}\right)C^{bo}\left(\sigma \right)$ , the derivative of $c_2^{bo}$ can be written as:

${\dot{c}}_2^{bo}\left(\sigma \right)=-S\left({\omega }_{bo}\right)c_2^{bo}\left(\sigma \right)$   (20)

Next, differentiating and using Eq. (12) gives:

$J{\dot{\omega }}_e=-S\left(\omega \right)J\omega +{\psi }_1\left(\sigma \right)p+u+J\left[\ddot{\eta }{c}_2^{bo}-\dot{\eta }S\left({\omega }_{bo}\right)c_2^{bo}+k_1\dot{\sigma }\right]$   (21)

where $\dot{\sigma }=0.25B\left(\sigma \right){\omega }_{bo}$

The remaining part of the derivation of the control law is similar to Lee and Singh,²² in which quaternions have been used as attitude parameters. Of course, differences arise in the computation of the regressor matrix by the use of MRP. Therefore, the derivation will be presented briefly.

Let s be the Laplace variable or a differential operator. By adding and subtracting $J\left[k_2{\omega }_e+k_3\left(s+\alpha \right)\sigma \right]$ in Eq. (21), and defining:

${\Psi }_{2p}=-S\left(\omega \right)J\omega +J\left[\ddot{\eta }{c}_2^{bo}-\dot{\eta }S\left({\omega }_r\right)c_2+k_1\dot{\sigma }+k_2{\omega }_e+k_3\left(s+\alpha \right)\sigma \right]$

and $\Psi ={\Psi }_1+{\Psi }_2\in R^{3\times 9}$ , one obtains:

${\dot{\omega }}_e=J^{-1}\left[\Psi p+u\right]-k_2{\omega }_e-k_3\left(s+\alpha \right)\sigma$   (22)

where α, k₂, and k₃ are positive design parameters.

For the design of control input, a filtered version of Eq. (22), using a transfer function $H(s)={\left(s+\alpha \right)}^{-1}$ , is considered. The filtered signals satisfy the following equations:

${\dot{\Psi }}_f=-\alpha {\Psi }_f+\Psi$   (23)

${\dot{\omega }}_{ef}=-\alpha {\omega }_{ef}+{\omega }_e$   (24)

${\dot{u}}_f=-\alpha u_f+u$   (25)

Then, filtering both sides of Eq. (22) with H(s), gives:

${\dot{\omega }}_{ef}=J^{-1}\left[{\Psi }_{fp}+u_f\right]-k_2{\omega }_{ef}-k_3\sigma$   (26)

Now, in view of Eq. (26), u_f is chosen as:

$u_f=-{\Psi }_f\left(\widehat{p}+\beta \left({\omega }_{ef},{\Psi }_f\right)\right)$   (27)

where $\widehat{p}+\beta$ is the net estimate of the unknown parameter vector p. The component β is an algebraic vector function, and is the partial estimate of p. This choice of full estimate $(\widehat{p}+\beta )$ differs from the parameter estimate of CEA systems. In CEA systems, β is zero. The use of an algebraic function in the net estimate provides stronger stability properties in the closed-loop system.

Define the parameter error as $z=\widehat{p}+\beta -p$ . Then, substituting the control signal in Eq. (26) gives:

${\dot{\omega }}_{ef}=-J^{-1}{\Psi }_{f}z-k_2{\omega }_{ef}-k_3\sigma$   (28)

For stability analysis, consider a Lyapunov function:

$W_s=W_1+\left[{\omega }_{ef}^T{\omega }_{ef}/2\right]$

With the choice of $k_3+k_2-\alpha =0$ , after some manipulations, one can show that²²:

${\dot{W}}_s\le -\frac{1}{2}\left[\left(k_1+2k_3\right){\Vert \sigma \Vert }^2+k_2{\Vert {\omega }_{ef}\Vert }^2\right]+\left(\frac{k_1+k_2}{2k_1{k}_2}\right){\Vert J^{-1}{\Psi }_{f}z\Vert }^2$   (29)

Parameter estimation

Now, the derivation of parameter estimate is considered. The algebraic component β is chosen as:

$\beta =\gamma {\Psi }_f^T{\omega }_{ef},\gamma >0$   (30)

For the derivation of an update law for $\widehat{p}$ , consider the dynamics of the parameter error $z=\widehat{p}+\beta -p$ . Its derivative using Eq. (28) takes the form:

$\dot{z}=\dot{\widehat{p}}+\gamma {\Psi }_f^T{\omega }_{ef}+\gamma {\Psi }_f^T\left[-J^{-1}{\Psi }_{f}z-k_2{\omega }_{ef}-k_3\sigma \right]$   (31)

where one has ${\dot{\Psi }}_f=-\alpha {\Psi }_f+\Psi$ from Eq. (23). Now, an update law is selected as:

$\dot{\widehat{p}}=-\gamma {\dot{\Psi }}_f^T{\omega }_{ef}-\gamma {\Psi }_f^T\left[-k_2{\omega }_{ef}-k_3\sigma \right]$   (32)

Next, substituting Eq. (32) in (31) gives:

$\dot{z}=-\gamma {\Psi }_f^T{J}^{-1}{\Psi }_{f}z$   (33)

To examine the stability of the estimator, consider a Lyapunov function $W_e=v{\gamma }^{-1}{z}^{T}z/2$ with v > 0. Its derivative is:

$W_e=-v{z}^T{\Psi }_f^T{J}^{-1}{\Psi }_{f}z\le -v{\lambda }_{\min }\left(J^{-1}\right){\Vert {\Psi }_{f}z\Vert }^2$   (34)

where ${\lambda }_{\min }\left(J^{-1}\right)$ and ${\lambda }_{\max }\left(J^{-1}\right)$ denote minimum and maximum eigenvalues of $J^{-1}$ , respectively. Since ${\dot{W}}_e\le 0$ , it follows that z is bounded.

Closed-loop system stability

Now, the stability of the closed-loop system is examined. For this purpose, consider a composite Lyapunov function:

$W\left(q,{\omega }_{ef},z\right)=W_s\left(q,{\omega }_{ef}\right)+W_e\left(z\right)$   (35)

Using Eqs.(29) and (34), after some simplification, the derivative of W takes the form:

$\dot{W}\left(q,{\omega }_{ef},z\right)\le -\frac{1}{2}\left[\left(k_1+2k_3\right){\Vert \sigma \Vert }^2+k_2{\Vert {\omega }_{ef}\Vert }^2\right]+\left[\frac{k_1+k_2}{2k_1{k}_2}{\lambda }_{\max }^2\left(J^{-1}\right)-v{\lambda }_{\min }\left(J^{-1}\right)\right]{\Vert {\Psi }_{f}z\Vert }^2$   (36)

Note that v is a free parameter. Thus, for a sufficiently large v, there exists l^* > 0 such that:

$\dot{W}\le -\frac{1}{2}\left[\left(k_1+2k_3\right){\Vert \sigma \Vert }^2+k_2{\Vert {\omega }_{ef}\Vert }^2\right]+-l^{\ast }{\Vert {\Psi }_{f}z\Vert }^2\le 0$   (37)

Because W is positive definite and $\dot{W}\le 0$ , the signals σ, ${\omega }_v$ , z, and ${\omega }_{ef}$ are bounded. Of course, the boundedness of the filtered signal ${\omega }_{ef}$ implies that the input ${\omega }_e$ is bounded. This also implies the boundedness of $\omega$ . Thus, all the signals in the closed-loop system are bounded. Now, based on the boundedness of the derivatives of the signals, using Barbalat's lemma, one can prove that $\left(\sigma ,{\omega }_{ef},{\Psi }_{f}z\right)$ converge to zero. Furthermore, using arguments similar to those of Lee and Singh,²² one shows that σ and ${\omega }_{bo}=\omega -C^{bo}\left(\sigma \right){\omega }_o$ asymptotically converge to zero. Thus, the controller accomplishes nadir pointing control.

Remark 1: It is interesting to note that in the closed-loop system, the trajectories converge to a manifold ℳ_a defined as:

$M_a=\left\{\left({\Psi }_f,z\right):{\Psi }_{f}z=0\right\}$   (38)

This property of the NCEA system is not possible in CEA systems using the classical update law.

Now, for the implementation of the controller, computation of u from u_f is considered. Using Eqs. (25) and (27) gives:

$u={\dot{u}}_f+\alpha u_f=-{\dot{\Psi }}_f\left(\widehat{p}+\beta \right)-{\Psi }_f\left(\dot{\widehat{p}}+\dot{\beta }\right)-\alpha {\Psi }_f\left(\widehat{p}+\beta \right)$   (39)

Computing the derivative of β given in Eq. (30) and using Eqs. (23) and (32) in (39) gives the control law:

$u=-\Psi \left(\widehat{p}+\beta \right)-\gamma {\Psi }_f{\Psi }_f^T\left\{\left(k_2-\alpha \right){\omega }_{ef}+k_3\sigma +{\omega }_e\right\}$   (40)

This completes the design of the controller based on MRP attitude parameters.

This section presents the results of simulation. It is assumed that the satellite is in an equatorial elliptic orbit around asteroid 433 Eros. Simulation is done using the MRP control law as well as the I&I-based adaptive control law of Ref.²²–designed for quaternion vector $\left(q_a={\left(q^T,q_4\right)}^T\in R^4,q={\left(q_1,q_2,q_3\right)}^T\right)$ control. The quaternions satisfy:26

$q=\sin \left(\Phi /2\right)\widehat{e};q_4=\cos \left(\Phi /2\right);q_a^T{q}_a=1$

The MRP vector σ is defined in terms of quaternions as follows:

${\sigma }_i=q_i{\left(1+q_4\right)}^{-1},i=1,2,3$

It is assumed that (J₁, J₂, J₃) = (33, 33, 50) [Kg.m²], and the mass of the spacecraft is 600 [kg]. The remaining parameters of the model are: r₀ = 9:933 [km], C₂₀ = -0.0878, and C₂₂ = 0.0439.²² The gravitational parameter of 433 Eros and its rotation rate used for simulation are μ = 4.4650×10^-4 [km³/s²] and Ω = 3:312×10^-4[rad/s], respectively. The radial distance R_c and the orbital rate are:

$R_c\left(\eta \right)=\frac{a\left(1-e^2\right)}{1+e\cos \eta };\dot{\eta }=\left(\sqrt{\frac{\mu }{p_h^3}}\right){\left(1+e\cos \eta \right)}^2$

where a is the semi-major axis, e is the eccentricity, and $p_h=a(1-e^2)$ is the semilatus rectum. The initial conditions are q_i(0) = 0.5, (i = 1, .., 4) and ω(0) = (0.0004, 0.0004, 0.0004)^T [rad/s]. Thus, one has σ_i(0) = 0.5/1.5, (i = 1, 2, 3).

The selected feedback gains are k₁ = 0.1, k₂ = 0.3; k₃ = 0.2, and the filter parameter α is 0.5. The adaptation gain is set as γ = 5500. The initial value of the parameter estimate is arbitrarily set as $\widehat{p}(0)=0_{9\times 1}$ . The filter initial values are ${\omega }_{ef}(0)=0_{3\times 1}$ and ${\Psi }_f(0)=0_{3\times 9}$ .

It is assumed that the spacecraft is in a prograde elliptic orbit. The semi-major axis is 40 [km] and eccentricity is 0.3 or 0.4. It should be noted that for the purpose of comparison, the design parameters of this controller have been set equal to those of Ref.²², which was designed for quaternion control.

Case A. Adaptive MRP and quaternion control of spacecraft in prograde elliptic orbits: e = 0.3, 0.4, a = 40 [km], d = 0

The simulated responses of the closed-loop systems for MRP (left column) and quaternions (right column) control for (a = 40 [km], e = 0.3, d(t) = 0) are shown in Figure 2. It is observed that σ and q converge to zero in about 30 and 20 [sec], respectively. Also, q₄ converges to one. The maximum magnitudes (u_max, ω_max) of (u, ω) are ([1.2369, 1.2012, 1.5021]^T [Nm], [5.1234, 4.6384, 4.7175]^T [deg/s]) for σ control, and ([2.6971, 2.5942, 3.3546]^T [Nm], [8.0291, 7.4175, 7.6238]^T [deg/s]) for q_a control, respectively.

Figure 2 Adaptive control of spacecraft in prograde elliptic orbit (R_c = 40 [km], e = 0.3; d = 0): (a) MRP control (b) Quaternion control.

Simulation was also done for larger eccentricity (e = 0.4). The responses are shown in Figure 3. One observes that despite large eccentricity, responses are somewhat similar to those of Figure 2. It is seen in Figures 2 & 3 that for both eccentricities, compared with the quaternion-based control law, the MRP-based control system achieves attitude control with smaller control magnitude, but requires larger settling time. Additionally, the convergence of trajectories to the manifold ℳ_a for σ control is smoother (see the plots for $\Vert {\Psi }_{f}z\Vert$  in Figures 2 and 3).

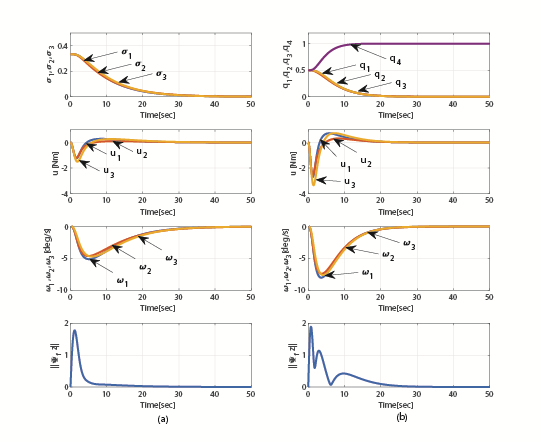
Figure 3 Adaptive control of spacecraft in prograde elliptic orbit (R_c = 40 [km], e = 0.4; d = 0): (a) MRP control (b) Quaternion control.

Case B. Adaptive MRP and quaternion control in prograde elliptic orbit: e = 0.4, a = 40 [km], d ≠ 0

For simulation, random signals d_i, (i = 1, 2, 3), were generated by passing white noise through a filter transfer function $\frac{5\times {10}^{-4}}{s^2+0.6s+1}$ . The mean value and the variance of the white noise were assumed to be 0 and 1, respectively. The signals d_i, (i = 1, 2, 3), are shown in Figure 4. (Disturbance torque caused by solar radiation pressure can be expected to be of similar order (10^-3) [Nm] or even smaller.⁴) Simulated responses for (a = 40 [km], e = 0.4) are shown in Figure 4. It is observed that σ and q converge to zero despite the parametric uncertainties and random disturbance torque.

Figure 4 Adaptive control of spacecraft in prograde elliptic orbit (R_c = 40 [km], e = 0.4; d ≠ 0): (a) MRP control (b) Quaternion control.

In this paper, an I&I-based adaptive controller was designed for the attitude control of spacecraft orbiting around asteroid. For the representation of attitude, the modified Rodrigues parameters were used. The inertia matrix and the gravity field parameters were assumed to be unknown. By the Lyapunov analysis, the convergence of the MRPs and system's trajectories to the origin and to the manifold ℳ_a, respectively, was accomplished. Also, for the purpose of comparison, the quaternion-based NCEA law²² was simulated. The responses showed that with identical design parameters in these two control laws, the MRP-based control law required smaller control magnitude and accomplished smoother convergence of trajectories to the manifold ℳ_a, but required larger settling time for the attitude trajectories.

None.

The authors declare that there is no conflict of interest.

1. Misra AK, Panchenko Y. Attitude dynamics of satellites orbiting an asteroid. Journal of the Astronautical Sciences. 2006;(54)(3-4):369‒381.
2. Kumar KD. Attitude dynamics and control of satellites orbiting rotating asteroids. Acta Mechanica. 2008;198(1-2):99‒118.
3. Wang Y, Xu S. Analysis of the attitude dynamics of a spacecraft on a stationary orbit around an asteroid via Poincare section. Aerospace Science and Technology. 2014;39:538‒545.
4. Kikuchi S, Howell KC, Tsuda Y, et al. Orbit-attitude coupled motion around small bodies: Sun-synchronous orbits with sun-tracking attitude motion. Acta Astronautica. 2017;140:34‒48.
5. Bandyopadhyay S, Chung SJ, Hadaegh FY. Nonlinear attitude control of spacecraft with a large captured object. J Guid Control Dyn. 2016;39(4):754‒769.
6. Lee D, Sanyal AK, Butcher EA, et al. Almost global asymptotic tracking control for spacecraft body-fixed hovering over an asteroid. Aerospace Science and Technology. 2014;38:105‒115.
7. Lee D, Sanyal AK, Butcher EA, et al. Finite-time control for spacecraft body-fixed hovering over an asteroid. IEEE Trans Aerosp Electronic Systems. 2015;51(1):506‒520.
8. Lee D, Vukovich, G. Adaptive sliding mode control for spacecraft body-fixed hovering in the proximity of an asteroid. Aerospace Science and Technology. 2015;46:471‒483.
9. Vukovich G, Gui H. Robust adaptive tracking of rigid-body motion with application to asteroid proximity operations. IEEE Trans on Aerospace and Electronic Systems. 2017;53(1):419‒430.
10. Reyhanoglu M, Kamran N, Takahiro K. Orbital and attitude control of a spacecraft around an asteroid. 12th International Conference on Control, Automation and Systems: Jeju Island, South Korea; 2012.
11. Wang Y, Xu S. Body-fixed orbit-attitude hovering control over an asteroid using non-canonical Hamiltonian structure. Acta Astronautica. 2015;117:450‒468.
12. Astolfi A, Ortega R. Immersion and invariance: A new tool for stabilization and adaptive control of nonlinear systems. IEEE Trans Autom Control. 2003;48(4):590‒606.
13. Astolfi A, Karagiannis D, Ortega R. Nonlinear and adaptive control with applications. Springer-Verlag: London; 2008.
14. Ioannou P, Sun J. Robust adaptive control. Prentice-Hall: Englewood Cliffs, NJ; 2013.
15. Seo D, Akella MR. High-performance spacecraft adaptive attitude-tracking control through attracting-manifold design. J Guid Control Dyn. 2008;31(4):884‒891.
16. Yang S, Akella MR, Mazenc F. Dynamically scaled immersion and invariance adaptive control for Euler-Lagrange mechanical system. J Guid Control Dyn. 2017;40(11):2844‒2856.
17. Seo D. Fast adaptive pose tracking control for satellites via dual quaternion upon non-certainty equivalence principle. Acta Astronautica. 2015;115:32‒39.
18. Wen H, Yue X, Li P, et al. Fast spacecraft adaptive attitude tracking control through immersion and invariance design. Acta Astronautica. 2017;139:77‒84.
19. Zhang B, Cai Y. Immersion and invariance vased adaptive backstepping control for body-fixed hovering over an asteroid. IEEE Access. 2019;7:34850‒34861.
20. Lee KW, Singh SN. Immersion-and invariance-based adaptive control of asteroidorbiting and - hovering spacecraft. J Astronaut Sci. 2019;66:537‒553.
21. Lee KW, Singh SN. Noncertainty-equivalence adaptive attitude control of satellite orbiting around an asteroid. Acta Astronautica. 2019;161:24‒39.
22. Lee KW, Singh SN. Quaternion-based adaptive attitude control of asteroid-orbiting spacecraft via immersion and invariance. Acta Astronautica. 2020;167:164‒180.
23. Lee KW, Singh SN. Adaptive and Super-Twisting Adaptive Spacecraft Orbit Control Around Asteroids. ASCE Journal of Aerospace Engineering. 2019;32(4):04019042.
24. Lee KW, Singh SN. Generalized Composite Noncertainty-Equivalence Adaptive Control of Orbiting Spacecraft in Vicinity of Asteroid. The Journal of the Astronautical Sciences. 2020;67(3):1021‒1043.
25. Schaub H, Junkins JL. Stereographic orientation parameters for attitude dynamics: A generalization of the Rodrigues parameters. Journal of Astronautical Sciences. 1996;44(1):1‒19.
26. Schaub H, Junkins JL. Analytical mechanics of space systems. 3rd ed. AIAA Education Series: Reston, VA; 2014.
27. Crassidis JL, Markley FL. Sliding mode control using modified Rodrigues parameters. Journal of Guidance, Control, and Dynamics. 1996;19(6):1381‒1383.
28. Schaub H, Akella MR, Junkins JL. Adaptive control of nonlinear attitude motions realizing linear closed loop dynamics. Journal of Guidance, Control, and Dynamics. 2001;24(1):95‒100.
29. Tsiotras P. Further passivity results for the attitude control problem. Journal of Guidance, Control, and Dynamics. 1998;43(11):1597‒1600.