The introduction contains a summary of modern provisions that make it impossible to interpret many phenomena occurring in diode laser systems on the basis of commonly accepted physical conceptions. The work demonstrates their inadequacy. The goal and tasks of studies have been formulated. Analysis of a solid and its internal structure (crystal) is provided. It is demonstrated that interaction of plane surface clusters determines the surface structure of solids, while the interaction between three-dimensional clusters determines the internal structure of solids (crystals). Each atom inside the crystal interacts with the first, second and third coordination layer. The value of conduction band energy is determined by displacement of the ionization boundary. For implementation of diode lasers, the distribution of electrons by Fermi-Dirac energies must have a sufficiently diffused maximum.

N-conductivity emerges when ionization of negative ions occurs, the energy of affinity of which is located near the conduction band. Р-conductivity is determined by ionization of negative ions, the energy of affinity of which is located near the valence band. Р-n junction is mostly formed when two-atom molecules enter the band gap. In this case, some of the atoms have an affinity for an electron with the value of such affinity located is near the conduction band, while other atoms have an affinity for an electron near the valence band. Interband transition energy contains three components: 1 – Fermi level position energy; 2 – energy of external applied electrical field, and 3 – induced energy formed by positive charge in the valence band.

Generation of laser emission takes place when two-atom molecules are adsorbed on the surface of the semiconductor crystal, in which atoms have an affinity to the electron for some of the atoms near the conduction band and for other atoms near the valence band. Maximum emission intensity occurs when external applied electrical voltage fully compensates the energy of affinity to the electron located near the conduction band.

Keywords: negative ion, energy of affinity, n-conductivity, p-conductivity, n-p-conductivity, heterostructure, diode laser

Semiconductor or diode lasers are used in various fields of technology. They include, for example, production of telemetry sensors, optical altitude meters, aiming devices, range finders and pyrometers. Production of optic fiber systems, coherent communication systems, data storage and transfer systems. Protection systems, quantum cryptography, automatics. Production of laser printers, video projectors, laser indicators, scanners, CD players. Optical metrology and spectroscopy, surgery, dentistry, cosmetology and therapy. Treatment of materials, water purification, control of chemical reactions. Industrial machine-building and industrial sorting. Production of ignition system and beam weapons. In the future, the scope of application of semiconductor lasers will be expanding intensively, and the problems with correct interpretation of physical principles of operation of such systems will emerge.

It is commonly believed today that operation of diode lasers is based on the recombination luminescence arising on the р-n junctions. In works,^1–3 it is demonstrated that р-n junction is formed by negative ions that are introduced in the base of the semiconductor crystal in the form of two-atom molecules or heterostructures, the atoms of which have both low and high energy of affinity to the electron. Р-n junction is controlled by means of changing temperature, supplying electrical voltage, as well as optical emission, or injection and electric breakdown. Using three-level and four-level energy system formed in diode lasers in accordance with the known energy structure in the band gap, one assumes that recombination luminescence occurs in diode lasers.⁴

In case of formation of a p-n junction between bands with р-conductivity or n-conductivity, a thin layer with a thickness of ~ 10 μm is formed, which shall be considered to be a barrier layer. This layer is created by means of high-temperature diffusion of two-atom structures or heterostructures into the crystal base of the diode generator. If an external electric field is applied to the system, thickness of the barrier layer will depend on the direction of the field. When the plus is applied to the р-semiconductor, and the minus is applied to the n-semiconductor, the thickness of the barrier layer is reduced or becomes equal to zero. In this case, electric current will flow through the p-n junction. This direction of external electric field is known as straight. If the direction of the external field coincides with the direction of the electric field, the thickness of the barrier layer increases, and the current will not flow through the p-n junction.

When a short-term current impulse is passed in forward direction, a quick recombination luminescence will occur in the p-n junction area when external voltage is switched off. If such conductor is placed in the resonator, generation will occur. During operation of diode lasers, it was found that the semiconductor base on which impurities are applied must have a band gap in the electron density distribution within the crystal, i.e. the Fermi level separating the valence band from the conduction band must have an energy value of ~ 2 eV or more. The base in diode lasers is mostly formed by purified aluminum or germanium, or, in some cases, silicon, in which the energy width of the band gap amounts to 1.687, 2.44 and 2.5 eV respectively.⁵

The descriptive nature of emergence of energy levels in the diode laser does not make it possible to substantiate physical essence of emergence of generation and carry out computer modeling of the effect of various impurities and different influences on the generation process. Therefore, the objective emerged: to find out what particles form crystals, to determine the source energy levels that emerge in the band gap of the base materials, as well as energy levels of p-dopants and n-dopants, and use the results as a basis to amend the theory of operation of diode lasers taking into account the levels of energies of negative ions in the band gap.

The objective can be achieved by solving the following tasks:

1. Determine the surface structure of pure aluminum, germanium, and silicon, as well as particles (molecules) that form the crystal.
2. Provide grounds for introduction of certain impurity molecules into the crystal in order to obtain the specified generation frequency.
3. Determine the cause of emergence of the barrier layer if there are negative ions.
4. Determine optimal conditions for obtaining set generation frequency.
5. Develop the mechanism of formation of laser emission with determination of its power taking into account the structure of the crystal and presence of negative ions in the band gap.

Let us examine the tasks set to substantiate the aforementioned objective.

Surface structure of aluminum, germanium, and silicon

In electronics, crystals of aluminum, germanium, and silicon are used as the basis. This is due to the fact that only these crystals have a wide range of energies in the Fermi-Dirac distribution. Aluminum, germanium and silicon crystals are formed by three-atom molecules. Three-atom molecules on the surface and inside the crystal are combined into clusters. The form of these clusters was defined in⁶ and is shown in Figure 1а.

Dotted lines are used to indicate the molecules, the centers of which contain an excessive positive charge. Other molecules contain an excessive negative charge in their centers. A surface cluster of three-atom molecules looks like a snowflake with electric charges alternating in sign. On the surface of the solid, such snowflakes engage with each other to form an electron sequence alternating in sign in the solid. When a scanning tunnel microscope was created in 1981, and the Si(111) silicon surface was obtained,⁷ the structure of the silicon surface theoretically calculated in⁶ completely coincided with the experimentally obtained surface. Theoretically calculated structure of surface of the silicon crystal formed by three-atom molecules is shown in Figure 1b, where dark color indicates holes through which inclusions are embedded into the crystal. As a comparison, Figure 1c contains an image of an experimentally obtained silicon (111) surface.⁶ The theory is completely in line with the experiment.

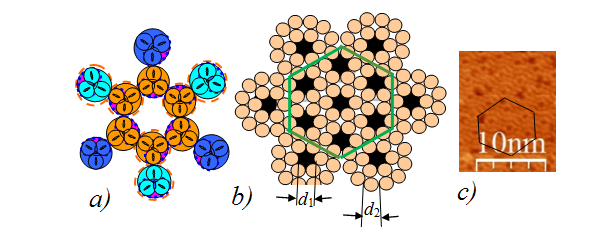
Figure 1 a) surface cluster of three-atom molecules; b) surface of the crystal with deposited clusters of two-atom molecules; c) experiment.

Internal structure of crystals is examined by means of X-ray diffraction analysis. X-ray diffraction (XRD) analysis is based on the scattering of X-rays in course of interaction with individual atoms. XRD analysis made it possible to determine the nature of distribution of atoms inside the crystal. However, experimental data and theoretical calculation performed in^8,9 shows that crystals are formed by clusters composed of molecules. An aluminum crystal is a facet-centered structure, while germanium and silicon are diamond structures formed by means of embedding two facet-centered structures into each other. Therefore, aluminum crystals, like germanium and silicon crystals, are formed by three-atom molecules. This conclusion has been proven experimentally and theoretically for a silicon crystal with diamond structure.⁹

Inside crystals, the edge between clusters disappears, as a result of which each atom interacts with atoms of the immediate environment that create the first coordination layer. At the same time, interaction with second and third coordination layers is implemented. Therefore, each atom inside the crystal interacts with a great number of atoms, i.e. collective interaction of atoms is implemented. In course of such interaction, each valence electron of the atom belongs to many atoms as a result of continuous electron exchange. It means that all valence electrons in the crystal are kind of free and have no spin. In crystals of all three types, the maximum distribution of electrons by Fermi-Dirac energies is significantly diffused. For other crystals, this maximum is fairly sharp and located near the Fermi level. It turns out that single ions of atoms inside the crystal create a crystal lattice, while free electrons are located between ions in the electric field of a positively charged crystal lattice. Therefore, free electrons inside the crystal are in a potential well. Internal distribution of electrons for most crystals was obtained experimentally by diffusion of X-rays of К-band and L-band. Theory of such distribution was developed in^8,9 Experimental results and theoretical calculations are given for aluminum in Figure 2, for germanium- in Figure 3, for silicon- in Figure 4. For all three crystals, a band gap is formed, which is located between the conduction band and the valence band.

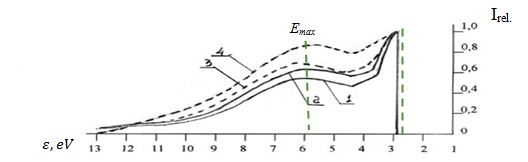
Figure 2 Distribution of electrons by energies inside crystal lattice of aluminum; 1 – theoretical calculation; 2 – theoretical calculation considering U-shaped hardware broadening with energy of 0.05 eV; 3 – experimental distribution from the L3-band and 4 – from the К-band.

Figure 3 Distribution of electron density by energies for a germanium crystal.

Figure 4 Distribution of electron density by energies for silicon.

The width of the conduction band is determined by displacement of the ionization boundary and is free from electrons. Presence of such zone in the main crystal of the laser is a necessary element for operation of the quantum generator. In the absence of external electric voltage, all electrons inside the crystal are contained in the valence band and inside the potential well, the size of which is determined by the position of the Fermi level relative to the conduction band. Maximum distribution of electric density by energies inside aluminum, germanium and silicon crystals corresponds to the ionization energy of atoms of this element. In the conduction band, electrons are absent. However, current flows through aluminum, germanium and silicon quite efficiently. This means that in metals and in semiconductors the electric current is formed by conduction current and displacement current.¹⁰ At the same time, tangential intensity of the electric field of displacement current is equal to the normal component of the electromagnetic wave.¹⁰ The analysis performed demonstrates that the surface structure and the internal structure of the solid in the form of the crystal are completely different. The experimental proof is given in.¹¹

A scanning tunnel microscope has a resolution of ~1Å, which makes it possible to measure the flow of electrons from the surface of a single atom. Applied external field of no more than 2 eV is not capable of passing through the potential barrier determined by operation of the output, which amounts to 4.244, 4.60 and 4.8 eV for aluminum, germanium, and silicon (111) surface respectively.⁹ In order for the electron to pass through such energy in the Binning and Rohrer scanning microscope, it was suggested that it happens due to the emergence of the tunnel effect. However, after thorough analysis of spectral characteristics obtained in different points of the surface and on surfaces of different materials,¹² it was discovered that atoms with an affinity to electrons on surfaces of a number of solids, whether separate or located within molecules (and, therefore, in clusters), remain in the form of negative ions. At the same time, their ionization energy must be located near the maximum of the function of distribution of valence electrons by energies inside the crystal,¹² which ensures a rather efficient exchange between atoms on the surface of the solid and distribution of electron density inside the crystal of the Fermi-Dirac electron cloud.

Atoms whose ionization energy level is sufficiently distant from the maximum of the Fermi-Dirac distribution function do not capture electrons directly from the crystal. Capture of electrons can occur during spontaneous transition of electrons from the conduction band to the valence band. Near the valence band, the capture of electrons by negative ions occurs only when an electric current occurs between the conduction band and the valence band. In this case, all atoms with affinity to the electron remain as negative ions, and the positively charged holes in the valence band compensate for these charges. Besides, there is an excess of positive charge in the valence band, which is determined by ionization of negative ions near the conduction band.

The energy diagram of the band gap is shown in Figure 5a. The concentration of electrons in the conduction band with overcoming the band gap on the basis of the Maxwell-Boltzmann law is^1–3:

$n_F=n_{a,0}exp\left[-\frac{E_F}{k_{b}T}\left(1-\frac{e^2\Delta {\phi }^2}{E_F^2}\right)\right]$   (1)

Where $n_{a,0}$ – concentration of negative ions on the surface of the main semiconductor crystal; $E_F$ – Fermi level energy of the main crystal; $k_b$ – Boltzmann's constant; $\Delta \phi$ – applied difference of potentials between the conduction band and the valence band.

In semiconductors, field emission occurs from separate atoms in the form of negative ions.¹² It is necessary to find out which negative ions are donors creating n-conductivity and which are acceptors creating p-conductivity. Such division is purely conventional. Electric conductivity is determined not by concentration of free electrons and free positive holes, but by the value of concentration of dipole electric moments¹⁰ formed under the effect of various external factors.

P-dopants and n-dopants in diode lasers

Each crystal in a solid is formed by clusters that contain large numbers of atoms. Interaction of clusters within a crystal leads to formation of a latticed cluster structure. Depending on the arrangement of clusters, cavities are formed between them. Cavities 4.05R0, 3R0, 1.5R0, 0.5R0 and 0.3092R0 emerge in facet-centered structure of aluminum and in diamond structure of germanium and silicon⁸ where R0 is the distance between particles in the cluster, i.e. the lattice constant. Cavities 4.05R0, 3R0, and 0.3092R0 are spherical, while other cavities are slot-shaped and located chaotically relative to each other. They were previously believed to be cracks. Presence of slot-shaped cavities of a relatively large size in the crystal is the reason of formation of dislocation, and diffusion of atoms and two-atom molecules occurs through these cavities into the crystal for a sufficient depth.

Therefore, formation of the p-n junction is associated not with embedding the impurity atoms into the main crystal, but with a simple penetration into the crystal via slot-shaped cavities of the same size as 1.5R₀two-atom molecules, while slots with a size of 0.5R₀ can only be used for penetration of atoms, i.e., crystal slots inside the crystal are filled with deposited impurities. Penetration of atoms and molecules through the surface layer into the crystal occurs only via pillar-shaped cavities, the size of which is ~ 8, as determined according to experimental data (the size of the black dots in Figure 1c). With such dimensions, even large heterostructures will penetrate into the crystal, where, while interacting with the surface inside micro-cracks in the crystal, they decompose into separate atoms. If these atoms have affinity to the electron, they stay as negative ions. Therefore, in diode lasers one tends to completely fill the pillar-shaped cavities by sputtering different types of heterostructures on the cathode and anode, and to obtain a smooth surface without "quantum wells". Then the area between the conduction band and the valence band will correspond exactly to the energy of the band transition. Electrons that appeared in the conduction band will be at the surface of the beginning of the pillar-shaped cavities.

Molecules and even clusters deposit on the surface of the crystal between pillar-shaped cavities. For example, two-atom molecules of indium on the surface of silicon have connection energy of ~ 0.366 eV¹¹ and remain in the form of neutral molecules. Laser radiation that can emerge in this case is examined in.¹³ Negative ions of atoms and molecules on the surface of the crystal are not formed. As a rule, three-atom molecules have a higher electron affinity than atoms and two-atom molecules. Therefore, a double electric layer is formed on the crystal surface.

N-conductivity emerges when an impurity is introduced with affinity energy near the conduction band. In this case, the impurity introduced serves as a donor. It means that free electrons emerge in the conduction band that are capable under effect of the applied electric field to transfer electric charge inside the band gap and excite induced emissions. Transfer of electrons between energy levels is not an electric current and is associated with emission of electromagnetic waves. Electric current emerges as a result of the translational motion of free electrons, creating conduction current, or as a result of distribution of energy of the electromagnetic field in accordance with the Pointing vector¹⁰ if there are free electric dipoles in the medium.

The electron in the conduction band does not move and remains at rest. At the same time, it has no spin and in combination with the valence band creates an additional electric moment, the concentration of which determines electric conductivity.¹⁰ Internal interconnection between electric current and radiation of electromagnetic waves with determination of the dipole electric moment is not clearly defined, which causes confusion.

As a result, with passage of electric current, dipole electric moments in combination determine electric conductivity of the environment and are not destroyed, while in case of emergence of electromagnetic waves dipole electric moments are fully destroyed, and the energy of interaction between charges in the dipole is released by radiation in the form of an electromagnetic wave. The rule for spin-based selection in this case for semiconductor lasers has the following form ∆S=0.

Concentration of electrons in the conduction band in accordance with the Maxwell-Boltzmann law is found by the formula^1–3:

$P=\frac{k_1{n}_{e}h\upsilon \Delta S\Delta l{{\displaystyle \int }}_0^{L}exp\left(-k_{2}l\right)dl}{\tau }$   (2)

Where $n_{a,0}$ is the concentration of impurity atoms, $E{A}_d$ is the energy of affinity of atoms of the n-dopant to the electron. Other designations are shown above.

The obtained excess of electrons in the conduction band corresponds to identical deficiency of electrons in the valence band. At the same time, additional electric moment emerges between the valence band and the conduction band. It causes an increase in the relative dielectric permeability and an increase in the conductivity current between contacts of the main semiconductor. At the same time, in accordance with the previously adopted terminology, n-conductivity emerges in the diode laser semiconductor (Figure 5b) which serves as the basis in the diode laser.

Р-conductivity is realized when impurity is introduced into the band gap of the dielectric, the atoms of which have an affinity energy to the electron near the valence band. In this case, atoms of the impurity turn into negative ions, and electron deficiency emerges in the valence band, while the surface of the main crystal receives an additional positive charge. Concentration of these positive charges will be:

$n_i^{+}=n_{a,0}exp\left[-\frac{\left(E_F-E{A}_a\right)}{k_{b}T}\left(1-\frac{e^2\Delta {\phi }^2}{{\langle E_F-E{A}_a\rangle }^2}\right)\right]$   (3)

Where energy of affinity of p-dopant atoms to the electron.

As a result, an additional electric moment will emerge between the valence band and negative ions of the impurity atoms, which will cause an increase in the relative dielectric permeability and an increase in the electric conductivity current between contacts of the main semiconductor. In accordance with the previously adopted terminology, р-conductivity will emerge in the main semiconductor (Figure 5c). Р-n junction is implemented when different atoms enter the band gap, in which some atoms have an affinity to the electron, the value of which is located near the conduction band, while other atoms have an affinity to the electron near the valence band. As a rule, two-atom molecules or heterostructures that are a complex of separate atoms in the form of a three-atom structure are used for this purpose. As a result, additional energy levels emerge in the band gap near the conduction band, as well as near the valence band at a distance equal to the sum of radii of atoms of impurity and atoms of the main crystal (Figure 5d). If atoms with affinity to the electron are inside the band gap, then such atoms stay in the form of negative ions. And together with the valence band they create excess dipole electrical moments in the band gap.

Figure 5 a) band gap; b) n-conductivity; c) р-conductivity and d) – p-n junction.

In order to achieve the maximum concentration of free electrons in the conduction band, it is necessary to apply a potential difference equal to the electron affinity energy of atoms near the conduction band to the р-n junction. If a potentials difference greater that the affinity to the electron is applied, the concentration of electrons in the conduction band will decrease dramatically because the ionization of donor negative ions will stop. The transition energy of free electrons from the conduction band to the valence band consists of three components: Fermi energy (ЕF), the applied potential difference (∆φ), and the induced potential difference, which is created by the excess positive charge of the valence band:

$\Delta E_R=E_F+\Delta \phi e+e{E}_{э}\Delta l.$   (4)

Here electric field intensity inside the band gap Еэ is created by external electric field and internal distribution of electric charges in the band gap of the main crystal of the diode laser, and ∆l – the thickness of the barrier layer. The induced intensity of electric field near the valence band in general is determined as follows: 

$E_{э}=\frac{\left(n_d+n_{ak}+n_a+n_e+n_i\right)e}{{\epsilon }_r{\epsilon }_0}l.$   (5)

Where $n_d$ – surface concentration of n-dopants; $n_{ak}$ – surface concentration of p-dopants; ${\epsilon }_r$ – absolute dielectric permeability, and ${\epsilon }_0$ – absolute dielectric permeability of vacuum introduced by Sommerfield and l – the size of the band gap. Other values are defined above. When determining the energy of laser transition in the electric field intensity inside the p-n junction, the effect of the charged surface of p-dopant and n-dopant levels of negative ions can be disregarded, as in this case the electron during movement in the band gap passes through the negatively charged lattice structure of adsorbed atoms. As a result, the electron passing through the negative lattice structure is first decelerated and then accelerated, i.e. the energy lost when entering the lattice negative structure is fully restored after leaving this structure. In normal conditions, temperature population of the conduction band may always be disregarded.

As the interzone transition emerges in the free space between molecules, ${\epsilon }_r=1$ . As a result, conducted intensity of the electric field emerging inside the band gap will be transformed as:

$E_{э}=\frac{n_e^{-}+n_i^{+}}{{\epsilon }_0}el.$   (6)

Let us find out how this situation affects passing of electric current through the band gap with formation of a barrier layer.

Barrier layer

The band gap in the energy representation with p-dopants and n-dopants is shown in (Figure 6). On the surface of a semiconductor crystal in certain conditions, n-dopants and p-dopants impurity atoms take the form of negative ions and act as a barrier layer. Surface density of charges is permanent and does not depend on internal or external interactions. This is due to the fact that under the effect of an external applied field, negative ions can give their electrons out but at the same time n-dopants and p-dopants collect electrons from the valence band, and the lost electrons are restored by the impurities. Such process of electron exchange by negative ions with the main crystal is due to the fact that the ionization energy of impurity atoms coincides with the maximum of distribution of electrons by energies in the main crystal of aluminum, germanium or silicon. As a result, an effective electron exchange takes place, and the circulation of internal electrons in the crystal with n-dopants and p-dopants is implemented. Therefore, diode lasers can operate both continuously and in pulsed mode.

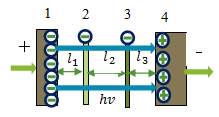
Figure 6 General energy representation of the diode laser: 1 – conduction band, l1–n-band; 2 – level of affinity to the electron of the n-dopant, l2 – emission band; 3 – level of affinity to the electron of the p-dopant, l3– p-band, 4 – valence band.

Distances between energy levels in the band gap shown in Figure 6 are as follows:

$l_1=r_1+r_2; l_2=\Delta l; l_3=r_3+r_1;$   (7)

where $r_1$ – radius of atoms of the main crystal; $r_2$ –radius of atoms of the n-dopant; $r_3$ – radius of atoms of the p-dopant in the two-atom molecule. All these data can be found in various physics reference books. For example, values of distance for the base of aluminum $r_1$ (Al)=1.43 Å, germanium $r_1$ (Ge)=1.39, silicon $r_1$ (Si)=1.18 Å.⁹ For two-atom ZnS, ZnO, CdS и CdSe molecules, radii for zinc, sulfur and oxygen are as follows: $r_2$ (Zn)=1.37 $\AA$ $r_3$ (S)=1.04Å, $r_4$ (O)=0.74Å and $r_5$ (Se)=1.60Å. If no resonator is used, the emission will correspond to LED. In this case, the emission spectrum must be formed by joint effect of formulas (1), (2) and (3); i.e. regular luminescence occurs with the width of the spectrum which is formed under the effect of variation of the external supply voltage.

When such system is placed in the resonator, the concentration of electrons in the conduction or valence band should be determined by one of formulae (2) or (3), and the maximum emission frequency by formula (4). Emission spectrum width does not depend on variation in the supply voltage and is determined by the lifetime of the excited state. In this case, the spectral line of emission should be narrow enough. Such a situation has been experimentally discovered and is shown in Figure 7. In the ZnSe molecule, zinc has affinity of ~ 0.5 eV, and the difference (E_F – E_Aa) ~ 2.44-2.21= 0.23 eV. In the absence of resonator, regular spontaneous emission occurs for such molecule, the intensity of which is determined by ionization of n-dopants and p-dopants. With large values of applied voltage, emission intensity will be mostly defined by ionization of n-dopants, with low voltages - mostly by ionization of p-dopants. Therefore, radiation luminescence spectrum will be defined by combined ionization of n-dopants and p-dopants.

Figure 7 ZnSe emission spectrum: 1 – luminescence, 2 – generation.

In the resonator, ZnSe molecule generates emission in the maximum when the applied voltage reaches 0.5 V. With such voltage, the wavelength will be minimal due to inclusion of induced intensity of the electric field near the valence band.

Molecules ZnS and ZnO generate emission in the near-ultraviolet region with a wavelength in the maximum of $\lambda \left(ZnS\right)=315 and337$ nm; $\text{λ}\left(ZnO\right)=375 and 383$ nm. Affinity to the electron for zinc is unknown, for sulfur-  Generation spectrum for introduction of ZnS and ZnO molecules into germanium crystal is shown in Figure 8.

Figure 8 Generation spectrum of molecules ZnS and ZnO.

In the first and second case, generation occurs at two frequencies, and these cases differ significantly in terms of intensity. Generation for ZnS molecule emerges at wavelengths of 315 nm and 337 nm. Laser radiation intensity at 315 nm wavelength is significantly smaller than for 337 nm wavelength. This is due to the fact that the intensity of laser emission is mostly defined by ionization of n-dopants, while ionization of p-dopants causes an increase in the conducted field intensity near the valence band and reduces the laser emission wavelength.

For ZnO molecule, the situation is opposite: 375 nm wavelength has a greater intensity than 383 nm wavelength. In this case, the energy of affinity for zinc is smaller than the difference of energies between the value of the Fermi energy and the energy of affinity of the p-dopant, i.e.$E{A}_d<E_F-E{A}_a\mathrm{..}$  Therefore, at first the energy level of the negative ion near the conduction band is populated, and as the supply voltage increases, in accordance with equation (3) it passes through the maximum near the p-band and then drops sharply. Laser emission stops, and the conducted field strength near the valence band is reduced, while the wavelength is increased.

Using Planck's equation for 315 nm wavelength, the difference of energies passed by the electron during interzone transition will amount to $\Delta E_{ZnS}=\frac{hc}{\text{λ}\left(ZnS\right)}=3.941 eV$ , for 337 nm wavelength- $\Delta E_{ZnS}=\frac{hc}{\text{λ}\left(\text{ZnO}\right)}=3.684 eV$ . It is clear that in order to obtain such energies, the main crystal must be used with the maximum Fermi energy. Maximum Fermi energy is found in germanium and silicon crystals. Germanium is frequently used in laser equipment. Where is additional energy during interzonal transition taken from? No answer!

Therefore, it is necessary to analyze more thoroughly the p-n junction, the diagram of which is shown in Figure 5d and Figure 6. Surface concentration of charged particles is determined by the number of introduced molecules (atoms) on the surface of the main semiconductor crystal and inside the crystal through slot-shaped cavities. Moreover, deposition of two-atom molecules occurs in depressions between clusters and the surface layer of the solid. All defects of the crystal disrupt the surface and block slot-shaped cavities and depressions on the surface of the crystal in the solid. Therefore, in production of electronic equipment using crystals with surface (111), large number of defected goods emerges when a clean surface (111) of sufficient size is selected. This can be clearly seen in Fig. 1c, where the concentration of crystal defects is very significant.

Concentrations of electrons $n_e^{-}$ and $n_i^{+}$ are determined using formulae (2) and (3). For this, it is necessary to know the energy of affinity to the electron. Harrie Massey (Harrie Massey. 1976), based on the fact that atoms of zinc and cadmium have fully closed electron shells, believed that these atoms shall have no affinity to the electron. Actually, closed S- and D-shells interact with each other. If we take the Hund's rule into account, the interaction between these shells must be significant, and the displacement relative to nucleus of atom of two S-electrons must be noticeable. Specific calculation of the dipole electric moment and the energy of affinity to the electron was performed for zinc and cadmium according to the method specified in.¹⁵ The results are shown in Table 1.

Every negative ion radius is associated with specific values of dipole moment and affinity to the electron. For zinc and cadmium, in case of atom radius exceeding 1.85Å, affinity to the electron has a positive value, which contradicts its definition. With a radius less than 1,85Å , affinity to the electron has a negative value. Therefore, zinc and cadmium atoms in the band gap must be in the form of negative ions. It is important to determine the radius of free zinc and cadmium atoms.

For this purpose, let us use equation (4). In order for laser emission to be realized on ZnS molecules, the electron must be carried from one level to another energy level separated from the first one by 3.68 eV, in a laser with evaporation of ZnO molecules by 3.31 eV energy value. In the laser with evaporation of two-atom molecules on germanium in equation (4), the width of the band gap corresponds to the germanium crystal and is equal to 2.44 eV. Voltage applied to the p-n junction is controlled with a sufficient accuracy and does not exceed the affinity energy, while the electric field intensity in the band gap is created mostly by the positively charged surface of the main semiconductor crystal. If the electron affinity energy level of an atom near the valence band does not exceed the difference of potentials applied to the p-n junction, the positive charge conducted in the valence band will be exactly equal to the charge conducted by atoms near the conductivity band, i.e.$n_i^{+}=n_e^{-}$

If impurity atoms near the valence band have ionization energy that is significantly distant from the maximum of the electron distribution function, such atoms are not capable of efficient capture of electrons from the valence band of the main semiconductor crystal. In order for such atoms to be neutral and not turn into negative ions at relatively low temperatures, their energy of affinity must significantly exceed the difference of potentials applied to the p-n junction. Then the positive charge will not be conducted on the valence band plane. In this case, density of the positive charge on the valence band boundary will be formed exclusively due to capture of electrons by atoms near the conduction band, and the resulting conducted intensity of electric field in the band gap (6) will decrease exactly twice. Such situation occurs for oxygen atoms when they are located near the valence band of the germanium crystal. Ionization energy 13.6 eV is significantly distant from the Fermi-Dirac electron distribution function maximum, and the affinity energy 1.69 eV is also significantly distant from the Fermi level ~2.44 eV.

As ZnS and ZnO molecules are applied on the same germanium crystal, as a result of selection of the value of affinity to the electron for zinc in the ZnS molecule, the value of electric field intensity in the band gap is found using formula (4). In the same conditions, for the ZnO molecule conducted intensity of the electric field in the band gap determined using the formula (6) will be two times smaller. By selecting the electron affinity for zinc according to formula (4), the laser transition energy for sputtering ZnO molecules is found. As it turned out, with the affinity energy for zinc equal to 0.4975 eV, the energy of the laser transition corresponded to the experimental value. The radius of the zinc atom for ZnS and ZnO amounted to 1.79Å. Radius of the zinc atom calculated using the Slater method¹⁶ amounted to ~ 1.89Å, according to the data from the reference book¹⁷- to 1.533Å; i.e. radii of free atoms differ significantly when calculated with the help of different methods. Therefore, radii of neutral atoms shall be found using various experimental data that are in some way connected to the radius of neutral atom, as is done in this article.

Therefore, study of diode lasers taking into account presence of negative ions in the band gap makes is possible to correctly explain emergence of laser emission inside the crystal. On the surface of a solid, certain two-atom molecules can also produce laser emission. This option is considered in.¹³ Conditions for emergence of generation are fairly complicated and difficult to implement. Therefore, another route was chosen, which implied introduction of impurities into the base of crystals of metals (aluminum) and semiconductors (germanium and silicon). In this case, it is necessary to control the conditions for emergence of generation.

Optimal conditions for obtaining set generation frequency

New physical concepts of emergence of laser radiation in semiconductors with involvement of negative ions make it possible to interpret differently emergence of emission on the р-n junction. Both р-conductivity and n-conductivity are determined by presence of impurities with an affinity to the electron in the band gap of the main crystal, and their atom ionization energy must correspond to the maximum distribution of Fermi-Dirac electron density in the main crystal. In this case, impurity atoms may remain in the form of negative ions and create a negatively charged plane inside the band gap. If such plane is located near the conduction band, free electrons will emerge in it under external effect caused by ionization of negative ions. If negative ions are closely connected to Fermi-Dirac distribution of the main crystal, the number of electrons given out by them during ionization to the conduction band determined according to formula (2) will be equal to the number of electrons compensated during exchange with the valence band. In this case, an additional positive charge will be formed in the valence band, which will be equal to the one formed in the conduction band, $n_e^{-}=n_e^{+}$ .

If the impurity in the main crystal is located near the valence band, and the impurity atoms have an affinity to the electron, the capture of electrons by negative ions takes place. In this case, a negatively charged flat layer will emerge near the valence band, and the same value of positive charge will be conducted in the main crystal. At the same time, additional concentration of conducted positive charges in the valence band is determined according to formula (3). If conducted concentration of positive charges is determined according to (3), three cases shall be considered:

$I-E{A}_a>E_F;\text{ II}-E{A}_d\approx E_F-E{A}_a:\text{ III}-E{A}_d<E_F-E{A}_a.$   (8)

In the first case, negative ions of the p-dopant do not take part in creation of negative ions, and they shall not be taken into account in formula (6) when determining conducted intensity of the electrical field near the surface of the main crystal. In this case, conducted intensity of the electric field near the valence band will only be determined by $n_e^{-}$ - concentration.

In the second case, $n_e^{-}\approx n_i^{+}$ conducted intensity near the valence band will be increased exactly twice as compared to the first case. This situation is mostly used in diode quantum generators.

In the third case, energy of affinity of p-dopant atoms is located at a sufficient distance from the Fermi level, somewhere in the middle of the band gap. In this case, at low temperatures, such an impurity does not take part in additional conduction of a positive charge in the valence band; i.e. a more complex version of the first case is implemented. Such conditions emerge on the example of the two-atom molecule of ZnO considered above.

Therefore, the optimal option for realization of the laser diode at set generation frequency occurs in conditions where atoms of the n-dopant have an affinity to the electron, the value of which is not sufficiently distant from the conduction band, and the affinity to the electron of the p-dopant atoms is also insignificantly distant from the Fermi level. The following condition is met in this case:

Such situation occurs when CdS molecules are sputtered on the germanium base.  In this case, emission frequency is approximately equal to the interzone energy. In this case, according to (8), the electron affinity for the CdS molecule will amount to: $E{A}_d\approx 2.44-2.077=0.363 eV$ , i.e. approximately 0.4 eV. A similar situation occurs for gallium nitride and aluminum-gallium nitride. Since the electron affinity for nitrogen ~ 2.776 eV¹⁴ and is greater than the band gap of germanium, the nitrogen will be inside the valence band as a negative ion in which the electron is in a bound state and there will be an additional increase of free positive charges in the valence band. Therefore, a laser on gallium nitride based on formulae (4) and (5) is obtained in the ultraviolet region.

After selection of the two-atom molecule that makes it possible to achieve the required generation frequency, it is necessary to determine the power that can be realized at this generation frequency and the method of achieving the maximum emission energy at this frequency.

Semiconductor laser emission power

In works^4,18 and etc. the laser emission power was measured with a special photosensitive device, while the total electric power consumed by the laser was determined by means of measuring electric current and voltage supplied to the laser. Physical processes implemented in case of emergence of generation remained unclear. Therefore, in each specific case of application of two-atom molecules or heterostructures in the diode laser for achievement of set frequency and power of generation, it is necessary to measure the generation frequency and identify optimal conditions of achieving the maximum emission power by experimental means. This is a result of the fact that the physical model of operation of a diode laser was formed purely in qualitative terms on the basis of the idea about free electrons and positively charged holes.

It was hard to imagine earlier that atoms introduced into the crystal may remain on its surface in the form of negative ions, while the crystal itself is formed by clusters. Only after the complete substantiation of negative ions formation in 2016,¹⁹ the importance of negative ions in many spheres of science and technology became apparent,²⁰ including electronics,^1–3 while in 2004,⁸ it was proven that crystals are built by clusters. It was previously believed on the basis of the X-ray diffraction analysis that they were formed by atoms, as diffusion of X-rays takes place on atoms. The arrangement of atoms obtained by such method corresponds to a cluster as opposed to a crystal. Based on this, we will consider how the power of the generated emission is formed in diode lasers taking into account the structure of the crystal or presence of negative ions in the band gap.

It was experimentally established that heterostructures are initially evaporated onto the surface of the main semiconductor solid state body; the heterostructures are composed of three different atoms that mutually compensate induced dipole electrical moments. Such a structure has no conductivity. Electric current does not flow through such structure. After that, the next layer of two-atom molecules is applied on the heterostructure. This layer creates conditions for passage of forced emission formed by two-atom molecules without significant obstacles, while electrical current passes over lateral surfaces that have a different structure.¹¹ Many researchers have arrived at this conclusion purely through experimentation. Forced emission occurs only when induced electrical dipoles are mutually compensated. Electrical current flows through such structure, while there are no restrictions for complete dissolution of dipoles with emission output. This condition for emergence of induced emission was not clearly defined.

Therefore, we will examine formation of the active region. Two-atom molecules (or heterostructures) are applied onto germanium or silicone semiconductor base, and deep penetration of atoms into the base is achieved due to diffusion. Evaporation of heterostructures with an increase of donor atoms is performed to enhance the power of the laser, while heterostructures with an increase in the acceptor atoms is used to enhance the frequency of forced emission. Implementation of this process in the laser is shown in Figure 9.

Figure 9 Diagram of a diode laser.

Active region d ~ 1 μm is filled with two-atom molecules. With complete filling, significant dispersal of forced emission takes place. The laser heats up effectively, and generation occurs at extremely low temperatures. As a result, the structure is significantly complicated. This fault was eliminated by application of two-atom GaAs molecules in the central part of the laser as a strip with a thickness of δ~ 3-5 μm, the entire thickness being 100-200 μm. This strip serves as an active medium, with electrical current flowing over its lateral surface.

For specific assessment of emission power, let us consider a laser with a double heterostructure separated with a gallium arsenide strip shown in Figure 10. In such laser, maximum size of the luminescence strip is 0.747 μm.⁴ Transition energy of this wave is 2.66 eV, and the life cycle of the electron in excited state is τ=1.557

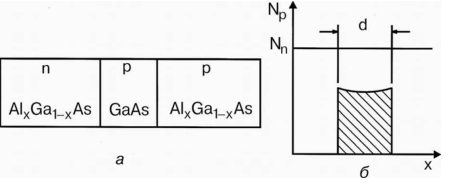
Figure 10 Double heterostructure with a gallium arsenide strip: a) heterostructure, b) active strip thickness.

Penetration of two-atom molecules and heterostructures through the surface into the core of the germanium crystal occurs only via pillar-shaped cavities of the surface layer (Figure 1b), while the arrangement of clusters inside the crystal prevents penetration of two-atom molecules into depressions under the surface of the crystal. Moreover, output emission is absorbed according to the exponential Bouguer law. Therefore, double heterostructure diode laser emission power can be represented as follows:

$P=\frac{k_1{n}_{e}h\upsilon \Delta S\Delta l{{\displaystyle \int }}_0^{L}exp\left(-k_{2}l\right)dl}{\tau }$   (9)

Here, $k_1$ is the probability of passing through the surface for penetration of two-atom molecules of gallium arsenide and heterostructures inside the crystal; $k_2$ is the absorption factor of the semiconductor laser, $h\upsilon$ is the energy of the emitting quantum; ΔS=L∙δ- transverse laser emission area; Δl- is the depth of penetration of impurity into the base semiconductor crystal due to diffusion to the depth of the germanium cluster; τ is the lifetime of free electrons in the conductivity region.

The probabilityon the basis of fig. 1с for germanium is 0.127. Depth of penetration of aluminum, gallium and phosphor atoms does not exceed the size of the germanium cluster and amounts to ~ 3R₀, where R₀=2∙1.39Å. In case of laser emission, self-absorption can be neglected, and in this case, the emission power for GaAs molecules with the length L = 500 μm and the width δ = 5 μm (Figure 9) and the concentration of free electrons ne = 1021 m-3 in (averaged value of experimental data) will amount to ≈ 17.3 mW. Such laser power values are absolutely acceptable and conform to experimental data.⁴ The maximum possible value of ne =1022 m-3. More than 10 active tracks can be evaporated on a width of 200 μm. In this case, the laser power will exceed 2 W. If more than a hundred of these structures are evaporated on a common base with a common resonator, a laser with more than a kilowatt of power can be produced.

Perform assessment of passage of electrical current. Current density is:

$J=n_{e}e{v}_e$   (10)

Electron mobility ve can be found if the structure of the surface formed by two-atom molecules is known. Gallium arsenide molecule is formed by two atoms with a significant difference in the size of atoms. The surface of such molecules is shown in Figure 11. If a voltage of 5 V is applied to such surface with a thickness of 1 μm, then the effective speed of movement over such surface with the size of the free zone between GaAs $\Delta x\approx {\mathrm{1.63.10}}^{-9 }M$ molecules will amount to

$v_e=\sqrt{\frac{4}{5}.\frac{e\Delta \phi \Delta x}{d{m}_e}}\approx {\mathrm{5.8.10}}^{4}m/s$   (11)

Figure 11 Fragment of the structure of surface of two-atom molecules with atoms of different size.

Electrical current is:$I=J.2L.d\approx 9.3 мА.$ If the concentration of introduced inclusions is maximized, and the number of active tracks is 10 or more, the value of the electrical current will increase by two orders of magnitude and amount to ~ 1 А. Performed theoretical assessment of the emission power and the value of electrical current on the basis of attracting formation of negative ions and their ionization in the forbidden zone of the main crystal of the diode laser is in fairly close correlation with experimental data. Accurate theoretical calculations are impossible in principle, as the technology of production of lasers and chips for them is carefully protected. However, a lot still needs to be studied in this direction in order to ensure production of semiconductor equipment based on strictly defined theoretical base with computer simulation as opposed to intuition.

Therefore, by using the modern physics of solid structure formed by clusters, where impurities inside the crystal may take form of negative ions, it has become possible to provide a completely different substantiation of the diode laser operation principle. As a result, new ideas on the work of such systems were developed. Let us present here the main provisions obtained in development of the new theory of operation of diode lasers:

1. The introduction contains a summary of all negative provisions that make it impossible to interpret many phenomena occurring in diode laser systems on the basis of commonly accepted physical conceptions.
2. Surface and internal crystal in solids are formed differently. Interaction of plane surface clusters determines the surface structure of solids, while the interaction between three-dimensional clusters determines the internal structure of solids (crystals).
3. Surface and three-dimensional clusters are formed by two-atom or three-atom molecules.
4. Dense arrangement of atoms inside the crystal leads to collective interaction between atoms. Each atom interacts with the first, second and third coordination layer. The number of atoms in each layer is determined by the structure of the crystal, and the electrons within the crystal are distributed by energy according to the Fermi-Dirac function.
5. The value of conduction band energy is determined by displacement of the ionization boundary. This makes it possible to prevent scattering of free electrons formed in the conduction band during ionization of negative ions.
6. For implementation of diode lasers, the distribution of electrons by Fermi-Dirac energies must have a sufficiently diffused maximum. Aluminum, germanium and silicon possess such distribution. This is a unique case, and this is why only these solids are used in semiconductor electronics.
7. N-conductivity emerges when ionization of negative ions occurs, the energy of affinity of which is located near the conduction band.
8. Р-conductivity is determined by ionization of negative ions, the energy of affinity of which is located near the valence band.
9. Р-n junction is mostly formed when two-atom molecules enter the band gap. In this case, some of the atoms have an affinity for an electron with the value of such affinity located is near the conduction band, while other atoms have an affinity for an electron near the valence band.
10. Interband transition energy contains three components: 1 – Fermi level position energy; 2 – energy of external applied electrical field, and 3 – induced energy formed by positive charge of the valence band.
11. The barrier layer is created by negative ions of n-dopants and p-dopants on the surface of the semiconductor crystal.
12. Luminescence occurs on semiconductor crystals when mostly n-dopants are applied on their surface near the conduction band. Luminescence spectrum width is determined by combined ionization of negative ions of n-dopants and p-dopants.
13. Generation takes place when two-atom molecules or heterostructures are adsorbed on the surface of the semiconductor crystal, in which atoms have an affinity to the electron for some of the atoms near the conduction band and for other atoms near the valence band. Maximum emission intensity occurs when external applied electrical voltage fully compensates the energy of affinity to the electron of atoms located near the conduction band.

None.

The author declares that there is no conflict of interest.

None.

1. Gretchikhin LI. Formation of p-, n-conductivity in semiconductors. Military technical courier. Scientific Periodical of the Ministry of Defense of the Republic of Serbia. 2018;2(6):424–428.
2. Gretchikhin LI. Formation of p-, n-conductivity and p-n junction. Strengthening technologies and coatings. 2018;14(5):231–238.
3. Gretchikhin LI. Formation of p-, n-conductivity by negative ions. The Aviation Herald. 2022;6:8–16.
4. Gribkovsky VP. Semiconductor lasers. Minsk University publication. 1988.
5. Babichev AI, Babushkina NA, Bratkovsky AM. et al. Physical values: Reference book. Ed. In: Grigoriev IS, Meilikhov ED, editors. Energoatomizdat. 1991. 1232 p.
6. Gretchikhin LI, Latushkina SD, Komarovskaya VM, et al. Cluster structure of silicon and structure of its surface. Strengthening technologies and coatings. 2015;9:9–16.
7. Binnig G, Rohrer H, Gerber C, et al. Surface studies by scanning tunneling microscopy. Phys Rev Lett. 1982;49(1):57–61.
8. Gretchikhin LI. Physics of nanoparticles and nanotechnologies. General foundations, mechanical, thermal and emission properties. Minsk: Tekhnoprint. 2004;399.
9. Gretchikhin LI. Nanoparticles and nanotechnologies. Minsk: Law and Economics FLLC. 2008;406.
10. Gretchikhin LI. Physics Electricity and magnetism Modern electrodynamics. Minsk: Law and Economics FLLC. 2008;302.
11. Gretchikhin LI, Shmermbekk Y. Interaction of evaporated particles with solid surface. The Aviation Herald. 2021;5:21–28.
12. Shmermbekk Y, Migas DB, Gutkovsky AI, et al. Negative ions in field emission. Strengthening technologies and coatings. 2020;3.
13. Gretchikhin LI. Nano-level analysis of semiconductor quantum generators of type А3В5. Science and Technology Bulletin. Science Journal of the Ministry of Defence of the Republic of Serbia. 2015;63(2)9–29.
14. Harrie Massey. Negative ions. Cambridge University Press; Cambridge: 1976. 759 p.
15. Gretchikhin LI. Built-in and induced electric dipole moments in complex atomic systems and in the diatomic molecules. The Aviation Herald. 2020;2:28–34.
16. Slater JC. Quantum Theory of Molecules and Solids. New York: McGraw-Hill; 1965-1967.
17. Radtsig AA, Smirnov BM. Reference book on atomic and molecular physics. Atomizdat. 1980. 240 p.
18. Gretchikhin LI, Minko LY. On the analogy of physical processes occurring in a pulsed discharge and under the action of concentrated laser radiation. Technical Physics. 1967;37.
19. Gretchikhin LI, Komarovskaya VM. Negative ions of atoms, diatomic and triatomic molecules. Military technical Courier. Scientific Periodical of the Ministry of Defence of the Republic of Serbia. 2016;64(2):447–464.
20. Gretchikhin LI. Negative ions and their role in the development of science and technology. Military technical Courier. Scientific Periodical of the Ministry of Defence of the Republic of Serbia. 2018;66(4):847–863.