Unmanned aerial vehicles (UAVs) are widely applied. However, for a fuller fulfillment of UAVs’ potential, it is important to understand the promising directions of their evolution. This was carried out based on of the modern thermodynamics and the constructal law of design and evolution (1995) developed by the famous American physicist A. Bejan. The evolution of conventional airplanes obeys this law and is in line with the evolution of animal locomotion.  However, UAV design and parameters are different from the design and parameters of conventional airplanes. The performed analysis shows that UAV evolution also obeys the constructal law. This allows determining the rational ratios between the masses of UAV subsystems and other parameters, such as operational range or speed. As with other moving objects, those ratios may be achieved during the process of evolution or design as a compromise between required large payload mass and long operational range.  At unchanged vehicle’s maximum takeoff and a required large payload masses the maximal operational range is the criterion that describes UAVs’ movements’ in space efficiency. In order to increase this range it is necessary to increase the UAV’s energy supply (the fuel / battery mass) by reducing the mass of other components and the propulsion systems’ (PS) efficiency. However reserves for reducing payload or body masses have already been exhausted. Therefore, the required compromise may only be established by perfection of PSs. Electric PSs may have a significant potential and benefits. These PSs may have five cardinal architectures: all electric; hybrid electric; heat engines-electric generators (full or partial). The analysis showed that the maximal of operational range and correspondingly the maximal efficiency of UAVs’ movement may be achieved by using PSs based on the high power density microturbines (MTG) or simple plug-in series hybrid PSs also based on the MTGs.

Keywords: evolution, constructal law, unmanned aerial vehicles, propulsion system, microturbine generator

UAV, unmanned aerial vehicles; PS, propulsion systems; REG, range extender generator; ICE, internal combustion engine; MTG, microturbine generator

S                    operational range, km  

M_U                 payload mass, kg

M_V                   vehicle’s maximal takeoff mass, kg

M_PS                PS mass (engine + fuel / battery, transmission, propeller etc.), kg

V_V                  vehicle’s speed, m/s

P_PS                             propulsion system power, kW

η_PS                 propulsion system efficiency

P_E                     engine power, kW

L/D                drag ratio

HD_E               hybridization degree

e_BAT                battery specific energy, kWh/kg

e_F                   fuel specific energy, kWh/kg

Today, UAVs are widely applied in various military and civilian applications. Today, there are more than 1000 UAV models and concepts.^1,2 From 1933-1936 (the first mass produced UAV OQ-2 Radioplane) their design and performance parameters have been constantly improving. It is well known that the efficiency of UAVs using depends on the possibilities to provide the required payload mass M_U and on increasing the operational range S.^1,2

These most important parameters are conflicting and depend on numerous design factors. For a fuller fulfillment of UAVs’ potential, it is important to understand the promising directions of their evolution at the design or modernization stages.  Only at these stages the rational correlation between payload mass and operational range may be provided in order to overcome contradictions and to realize the reserves of their increasing. An analysis of design practice shows the presence of various UAV evolution vectors and the diversity of their structures and especially their engines.^1,2 The most probable direction of evolution may be established based on modern thermodynamics and the constructal law of design and evolution (1995) developed by the famous American physicist A. Bejan (Duke University).^3-5 This law is rapidly expanding field in physics, the theory of evolution, biology, technology and social sciences. It was successfully used to analyze the evolution of airplanes (2014)³ but was never used to analyze UAV evolution.

1. Bejan states the following. The evolution of various vehicles, including conventional airplanes is in line with the evolution of animal locomotion and that it is predictable from his constructal law. The evolution of vehicles illustrates the evolutionary design of the “human-and-machine species” as it moves and spreads on Earth: farther, faster, more efficiently, and with greater lasting power (sustainability). The main result is that the conventional airplanes must obey theoretical rules that unite them with the birds and other animals. For example, the larger airplanes are faster, more efficient as vehicles, and have greater operational ranges, etc.

This law is an expansion of the first and second laws of thermodynamics as applied to living and non-living systems. In other words, from the point of view of thermodynamics, the evolution of vehicles, including airplanes, has two aspects. On the one hand, it goes in the direction of maximal generation of entropy that will be emitted to the environment during the performance of the useful work. On the other hand, it goes in the direction of the minimal generation of entropy inside the vehicle to reduce energy loss during this performance of the useful work. This also applies to the evolution of subsystems (vehicle’s components) sizes and efficiency. So the constructal law has two main consequences:^3-5

1. The mass of the subsystems and other parameters, such as operational range and speed should be proportional to the vehicles body size. For example, the engine’s mass is proportional to the vehicles body size: this scaling is analogous to animal design, where the mass of the motive organs (muscle, heart, lung) is also proportional to the body size. Also fuel mass should be proportional to the vehicles body size;
2. The main direction of evolution in subsystem design is their miniaturization.

However, the UAV design and performance parameters are very different from the design and parameters of conventional airplanes. The following hypothesis is advanced. UAV evolution also obeys the constructal law.

This allows determining the rational ratios between the masses of their subsystems and other parameters, such as operational range or speed. As with other moving objects, those ratios may be achieved during the process of evolution or design as a compromise between required large payload mass and long operational range. It is well known that in order to increase the UAVs’ efficiency it is necessary to increase their energy supply (the fuel/battery mass) by reducing the mass of other components and to increase the propulsion systems’ (PS) efficiency. However reserves for reducing payload or body masses have already been exhausted. Therefore, a required compromise may only be established by perfection of PS. These features will be discussed in detail below.

The aim, objectives, objects, subject and methods of research                     

The aim of research is to determine the directions of the UAV evolution in order to increase their efficiency based on perfection of PSs.

Objectives of research

1. confirm that the UAV evolution obeys the constructal law of design and evolution;
2. formulate the conditions of choosing rational UAV parameters in order to increase their efficiency;
3. use the basic patterns of the UAV evolution in order to determine the rational parameters of their systems;
4. determine the rational electric PS architectures and parameters in order to increase UAV efficiency.

Objects of research are UAVs (maximal takeoff mass M_V =700 kg) with different electric propulsion systems. These PSs may have five cardinal architectures: all electric; hybrid electric; heat engines-electric generators (full or partial).^1,2,6,7 UAVs are complex technical systems for efficient energy conversion. Their PSs are important subsystems, but aren’t the independent objects of optimization. UAV PSs are significantly different from similar systems that are used in conventional aviation, for example, systems based on gas turbine engines. These PSs must produce not only mechanical energy, which is necessary for movement, but also a sufficient amount of electric energy which is required for UAV equipment’s (payload’s) operation. Considered electric PS may have significant potential and benefits.

The subject of research is the patterns of changing of UAV efficiency in a function of electric PS  architecture, components’ masses and efficiencies.

Statistical methods for analyzing more than 100 UAVs' parameters as functions of UAVs' takeoff masses were used to assess UAVs' compliance with the constructal law. Based on that, many rational values for various masses were established, including PS masses, as well as other parameters for medium UAVs.

The conditions for choosing rational UAV parameters that will increase UAV efficiency were formulated as follows. At an unchanged vehicle’s maximal takeoff mass M_V and a required large payload mass M_U the maximal operational range S in function of: PS architectures and components’ masses and efficiencies is the criterion which describes UAVs’ movements' in the space efficiency: M_V=idem; M_U=idem; S → max.

In order to increase this range it is necessary to increase UAVs' energy supply (the fuel / battery mass) and the propulsion systems' and their components' efficiencies.

The variety of PS architectures (all electric; hybrid electric; heat engines-electric generators) and their parameters (masses, efficiency and specific energy of motor, fuel / battery, transmission, propeller, etc) allows defining a rational architecture that fulfills the requirement S → max. Therefore, the required compromise between a required large payload mass and a long operational range may be established.

For the subsequent analysis, a simple simulation was used, details in our articles.^7-9 The simulation was based on UAV typical motion cycles and specific UAV parameters, such as drag ratio L/D≈10-11(Medium UAVs).^2,6,7 The required fuel/battery masses were calculated using real component performance values (specific power, efficiency, etc) for different electric propulsion systems,^6-8 Table 1, 2. Other electric PS components’ performances were: lithium-ion batteries (specific energy - up to 0,22  kWh/kg, efficiency up to 0,95);  electric motors (specific power-up to 2.5 kW/kg, efficiency up to 0,95); power electronic (specific power-up to 2,5 kW/kg, efficiency up to 0,98);  transmission and propeller  masses (specific power-up to 10-12 kW/kg).^2,6-9  

Hybrid electric PSs can be categorized based on the hybridization degree HD_E of their energy sources:^6-8  

HD_E=(e_BAT ⁕M_BAT)/(e_BAT ⁕M_BAT+ e_F ⁕M_F).

For PSs with all electric architectures (HD_E =1) a possible operational range is:   

S=(L/D) ⁕e_BAT ⁕η_PS ⁕(1/g )⁕ (M_BAT/M_V);

For PSs with heat engines-electric generators architectures (HD_E=0) a possible operational range is:        

S=(L/D) ⁕e_F ⁕η_PS ⁕(1/g )⁕ln [(1/(1-M_F/M_V)]_,

For hybrid electric PSs (0˂ HD_E˂1) the possible operational range was defined as the operational range for the HD_E value that produced the longest range.

A detailed analysis verified the proposed hypothesis. UAV evolution also obeys the constructal law of design and evolution. The speed V_V as a function of vehicle’s maximal takeoff mass M_V is located between birds' and conventional airplanes' speeds (Figure 1).

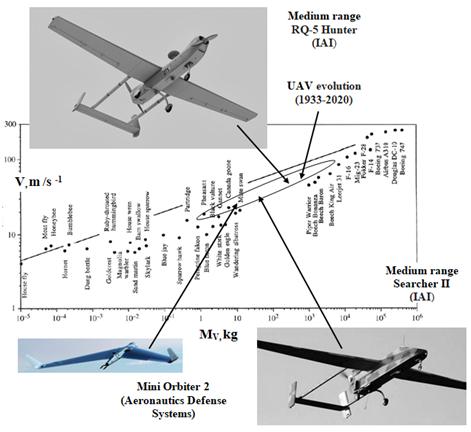
Figure 1 A.Bejan's constructal law of design and evolution:^2-4 UAV evolution also obeys this universal law.

According to the constructal law the direction of evolutions of components' masses (size), for example, PSs’ masses or their powers P_PS are determined by two opposing patterns of changing of entropy as a function of the mass or power (Figure 2).^3-5 On the one hand, there is a gain in reducing energy loss by increasing the engine's size. On the other hand, there is a loss because more energy is wasted carrying the engine as its size increases. A compromise, or minimal fuel consumption (Entropy Generation Minimum) is ensured with the optimal engine’s mass or power in relation to vehicle’s total mass.

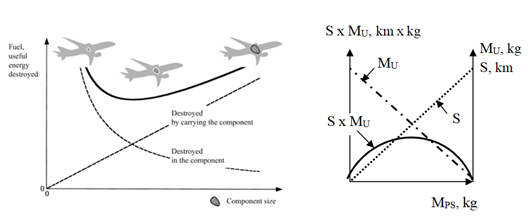
Figure 2 a-the constructal law’s consequence: сonstructal origin of “characteristic sizes”;^3-5 b-the qualitative pattern between propulsion system mass M_PS, operational range S and payload mass M_U.

During the 90 years-long history of UAV evolution an approximate proportionality has emerged between the following parameters (1) UAVs’ speed V_V (2) payload mass M_U (3) the propulsion systems power P_PS (4) operational range S,  and  vehicle’s takeoff mass M_V. The data are correlated in a statistically significant way, as:

V_V=16 M_V ^0,166 ;        M_U=0,1 M_V ^1,08;      P_PS=0,12 M_V ^0,97 ;     S=3 M_V ^0,84.

These relationships make it possible to determine UAV rational parameters such as vehicle’s takeoff mass M_V or the propulsion systems power P_PS, using the required UAV parameters such as payload mass M_U or operational range S. However, it is well-known that the reserves for reducing payload or glider masses due to miniaturization and usage of new lighter and more durable materials have already been exhausted.^1,2,6,7 Therefore, a compromise between required payload mass M_U and operational range S may only be established by changing PSs’ architectures, reducing PSs' and their components’ masses, and increasing their efficiencies and specific powers.

To determine the rational propulsion systems’ option, it is necessary to take into account the relationships between PS mass M_PS, operational range S and payload mass M_U at an unchanged vehicle’s maximal takeoff M_V. The qualitative relationships between PS mass M_PS, operational range S and payload mass M_U are simple and clear (Figure 2).⁷ While the M_PS increases, mainly due to higher fuel/battery mass, the operational range S also increases proportionally. However, the payload mass M_U also decreases proportionally as the operational range S increases. For UAVs, this compromise may correspond to the maximal transport work, proportional to: S x M_U. However, practice shows that the need to transport the required M_U can be achieved only by reducing the operating range S or runtime.

The simulation shows the possibility of increasing the operational range S to up to 300 km based on the example of  UAV (design stage)  with various  electric PSs’ architectures (all electric; hybrid electric; heat engines-electric generators) and its various parameters, such as  components’ masses, efficiencies and specific powers/energy.

Parameters: vehicle’s maximum takeoff mass M_V =700 kg; maximum allowable PS mass M_PS=300 kg (engine + fuel / battery, transmission, propeller etc.) , propulsion system power P_PS =100 kW.⁶ PSs must produce not only mechanical energy, which is necessary for movement, but also a sufficient amount of electric energy which is required for UAVs' equipment’s (payload’s) operation.

The results (Figure 3) present the following:  

1. Electric PSs provide a maximal operational range S of 40-50 km. Battery mass may be up to 250 kg;
2. Hybrid PSs based on the conventional light internal combustion engine (ICE) with power P_E≈40 kW may increase S to 180 km with M_PS up to 300 kg;
3. PSs based on the light ICE engine - generator (power P_E≈100 kW) and an adequate supply of fuel may increase S up to 250 km at M_PS up to need 300 kg;
4. PS based on the diesel- generator (power P_E≈100 kW) and an adequate supply of fuel also increases S up to 270 km at a required M_PS of up to 300 kg;
5. Simple plug-in series hybrid PS based on high power density MTG (power P_E≈40-50 kW) may effectively work at a steady state with a 100 kg battery and may provide S of up to 280 km, with a required M_PS of up to 300 kg;
6. PSs based on the high power density MTG (power P_E≈100 kW) may provide S of more than 300 km with M_PS of up to 270 kg. This may give the possibility of increasing the payload mass M_U by 15-20%. High efficiency, good starting properties, acceleration dynamics and low noise also may be achieved.

Figure 3 The relationship between operational range S and propulsion system mass M_PS as a function of PSs’ architectures. The vehicle’s maximum takeoff mass M_V=idem.

The following was established:

1. UAV evolution also obeys Bejan's universal constructal law of design and evolution. Relationships between (1) UAVs’ speed V_V (2) payload mass M_U (3) the propulsion systems power P_PS (4) operational range S and vehicle’s takeoff mass M_V were established. These patterns make it possible to determine UAV rational parameters at the design stage.
2. The reserves for reducing UAV payload or glider masses due to miniaturization and usage of new lighter and more durable materials have already been exhausted. Therefore, a compromise between the required payload mass M_U and the operational range S may only be established by changing PSs’ architectures, reducing PSs' and their components’ masses, and increasing their efficiencies and specific powers.
3. This compromise may be achieved in the most effective way by using electric PSs based on high power density microturbine generator (power P_E ≈ 100 kW) or simple plug-in series hybrid PSs also based on high power density MTG. These PSs may provide operational range S of 300 km or more. Electric PSs based on high power density MTG may also make it possible to increase the payload mass M_U by 15-20%. High efficiency, good starting properties, acceleration dynamics and low noise may also be achieved using these PSs.

None.

Authors declare that there is no conflict of interest.

1. Handbook of Unmanned Aerial Vehicles. Valavanis, K., Vachtsevanos, George J. Editors. Springer: Dordrecht; 2015.
2. Brelje B, Martins J.  Electric, hybrid, and turboelectric fixed-wing aircraft: A review of concepts, models, and design approaches. Progress in Aerospace Sciences. 2019;104:1–19.
3. Bejan A, Charles JD, Lorente S. The evolution of airplanes.  Journal of Applied Physics. 2014;116:044901.
4. Bejan A, Marden JH. Unifying  constructal theory for scale effects in running, swimming and flying.  J Exp Biol. 2006;209(Pt 2):238–248. 
5. Bejan A, Lorente S. Design with Constructal Theory. Wiley: Hoboken; 2008.
6. Ehsani M, Gao Y. Modern Electric, Hybrid Electric and Fuel Cell Vehicles: Fundamentals, Theory and Design. CRC Press: New York; 2010.
7. Arav B, Feldman D. Development of Propulsion system (PS) concept for different Unmanned Vehicles (UV). In: Tartakovsky L, editor. Proceedings 7th Conference on Propulsion Technologies for Unmanned Aerial Vehicles: Technion, Haifa; 2016. 52–54 p.
8. Arav B, Shulman R, Kozminykh V. Refinement of Hybrid Motor-transmission Set Using Micro Turbine Generator. Procedia Eng. 2015;129:166–170.
9. Arav B. Analysis of the concepts of hybrid transmission systems vehicles. Journal AAI. 2011;5:35–39.