For a heat engine working between two heat reservoirs, a hot reservoir at high temperature T_H and a cold reservoir at low temperature T_L, an effective temperature and an effective efficiency are introduced. The effective temperature is defined as the square root of the ratio between the net work output of the heat engine w_net and the SOT function (a new function introduced in this article). The SOT function is defined as the negative of the cyclic integral of the heat transfer change divided by the square of the temperature. The effective efficiency of the heat engine is defined (a novel definition) as one minus the ratio between the low temperature and the effective temperature. The effective temperature and the effective efficiency are worked out in details for the Carnot heat engine and the air standard cycles (Otto, Brayton, Stirling, and Ericsson). It was found for the considered cycles that the effective temperature is given by the expression and the effective efficiency is given by the expression $n_{eff}=1-\sqrt{\frac{T_L}{T_H}}$ for all the considered cycles. The importance of these two proposed measures is twofold: educational and they could be used as a quick tool by the designer.

For a heat engine working between two heat reservoirs, a hot reservoir at high temperature T_H and a cold temperature at low temperature T_L, what is the maximal achievable efficiency by the heat engine? This question was answered by Sadi Carnot at the beginning of the 19^th century by using methods of thermodynamics.^1-2 It was found that the maximal efficiency is limited by the Carnot efficiency $\left(n_C=1-\frac{T_L}{T_H}\right)$ . It is well known that the Carnot cycle is the most efficient cycle operating between these specified temperature limits. The Carnot cycle includes four branches: isentropic compression, isothermal heat addition, isentropic expansion and isothermal heat rejection.³ The Carnot cycle is an idealized thermodynamic cycle and is not appropriate to describe real heat engines such as air standard cycles. The Otto cycle, named after Nikolaus A. Otto, is the ideal cycle for spark-ignition reciprocating engines. The Otto cycle describes the ideal behavior of spark-ignition engines, in which the piston traces four strokes (four-stroke internal combustion engine). The internal combustion engine has intake and exhaust valves. These valves are closed during compression and expansion and they are open while exchanging intake (air mixture) and exhaust (combustion gases).³ The Brayton cycle, named after George Brayton, is used to describe the behavior of the reciprocating oil-burning engine that was developed by Brayton around 1870. The Brayton cycle is used today to describe the behavior of gas turbines which includes four processes: isentropic compression and expansion, and constant pressure heat addition and rejection. The working fluid is ideal gas.³

Stirling and the Ericsson engines are considered external combustion engines. That is, the energy flows to the cylinder from outside. External combustion has some advantages compared to internal combustion. Among these is the flexibility of choosing thermal energy sources, less air pollution due to complete combustion, more efficient use of energy sources, closed cycles operation which enables choosing best working fluids such as Hydrogen and Helium. The Stirling engine includes four processes: isothermal compression, isochoric heat addition, isothermal expansion and isochoric heat rejection. The Ericsson cycle differs from the Stirling cycle by the heat addition and heat rejection processes. While in the Stirling cycle these are isochoric processes, in the Ericsson cycle they are isobaric processes.³ Curzon & Ahlborn⁴ investigated the efficiency of a heat engine at maximum power operation in finite time.^5-10 They considered in 1975 a model of heat engine (usually called the Curzon-Ahlborn engine) with finite heat transfer rates. The heat engine produces zero power output in the extremes of very slow operation and very fast operation. It was found that the heat engine attains a maximum power point with the efficiency at this point being one minus the square root of the ratio between the temperature of the cold reservoir and the temperature of the hot reservoir $\left(n_{CA}=1-\sqrt{\frac{T_L}{T_H}}\right)$ . Bejan¹¹ showed in 1994 that this result of heat engine efficiency at maximum power operation was previously derived by Novikov¹² in 1957 when analyzing the performance of nuclear power plants.

Harvey S Leff¹³ considered four air standard cycles (Otto, Disel, Brayton, Atkinson) and found that the efficiency of these cycles at maximum power operation is similar to the achieved result by Curzon-Ahlborn. The methods of irreversible thermodynamics and finite thermodynamics have been used to analyze thermodynamic systems.^14-32 Analysis of the air standard cycles (Otto and others) could be found elsewhere.^33-60 In this article we ask: what are the effective temperature and the effective efficiency of a heat engine working between two heat reservoirs for the cycles described above? The answers to these questions are given in the following paragraphs. The following sections describe: the SOT function in section II, the model of the heat engine in section III; the Carnot cycle is considered in section IV, the air standard cycles are considered in section V, numerical examples are given in section VI, and finally summary and conclusions are given in section VII.

For a thermal process that goes from state A to state B, the negative integral of the heat transfer change divided by the square of the temperature from state A to state B is given by (a new function introduced in this article and it is called by the author the SOT function):

$SOT=-{\displaystyle \underset{A}{\overset{B}{\int }}\frac{\delta q}{T^2}}$         (1)

For isothermal process the SOT function is given by:

$SOT=-\frac{1}{T^2}{\displaystyle \underset{A}{\overset{B}{\int }}\delta q}$   (2)

The first law of thermodynamics for a process with ideal gas working fluid is given by:

$\delta q=dE+pdV$   (3)

By considering the various process types and using the first law of thermodynamics (eq. 3), makes it easy to write explicit forms of the SOT function. In the following subsections some typical processes are considered.

Constant volume process

For the constant volume process (v=const.), the heat transfer change is proportional to the temperature change (dT) with constant volume heat capacity proportionality factor (c_v). In this case the SOT function is given by:

$SOT=c_v\left(\frac{1}{T_A}-\frac{1}{T_B}\right)$   (4)

Constant pressure process

For the constant pressure process (p=const.), the heat transfer change is proportional to the temperature change (dT) with constant pressure heat capacity proportionality factor (c_p). In this case the SOT function is given by:

$SOT=c_p\left(\frac{1}{T_A}-\frac{1}{T_B}\right)$    (5)

 Constant temperature process

For the constant temperature process (T=const.), the heat transfer change is proportional to the volume change (dv) with pressure proportionality factor (p). In this case the SOT function is given by:

$SOT=\frac{R}{T}\ln \left(\frac{v_A}{v_B}\right)$   (6)

Isentropic process

For the isentropic process-constant entropy process (s=const.), the heat transfer change is zero. In this case the SOT function is given by:

$SOT=0$     (7)

For a heat engine going in a cycle the SOT function is given by:

$SOT=-{\displaystyle \oint \frac{\delta q}{T^2}}$     (8)

Consider a heat engine working between two heat reservoirs, a hot reservoir at high temperature (T_H) and a cold reservoir at low temperature (T_L). The schematics of the heat engine are depicted in Figure 1.

The net work output w_net is calculated by means of the first law of thermodynamics (eq. 3) and is given by:

$w_{net}=Q_H-Q_L$      (9)

The SOT function is given by equation (8).

The effective temperature is defined as the square root of the ratio between the net work output and the SOT function, and is given by:

$w_{net}=Q_H-Q_L$     (10)

Finally, the effective efficiency is defined as the difference between unity minus the ratio between the low temperature and the effective temperature, and is given by:

$n_{eff}=1-\frac{T_L}{T_{eff}}$     (11)

The schematic of the Carnot heat engine is depicted in Figure 1. The net work output is given by (eq. 9). The Carnot cycle includes two processes: heat addition and heat rejection at constant temperatures (high and low) connected with two isentropic (reversible adiabatic) processes. The entropy of the heat engine is calculated by means of the second law of thermodynamics and is given by:

${\displaystyle \oint \frac{\delta q}{T}}=0$    (12)

By applying the assumptions of the Carnot cycle, equation (12) could be written explicitly as follows:

$\frac{Q_H}{T_H}=\frac{Q_L}{T_L}$    (13)

The SOT function for the Carnot cycle is derived by means of equation 1 and is given by:

$\frac{Q_H}{T_H}=\frac{Q_L}{T_L}$    (14)

Applying equation (13) to equation (4) aids to simplify the expression for the SOT function. After algebraic manipulation and using equation (9), the SOT function of the Carnot heat engine simplifies to the following:

$SOT=\frac{w_{net}}{T_L{T}_H}$    (15)

Then, the effective temperature is defined as the geometric mean of the high temperature and the low temperature, a result suggested by (eq. 15) and is given by:

$n_{eff}=\sqrt{T_L{T}_H}=\sqrt{\frac{w_{net}}{SOT}}$   (16)

Finally, the effective efficiency for the Carnot heat engine is given by:

$n_{eff}=1-\frac{T_L}{T_{eff}}=1-\sqrt{\frac{T_L}{T_H}}$     (17)

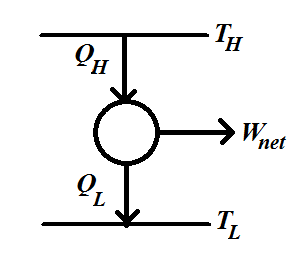
Figure 1 Schematics of the engine working between two heat reservoirs, a hot reservoir at high temperature TH and a cold reservoir at low temperature TL. The heat input to the heat engine is QH and the heat rejection from the heat engine is QL. The net work output wnet is given by the QH-QL.

Ideal Otto cycle

The ideal Otto cycle is used to estimate the efficiency of spark ignition (SI) engine (Otto engine). The schematic of the Pressure–Volume (P-V) diagram of the ideal Otto cycle is shown in Figure 2. The cycle includes four processes: 1à2 isentropic compression, 2à3 constant volume heat addition, 3à4 isentropic expansion, and 4à1 constant volume heat rejection.

For a given initial state (pressure P₁, volume V₁, temperature T₁) with known highest temperature T₃, the application of the thermodynamic state relations and the first law of thermodynamics of the different branches lead to the following results:

The heat input to the engine Q_H is given by:

$Q_H=c_v(T_3-T_2)=c_v{T}_3(1-\tau a)$     (18)

Where c_v is the constant volume heat capacity,  is the ratio between T₁ and T₃ and a () is the compression ratio r raised to the power (k-1) with k equals the ratio between constant pressure heat capacity (c_p) and constant volume heat capacity (k=c_p/c_v).¹

The heat rejection from the engine is given by:

$Q_L=c_v(T_4-T_1)=c_v{T}_3\frac{(1-\tau a)}{a}$    (19)

Where T₄ is the temperature at state 4.

The net work output (w_net) extracted by the engine is given by:

$w_{net}=Q_H-Q_L=c_v{T}_3(1-\tau a)\left(1-\frac{1}{a}\right)$    (20)

The SOT function is calculated based on equation (8). Noting that the contributions of the isentropic branches to the SOT function are zero, the resulting SOT function for the ideal OTTO cycle is given by:

$SO{T}_{Otto}=\frac{c_v}{T_1}(1-\tau a)\left(1-\frac{1}{a}\right)$      (21)

By comparing equations (20) and (21) it is observed that the effective temperature could be deduced and is given by:

$T_{eff}=\sqrt{\frac{w_{net}}{SO{T}_{Otto}}}=\sqrt{T_1{T}_3}$    (22)

The effective efficiency for the ideal OTTO cycle is given by equation (17), where $T_{eff}=\sqrt{\frac{w_{net}}{SO{T}_{Otto}}}=\sqrt{T_1{T}_3}$ is replaced by $T_L$ and $T_3$ is replaced by $T_H$ .

Ideal Brayton cycle

The ideal Brayton cycle is used to estimate the efficiency of gas turbines. The schematic of the Pressure–Volume (P-V) diagram of the ideal Brayton cycle is shown in Figure 3. The Brayton cycle includes four processes: 1à2 isentropic compression, 2à3 constant pressure heat addition, 3à4 isentropic expansion, and 4à1 constant pressure heat rejection.

For a given initial state (pressure P₁, volume V₁, temperature T₁) with known highest temperature T₃, the application of the thermodynamic state relations and the first law of thermodynamics of the different branches lead to the following results:

The heat input to the engine Q_H is given by:

$T_H$   (23)

Where c_p is the constant pressure heat capacity,$\tau$ is the ratio between T₁ and T₃ and a ($a=r^{k-1}$ ) is the compression ratio r raised to the power (k-1) with k equals the ratio between constant pressure heat capacity (c_p) and constant volume heat capacity (k=c_p/c_v).

The heat rejection from the Brayton cycle is given by:

$Q_L=c_p(T_4-T_1)=c_p{T}_3\frac{(1-\tau a)}{a}$   (24)

Where T₄ is the temperature at state 4.

The net work output (w_net) extracted by the Brayton cycle is given by:

$w_{net}=Q_H-Q_L=c_p{T}_3(1-\tau a)\left(1-\frac{1}{a}\right)$    (25)

The SOT function is calculated based on equation (8). Noting that the contributions of the isentropic branches to the SOT function are zero, the resulting SOT function for the ideal Brayton cycle is given by:

$SO{T}_{Brayton}=\frac{c_p}{T_1}(1-\tau a)\left(1-\frac{1}{a}\right)$     (26)

By comparing equations (25) and (26) it is observed that the effective temperature could be deduced and is given by:

$T_{eff}=\sqrt{\frac{w_{net}}{SO{T}_{Brayton}}}=\sqrt{T_1{T}_3}$    (27)

The effective efficiency the ideal Brayton cycle is given by equation (17), where $T_1$ is replaced by $T_L$ and $T_3$ is replaced by $T_H$ .

Ideal Stirling cycle

The ideal Stirling cycle is used to estimate the efficiency of Stirling engine. The schematic of the Pressure–Volume (P-V) diagram of the ideal Stirling cycle is shown in Figure 4. The cycle includes four processes: 1à2 isothermal compression, 2à3 constant volume heat addition, 3à4 isothermal expansion, and 4à1 constant volume heat rejection.

For a given initial state (pressure P₁, volume V₁, temperature T₁) with known highest temperature T₃, the application of the thermodynamic state relations and the first law of thermodynamics of the different branches lead to the following results:

The heat input to the Stirling cycle Q_H is given by:

$Q_H=c_v(T_3-T_2)+R{T}_3\ln (r)$    (28)

Where c_v is the constant volume heat capacity,$\tau$ is the ratio between T₁ and T₃ and a ($a=r^{k-1}$ ) is the compression ratio r raised to the power (k-1) with k equals the ratio between constant pressure heat capacity (c_p) and constant volume heat capacity (k=c_p/c_v).

The heat rejection from the Stirling cycle is given by:

$Q_L=c_v(T_4-T_1)+R{T}_1\ln (r)$    (29)

Where T₄ is the temperature at state 4 and R is the ideal gas constant.

The net work output (w_net) extracted by the Stirling cycle is given by:

$w_{net}=Q_H-Q_L=c_{v}R{T}_3(1-\tau )\ln (r)$     (30)

The SOT function is calculated based on equation (8). Noting that the contributions of the isothermal branches to the SOT function cancel each other, the resulting SOT function for the ideal Stirling cycle is given by:

$SO{T}_{Stirling}=R\ln (r)\left(\frac{1}{T_1}-\frac{1}{T_3}\right)=\frac{R\ln (r)}{T_1}\left(1-\tau \right)$    (31)

By comparing equations (30) and (31) it is observed that the effective temperature could be deduced and is given by:

$T_{eff}=\sqrt{\frac{w_{net}}{SO{T}_{Stirling}}}=\sqrt{T_1{T}_3}$     (32)

The effective efficiency the ideal OTTO cycle is given by equation (17), where is replaced by  and  is replaced by.

Ideal Ericsson cycle

The ideal Ericsson cycle is used to estimate the efficiency of the Ericsson engine. The schematics of the Pressure–Volume (P-V) diagram of the ideal Ericsson cycle is shown in Figure 5. The cycle includes four processes: 1à2 isothermal compression, 2à3 constant pressure heat addition, 3à4 isothermal expansion, and 4à1 constant pressure heat rejection.

For a given initial state (pressure P₁, volume V₁, temperature T₁) with known highest temperature T₃, the application of the thermodynamic state relations and the first law of thermodynamics of the different branches lead to the following results:

The heat input to the engine Q_H is given by:

$Q_H=c_p(T_3-T_2)+R{T}_3\ln (r)$   (33)

Where c_v is the constant volume heat capacity,$\tau$ is the ratio between T₁ and T₃ and a ($a=r^{k-1}$ ) is the compression ratio r raised to the power (k-1) with k equals the ratio between constant pressure heat capacity (c_p) and constant volume heat capacity (k=c_p/c_v).

The heat rejection from the engine is given by:

$Q_L=c_p(T_4-T_1)+R{T}_1\ln (r)$      (34)

Where T₄ is the temperature at state 4.

The net work output (w_net) extracted by the engine is given by:

$w_{net}=Q_H-Q_L=R{T}_3(1-\tau )\ln (r)$    (35)

The SOT function is calculated based on equation (8). Noting that the contributions of the isobaric branches to the SOT function cancel each other, the resulting SOT function for the ideal Ericsson cycle is given by:

$SO{T}_{Ericsson}=R\ln (r)\left(\frac{1}{T_1}-\frac{1}{T_3}\right)=\frac{R\ln (r)}{T_1}\left(1-\tau \right)$   (36)

By comparing equations (35) and (36) it is observed that the effective temperature could be deduced and is given by:

$T_{eff}=\sqrt{\frac{w_{net}}{SO{T}_{Ericsson}}}=\sqrt{T_1{T}_3}$    (37)

The effective efficiency the ideal OTTO cycle is given by equation (17). where $T_1$ is replaced by $T_L$ and $T_3$ is replaced by $T_H$ .

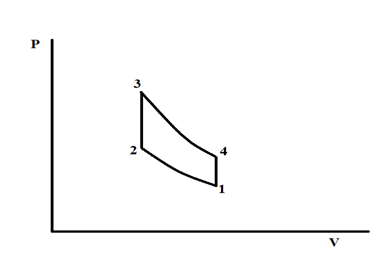
Figure 2 Schematics if the ideal Otto cycle.

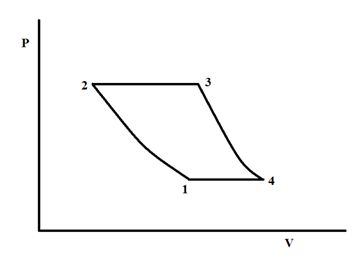
Figure 3 Schematics if the ideal Brayton cycle.

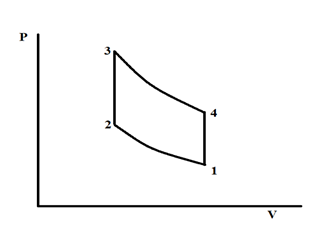
Figure 4 Schematics if the ideal Stirling cycle.

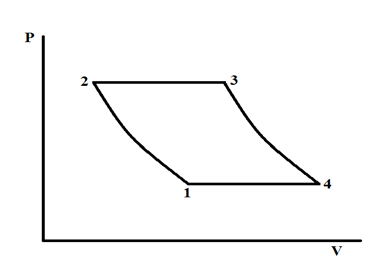
Figure 5 Schematics if the ideal Ericsson cycle.

The following table compares the effective efficiency with Carnot efficiency and with the observed efficiency for some real plants. As can be seen, the effective efficiency is much closer to the observed data.⁶⁰

For a heat engine working between two heat reservoirs, a hot reservoir at high temperature T_H and a cold reservoir at a low temperature T_L the Carnot cycle and Curzon-Ahlborn heat engine were shortly reviewed and their performance efficiencies are given via the Carnot efficiency and the Curzon-Ahlborn respectively. The new terms SOT function, effective temperature and the effective efficiency were introduced. The SOT function was defined as minus the cyclic integral of the heat change divided by the temperature squared. The effective temperature was defined as the square root of the ratio between the net work output and the SOT function, and finally the effective efficiency was defined as one minus the ratio between the cold reservoir temperature and the effective temperature. The SOT function was calculated for different thermodynamic processes: isochoric, isobaric, isothermal and isentropic. A model of heat engine was considered and general expressions of the SOT function, effective temperature and effective efficiency were given as useful tools for the designer. These expressions were applied to different thermodynamic cycles: The Carnot cycle and air standard cycles (Otto, Brayton, Stirling and Ericsson). The effective temperature for the considered heat engines was given as the square root of the product of the reservoirs' temperatures and the efficiency was given as one minus the square root of the ratio between the cold reservoir temperature and the hot reservoir temperature. The derived expressions can serve two important purposes: in education and for a quick estimation tool for heat engine designers.

The author declares that there is no conflict of interest regarding the publication of this paper.

1. Sonntag RE, Van Wylen GJ. Introduction to Thermodynamics. 3rd ed. New York: Wiley; 1991. 800 p.
2. Callen HB. Thermodynamics and an Introduction to Thermostatics. 2nd ed. New York: Wiley; 1985. 493 p.
3. Cengel YA, Boles MA. Thermodynamics: An Engineering Approach. 5th ed. Boston: McGraw-Hill College; 2006.
4. Curzon FL, Ahlborn B. Efficiency of a Carnot Engine at Maximum Power Output. Am J Phys. 1975;43(1):22.
5. Chen LG, Wu C, Sun FR. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J Non-Equilib Thermodyn. 1999;24(4):327–359.
6. Wu C, Chen LG, Chen JC. Recent Advances in Finite Time Thermodynamics. New York: Nova, Science Publishers; 1999. 560 p.
7. Chen LG, Sun FR. Advances in Finite Time Thermodynamics: Analysis and Optimization. New York: Nova Science Publishers; 2004. 240 p.
8. Chen LG, Meng FK, Sun FR. Thermodynamic analyses and optimizations for thermoelectric devices: the state of the arts. Science China: Technological Sciences. 2016;59(3):442–455.
9. Ge YL, Chen LG, Sun FR. Progress in finite time thermodynamic studies for internal combustionengine cycles. Entropy. 2016;18(4):139.
10. Chen LG, Feng HJ, Xie ZH. Generalized thermodynamic optimization for iron and steel production processes: Theoretical exploration and application cases. Entropy. 2016;18(10):353.
11. Bejan A. Engineering Advances in Finite-Time Thermodynamics. Am J Phys. 1994;62(1):11–12.
12. Novikov II. The efficiency of Atomic Power Stations. J Nucl Energy II. 1958;7:125–128.
13. Harvey S Leff. Thermal efficiency at maximum work output: New results for old heat engines. Am J Phys. 1987;55(7):602-610.
14. Andresen B, Salamon P, Berry RS. Thermodynamics in finite time. Physics Today. 1984;37(9):62–70.
15. Andresen B, Salamon P, Berry RS. Thermodynamics in finite time: extremals for imperfect heat engines. The Journal of Chemical Physics. 1976;66(4):1571–1576.
16. Salamon P, Nitzan A, Andresen B, et al. Minimum entropy production and the optimization of heat engines. Phys Rev. 1980;21(6):2115–2129.
17. Salamon P, Berry RS. Thermodynamic length and dissipated availability. Phys Rev Lett. 1983;51(13):1127–1130.
18. Rubin MH. Optimal configuration of a class of irreversible heat engines I. Phys Rev A. 1979;19(3):1272–1276.
19. Salamon P, Band YB, Kafri O. Maximum power from a cycling working fluid. Journal of Applied Physics. 1982;53(1):197–202.
20. Mozurkewich M, Berry RS. Optimal paths for thermodynamic systems: the ideal Otto cycle. Journal of Applied Physics. 1982;53(1):34–42.
21. Gordon JM, Huleihil M. On optimizing maximum power heat engines. Journal of Applied Physics. 1991;69(1):1–7.
22. Gordon JM, Huleihil M. General performance characteristics of real heat engines. Journal of Applied Physics. 1992;72(3):829–837.
23. Nulton JD, Salamon P, Pathria RK. Carnot-like processes in finite time. I. Theoretical limits. Am J Phys. 1993;61(10):911–916.
24. Nulton JD, Salamon P, Pathria RK. Carnot-like processes in finite time. II. Applications to model cycles. Am J Phys. 1993;61(10):916–924.
25. Chen J, Yan Z. Optimal performance of an endoreversible combined refrigeration cycle. Journal of Applied Physics. 1988;63(10):4795–4798.
26. Bejan A. Theory of heat transfer-irreversible refrigeration plants. International Journal of Heat and Mass Transfer. 1989;32(9):1631–1639.
27. Chen J, Yan Z. Equivalent combined systems of threeheat-source heat pumps. The Journal of Chemical Physics. 1989;90(9):4951–4955.
28. Chen J, Yan Z. An optimal endoreversible three-heatsource refrigerator. Journal of Applied Physics. 1989;65(1):1–4.
29. Gordon JM, Ng KC. Thermodynamic modeling of reciprocating chillers. Journal of Applied Physics. 1994;75(6):2769–2774.
30. Bhardwaj PK, Kaushik SC, Jain S. Finite time optimization of an endoreversible and irreversible vapour absorption refrigeration system. Energy Conversion and Management. 2003;44(7):1131–1144.
31. Bi Y, Chen L, Sun F. Exergetic efficiency optimization for an irreversible heat pump working on reversed Brayton cycle. Pramana. 2010;74(3):351–363.
32. Bhardwaj PK, Kaushik SC, Jain S. General performance characteristics of an irreversible vapour absorption refrigeration system using finite time thermodynamic approach. International Journal of Thermal Sciences. 2005;44(2):189–196.
33. Hou SS. Comparison of performances of air standard Atkinson and Otto cycles with heat transfer considerations. Energy Conversion and Management. 2007;48(5):1683–1690.
34. Chen L, Zheng T, Sun F, et al. The power and efficiency characteristics for an irreversible Otto cycle. International Journal of Ambient Energy. 2003;24(4):195–200.
35. Chen J, Zhao Y, He J. Optimization criteria for the important parameters of an irreversible Otto heat-engine. Applied Energy. 2006;83(3):228–238.
36. Zhao YR, Chen JC. Irreversible Otto heat engine with friction and heat leak losses and its parametric optimum criteria. Journal of the Energy Institute. 2008;81(1):54–58.
37. Feidt M. Optimal thermodynamics-New Upper bounds. Entropy. 2009;11(4):529–547.
38. Ebrahimi R. Effects of gasoline-air equivalence ratio on performance of an Otto engine. J Am Sci. 2010;6(2):131–135.
39. Ebrahimi R. Theoretical study of combustion efficiency in an Otto engine. J Am Sci. 2010;6(2):113–116.
40. Ozsoysal OA. Effects of combustion efficiency on an Otto cycle. International Journal of Exergy. 2010;7(2):232–242.
41. Ebrahimi R, Ghanbarian D, Tadayon MR. Performance of an Otto engine with volumetric efficiency. J Am Sci. 2010;6(3):27–31.
42. Gumus M, Atmaca M, Yilmaz T. Efficiency of an Otto engine under alternative power optimizations. International Journal of Energy and Research. 2009;33(8):745–752.
43. Upper Y. Ecological performance analysis of irreversible Otto cycle. J Eng Natural Sci. 2005;23(3):106–117.
44. Mehta HB, Bharti OS. Performance analysis of an irreversible Otto cycle using finite time thermodynamics. London: Proceedings of the World Congress on Engineering; 2009. 5 p.
45. Wu F, Chen L, Sun F, et al. Quantum degeneracy effect on performance of irreversible Otto cycle with deal Bose gas. Energy Conversion and Management. 2006;47(18-19):3008–3018.
46. Wang H, Liu S, He J. Performance analysis and parametric optimum criteria of a quantum Otto heat engine with heat transfer effects. Applied Thermal Engineering. 2009;29(4):706–711.
47. Wang H, Liu S, Du J. Performance analysis and parametric optimum criteria of a regeneration Bose-Otto engine. Phys Scr. 2009;79(5):055004.
48. Nie W, Liao Q, Zhang C, et al. Micro-/nanoscaled irreversible Otto engine cycle with friction loss and boundary effects and its performance characteristics. Energy. 2010;35(12):4658–4662.
49. Wu F, Chen L, Sun F, et al. Ecological optimization performance of an irreversible quantum Otto cycle working with an ideal Fermi gas. Open System & Information Dynamics. 2006;13(1):55–66.
50. Rocha-Martinez JA, Navarrete-Gonzalez TD, Pava-Miller CG, et al. Otto and Diesel engine models with cyclic variability. Revista mexicana de física. 2002;48(3):228–234.
51. Rocha-Martinez JA, Navarrete-Gonzalez TD, Pava-Miller CG, et al. A simplified irreversible Otto engine model with fluctuations in the combustion heat. International Journal of Ambient Energy. 2006;27(4):181–192.
52. Ge Y, Chen L, Sun F, et al. Thermodynamic simulation of performance of an Otto cycle with heat transfer and variable specific heats of working fluid. International Journal of Thermal Science. 2005;44(5):506–511.
53. Ge Y, Chen L, Sun F, et al. The effects of variable specific heats of working fluid on the performance of an irreversible Otto cycle. International Journal of Exergy. 2005;2:274–283.
54. Zhao Y, Lin B, Chen J. Optimum criteria on the important parameters of an irreversible Otto heat engine with the temperature-dependent heat capacities of the working fluid. ASME Trans J Energy Res Tech. 2007;129(4):348–354.
55. Lin JC, Hou SS. Effects of heat loss as percentage of fuel’s energy, friction and variable specific heats of working fluid on performance of air standard Otto cycle. Energy Conversion and Management. 2008;49(5):1218–1227.
56. Nejad RM, Marghmaleki IS, Hoseini R, et al. Effects of irreversible different parameters on performance of air standard Otto cycle. J Am Sci. 2011;7:248–254.
57. Ge Y, Chen L, Sun F. Finite time thermodynamic modeling and analysis for an irreversible Otto cycle. Applied Energy. 2008;85(7):618–624.
58. Ebrahimi R. Effects of variable specific heat ratio on performance of an endoreversible Otto cycle. Acta Physica Polonica A. 2010;117(6):887–891.
59. Ebrahimi R. Engine speed effects on the characteristic performance of Otto engines. J Am Sci. 2010;6(1):123–128.
60. Hoffmann KH. Recent developments in finite time thermodynamics. Technische Mechanik. 2002;22(1):14–20.