eISSN: 2576-4500


Research Article Volume 2 Issue 4
Mechanical and Aerospace Engineering, North Carolina State University, USA
Correspondence: Raisa Rose Boben, Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC 27605-7910, USA
Received: June 13, 2018 | Published: August 21, 2018
Citation: Boben RR, Ramnath V, Lyons KM. Effect of moderate-strength magnetic field on local temperature in diffusion flames. Aeron Aero Open Access J. 2018;2(4):250-257. DOI: 10.15406/aaoaj.2018.02.00057
The behavior of laminar jet propane diffusion flames in the presence of moderate-strength permanent magnets has been investigated and the results of this experimental study are presented. While there are many ways of impacting combustion behavior, the impact of magnetic fields and their gradients has, to date, been underexplored. It has been previously recognized that the gradient magnetic field can influence laminar diffusion flames because of paramagnetic and diamagnetic components of the reaction zone of the flame. Using a magnet assembly of moderate-strength neodymium iron boron magnets mounted on an iron yoke, a non-uniform magnetic field was applied to the laminar jet flame. Propane/air flames with different flow velocities were produced from a 0.81mm burner port and the reaction zone was subjected to a gradient magnetic field. The experimental results show that the reaction zone exhibited a significant increase in local temperature under the influence of a decreasing magnetic gradient field. Compared with the case of the zero-magnetic field applied, the flame temperature increased by an average of 40K. In an increasing magnetic gradient field, the local temperature is expected to decrease, but it was found to increase slightly relative to the zero-magnetic field case. It was still found to be lower than the decreasing magnetic gradient field condition. It appears that the impact of the magnetic field is not strongly dependent on the burner tip position in the magnetic field gradient.
The energy associated with the magnetic influence on flame behavior is generally several orders of magnitude smaller than the kinetic energy of molecules at room temperature. Nevertheless, recent studies have shown that an inhomogeneous magnetic field provides a means to control combustion behavior. Gaseous combustion comprises of not only a chemical reaction but also of physical processes of heat transfer and mass diffusion. These processes can be manipulated using magnetic forces applied on paramagnetic gas flows to the flame. The motivation for this study is to look at the effects produced by a magnetic field of moderate-strength. The benefits of using permanent magnets include negating the need for external energy sources to produce high magnetic field strengths, as well as relatively less expensive. Magnetic fields are known to affect flame behavior and gas flows because of the paramagnetic and diamagnetic nature of the constituent gases. Paramagnetism is a form of magnetism whereby certain materials are weakly attracted by an externally applied magnetic field, and form internal, induced magnetic fields in the direction of the applied magnetic field. Paramagnetic materials include aluminum, oxygen, titanium, and iron oxide. In contrast with this behavior, diamagnetic materials are repelled by magnetic fields and form induced magnetic fields in the direction opposite to that of the applied magnetic field. Nitrogen, CO2, and most hydrocarbon fuels are examples of diamagnetic materials and experience a weak repulsion to the applied magnetic field.
The magnetic susceptibility, the ratio of the magnetization to the magnetic field strength,1 is the parameter that characterizes this behavior. All materials, to some degree, display diamagnetic behavior. For materials whose atoms possess permanent dipole moments, the associated paramagnetic forces are typically orders of magnitude larger and the diamagnetic behavior for these materials is thus negligible.2 The magnetic susceptibility for a diamagnetic material is not a strong function of temperature and is negative in sign while a paramagnetic material has a positive magnetic susceptibility. A diffusion flame is used as a test subject to study the effect of the magnetic field since it simulates combustion characteristics found in various industrial applications. A diffusion flame is a flame in which fuel and oxidizer come together in a reaction zone through molecular and turbulent diffusion. The fuel may be in the form of a condensed medium (either solid or liquid) or in the gaseous form of a gaseous fuel jet, and the oxidizer may be a flowing gas stream or the quiescent atmosphere. It is the diffusion rate of the fresh mixture into the flame zone which sustains combustion and hence the name.
In diffusion flames, hydrocarbon fuels, nitrogen, carbon dioxide are diamagnetic; oxygen is the principal paramagnetic gas. As the paramagnetic susceptibility of oxygen is orders of magnitude larger, the diamagnetic behavior is considered as negligible. A gas containing more O2, such as air, tends to move towards the stronger magnetic field and a gas with less O2 such as fuel or combustion gas tends to move towards the weaker magnetic field. Based on this, it may be possible to utilize a magnetic field to control the flow field of the combustion region to improve combustion characteristics. A key parameter to characterize the laminar diffusion flame behavior is the flame height under the influence of the magnetic field.3 The flame height (Lf) is defined as the vertical distance between the burner surface and the point along the flame axis where the fuel is consumed in stoichiometric proportions.4 At present, magnetic control of combustion and gas flow with low-cost permanent magnets is a relatively new scope of research and further experimental study is required to establish the mechanism for this interaction. The specific objective of the study is to design an experimental set-up to measure a local representative temperature. In addition, the influence of magnetic forces to promote combustion compared to the normal buoyancy forces induced by gravity in diffusion flames is studied.
A large assembly of research has recently been carried out to study the effects of magnetic field on the behavior of flames to understand its mechanism. The effect was first recognized in 1847 when Michael Faraday5 held a flame of a wax taper with the magnetic field and observed its tendency to move into an equatorial position. He also observed that the flames were more luminous when placed with the magnetic field. He theorized that the changes were due to the presence of “magnetic” and “diamagnetic” gases in the flames. Over the past 30 years, there has been a renewed interest in the impact of magnetic field on combustion behavior. Hayashi6 investigated magnetic field effects on the emission intensities of intermediate species in premixed flames. He found that the magnetic field is seen to increase the combustion efficiency through the increase in the population of OH* radicals. He thought that this change in the combustion process is due to the magnetically induced change of singlet-triplet conversion rate.7 Aoki8 rejected this theory for the gaseous combustion process since, in a gaseous phase, the lifetimes of a radical pair disappear before inverting the spins of excited states by S-T conversions.
Ueno S & Harada K9 investigated this behavior on candle flames. They noted that the presence of an increasing magnetic field gradient caused the flame to deflect in the direction of decreasing magnetic field strength. They came up with two reasons for this behavior; first, the charged particles in flame plasma made a current loop that tended to reduce the external magnetic field. Thus, flames escape from the magnetic field of higher intensity. Second, paramagnetic O2 gases could be gathered by a magnetic field gradient and create a magnetically induced pressure to press back other diamagnetic gases and particles. To clarify this behavior, Ueno S & Harada K10,11 expanded their research to study flames and jets of gas flow. Since the gas flow was also impacted by the magnetic field, the first hypothesis of charged particle theory was rejected. He also concluded that the presence of a strong magnetic gradient did not concentrate oxygen but aligned or trapped the molecules to make a “wall of oxygen” under the influence of magnetic gradients like an “air curtain” that pressed back flames and other gases. In 1990, Ueno S & Iwasaka M11 studied the properties of air curtain and observed that the flow of CO2 gas wasn’t blocked by the magnetic field in the N2 atmosphere, which emphasizes the importance of O2 as a paramagnetic gas in the formation of a magnetic curtain.
Aoki8 was the first one to investigate the effect of an inhomogeneous magnetic field under increasing, decreasing and uniform magnetic field gradients. In case of an upward decreasing field generated by electromagnets, he found that the presence of a magnetic field caused an increase in the flame temperature, emission intensities of radicals OH*, CH8 and C2* transitions and a bluing tendency of the flames. The author used a simplified diffusion model to explain the increase in flame temperature and flame dimensions in a diffusion flame; that they were mainly because of the effect of magnetic force. This magnetic force acting on the paramagnetic species changes the gas flow which affects the mixing and diffusion process conditions. Therefore, it is the changes in the actual physical processes that change the combustion state and not the chemical reaction itself.
On the other hand, the upward-increasing magnetic fields12 increased the flame dimensions; they decreased radical emissions, temperatures and the bluing tendency. These phenomena were contrary to those observed in previous studies. He also investigated butane combustion under a uniform magnetic field encircled by a magnetic field.13 He observed no effect on combustion state, except for some changes that can be ascribed to the magnetic gradient produced by pole fringes. This exists for most of the magnets and is unavoidable. He showed that the velocities of electrons and ions produced by the combustion reaction are very low in the diffusive flame where the flow is dominated by buoyant force. Hence, the effect of Lorentz forces on the deformation of the flame was insufficient to cause any appreciable changes in flame within the magnetic field. Yamada14 supported this, as the amount of ionic species is negligibly small, and the influence of the Lorentz force can be ignored in ordinary flames. This explanation of magnetic force theory was also supported by Wakayama15 when she conducted experiments on O2, N2, a mixture of the two and air. The behavior of gas flow can be explained by the difference between the magnetic force acting on the gas group and the air surrounding it.
She explained that the air was attracted to the magnetic field which displaced the nitrogen gas from a magnetic field of relatively high intensity. This explanation also applies to the escape of flames from a high magnetic field gradient or magnetic quenching of flames observed by Ueno11. Thus, the study demonstrates that it is the magnetic susceptibility of gas groups which exerts a net magnetic force that blocks the gas flow. Later, Wakayama16,17 studied premixed, partially-premixed and diffusion methane flames within the magnetic field gradients. The results of these experiments brought to light a distinct thought process for the interaction of flames with magnetic fields. It was observed that a decreasing magnetic field along the flame caused its shape to be more elongated and slender, while an increasing magnetic field produced shorter and thicker flames. It was also observed that the temperature and luminosity of the flame increased with increasing gradient strength. These observations were attributed to the paramagnetic nature of oxygen and the diamagnetic properties of the products of combustion. She suggested two reasons for the magnetic promotion of combustion in diffusion flames. First, when fuel gas flows in the direction of decreasing field strength, the paramagnetic nature of oxygen increases the diffusion rate of air to the reaction zone and diamagnetic reaction products reject out efficiently. Accordingly, the burning velocity increases with increasing strength. Secondly, magnetic convection of air is also magnetically promoted because the gradient of temperatures causes the gradient of magnetic susceptibilities. The latter effect is less than the former one, comparing the difference of the magnetic susceptibilities in both cases.
However, no significant changes were observed for partially premixed flames and no effects on premixed flames, in either increasing or decreasing magnetic fields. Also, when the flames were moved to a homogenous field, the flames did not appear to be affected. Again in 2000, Mizutani18 found that premixed flames were hardly affected by a uniform magnetic field as intense as 5T. He also concluded that the direct effects of the magnetic field on the chemical kinetics of flame propagations are negligible. This suggested the convection of oxygen into the regions of increasing strength was the most dominant factor in affecting the combustion behavior. Hence, a diffusion flame is best suited to study the effect of a non-uniform magnetic field, as this combustion reaction occurs in the interface where the oxidizer and air react in stoichiometric proportions.
Diffusion flames are mainly governed by physical processes of mixing and diffusion of fuel gas and oxidizer. The rate of combustion is altered by magnetic field modifying the transport phenomena of oxidizer (Figure 1) to the reaction zones of such flames. Wakayama & Sugie19 suggested two kinds of air flow that promoted combustion in methane diffusion flames within 2cm gap of electromagnets. Air was magnetically attracted along the steepest gradient (solid lines) and supplied to the flame front. This makes flame front velocity three orders larger than the diffusion rate by natural physical processes. Furthermore, magnetic convective air flow occurred along the y-axis (dotted lines) feeding oxidizer to the leading edge of the flame because magnetic susceptibility of air is proportional to. Accordingly, the direction of magnetic force in decreasing magnetic field facilitates this combined movement of involved species to promote combustion in diffusion flames.
Yamada et al.,14 performed a numerical analysis of OH radical distributions in H2/O2 diffusion flames. It was observed that the magnetic gradient induced changes in the repartition of OH density in the flame. The effect is due to the enhancement of the entrainment gas flow around the flame base. This increases the mass density and then the magnetic susceptibility of oxygen in the peripheral region of the flame. To explore the possibility of combustion control by magnetic force, they20 performed experiments using a co-axial type burner set between permanent magnets. Using spectroscopic techniques, they measured radial migration of OH towards the central axis of the flame as predicted numerically. Numerical simulations based on gas dynamics and magnetism showed that the magnetic force acts on the mean velocity of the gas mixture and not on the diffusion velocity of OH radicals. Hence, the magnetic effect is essentially due to magnetic force acting on O2 and not directly on OH itself.
Baker et al.,21 studied the characteristics of slotted laminar jet diffusion flames in the presence of upward decreasing magnetic field produced by permanent magnets. The magnetic field decreased the flame height, increased the intensity of the flame, reduced the flow rate for which visible soot inception occurred, and increased the flow rate below which the flame extinguished. They provided a power-law fit between the experimental data and dimensionless parameters, which shows an inverse relation between magnetic body force and flame height. Khaldi22 investigated the phenomenon of thermos-magnetic convection due to the dependence of the O2 magnetic susceptibility on temperature. They redefined the Rayleigh number as the results showed that heat transfer driven by magneto-gravity buoyancy is like that driven by gravity alone. Gillon23 did extensive research on lift-off height of methane co-flow diffusion flames. Flame lift-off is referred to as the phenomenon in which the fuel mass flow rate exceeds a critical value and the flame and burner become separated. When the mass flow rate increases further, the lift-off height increases until the flame becomes flat and then blows out. The flame is said to be stabilized where the flame propagation speed with respect to the fuel/oxidizer matches the local flow velocity. Under the influence of an upward decreasing magnetic field, Gilard24 observed a reduction in lift-off height. Magnetic force acting downwards on paramagnetic oxygen molecules decreases the air velocity locally. This modification of the external air mixing layer enhances the radial diffusion of methane and drops the stoichiometric line moving the flame front to a lower position. Kumar25 & Aggarwal et al.,26 studied the effect of magnetic field on the temperature profile of butane diffusion flame. The maximum flame temperature increased under an upward-decreasing magnetic gradient and decreased under an upward-increasing magnetic gradient, while a negligible effect on temperature was noted in a uniform magnetic field.
The experimental device is installed at the Reacting Flow and Turbulent Jets laboratory in the MAE department of NC State University. The components are designed and fabricated in a way to produce a laminar propane/air diffusion flame which is convenient for accurate temperature measurements. The experiments were carried out in the presence of a magnetic gradient field created by a permanent magnet placed around the burner system and the results are compared to a case of zero-magnetic field created using false magnets. All the components were made using non-magnetic materials to avoid any unwarranted attractions by the application of the magnetic field on the setup used. A picture of the experimental setup is shown in Figure 2 with the pertinent elements identified. The experimental setup is placed where the surrounding air remains relatively static, is mainly composed of the propane-air diffusion burner, yoke with the magnets, flow meter along with provisions for local temperature measurements.
The burner system is required to produce laminar flow conditions for the fuel gas issuing into the ambient air and to maintain a stable flame environment for temperature measurement required for this system. The fuel flow rate was regulated using a metering valve to ensure accurate results reproducible over multiple tests under similar conditions. A schematic representation of the burner is shown in Figure 3. The burner consists of a cylindrical base set on a stand through which a series of PVC fittings have been configured.
The burner setup consists of a fuel supply system and the diffusion burner. Propane gas was fed into the inner tube of 0.81mm inner diameter is selected for this investigation. Due to a burner length of 125mm, the gas flow is assumed to be fully developed at the exit of the burner, with a Poiseuille-type velocity distribution. The main purpose of the fuel supply system is to supply the combustion gases to the burner in controlled proportions. This supply system consists of compressed gas cylinders, flow meters, valves, and tubing, and can supply the fuel gases, oxidizer and others such as purge gases, both to a premixed and a diffusion burner configuration, present in the lab. The line supplying gases issues 99.0% pure CP grade propane (C3H8) was supplied from the cylinder to the diffusion burner. It flows through a Yor-Lok precision flow adjustment needle valve to govern the passage of the fuel gases and was monitored using volumetric flow meter (OMEGA, FMA-A2309) having a range of 0-10SLPM. The readings were estimated to be accurate within 5%. This range is sufficient for experiments to be performed over a wide range of jet velocities. Propane is injected at ambient temperature (i.e. 292.7K).
In this investigation, N52 grade permanent magnets (DX8C-N52) having a diameter of 37.6mm and a depth of 19.05mm is used to generate the gradient magnetic field. Two magnets, each of which could produce a pull force of 52.3Kg towards a steel plate are used in the current investigation. Placing two of these magnets in an iron yoke completes a path for the magnetic flux which enables a magnetic field whose strength is stronger than the individual strength of the magnets, to be formed between the poles of the magnet. Plain Iron Yoke design was selected based on a prior study done by Vikram27 in the lab. This design is selected for its combination of a sufficiently high field and a reasonably big air gap and is fabricated. The yoke with the magnets is shown in Figure 4.
The magnetic field induction was measured along the vertical z-axis position using a Gauss meter with a transverse probe where the uncertainty of measurement was 1% and is shown in Figure 5. The influence of the magnetic field along the flame length is studied and hence the field distribution in the vertical direction is emphasized. Figure 5 also shows the specific locations of study employed in this experiment. The burner nose is positioned to be in two vertical positions A and B so that the flame experiences an increasing gradient magnetic field when the burner is set at position A and a decreasing gradient magnetic field when it is set at position B. The measurements of these cases were compared to a case of the zero-magnetic field.
Temperature measurements
The most critical element to this study is to identify the effect of non-uniform magnetic fields on the combustion processes occurring in the diffusion flame. The local temperature was monitored with a high-temperature Type K thermocouple probe, enclosed in a protection tube. Type K thermocouple has been chosen since it can accommodate temperatures up to 1523K. The temperature is measured at the highest point on flame tip along the z-axis for a given configuration. The thermocouple translation mechanism facilitates this movement for the different axial positions of flame tip for a given flow velocity as shown in Figure 1. The thermocouple is connected to the digital temperature reader (CL3515R), which is a portable thermometer with a 4-digit LCD. It is designed to be used with an external K Type thermocouple as temperature sensors. It has an accuracy of ± (0.05% rdg+0.5 K) -223 to 1645K. It includes DAQ (Data Acquisition) software to record the measurements and export the data in excel format.
Temperature correction for radiation losses
In a high-temperature environment, such as the hot-flame gases in the current burner arrangement, one major source of uncertainty in the measurement of local temperature is the correction for radiation. The temperature read by the thermocouple is less than the true value due to radiation heat transfer between the thermocouple surface and the surroundings. Under the assumption of steady-state temperature, an energy balance around the thermocouple bead may be written as the sum of conductive, convective, radiative and catalytic heat gain/loss:
where mb and cp, b are the bead mass and the bead specific heat, respectively. Catalytic effects may be neglected a priori due to the choice of a K-type chromel/alumel thermocouple, whose materials can be considered non-reactive under the present conditions. Neglecting the conduction through thermocouple wires, the convective heat transfer between the thermocouple and the flame gases should be equal to net radiative heat exchange between the thermocouple bead and its ambient surroundings. Thus, the radiation correction has been considered. If Tm, the thermocouple temperature is the same through the thermocouple probe and that steady condition prevails, the derivation for the temperature correction is as shown below:
Where; Tf is the corrected local temperature (K), Tm is the measured temperature (K), by equating the above two equations the corrected temperatures were calculated by using the relation:
The value of the convective heat transfer coefficient hg is approximated using the Nusselt number definition for a sphere immersed in a fluid28 and given by the equations:
This equation for hg is valid for the case of forced convection from a sphere for Reynolds number in the range 1-70,000.28
A set of experiments were carried out to determine the temperature distribution as a function of propane flow velocity within the flame. A propane/air diffusion flame was established for various fuel flow rates and the measured local temperatures were corrected for radiation losses. The measurements were carried out for three different cases; increasing magnetic field gradient, decreasing magnetic field gradient and when no magnetic field was applied. The temperatures were measured at the flame tip for each of the above cases. This represents the peak local temperature value along the central axis of the flame length. The thermocouple was positioned along the flames’ central axis and gradually positioned at the flame tip on the z-axis. For a circular port flame, the flame length does not depend on diameter but, rather, on the initial volumetric flow rate29 so, the propane flow rate is varied to produce a flame whose height is within the influence of the magnetic field. This limited the maximum flow velocity for the experiments to 0.051m/s. The local temperature test values represent the average of ten measurements at each flow velocity with an estimated experimental error of ± (0.05% rdg+0.5 K). Further, the measured thermocouple temperature is corrected for radiation losses.
Case A: Zero-magnetic field
The variation in representative local temperature as a function of flow velocity is measured at the flame tip for the case of the zero-magnetic field. This is performed using an aluminum yoke instead of the magnetic yoke. Using a yoke to hold the magnets in place gives rise to two different impacts–a dynamic impact on the flow field and a magnetic impact. In this investigation, we consider only the magnetic impact on the flow field. To extract only the impact of the magnetic force on flames from the buoyancy force generated due to the presence of the yoke, a yoke made of aluminum possessing the exact geometry of the magnetic yoke is fabricated and all the baseline investigations are done in the presence of the aluminum yoke. The results are collected for flow velocities varying from 0.009 m/s to 0.051m/s. Figure 6 shows that local temperatures are underestimated by approximately 43.5 K due to radiation losses from the thermocouple tip (Table 1).
Case B: Increasing magnetic gradient field
The variation in highest local temperature with flow velocities in the presence of a gradient magnetic field whose strength was increasing from the burner tip is studied and is shown in Figure 7. It is observed that the local temperatures are underestimated by approximately 52K due to radiation losses from the thermocouple tip (Table 2).
Case C: Decreasing magnetic gradient field
The variation in local temperature in the presence of a gradient magnetic field whose strength was decreasing from the burner tip is studied and is shown in Figure 8. It is observed that the local temperatures are underestimated by approximately 52K due to radiation losses from the thermocouple tip (Table 3)
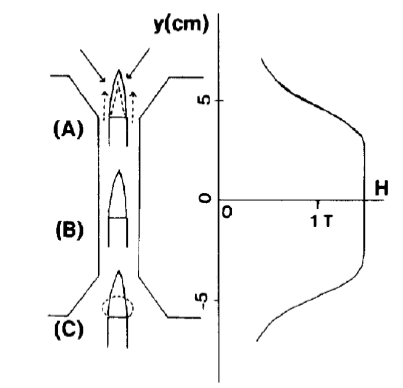
Figure 1 Direction of entrainment of air to flame under decreasing magnetic field (A).12
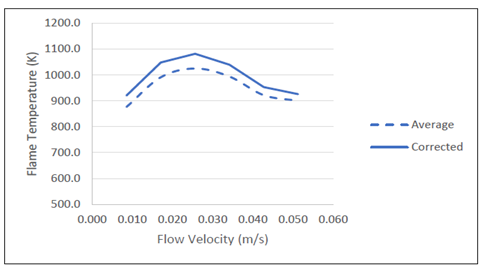
Figure 6 Variation of measured and corrected local temperature with flow velocity for zero-magnetic field.
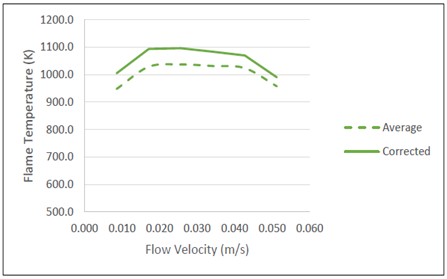
Figure 7 Variation of measured and corrected local temperature with flow velocity under increasing magnetic field gradient.
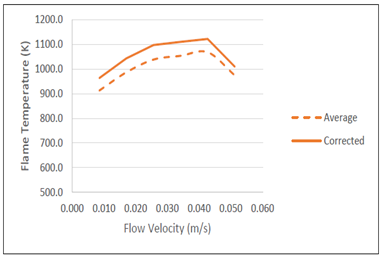
Figure 8 Variation of measured and corrected local temperature with flow velocity under decreasing magnetic field gradient.
Flow velocity (m/s) |
Average Tm (K) |
Corrected Tf (K) |
0.009 |
876.7 |
920.8 |
0.017 |
991.3 |
1048.5 |
0.026 |
1025.0 |
1082.1 |
0.034 |
994.2 |
1039.8 |
0.043 |
922.2 |
953.4 |
0.051 |
900.4 |
926.2 |
Table 1 Axial local temperature variation in the absence of gradient magnetic field
Flow velocity (m/s) |
Average Tm (K) |
Corrected Tf (K) |
0.009 |
948 |
1005.2 |
0.017 |
1028.7 |
1093.6 |
0.026 |
1037.2 |
1096.3 |
0.034 |
1031.6 |
1083.9 |
0.043 |
1023.8 |
1070.2 |
0.051 |
957.8 |
990.6 |
Table 2 Axial local temperature in case of increasing gradient magnetic field
Flow velocity (m/s) |
Average Tm (K) |
Corrected Tf(K) |
0.009 |
912.9 |
963.5 |
0.017 |
986.9 |
1043.4 |
0.026 |
1038.5 |
1097.6 |
0.034 |
1053.9 |
1110.6 |
0.043 |
1068.3 |
1122.3 |
0.051 |
974.6 |
1009.9 |
Table 3 Axial local temperature in case of decreasing gradient magnetic field
The values of the local temperatures under the influence of an increasing and decreasing gradient magnetic field and no applied magnetic field for the 0.81mm burner can be found in Table 4.
Figure 9 shows the impact of the gradient magnetic field on local temperature as a function of flow velocity. We can see that the trend of local temperature with the variation of fuel flow velocity can be roughly divided into three characteristic regions.
It is significant that the application of the decreasing magnetic gradient field is accompanied by an increase in local characteristic temperature. In case C, by subjecting the flame to a decreasing magnetic gradient field, oxygen from the surrounding gas is drawn towards the flame via the magnetic force exerted. Thus, better utilization of the oxidizer implies better combustion. This aid enhanced burning conditions by replenishing reactants and removing hot product gases from the flame zone and thus leading to higher temperatures. A reverse effect is expected in the case B when the increasing magnetic gradient field is applied as the magnetic forces are in the direction that quenches the combustion processes in a diffusion flame. Although the peak temperature in case B was found to be lower than that compared to case C, the local temperatures measured are still higher than the corresponding values for case A: zero-magnetic field. This behavior was not consistent with a previously published theory for the magnetic promotion of combustion.25 However, a similar anomaly was observed by Gillon30 where it was observed that the magnetic gradient field.
Flow velocity (m/s) |
NAMF (K) |
Increasing field (K) |
Decreasing field (K) |
0.009 |
920.8 |
1005.2 |
963.5 |
0.017 |
1048.5 |
1093.6 |
1043.4 |
0.026 |
1082.1 |
1096.3 |
1097.6 |
0.034 |
1039.8 |
1083.9 |
1110.6 |
0.043 |
953.4 |
1070.2 |
1122.3 |
0.051 |
926.2 |
990.6 |
1009.9 |
Table 4 Local temperature variation with and without magnetic gradient field
This study examined the behavior of propane jet diffusion flames exposed to a low-strength gradient magnetic field. Based upon the results of this investigation, the following conclusions have been drawn:
Future Work
There is scope for much future work that can be conducted further in this area of research to fully understand the complex nature of the interactions between magnetism and combustion:
None.
The author declares that there is no conflict of interest.

©2018 Boben, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.