This paper presents, the effect of elastic foundations on stochastic thermally induced post buckling response of functionally graded materials plates with uncertain material properties. Foundation stiffness parameters, material properties of each constituent's material, volume fraction index are taken as independent random input variables. The basic formulation is based on higher order shear deformation theory (HSDT) with von-Karman nonlinear kinematic using modified C0 continuity. A direct iterative based nonlinear finite element method (DISFEM) is successfully applied for FGMs plate to compute the mean and COV of the post buckling response of the FGM plates resting on elastic foundations. The results obtained by present outlined approach have been validated with the results available in literature and independent Monte Carlo simulation (MCS).

Keywords: fgm plates, elastic foundations, stochastic finite element method, uncertain material properties

The abrupt change in material properties across the interface between different materials can result in large inter-laminar stresses leading to delimitation, cracking, and other damage mechanisms which result from the abrupt change of the mechanical properties at the interface between the layers. Initially the uncertainty in material properties at micro level is finally reflected as macro level. Existing uncertain variations in material parameters may have significantly affects on fundamental structural characteristic and consequently these must affect the final design. Therefore, for accurate prediction of system behavior required for sensitive application favours a probabilistic/stochastic approach. The stochastic approach is a mathematical tool capable of handing uncertainties in the material properties to compute the statistic of structural response for example, post buckling response. FGMs are composite and microscopically heterogeneous in which the mechanical properties vary smoothly and continuously from one surface to the other.¹ This is achieved by gradually varying the volume fraction of the constituent materials. Typically, these materials are made from a mixture of ceramics and metal or a combination of different materials. The ceramic constituent of the material provides the high-temperature resistance due to its low thermal conductivity and protects the metal from oxidation. The structures subjected to thermal loading with spatial gradients in composition and microstructure is of considerable interest in numerous technological areas such as tribiology, optoelectronics, biomechanics, nanotechnology and high temperature technology. The graded transition in composition across an interface of two materials (metal and ceramics) can essentially reduce the thermal stresses and stress concentration at intersection with free surfaces. Due to the boundary constraints, compressive stresses acting on edges of the component arise due to thermal loading are induced, which may cause buckling, especially in thin walled structures. Buckling and post-buckling characteristics are one of the major design criteria for plates/panels for their optimal usage. Hence, it is important, to study the buckling and post-buckling characteristics of FGM plates under thermal loading for accurate, efficient and reliable design.

Large number of literature is available on deterministic analysis of FGM plate with mechanical thermal and thermo-mechanical buckling. In this direction, Feldman & Aboudi² studied the elastic buckling of functionally graded plate under in-plane compressive loadings with both simply supported and clamped edges. Praveen & Reddy³ investigated the response of functionally graded ceramic-metal plate, using finite element method. Reddy & Chin⁴ investigated the thermoelastical analysis of functionally graded cylinders and plates. Reddy⁵ presented the theoretical and finite element formulations for linear and nonlinear thermo-mechanical response of FGM plates employing higher order shear deformation theory. Vel & Batra⁶ presented an exact solution for the thermo-elastic deformation of functionally graded thick rectangular simply supported plates subjected to thermo-mechanical loadings. Javaheri & Eslami^7,8 obtained the buckling of the FGM plates for uniform in plane compressive loading and thermal loading using variational approach using classical plate theory (CLT). Najafizadeh & Eslami⁹ studied buckling analysis of circular plates of functionally graded materials under uniform radial compression. Liew et al.¹⁰ presented post-buckling behavior of the piezoelectric FGM plate using Galerkin-differential quadrature iteration method based on Reddy’s higher order shear deformation theory (HSDT).

Shen¹¹ presented the post-buckling analysis of functionally graded cylindrical panel under lateral pressure and temperature using Reddy’s higher order shear deformation theory and von-Karman-Donnell type nonlinearity. Liew et al.¹² presented the post-buckling behavior of the piezoelectric FGM plate using Fourier series using FSDT. Liew et al.¹³ studied the post buckling of piezoelectric FGM plates subjected to thermo-electro-mechanical loading. Shen¹⁴ presented the post-buckling response of axially loaded FG cylindrical panels subjected to thermal loading using semi-analytical approach based on Reddy’s HSDT. Yang & Shen¹⁵ evaluated nonlinear bending and post-buckling response of the FG rectangular plate using a semi-analytical approach with Reddy’s HSDT. Woo et al.¹⁶ examined the post-buckling of functionally graded material plates and shallow cylindrical shells under thermo-mechanical loading using an analytical solution with mixed Fourier series. Ma & Wang^17,18 presented bending and buckling of FGM circular plate based on CLPT and third order plate theory. Lanhe¹⁹ presented a semi-analytical solution for the thermal buckling of FGM rectangular simply supported plate subjected to uniform temperature rise and gradient through the thickness of plate, using the first-order shear deformation theory. Die²⁰ investigated the thermo mechanical analysis of functionally graded material (FGM) plates using element-free Galerkin method. Bhangale et al.²¹ studied the linear thermo-elastic buckling and free vibration behavior of functionally graded truncated conical shells Wu et al.²² evaluated the post buckling response of functionally graded materials plates based on the CLT with von-Karman nonlinear kinematics with analytically approach and Chebyshev polynomials.

All the above literatures are based on the assumptions of the complete determinacy of structural parameters. In the deterministic analysis of structures, the variations in the material parameters are neglected and mean value of system parameters are used in the analysis, which gives only mean response and unaccounted the deviation caused by inherent random material properties.^23,24 Roshan studied the buckling and vibration of functionally graded non-uniform circular plates resting on Winkler foundation. A part from other side, the mechanical properties depends on a wide variety of variable at micro level, for example the material properties of constituent materials, variation in FGM thickness, volume fraction index etc., These variables are statistical in nature; therefore, the mechanical properties of a FGM structures should be quantified probabilistically. The influence of these micro level variables on the macro level effective properties of FGM has been studied numerically using proposed methods. These variations ultimately lead to the variation in the response of the structure. Relatively little efforts have been made in the past by the researchers and investigators on the prediction of response statistics of the structures made of laminated composites and FGMs plates having random system properties. In this direction, Singh et al.^25‒34 invested the post buckling response and natural frequencies of laminated composite plate with random system properties with or without elastic foundation.

Further, Yang et al.^27,28 evaluated the second-order statistics for elastic buckling of FGM plates with randomness in the material properties using stochastic finite element method via first-order shear deformation theory. Onkar et al.^29‒31 investigated the generalized buckling of laminated composite plate with random material properties using classical plate theory (CLT) combined with FOPT. Kirtipornchai et al.³⁰ studied the random vibration of functionally graded laminates in thermal environments composed by the third order shear deformation theory with random thermo mechanical properties using the first order perturbation technique incorporating mixed type and semi-analytical approach to derive the standard eigen value problem. Lal et al.^32‒39 investigated the effect of random system properties on buckling of laminated composite plates supported with/without elastic foundation with and without subjected to thermal environment using HSDT based C0 linear and nonlinear FEM combined with and without direct iterative method in conjunction with FOPT. Lal A et al.⁴⁰ investigated the post buckling response of functionally graded plate subjected to mechanical and thermal loadings with random material properties Jagtap et al.⁴¹ investigated the thermo mechanical elastic post buckling of functionally graded material plate with random material properties Lal A & Singh⁴² analysed the Stochastic mechanical and thermal post buckling response of functionally graded material plates with circular and square holes having material randomness.

It is evident from the available literatures that the studies of stochastic buckling response of geometrically nonlinear FGM plates resting on elastic foundations, subjected to thermal loading involving randomness in material properties of constituent materials and foundation stiffness parameters using computationally efficient direct iterative based C0 nonlinear FEM in combined with mean cantered FOPT not dealt by the researchers. In the present study, the paper is organised as follows. Section 1 gives the brief introduction of related problem with justification and literature surveys based on deterministic and probabilistic analysis. The brief description of the geometric configuration, material properties, foundation stiffness parameters, coefficients of thermal expansion and theoretical formulations of the problem using finite element methods are given in section 2 and 3. In section 4 governing equation of the problem is presented. The solution methodology of probabilistic finite element is presented in section5.Section 6 explains the results and discussion followed by validation studies and section 7 accomplished the conclusions. The numerical results are presented in terms of tables which can suit the benchmark of future work.^43‒46

Consider a square FGM plate consist of metal and ceramic at the top and bottom layer of length a, width b, and total thickness h, defined in (x, y, z) system with x- and -y axes located in the middle plane and its origin placed at the corner of the plate. Let $\left(\overline{u},\overline{v},\overline{w}\right)$ be the displacement parallel to the (x, y, z) axes respectively as shown in Figure 1. The properties of the FGM plate are assumed to be vary through the thickness of the plate only, such that the top surface z=h/2 is ceramic-rich and the bottom surface z=-h/2 is metal reach. The effective thermal properties of the FGMs plate.⁴⁷

$\begin{array}{l}E\left(z,T\right)=E_b\left(T\right)+\left[E_t\left(T\right)-E_b\left(T\right)\right]V_c\left(z\right)\\ \alpha \left(z,T\right)={\alpha }_b\left(T\right)+\left[{\alpha }_t\left(T\right)-{\alpha }_b\left(T\right)\right]V_c\left(z\right)\\ \rho \left(z,T\right)={\rho }_b+\left[{\rho }_t-{\rho }_b\right]V_c\left(z\right)\\ k\left(z,T\right)=k_b+\left[k_t-k_b\right]V_c\left(z\right)\end{array}$    (1)

Where, t and b represent to the ceramic and metal constituents, respectively. With E, α, ρ and k are the effective young modulus, thermal expansion coefficient, density and thermal conductivity respectively. The ceramic volume fraction index V_C is the function of coordinate in the thickness direction, z and is given by

$V_C\left(z\right)={\left(0.5+\frac{z}{h}\right)}^n,-h/2\le z\le h/2,0\le n\prec \infty$     (2)

Where, n is the power index law and is always positive. For n =0, the plate is fully ceramic. With n = 1, the composition of ceramic and metal is linear. The Poisson’s ratio v depends weakly on temperature change and is assumed to constant.

Displacement field model

In the present study the higher order shear deformation theory with C^° continuity (modified of C¹ continuity proposed by Reddy’s [1] with extra degree of freedom) has been employed,^25‒33

$\overline{u}=u+z{\psi }_x-z^{3}4/3h^2({\psi }_x+\partial w/\partial x)=u+f_1(z){\psi }_x+f_2(z)\partial w/\partial x,$

$\overline{v}=v+z{\psi }_y-z^{3}4/3h^2({\psi }_y+\partial w/\partial y)=v+f_1(z){\psi }_y+f_2(z)\partial w/\partial y,$ and $\overline{w}=w$    (3)

Where $\overline{u}$ ,$\overline{v}$ and $\overline{w}$ denote the displacements of a point along the (x, y, z) coordinates, u, v, and w are corresponding displacements of a point on the mid plane.${\psi }_x$ and ${\psi }_y$ are the rotations of normal to the mid plane about the y-axis and x-axis respectively, with ${\theta }_x=\partial w/\partial x$ and

${\theta }_y=\partial w/\partial y$ $f_1\left(z\right)=C_{1}z-C_2{z}^3$ $f_2\left(z\right)=-C_4{z}^3$ with $C_1=1,\text{}{C}_2=C_4=4h^2/3$ .

The displacement vector for the modified models is

$\left\{\Lambda \right\}={\left[\begin{array}{ccccccc}u& v& w& {\theta }_y& {\theta }_x& {\psi }_y& {\psi }_x\end{array}\right]}^T$  (4)

Strain displacement relations

For the structures considered here, the relevant strain vector consisting of strains in terms of mid-plane deformation, rotation of normal and higher order terms associated with the displacement for isotropic layer are as.³⁵

$\left\{\epsilon \right\}=\left\{{\epsilon }_l\right\}+\left\{{\epsilon }_{nl}\right\}-\left\{{\overline{\epsilon }}_t\right\}$    (5)

where$\left\{{\epsilon }_l\right\}$ ,$\left\{{\epsilon }_{nl}\right\}$ and $\left\{{\overline{\epsilon }}_t\right\}$ are the linear and nonlinear strain (von-Karman sense) vectors, thermal strain vector, respectively. The thermal strain vector $$\left\{{\overline{\epsilon }}_t\right\}$$ given in Equation (5) is expressed as.²³

$\left\{{\overline{\epsilon }}_t\right\}=\left\{\begin{array}{c}\left\{{\overline{\epsilon }}_x\right\}\\ \left\{{\overline{\epsilon }}_y\right\}\\ \left\{{\overline{\epsilon }}_{xy}\right\}\\ \begin{array}{l}\left\{{\overline{\epsilon }}_{yz}\right\}\\ \left\{{\overline{\epsilon }}_{zx}\right\}\end{array}\end{array}\right\}=\Delta T\left\{\begin{array}{l}\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ {\alpha }_{12}\\ 0\end{array}\\ 0\end{array}\right\}$  (6)

The linear $\left\{{\epsilon }_l\right\}$ strain vector can be obtained by³² and the nonlinear strain can be written as.³⁵

${\epsilon }_{nl}=\frac{1}{2}\left[A_{nl}\right]\left\{\varphi \right\}$   (7)

where

$A_{nl}=\frac{1}{2}\left[\begin{array}{cc}{w}_{,x}& 0\\ 0& w_{,y}\\ w_{,x}& w_{,y}\\ 0& 0\\ 0& 0\end{array}\right]$ and$\varphi =\left\{\begin{array}{c}{w}_{,x}\\ w_{,y}\end{array}\right\},$ (8)

where α₁, α₂ and α₁₂ are coefficients of thermal expansion in the x, y, z direction respectively which can be obtained from the thermal coefficients in the longitudinal (α_l) and transverse (α₂) directions of the ceramic and metal using transformation matrix and $\Delta T$ is the uniform temperature change.

The temperature field for uniform temperature change is expressed as

$T(z)=T_0+(T_t-T_b)$     (9)

where T (z) is expressed as⁴⁷

$T(z)=T_b+(T_t-T_b)\eta (z)$   (10)

For uniform temperature rise, the initial (T₀) and bottom (T_b) uniform and non-uniform temperature of the plate is assumed to be 300^°K, 600^°K respectively.^22,27

• Stress strain relation
• The constitutive relationship between stress and strain vectors in plane stress state for an isotropic layer accounting thermal effect can be written as⁴⁷

$\left\{\sigma \right\}=\left[\overline{Q}\right]\left\{\epsilon \right\}$ or$\left\{\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\sigma }_{xy}\\ {\sigma }_{yz}\\ {\sigma }_{xz}\end{array}\right\}=\left[\begin{array}{ccccc}{\overline{Q}}_{11}& {\overline{Q}}_{12}& {\overline{Q}}_{16}& 0& 0\\ {\overline{Q}}_{12}& {\overline{Q}}_{22}& {\overline{Q}}_{26}& 0& 0\\ {\overline{Q}}_{16}& {\overline{Q}}_{26}& {\overline{Q}}_{66}& 0& 0\\ 0& 0& 0& {\overline{Q}}_{44}& 0\\ 0& 0& 0& 0& {\overline{Q}}_{55}\end{array}\right]\left\{\left\{\begin{array}{c}{\epsilon }_x\\ {\epsilon }_y\\ {\epsilon }_{xy}\\ {\epsilon }_{yz}\\ {\epsilon }_{zx}\end{array}\right\}-\left\{\begin{array}{c}{\lambda }_1\\ {\lambda }_2\\ {\lambda }_{12}\\ 0\\ 0\end{array}\right\}\Delta T\right\}$ (11)

Where $${\lambda }_1={\overline{Q}}_{11}{\alpha }_1+{\overline{Q}}_{12}{\alpha }_2+{\overline{Q}}_{16}{\alpha }_{12};{\lambda }_2={\overline{Q}}_{12}{\alpha }_1+{\overline{Q}}_{22}{\alpha }_2+{\overline{Q}}_{26}{\alpha }_{12};{\lambda }_{12}={\overline{Q}}_{16}{\alpha }_1+{\overline{Q}}_{26}{\alpha }_2+{\overline{Q}}_{66}{\alpha }_{12}$$

where $\left\{{\overline{Q}}_{ij}\right\}$ ,$\left\{\sigma \right\}$ and $$\left\{\epsilon \right\}$$ are transformed stiffness matrix, stress and strain vectors of the isotropic lamina, respectively,${\alpha }_1$ ,${\alpha }_2$ ,${\alpha }_{12}$ are the thermal expansion coefficients along x,y,z directions, which are obtained from the thermal coefficients in the longitudinal(${\alpha }_1,$ ) and transverse (${\alpha }_t$ ) directions of the FGMs using transformation matrix. ∆T is the temperature rise. The constitutive relationship between stress resultants per unit length and mid-plain strains and curvatures is written in matrix form

$\left\{\begin{array}{l}{N}_i\\ M_i\\ P_i\end{array}\right\}=\left[\begin{array}{cccc}\begin{array}{c}{A}_{ij}\\ B_{ij}\\ E_{ij}\\ \end{array}& \begin{array}{c}{B}_{ij}\\ D_{ij}\\ F_{ij}\\ \end{array}& \begin{array}{c}{E}_{ij}\\ F_{ij}\\ H_{ij}\\ \end{array}& \end{array}\right]\left\{\begin{array}{l}{\epsilon }_j^0\\ K_j^0\\ K_j^2\end{array}\right\}-\left\{\begin{array}{l}{N}_i^T\\ M_i^T\\ P_i^T\end{array}\right\}(i,j=1,2,6)$   (12)

$\left\{\begin{array}{l}{Q}_2\\ Q_1\end{array}\right\}=\left[\begin{array}{l}{A}_{4j}{D}_{4j}\\ A_{5j}{D}_{5j}\end{array}\right]\left\{\begin{array}{l}{\epsilon }_j^0\\ K_j^2\end{array}\right\};\left\{\begin{array}{l}{R}_2\\ R_1\end{array}\right\}=\left[\begin{array}{l}{D}_{4j}{F}_{4j}\\ D_{5j}{F}_{5j}\end{array}\right]\left\{\begin{array}{l}{\epsilon }_j^0\\ K_j^2\end{array}\right\}(j=4,5)$    (13)

with

$N_i={[N_{ix}{N}_{iy}{N}_{ixy}]}^T,M_i={[M_{ix}{M}_{iy}{M}_{ixy}]}^T,P_i={[P_{ix}{P}_{iy}{P}_{ixy}]}^T$

where A_ij, B_ij etc., are the plate stiffness defined in Appendix. Thermal stress resultants

$N\frac{T}{i}={[N_{tx}{N}_{ty}{N}_{txy}]}^T,M_i^T={[M_{tx}{M}_{ty}{M}_{txy}]}^T,P_i^T={[P_{tx}{P}_{ty}{P}_{txy}]}^T$ are calculated by

$$\left[\begin{array}{ccc}{N}_i^T& M_i^T& P_i^T\end{array}\right]={\displaystyle \sum _{m=1}^N{\displaystyle {\int }_{-h/2}^{h/2}\left\{\begin{array}{l}\overline{Q_{11}}{\alpha }_1+\overline{Q_{12}}{\alpha }_2+\overline{Q_{16}}{\alpha }_{12}\\ \overline{Q_{12}}{\alpha }_1+\overline{Q_{22}}{\alpha }_2+\overline{Q_{26}}{\alpha }_{12}\\ \overline{Q_{16}}{\alpha }_1+\overline{Q_{26}}{\alpha }_2+\overline{Q_{66}}{\alpha }_{12}\end{array}\right\}}}\left(1,z,z^3\right)\Delta Tdz$$

For FGM material the elastic constant are defined as.⁴⁷

$${\overline{Q}}_{11}={\overline{Q}}_{22}=\frac{E(z,T)}{1-{\nu }^2},{\overline{Q}}_{12}=\frac{\nu E(z,T)}{1-{\nu }^2},{\overline{Q}}_{44}={\overline{Q}}_{55}={\overline{Q}}_{66}=\frac{E(z,T)}{2(1+\nu )}$$     (14)

The value of E is taken from Eq. (1).

• Strain energy of the plate

The strain energy of the plate is given by

${\Pi }_1=\frac{1}{2}{{\displaystyle \underset{V}{\int }\left\{\epsilon \right\}}}^T\left[\sigma \right]dv$    (15)

$U=\frac{1}{2}{\displaystyle \underset{}{\int }{\displaystyle {\int }_R^{}\left[N_{ix}{\epsilon }_{xx}+N_{iy}{\epsilon }_{yy}+N_{ixy}{\gamma }_{xy}+Q_1{\gamma }_{xz}+Q_2{\gamma }_{yz}\right]}}dxdy$      (16)

Potential energy due to thermal stresses

The potential energy (${\Pi }_2$ ) storage by thermal load (uniform and transverse change in temperature across the thickness) Due to change in temperature, pre buckling stresses, i.e. in plane thermal compressive stress resultants in the plate are generated. These resultants are the reason for the buckling. The potential energy due to the in plane thermal stress resultants is expressed as

$\begin{array}{l}{\prod }_2=\frac{1}{2}{\displaystyle {\int }_A\left[N_{xtm}{\left(w{,}_x\right)}^2+N_{ytm}{\left(w{,}_y\right)}^2+2N_{xytm}\left(w{,}_x\right)\left(w{,}_y\right)\right]}dA\\ =\frac{1}{2}{{\displaystyle {\int }_A\left\{\begin{array}{c}w{,}_x\\ w{,}_y\end{array}\right\}}}^T\left[\begin{array}{cc}{N}_{xtm}& N_{xytm}\\ N_{xytm}& N_{ytm}\end{array}\right]\left\{\begin{array}{c}w{,}_x\\ w{,}_y\end{array}\right\}dA\end{array}$    (17)

Where, N_xtm, N_ytm and N_xytm are Thermo mechanical in-plane compressive stress resultant per unit length. with N_xtm = N_xm - N_xt ,N_xytm = N_xym - N_xyt and N_ytm = N_ym - N_yt .

Using finite element method⁵ and summing over the entire element the Eq. (17) can be written as

$W={\displaystyle \sum _{e=1}^{NE}{W}^{\left(e\right)}}={\displaystyle \sum _{e=1}^{NE}{\left\{{\Lambda }^{\left(e\right)}\right\}}^T{\lambda }_T\left[K_g{}^{{}^{\left(e\right)}}\right]{\left\{\Lambda \right\}}^{\left(e\right)}}={\lambda }_T{\left\{q\right\}}^T\left[K_g\right]\left\{q\right\}$

Where ${\lambda }_T$ ,$\left[K_g\right]$ are defined as critical thermal buckling temperature and global geometric stiffness matrix defined in appendix respectively.

Using Eqs. (5), (6) and (7), Eq. (16) can be written in expanded form as

$\begin{array}{l}U=\frac{1}{2}{\displaystyle {\int }_A{\left\{{\overline{\epsilon }}_l\right\}}^T\left[D\right]}\left\{{\overline{\epsilon }}_l\right\}dA+\frac{1}{2}{\displaystyle {\int }_A{\left[{\overline{\epsilon }}_l\right]}^T}\left[D_3\right]\left\{A\right\}\left\{\theta \right\}dA\\ +\frac{1}{2}{{\displaystyle {\int }_A{\left\{A\right\}}^T\left\{\theta \right\}}}^T\left[D_4\right]\left\{{\overline{\epsilon }}_l\right\}dA+\frac{1}{2}{\displaystyle {\int }_A{\left\{A\right\}}^T{\left\{\theta \right\}}^T}\left[D_5\right]\left\{A\right\}\left\{\theta \right\}dA\end{array}$    (18)

where [D], [D₃], [D₄] and [D₅] are the laminate stiffness matrices defined in appendix and $\left\{{\overline{\epsilon }}_l\right\}$ is the linear mid-plane strain vector.²⁵

The strain energy function is computed for each element and then summed over all the elements to get the total strain energy.³³ Following this procedure, Eq. (18), can be written as

$U={\displaystyle \sum _{e=1}^{NE}{U}^{\left(e\right)}}={\displaystyle \sum _{e=1}^{NE}{\left\{\Lambda \right\}}^{{{}^{\left(e\right)}}^T}{\left[K_l+K_{nl}\left(\Delta \right)\right]}^{\left(e\right)}{\left\{\Lambda \right\}}^{\left(e\right)}}={\left\{q\right\}}^T\left[K_i+K_{nl}\left(q\right)\right]\left\{q\right\}$   (19)

Where $\left[K_l\right]$ ,$\left[K_{nl}\right]$ and $\left\{q\right\}$ are defined as global linear, nonlinear stiffness matrix and displacement vector respectively and defined in appendix.

External work done

Due to uniform temperature change, pre-buckling stresses in the FGM plate are generated. The in-plane pre-buckling stress resultants per unit length are reason for buckling. The work done (W) by the in-plane stress resultants in producing out of plane displacement ‘w’ is expressed as

$\begin{array}{l}W=\frac{1}{2}{\displaystyle {\int }_A\left[N_x{\left(w{,}_x\right)}^2+N_y{\left(w{,}_y\right)}^2+2N_{xy}\left(w{,}_x\right)\left(w{,}_y\right)\right]}dA\\ =\frac{1}{2}{{\displaystyle {\int }_A\left\{\begin{array}{c}w{,}_x\\ w{,}_y\end{array}\right\}}}^T\left[\begin{array}{cc}{N}_x& N_{xy}\\ N_{xy}& N_y\end{array}\right]\left\{\begin{array}{c}w{,}_x\\ w{,}_y\end{array}\right\}dA\end{array}$  (20)

Where, N_x, N_y and N_xy are thermal in-plane thermal compressive stress resultant per unit length.

Using finite element method⁵ and summing over the entire element the Eq. (20) can be written as

$W={\displaystyle \sum _{e=1}^{NE}{W}^{\left(e\right)}}={\displaystyle \sum _{e=1}^{NE}{\left\{{\Lambda }^{\left(e\right)}\right\}}^T{\lambda }_T\left[K_g{}^{{}^{\left(e\right)}}\right]{\left\{\Lambda \right\}}^{\left(e\right)}}={\lambda }_T{\left\{q\right\}}^T\left[K_g\right]\left\{q\right\}$     (21)

 Where${\lambda }_T$ ,$\left[K_g\right]$ are defined as critical thermal buckling temperature and global geometric stiffness matrix defined in appendix respectively.

• Strain energy due to elastic foundations
• Strain energy due to elastic foundations can be expressed as:

$\begin{array}{l}\pi =\frac{1}{2}{\displaystyle {\int }_A\left\{K_1{w}^2+K_2\left[{\left(w_{,x}\right)}^2+{\left(w_{,y}\right)}^2\right]\right\}dA},\\ \pi =\frac{1}{2}{\displaystyle {\int }_A{\left\{\begin{array}{c}w\\ w_{,x}\\ w_{,y}\end{array}\right\}}^T\left[\begin{array}{ccc}{K}_1& 0& 0\\ 0& K_2& 0\\ 0& 0& K_2\end{array}\right]\left\{\begin{array}{c}w\\ w_{,x}\\ w_{,y}\end{array}\right\}dA}\end{array}$    (22)

In the present study a C^° nine-noded isoparametric finite element with 7 DOFs per node is employed i.e., (u,v,w,.${\psi }_x$ ,${\psi }_{y,}{\theta }_x,{\theta }_y)$ is employed. For this type of element, the displacement vector and the element geometry are expressed as

$\left\{\Lambda \right\}={\displaystyle \sum _{i=1}^{NN}{\phi }_i}{\left\{\Lambda \right\}}_i;x={\displaystyle \sum _{i=1}^{NN}{\phi }_i}{x}_i;$ and$y={\displaystyle \sum _{i=1}^{NN}{\phi }_i}{y}_i$       (23)

where ${\phi }_i$ is the interpolation function for the i^th node,${\left\{\Lambda \right\}}_i$ is the vector of unknown displacements for the i^th node, NN is the number of nodes per element and x_i and y_i are Cartesian Coordinate of the i^th node. The linear mid plane strain vector can be expressed in terms of mid plane displacement field and then the energy is computed for each element and then summed over all the elements to get the total strain energy.³³ Following this, and using Eq. (23), Eq. (15) can be written as

${\Pi }_1={\displaystyle \sum _{e=1}^{NE}{\Pi }_1{}^{\left(e\right)}}$    (24)

where, NE is the number of elements and U^(e) is the elemental total potential energy which can be expressed

${\Pi }_1={\displaystyle \sum _{e=1}^{NE}\left[\frac{1}{2}{\left\{{\Lambda }^{\left(e\right)}\right\}}^T\left[K_l{{}^{*}}^{{}^{\left(e\right)}}+K_{nl}{}^{{}^{\left(e\right)}}{\left\{\Lambda \right\}}^{\left(e\right)}\right]{\left\{\Lambda \right\}}^{\left(e\right)}-{\left\{{\Lambda }^{\left(e\right)}\right\}}^T\left[F_t^{{}^{\left(e\right)}}\right]\right]}$= $=\frac{1}{2}{\left\{q\right\}}^T\left[K_l+K_{nl}\left\{q\right\}\right]\left\{q\right\}-{\left\{q\right\}}^T\left[F^T\right]$   (25)

With

$\left[K_l\right]=\left[K_b\right]+\left[K_s\right]$

where global bending stiffness matrix [K_b], shear stiffness matrix[K_s], global nonlinear stiffness matrix [K_nl], global displacement vector {q}and thermal load vector [F] are defined as appendix.

• Thermal post buckling anal thermal post buckling analysis

Using finite element model (Eq. (23), Eq. (15) can also be written as

${\Pi }_2$ $=\frac{1}{2}{\displaystyle \sum _{e=1}^{NE}{\left\{\Lambda \right\}}^{T\left(e\right)}\lambda {\left[K_g\right]}^{\left(e\right)}{\left\{\Lambda \right\}}^{\left(e\right)}dA}$ $=\frac{1}{2}\lambda {\left\{q\right\}}^T\left[K_g\right]\left\{q\right\}$    (26)

Were, $\lambda$ and $\left[K_g\right]$ are defined as the thermal post buckling load parameters and the global geometric stiffness matrix, respectively.

${\Pi }_2$  

• Strain energy due to elastic foundation

Using finite element notation after summed over all the element can be written as:

${\Pi }_3=({\displaystyle \sum _{e=1}^{NE}{\Pi }_{{}^{fl}}^{\left(e\right)}+{\displaystyle \sum _{e=1}^{NE}{\Pi }_{{}^{fnl}}^{\left(e\right)})}},{\Pi }_{{}^{fl}}^{\left(e\right)}=\frac{1}{2}{\displaystyle \underset{A}{\int }{\left\{{\Lambda }^{(e)}\right\}}^T{\left[K_{fl}\right]}^{\left(e\right)}\left\{{\Lambda }^{(e)}\right\}dA},{\Pi }_{{}^{fnl}}^{\left(e\right)}=\frac{1}{2}{\displaystyle \underset{A}{\int }{\left\{{\Lambda }^{(e)}\right\}}^T{\left[K_{fnl}\right]}^{\left(e\right)}\left\{{\Lambda }^{(e)}\right\}dA}$  (27)

here ${\left[K_{fl}\right]}^{\left(e\right)}$ ,and ${\left[K_{fnl}\right]}^{\left(e\right)}$ are the elemental linear and nonlinear foundation stiffness matrices respectively.

Adopting Gauss quadrature integration numerical rule, the element stiffness and geometric stiffness respectively can be obtained by transforming expression in x, y coordinate system to natural coordinate system ᶓ, η.

The governing equation for thermally induced post buckling load of the plate analysis can be derived using the Lagrange’s equation of motion.

$\delta {\displaystyle {\int }_{t_1}^{t_2}\left(U-W-\pi \right)}*TdT=0$   (28)

Substituting Equations (25), (26) and (27) into Equation (28), ones obtain as in the form of non linear generalized eigen-value problem as

$[K]\left\{q\right\}+\left[M\right]\left\{\ddot{q}\right\}=0$    (29)

where,

The above Eq. (24) is the post buckling equation which can be solved literately as a linear eigen value problem assuming that the plate is vibrating in its principal mode in each iteration. For each iteration, the Eq. 19 can be expressed as generalized eigen-value problem as:

$\left[[K]-\lambda \left[M\right]\right]\left\{q\right\}=0$     (30)

where $\lambda =\omega$ with ω is the natural frequency of the plate.

Equation (29) is the post buckling problem which is random in nature, being dependent on the system properties. Consequently, the natural frequency and mode shapes are random in nature. In deterministic environment, the Eq. (30) is evaluated using eigen-value formulation and solved employing a direct iterative methods, Newton-Rapsion methods, incremental methods etc. However, in random environment, it is not possible to solve the problem using the above mentioned methods without changing the nature of the equation. Based on this, the direct iterative method combined with nonlinear finite element method, i.e., (DISFEM) with a reasonable accuracy is used to determine the second-order statistics (mean and standard deviation) of post buckling response of the FGM plates. The nonlinear eigen-value problem as given in Eq. 30 is solved by employing a direct iterative method in conjunction with perturbation technique assuming that the random changes in eigenvector during iterations does not affect much the nonlinear stiffness matrix with the steps^24‒46

We consider a class of problems where the zero mean random variation is very small when compared to the mean part of random system properties. In general, without any loss of generality any arbitrary random variable can be represented as the sum of its mean and a zero mean random variable, expressed by superscripts ‘d’ and ‘r’, respectively,^25,26

$K=K^d+K^r,K_g=K_g^d+K_g^r,{\lambda }_i={\lambda }_i{}^d+{\lambda }_i{}^r,q_i=q_i{}^d+q_i{}^r,$  (32)

The parameter p indicates the size of eigen problem.

Consider a class of problems where the random variation is very small as compared to the mean part of material properties. Further it is quite logical to assume that the dispersions in the derived quantities like andare also small as compared to their mean values. By substituting Eq. (32) in Eq. (30) and collecting same order of the magnitude term and keeping only up to first order terms, one obtains as,²⁴

Zeroth order:$$\left[K_{}^d\right]\left\{q_i^d\right\}={\lambda }_i^d\left[K_g^{}\right]\left\{q_i^d\right\}$$        (33)

First order:$\left(K^d\right)\left\{q_i{}^r\right\}+\left(K^r\right)q_i{}^d={\lambda }_i{}^d\left[K_g^r\right]\left(q_i{}^d\right)+{\lambda }_i{}^d\left[K_g^d\right]\left\{q_i{}^r\right\}+{\lambda }_i{}^r\left[K_g^d\right]\left(q_i{}^d\right),$        (34)

Eq. (33) is the deterministic equations relating to the mean eigen-values and corresponding mean eigenvectors, which can be determined by conventional eigen solution algorithms. For solving first order Eq. (34) the first order perturbation approach is employed.

According to the orthogonality properties, the normalized eigenvector meet the followi ng conditions.

${\left\{q_i{}^d\right\}}^T\left[K_g{}^d\right]\left\{q_i{}^d\right\}={\delta }_{ij}$    (35)

${\left\{q_i{}^d\right\}}^T\left[K^d\right]\left\{q_i{}^d\right\}={\delta }_{ij}{\lambda }_i{}^d$ . $\left(i,j\right)=1,2,...,p$     (36)

where ${\delta }_{ij}$ is the Kronecker delta.

The eigenvectors, which meet orthogonality, conditions after being properly, normalized form a complete orthonormal set and any vector in the space can be expressed as their linear combination of these eigenvectors. Hence, the i^th random part of the eigenvectors can be expressed as

$C_{ii}{}^r=0$ .$i\ne j$ ,$C_{ii}{}^r=0$ , i=1, 2, …. , p (37)

where$C_{ij}{}^r$ s are small random coefficients to be determined.

Substituting Eq. (37) in Eq. (34), premultiplying, the first by ${\left\{q_i{}^d\right\}}^T$ and second by ${\left\{q_j{}^d\right\}}^T$ , $\left(j\ne i\right)$ respectively and making use of orthogonality Eq. (36), one obtains as

${\lambda }_i{}^r={\left\{q_i{}^d\right\}}^T\left[K^r\right]\left\{q_i{}^d\right\}-{\lambda }_i{}^d{\left\{q_i{}^d\right\}}^T\left[K_g{}^r\right]\left\{q_i{}^d\right\}$  (38)

$C_{ij}{}^r=\frac{\left\{q_j{}^d\right\}\left[K^r\right]\left\{q_i{}^d\right\}-{\lambda }_i{}^d\left\{q_j{}^d\right\}\left[K_g{}^r\right]\left\{q_i{}^d\right\}}{\left({\lambda }_i{}^d-{\lambda }_j{}^d\right)}$  (39)

Substituting Eq. (34) into Eq. (32), we obtain

$\left\{q_i{}^r\right\}={\displaystyle \sum _{j=1}^p\left\{q_i{}^d\right\}}\frac{{\left\{q_j{}^d\right\}}^T\left[K^r\right]\left\{q_i{}^d\right\}-{\lambda }_i{}^d{\left\{q_j{}^d\right\}}^T\left[K_g{}^r\right]\left\{q_i{}^d\right\}}{{\lambda }_i{}^d-{\lambda }_j{}^d}$ . $i\ne j$    (40)

For the present case $\lambda$ ,$\left\{q\right\}$ ,$\left[K\right]$ ,$\left[K_f\right]$ , $\left[K_f\right]$ and h are random because of random geometric and material properties. Let $b_1^R$ ,$b_2^R$ ,$b_3^R$ ,$b_q^R$ …, denote random variables (system properties). The random variables (RVs) can be expressed as

$$b_j{}^R=b_j{}^d+b_j{}^r$$   (41)

The FEM in conjunction with FOPT has been found to be accurate and efficient. According to this method, the random variables are expressed by Taylor’s series expansion. The expression only up to the first-order terms and neglecting the second- and higher-order terms are

$\begin{array}{l}{\lambda }_i{}^r={\displaystyle \sum _{j=1}^p{\lambda }_i{{}_{,}^d}_j}{h}_j{}^r;\left\{q_i{}^r\right\}={\displaystyle \sum _{j=1}^p\left\{q_i{{}^d}_{,}{}_j\right\}}{h}_j{}^r;\\ \left[K^r\right]={\displaystyle \sum _{j=1}^p\left[K^d{{}_{,}}_j\right]}{h}_j{}^r;\left[K_g{}^r\right]={\displaystyle \sum _{j=1}^p\left[K_g{{}^d}_{,}{}_j\right]}{h}_j{}^r\end{array}$     (42)

Where (, j) denotes the partial differentiation with respect to $b_j$ .

On substitution of Eq. (42) into Eq. (38), one obtain as

${\lambda }_i{{}_{,}^d}_j={\left\{q_i{}^d\right\}}^T\left[K^d{{}_{,}}_j\right]\left\{q_i{}^d\right\}-{\lambda }_i{}^d{\left\{q_i{}^d\right\}}^T\left[K_g{{}^d}_{,}{}_j\right]\left\{q_i{}^d\right\}$    (43)

The variance of the eigen-values can now be expressed as

$Var\left({\lambda }_i\right)={\displaystyle \sum _{j=1}^q{\displaystyle \sum _{k=1}^q{\lambda }_{i,j}^d}}{\lambda }_{i,k}^{d}Cov\left(b_j{}^r,b_k{}^r\right)$    (44)

where $Cov\left(b_j{}^r,b_k{}^r\right)$ is the covariance between $b_j{}^r$ and $b_k{}^r$ . The standard deviation (SD) is obtained by the square root of the variance.

A DISFEM probabilistic approach outlined in previous subsection for post buckling response of the elastically supported FGM plate in thermal environments with random material properties has been presented through numerical examples. The present probabilistic approach has been validated by comparing the results with those available in literature and independent MCS. Typical results for mean and coefficient of variance {COV (=SD/mean)} of the post buckling response for FGM square plate in the given following text are presented using MATLAB 7.10.0 (R2010a) software. A nine nodded Lagrangian isoparametric element with 63 degree of freedom per node for the present HSDT model has been used throughout the study. Based on the convergence study, a (4 x 4) mesh size has been used for numerical computation. Due to the linear nature of variation as mentioned earlier and passing through the origin, the results are only presented by COV of the system properties equal to 0.1. However, the obtained results revealed that the stochastic approach would be valid up to COV=0.2.^44,45 Moreover, the presented results would be sufficient to extrapolate the results for other COV values keeping in mind the limitation of the FOPT. The assumed basic random input variables (b_i) are sequenced and written as

$b_1=E_c,b_2=E_m,b_3={\upsilon }_c,b_4={\upsilon }_m,b_5=n,b_6=k_1,b_7=k_2$

where $E_c,E_m,{\upsilon }_c,{\upsilon }_m,n,k_1\text{, }{k}_2$ are Young’s moduli, Poisson’s ratios, volume fraction index and Winkler, Pasternak elastic foundations. Foundation Parameters taken as:

$K_1=\raisebox{1ex}{$\left(k_1*D{D}_1\right)$}\!\left/ \!\raisebox{-1ex}{$\left(a^4\right)$}\right.$ ,$K_2=\raisebox{1ex}{$\left(k_2*D{D}_1\right)$}\!\left/ \!\raisebox{-1ex}{$\left(a^2\right)$}\right.$ , where $D{D}_1=\raisebox{1ex}{$\left(Ec*h_3\right)$}\!\left/ \!\raisebox{-1ex}{$\left(12*\left(1-V{c}_2\right)\right)$}\right.$ .

In the present study, the various combination of boundary edge support conditions namely, simply supported, clamped and two opposite edges are clamped and simply supported, the temperature of metal and ceramic are taken as T_c=600^°K,T_m=300^°K, with uniform temperature distribution. The boundary conditions can be written as

All edges simply supported (SSSS)

$v=w={\theta }_y={\psi }_y=0,atx=0,a;u=w={\theta }_x={\psi }_x=0aty=0,b$ ;

All edges clamped (CCCC):

$u=v=w={\psi }_x={\psi }_y={\theta }_x={\theta }_y=0,atx=0,aandy=0,b;$

Two opposite edges clamped and other two simply supported (CSCS):

$u=v=w={\psi }_x={\psi }_y={\theta }_x={\theta }_y=0,atx=0andy=0;$ ;

$v=w={\theta }_y={\psi }_y=0,atx=au=w={\theta }_x={\psi }_x=0,aty=b$

The dimensionless mean post buckling load of the FGM plate subjected to mechanical (${\lambda }_{cr}$ ) and thermal (${\lambda }_{Tcr}$ ) loadings is defined as respectively,²²

${\lambda }_{cr}=\frac{{(N^b{}_x)}_{cr}{b}^2}{E_c{h}^3}$ and ${\lambda }_{Tcr}=\lambda \alpha {(\Delta T)}_{cr}\times {10}^3$

Where,${(N^b{}_x)}_{cr}$ is dimensionalized critical post buckling mechanical and thermal of the FGM plate. The following temperature dependent [TID] material properties of functionally graded materials are given in Table 1.^36,38 The value of temperature T is taken as 300K for the analysis.

Validation study for mean buckling response

The comparisons of non-dimensional critical buckling loads obtained by the present theory and those given by Thai and Choi³⁸ & Reddy et al.⁴⁰ presented in Table 1 and observed the close agreement between the results. It can be seen that, in this loading condition also, the non-dimensional critical buckling load decreases with the increase of power-law index. Table 2 shows the comparison of critical buckling load $\left({{\displaystyle N}}_{cr}=\frac{{{\displaystyle N}}_{cr}{a}^2}{{\pi }^2{{\displaystyle D}}_0}\right)$ for a simply supported FGM plate with a/h = 100 and r/a = 0.2. The effective material properties are computed by rule of mixtures. In order to be consistent with the literature, the properties of the metallic phase is used for normalization T_c=400, T_m=300. a=50, b=50. S1 Quarter considering 9th & 81st nodes. It is clearly seen present [HSDT] results are in good agreement with Natarajan et al.³⁷ & Zhao.⁴³ Validation study of critical buckling temperature rise for square aluminum /alumina plate with uniform temperature rise and plate thickness ratio (a/h) = 20, a=50, b=50, a/b=1. T_c =600, T_m=300 is presented in Table 3. Again it can be seen that present HSDT results are in good agreement with the results of Wu et al.²² & Lal et al.⁴² The validation study of results using present outlined approach is compared with those available in literature through numerical examples. Figure 2 examines the comparison of dimensionless mean post buckling load, TID material properties of clamped supported square FGM plate subjected to mechanical loading with those of Wu et al.²² & Lal et al.⁴² various volume fraction index (n) and amplitude ratios (W_max/h). Clearly, it is seen that the present DISFEM results using HSDT are in good agreement with the available analytical results.

Validation study for stochastic post buckling response

The validation study for the COV of the initial buckling load due to randomness in material properties (b_i, (i=1,..., 4) for CCCC bi-axially compressed square Al/ZrO₂ plate with volume fraction index (n = 0.0 and 0.2) and a/h = 10, is shown in Figure 3 and compared with those published results of Yang et al.²⁸ & Lal et al.⁴² It can be seen that the present outlined approach [DISFEM] for different volume fraction index are in very good agreement with the results of Lal et al.⁴² & Yang et al.²⁸ using FSDT with semi-analytical approach in conjunction with FOPT. The comparison of probabilistic results obtained by DISFEM and independent MCS technique of square FGM plate without and with Winkler and Pasternak elastic foundations with simply supported boundary conditions in thermal environments and amplitude ratios, b/h=10 having random change in E_c material property keeping other as deterministic to their mean position is shown in Figure 4. For the MCS approach 10,000 random number based on convergence is used to simulate the results of desired mean and standard deviation (SD) using normal distribution function. From the figure, it is seen that present results obtained by DISFEM approach are very good agreements with the independent MCS approach.

Parametric study for second order statistics of post buckling response

Table 4 shows the effects of volume fraction index (n), amplitude ratios (W_max/h) and input random variables [b_i, (i =1,…, 7) = 0.10] on the dimensionless mean and COV, of thermally induced post buckling load and temperature of square geometrically nonlinear simple support FGM plate with TID material properties, Plate thickness ratio (a/h) =10. It is observed that expected mean post buckling load increases on increasing volume fraction index and simultaneously on increasing amplitude ratio. COV is varying different for different volume fraction index and amplitude ratio with combined effect of all input random variables. Effects of elastic foundations, volume fraction index (n), amplitude ratios (W_max/h) and input random variables [b_i, (i =1,…, 7) = 0.10] on the dimensionless mean and COV, of thermally induced post buckling load and temperature of square geometrically nonlinear simple support FGM plates resting on Winkler and Pasternak elastic foundations with TID material properties, Plate thickness ratio (a/h) =10 is presented in Table 5. It is seen that expected mean post buckling load increases on increasing volume fraction index and amplitude ratios with combined input random variables for both Winkler and Pasternak elastic foundations and more especially for Pasternak elastic foundations. However COV decreases much for Pasternak elastic foundations.

Table 6 shows the effects of plate thickness ratios (a/h) with types of loadings, volume fraction index (n), amplitude ratios (Wmax/h) and input random variables [bi, (i =1,…, 7) = 0.10] on the dimensionless mean and COV, of thermally induced post buckling load and temperature of square geometrically nonlinear simple support FGM plate with TID material properties. It is noticed that expected mean post buckling load decreases on increasing plate thickness ratio, volume fraction index and amplitude ratios with combined input random variables, whereas the COV decreases in same conditions. Amplitude ratios are noticeable for thin plates. Effects of elastic foundations, plate thickness ratios (a/h) with types of loadings, volume fraction index (n), amplitude ratios (Wmax/h) and input random variables [bi, (i =1,…, 7) = 0.10] on the dimensionless mean and COV, of thermally induced post buckling load and temperature of square geometrically nonlinear simple support FGM plates resting on Winkler and Pasternak elastic foundations with TID material properties is presented in Table 7. It is observed that the plate thickness ratios, combined effects of input random variables and amplitude ratios with volume fraction index significantly affect the expected mean post buckling load for both Winkler and Pasternak elastic foundations. For same conditions the COV is much affected for Pasternak elastic foundations compared to Winkler elastic foundations. Table 8 shows the effects of plate aspect ratios (a/b), volume fraction (n), amplitude ratios (Wmax/h) and input random variables [bi, (i =1,…, 7) = 0.10] on the dimensionless mean post buckling load and COV, of thermally induced post buckling load and temperature square geometrically nonlinear simple support FGM plate with TID material properties. a/h=20. It is noticed that for square plates when there is increase of volume fraction index, combined input random variables and amplitude ratios, the post buckling load decreases and COV increases. For rectangular plates the post buckling load further increases and COV decreases on increasing volume fraction index. Effects of elastic foundations, plate aspect ratios (b/a), volume fraction (n), amplitude ratios (Wmax/h) and input random variables [bi, (i =1,…, 7) = 0.10] on the dimensionless mean and COV, of thermally induced post buckling load and temperature square geometrically nonlinear simple support FGM plates resting on Winkler and Pasternak elastic foundations with TID material properties. a/h=20 is presented in Table 9. It is noticed that for given volume fraction index, amplitude ratios (Wmax/h) and input random variables the mean post buckling load increase and COV decrease for square plates, however the post buckling load and COV is higher when plate is resting on Pasternak elastic foundations compared to Winkler elastic foundations. On changing aspect ratios for rectangular plates post buckling load and COV further increase for given conditions. Table 10 shows the effects of various support conditions, volume fraction (n), amplitude ratios (Wmax/h) and input random variables [bi, (i =1,…, 7) = 0.10] on the dimensionless mean and COV, of thermally induced post buckling load and temperature square geometrically nonlinear simple support FGM plates with TID material properties, a/h=30. It is observed that for SSSS support plates increase in volume fraction index, amplitude ratios and input random variables the post buckling load decreases and COV increases. But when plates are CSCS and CCCC support the mean post buckling load further increase; however there is marginally decrease in COV. SSSS support is superior to CCCC and CSCS support. Effects of elastic foundations, various support conditions, volume fraction (n), amplitude ratios (Wmax/h) and input random variables [bi, (i =1,…, 7) = 0.10] on the dimensionless mean and COV, of thermally induced post buckling load and temperature square geometrically nonlinear simple support FGM plate resting on Winkler and Pasternak elastic foundations with TID material properties, a/h=30 is presented in Table 11. It is noticed that for given SSSS support conditions, volume fraction index, amplitude ratios and combined input random variables the mean post buckling load e decreases and COV increase for both Winkler and Pasternak elastic foundations support conditions; however the values are more significant for Pasternak elastic foundations support conditions. But when same plates are CSCS and CCCC the mean post buckling load further increases and COV decreases. Post buckling load and COV are higher for Pasternak elastic foundations. Table 12 shows the effects of material properties with volume fraction index (n), amplitude ratios (Wmax/h) and input random variables bi, [(i =1,…, 7)=0.10] on the dimensionless mean and COV, of post buckling load and temperature square geometrically nonlinear simple support FGM plates with TD material properties., a/h=20. It is noticed that on increasing volume fraction index and amplitude ratios with input random variables the mean post buckling load decreases and there is marginal increase in COV for given conditions. But on changing plate material there is significant decrease in mean post buckling load and increase in COV at similar conditions. The effects of material properties with volume fraction index (n), amplitude ratios (Wmax/h) and input random variables bi, [(i =1,…, 7) =0.10] on the dimensionless mean and COV of post buckling load and temperature square geometrically nonlinear simple support FGM plates resting on Winkler and Pasternak elastic foundations with TD material properties., a/h=20 is presented in Table 13. It is noticed that on increasing volume fraction index, amplitude ratios with input random variables the mean post buckling load change for Winkler foundations and they further increase for Pasternak elastic foundations; however the COV decreases and in more for Pasternak foundations. On changing plate material for same conditions the mean post buckling load further decrease and COV is higher for plates resting on Pasternak elastic foundations.

Figure 1 Geometry of Functionally graded material plate.

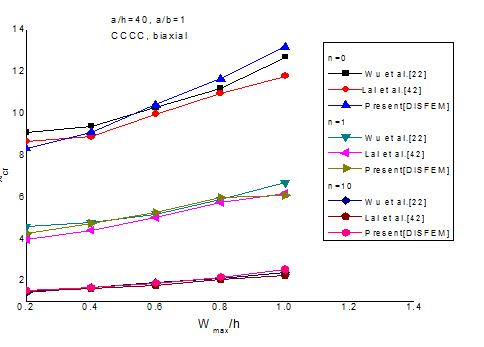
Figure 2 The validation study for the mean of the initial buckling load.

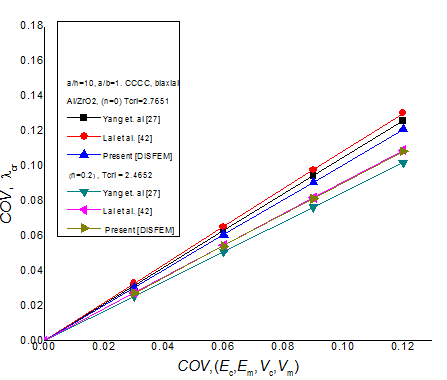
Figure 3 The validation study for the COV of the initial buckling load due to randomness in material properties.

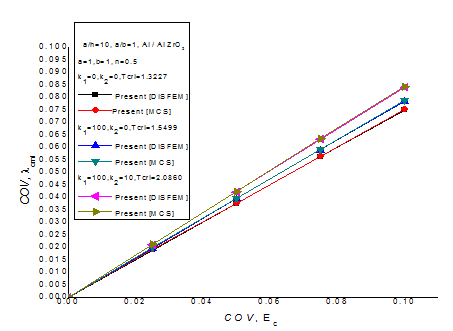
Figure 4 Validation study for COV, random material property Ec.