Sun sensors are commonly employed to determine the attitude of a spacecraft by defining the unit sun vector, which points from the center of the spacecraft's local reference frame toward the center of the sun. That information can then be used to satisfy the pointing requirements of an attitude control system, such as the one to be implemented on the SpudNik-1 CubeSat; this system requires knowledge of attitude to within 0.13 degrees, making high-accuracy sun sensors a necessity. However, like most off-the-shelf space hardware, commercially available high-accuracy sun sensors are expensive, making it difficult for teams working on space projects to both meet their pointing requirements and comply with their financial constraints.

The purpose of this research is to assess the concept of using a simple pin-hole camera as a low-cost high-accuracy sun sensor for CubeSat application. To do so, an off-the-shelf camera module, which employs an OV7670 image sensor, was modified to replace the lens with a small hole before fixing it to the base of a robotic arm. The robotic arm was then programmed to point a laser attachment toward the hole while changing the angle of incidence in 1 degree increments. Due to the high intensity of the laser, the image sensor needed a brief period of about 5 seconds to reach steady-state after each movement. As a result, a series of images were taken for each position and images were only selected for further processing once their visible change with respect to time was minimal. Once the data was gathered, a MATLAB script was written to process the images and determine the laser's angle of incidence based on the sensor's geometry.

Provided that the sensor is used within its region of operation, which is limited by its field-of-view of about 8 degrees, the results from this test show that a maximum error of 0.09 degrees was achieved when compared to the angle input given to the robotic arm; note that the robotic arm has an expected error of about 0.003 degrees. Otherwise, when the sensor is used outside its region of operation, data gets lost as the laser begins to leave the active area of the sensor; this causes the accuracy to decline gradually until the laser cannot be detected at all. These results show that the mock-up pinhole camera can meet the stringent accuracy requirement for attitude knowledge on the SpudNik-1 CubeSat. Further research is to be conducted into enhancing this design.

Sun sensors are commonly employed to determine the attitude of a spacecraft by defining the unit sun vector, which points from the center of the spacecraft's local reference frame toward the center of the sun. To do so, they use photosensitive elements, which measure the angles at which incoming sunlight contacts the sensor. Using the placement geometry of the sensor, these angles can be related to those at which the spacecraft's body frame is positioned about it's local frame; these relations can then be used in combination with an orbital model to define the spacecraft's attitude with respect to the planet being orbited.¹ Note that multiple sensors are required in order to required to fully define the orientation of the body frame and are often used to widen the field-of-view. Once the unit sun vector has been defined, it can then be used as feedback to satisfy the pointing requirements of an attitude control system.

There are many different types of sun sensors; these are often classified by: the number of axes that the sensor can detect angles about, the type of output signal, and the measurement principle. In general, sun sensors are either one-or two-axis and have either analog or digital output signals. A common measurement principle uses the spatial relations between one or more sunlight-permeable slits and an array of photosensitive elements;² assuming that the sun is within the field-of-view of the sensor, sunlight will then land on specific elements depending on the angle(s) at which it passes through the slit(s). As a result, the angle(s) can then be measured using the readings of the photosensitive elements and the sensor's geometry. Many variations of this design exist, including those which replace the slits with a small hole or replace the photodiode array with either an image sensor³ or a position-sensitive detector (PSD).⁴

Another method is to use either the spacecraft's solar cells,^1,2 or stand-alone photodiodes that are mounted to the outer surfaces of the spacecraft; the angle of elevation between the photosensitive surface of these elements and the sun vector can then be correlated to the magnitude of the generated photocurrent. Sensors that make use of this method are typically labeled as “coarse” due to their relatively low accuracy where those which employ the previous method are typically labeled as “fine.”

High-resolution imaging satellites often have mission objectives which require high-accuracy attitude determination; in particular, the SpudNik-1 CubeSat being developed at the University of Prince Edward Island requires attitude knowledge to within 0.13 degrees, making high-accuracy sun sensors a necessity. However, like most off-the-shelf space hardware, commercially available fine sun sensors are expensive, making it difficult for teams working on space projects to both meet the pointing requirements of their spacecrafts and comply to their financial constraints.

The purpose of this research, similar to that in,³ is to assess the concept of using a simple pinhole camera as a low-cost high-accuracy sun sensor for CubeSat application. However, in contrast to,³ this research uses a low-fidelity model to both get an idea of what the worst-case performance would be and examine the impact that imperfections in the design would have on the results. A pinhole camera is the variation of the first measurement principle where the slit is replaced with a small hole and the photodiode array is replaced with an image sensor. In this variation, the hole is placed directly above the centroid of an image sensor's active area, allowing the sunlight's angle of incidence to be measured using the propagation of a light spot across the sensor's pixels; this concept can be seen illustrated in Figure 1.

Figure 1 Diagram of a pinhole camera.

Using basic trigonometry, it can be determined that the governing equation for this concept would be as follows:

${\theta }_i=arctan\left(\frac{x}{d}\right)$     (1)

Where θ_i is the angle of incidence; x is the position at which the sunlight contacts the image sensor, relative to the centroid of the active area; and d is the distance between the hole and the image sensor. Being as the active area of an image sensor is two-dimensional, this equation can be expanded to include the position along both the height and the width of the area; this will provide information on two angles of incidence, which can then be used to define a three-dimensional vector. Note that since the active area has finite dimensions, the sensor will have a field-of-view less than 180 degrees. The sensor's theoretical field-of-view can be determined through the following equation:

${\theta }_{FOV}=2arctan\left(\frac{x}{2d}\right)$     (2)

Where x is either the height or width of the image sensor's active area, depending on which angle of incidence is being examined.

For the experiment, an off-the-shelf camera module was selected mainly for it's availability and low-cost. The module employs an OV7670⁵ image sensor that features a 640 x 480 pixel active area where each pixel is 3.6 µm square. The module also had a built-in lens which was removed such that light could to access the sensor directly, rather than being altered by the optics. By doing so, a circular casing was left around the image sensor; this casing was measured to be about 10 mm from the surface of the camera module's printed circuit board. Once the lens was removed, the module was mounted to a small box which measured about 15 x 15 x 7.5 cm such that jumper wires could be easily connected to the camera module. A piece of black PVC tape was then pulled taut over the casing that surrounded the image sensor and adhered to the box in order to keep unwanted light out of the system; a pin of about 0.5 mm diameter was used to puncture a small hole in the tape such that the resulting hole lied roughly above the center of the image sensor's active area. The camera module was then wired to an Arduino Nano using a breadboard, resistors, and jumper wires as shown in Figure 2. The assembly layout is depicted in Figure 3.

Figure 2 Electrical interfacing diagram (my-botic n.d.).

Figure 3 Layout of the sun sensor assembly.

Once the sun sensor was assembled, it was fixed to the workstation of a FANUC LR Mate 200iD/7C robotic arm. To do so, the box that the sensor was mounted to was placed into a form-fitting cardboard cut-out. The cut-out was fixed to the workstation using masking tape such that the x and y axes of the sun sensor's reference frame would run parallel with those of the workstation's reference frame as can be seen in Figure 4; note that the origin of the sun sensor's reference frame is positioned at the center of the hole that was made in the tape and that the x-axis runs parallel with the image sensor's columns where the y-axis runs parallel with the rows. A picture of the set-up can be seen in Figure 5.

Figure 4 Reference frames within the experimental set-up.

Figure 5 Experimental set-up showing the robotic arm, the sensor mounted to the work-station, and the computer.

In order to simulate the sun, the robotic arm was equipped with it's laser-pointing end-effector. Note that while the sun is best represented as a point source of light, and could be better simulated using a wide angle LED, the highly collimated laser is still expected to produce accurate results due to the large distance between low-earth-orbit (LEO) and the sun, being as this distance is so vast, any of the sun’s rays that manage to enter the ~0.5 mm diameter pinhole are expected to have a high degree of parallelism. Being as the end-effector emits the laser in the -z direction of the tool frame, the z-axis of the tool frame was aligned with that of the sun sensor's frame; this centered the laser's spot on the hole in the PVC tape. The z-distance between the two frames was then measured and the robotic arm's software was altered to extend the z-distance between frame 4 and the tool frame by this amount, doing so essentially merged the tool frame with the sun sensor frame; while the distance did need to be tweaked through some trial and error, this allowed the robotic arm to change the laser's angle of incidence while maintaining the position of the laser's spot by revolving the end-effector about the y-axis of the tool frame.

Once the robotic arm was configured, third-party software was then installed on both the Arduino and a computer. The Arduino's software was used to continuously read the image sensor and transmit the data through a serial interface where the computer's software was used to monitor that serial interface and save the received data to a bitmap image file. After setting up the electronics for image capture, the laser attachment was revolved about the y-axis of the tool frame until the images received from the image sensor indicated that the laser's spot could no longer be seen; this corresponded to a -10.85 degree rotation. The data for the experiment could then be collected by incrementing the angle by 1 degree until the image sensor's data indicated that spot had translated across the height of the active area, which happened at 8.15 degrees; this gave a total of 20 positions.

However, it should be noted that due to the high intensity of the laser, the image sensor needed a brief period of about 5 seconds to reach steady-state after each movement. As a result, a series of images were taken for each position and images were only selected for further processing once their visible change with respect to time was minimal.

After obtaining the data, a MATLAB script was then written to find the centroid of the laser's spot and use the geometry of the prototype sun sensor to transform this value into an angle of incidence. To do so, the script first

applies a mask to transform the grey scale image into a binary image. While experimenting, it was found that accuracy of the results increased with an increased threshold for a pixel's depth to qualify as a white pixel. Hence, the results to be shown in this paper will correspond to a threshold which corresponds to 99% of the maximum pixel depth. After creating the masked images the script finds the centroid of the spot using a weighted average as depicted in Equation 3,

$R=\frac{{\displaystyle \sum _{j=1}^{n_{row}}\left(j\ast \left({\displaystyle \sum _{i=1}^{n_{col}}\left(p_{j,i}\right)}\right)\right)}}{p_{total}}$     (3)

Where R is the row at which the centroid lies, n_row and n_col are the number of rows and columns respectively, p_j,i is the value of the pixel at row j and column i, and p_total is the sum of all pixel values. Once the average row is computed, it then gets converted to a displacement from the center row of the image sensor such that the angle of incidence can be calculated as shown in Equation 1. Note that the angle calculation requires the distance between the hole and the image sensor; this was approximated to be 9.055 mm using the height measurement of the housing around the image sensor and the dimensions found in sensor's datasheet.

Three different methods were used in order to determine the displacement from the image sensor's center row, each more accurate than its predecessor; the first and second methods, which are referred to as the "Single Pixel Row" and "Double Pixel Row" methods, are further detailed in Appendix A. Each of the three methods use the image height of 320 pixels to define the center of the sensor as being located between rows 160 and 161. However, unlike the first method, the final method, referred to as the “Double Pixel Row With Off-Set Correction" method, accounts for the difference between the image height and the active area's 640pixel height by defining the image's pixels to be twice that of the 3.6 µm pixel height specified in the sensor's datasheet. This method also corrects for an offset, which is believed to be caused by the pinhole not being directly above the centroid of the image sensor's active area; it does so by mapping the average row of the image corresponding to 0.15 degrees such that the sensor output will be the expected value, rather than mapping the center row to 0 degrees. The final equation can be seen as Equation 4, the results generated by using this function are compared to compared to the robotic arm's position in Figure 7 and to the other two methods in Figure 9.

Figure 6 Images generated during the experiment.

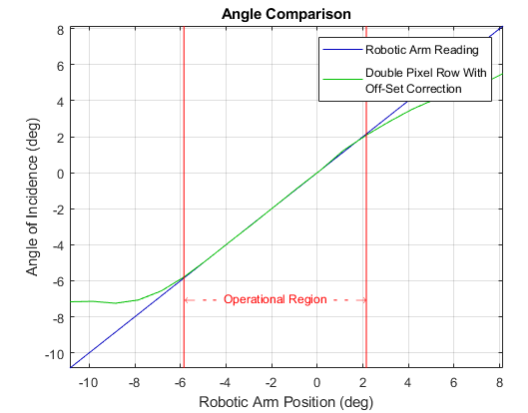
Figure 7 Angle comparisons between robotic arm input and "Double Pixel Row with O-Set Correction" algorithm.

$x=0.0072r-1.3383$     (4)

Where x is displacement along the height of the image sensor and r is the average row.

The selected images can be seen in Figure 6; As to be expected, they show that the laser's spot traversed the height of the active area. Note, however, that there is significant data loss in images where the laser's spot approaches the edges of the active area. As a result, it is necessary to define a region in which the data is sufficient; this has been labeled as the “operational region."

Figure 7 illustrates the results from each of the three methods as well as the angles given as input to the robotic arm. Figure 8, which displays the absolute error given by each image, was used to define the operational region; this was done by selecting all of the data that fell within the ~0.13 degree accuracy requirement of the SpudNik-1 CubeSat. The result was that the region spanned from the -5.85 degree position to the 2.15 degree position, looking at the absolute error within this region, it can be seen that the maximum is about 0.09 degrees.

Figure 8 Absolute error between robotic arm input and the "Double Pixel Row with O-Set Correction" algorithm.

Looking at the results, it can be seen that the sensor appears to be well within the ~0.13 degree accuracy requirement set by the attitude determination system of the SpudNik-1 CubeSat. In terms of accuracy, this is very comparable to commercial high-accuracy sun sensors; as examples, the accuracy rating of the NSS series and nanoSSOC-D60 sensors range from 0.5 degrees to 0.1 degrees.^6,7 Note, however, that there is a relatively large spike of error at 1.15 degree position; the reason for this is currently unknown as the image does not appear to have any abnormalities, but it does pose the question of whether or not there were enough sample points taken. While the results of this experiment do seem promising in terms of the sensor's accuracy meeting that required by SpudNik-1's attitude determination system, there are two other factors which should be drawn attention to: the field-of-view, and the fact that the operational region is non-symmetrical about the 0 degree reading.

Firstly, the operational region suggests that the sensor's field-of-view would only be about 8 degrees; comparing this with the NSS series and nanoSSOC-D60 sensors, which are rated for 114 and 120 degrees respectively,^6,7 this specific prototype simply does not compare. Note, however, that there are ways to increase the field-of-view of this sensor. One method of doing so falls from the fact that the theoretical field-of-view, which can be determined through Equation 2 to be just 14.501 degrees, is significantly larger than what was shown in the results; this is because the equation assumes that the entire active area can be used for detecting the angle. Yet, as discussed in the previous section, the results show that only a portion of the sensor, depicted by the "operational region," can be used to accurately measure the angle; this means that there is a potential to increase the field-of-view by improving the software to recognize when the spot is approaching the edge of the sensor, and correct for the lost data.

Equation 2 also shows that the field-of-view can be increased by either reducing the distance between the hole and the image sensor, or increasing the height of the image sensor's active area. Assuming that a distance of 2 mm between in the hole and the image sensor is achievable, then the theoretical field-of-view of the current prototype could be increased to about 59.883 degrees; taking this one step further and decreasing the distance to 1 mm could increase the field-of-view up to about 98.080 degrees. On the other hand, if the distance between the hole and the image sensor is kept at 9.055 mm and a larger image sensor is used, such as a Python 5000 which has an active area of about 12.4416 mm x 9.8304 mm, then the field-of-view could be increased up to 68.978 degrees for the longer side of the sensor or 56.988 degrees for the shorter side. Combining the 1 mm spacing with the Python 5000 image sensor could get up to a 161.736 degree field-of-view. Other ways of increasing the field-of-view would also include the addition of an aspheric lens to bend the light toward the center of the image sensor, or to use additional sensors angled in a strategic manner.

Although there are many methods of increasing the field-of-view, it should be noted that most of them will have an effect on the resolution of the sensor and some may decrease resolution to a point where the required pointing accuracy cannot be achieved. Methods such as decreasing the height or implementing an aspheric lens will alter the change of the spot's displacement along the active area with respect to a change in the angle, a decrease in this value would correspondingly decrease the resolution. Other methods replace the sensing element altogether, if it is replaced by a different image sensor or another type of digital sensor, then an increase in element size from 7.2 µm would also decrease the resolution; however, if it is replaced by an analog sensor, such as a PSD, then the resolution would depend on the noise characteristics and the resolution of the analog to digital converter.

As for the non-symmetrical operational region, it can be seen in Figure 9 that the "Double Pixel Row" plot has a more symmetrical operational region than the "Double Pixel Row With Off-Set Correction" plot; the former ranges from -4.65 degrees to 3.24 degrees where the latter ranges from -5.7954 degrees to 2.0857 degrees. This is thought to be caused by the pinhole not being directly above the centroid of the sensor's active area as the only difference in the methods used to generate these plots is a remapping which is believed to correct for this.

Figure 9 Angle comparison between robotic arm input and sensing algorithms.

In combination with the pinhole's offset, it is also possible that more error spikes, such as the one at the 1.15 degree position, may have caused some additional asymmetry.

While this research suggests that a simple pin-hole camera can achieve accuracy comparable to that of high-accuracy sun sensors, it lacks an investigation into whether or not supplementary requirements of an attitude determination system, such as the field-of-view, can be achieved concurrently. As a result, further research is to be conducted which will aim to: improve the field-of-view by implementing multiple sensors which have both a larger active area and less distance between that and the hole; increase the precision of where the hole is placed through additive manufacturing; and simplify both the electrical interfacing and software by implementing a position sensitive device (PSD), rather than an image sensor.

None.

Authors declare that there is no conflict of interest.

The first method uses the 320 pixel height of each image and the 3.6 µm height of each pixel on the image sensor. From the image height, it can be determined that the center row would occur between rows 160 and 161. It is then assumed that each pixel in the received image corresponds to one pixel on the image sensor. As a result, the transfer function from row number to displacement was defined as a linear scaling function which equates to 0 at a row number of 160.5 and 0.0018 mm at a row number of 161; this function is shown in Equation 5 and produces the results shown by the “Single Pixel Row" plot in Figure 9. The other two methods will be discussed in the upcoming section.

x = 0:0036r – 0.5778 (5)

When looking within the operational region, it can be seen that the first method has a linear trend similar to that of the input given to the robotic arm, but it is obvious that the slope of this trend is much more gradual; for this reason, the function which maps from row number to displacement was revisited. Upon realizing that the active area of the sensor actually had a height of 640 pixels, despite the fact that the images had a height of 320 pixels, it was discovered that the third-party software effectively merged every second row with it's predecessor, contradicting the initial assumption that each pixel in the received image corresponds to one pixel on the image sensor. As a result, the function was adapted such that the pixel size was doubled, meaning that a row number of 161 would instead map to a displacement of 0.0036 mm. The updated transfer function can be seen in Equation 6 and its results are shown by the “Double Pixel Row" plot in Figure 9.

x = 0:0072r – 1.1556 (6)

1. Gaebler J. Coarse Sun Sensing for Attitude Determination of a CubeSat. B.S. Thesis: Florida, USA; 2007.
2. Post MA, Junquan Li, Regina Lee. A Low-Cost Photodiode Sun Sensor for CubeSat and Planetary Microrover. International Journal of Aerospace Engineering. 2013;2013:549080.
3. Antonello A, Lorenzo O, Alessandro F. Development of a low-cost sun sensor for nanosatellites. Acta Astronautica. 2018;144:429-436.
4. Rodrigues PM, Pedro MR. Design and characterization of a Sun Sensor for the SSETI-ESEO Project. In: XVIII IMEKO World Congress; 2006.
5. Mybotic (n.d.). OV7670 Arduino Camera Sensor Module Framecapture Tutorial.
6. Sun Sensor (n.d.). NSS. Ver. 7b. NewSpace Systems.
7. Sun Sensor for Nano-Satellites Digital Interface. nanoSSOC-D60. Ver. 1.08. SolarMEMS; 2016. 23 p.