Seismic wave velocities, including effective velocities, play a critical role in the kinematic processing and interpretation of 2D and 3D seismic data. Along with other parameters of elastic waves, the geological efficiency of seismic exploration also depends on the level of knowledge of the velocity model of the medium, on the accuracy of information about velocities. The article briefly lists the main methods for determining the effective velocities according to the seismic wave field, developed and applied in the practice of seismic research. The methods used to determine the effective velocities of reflected waves can be divided into two groups: methods for determining the effective velocities based on automatic or visual tracking of the in-phase axes (i.e. hodographs) of reflected waves on seismic records, then their approximation by hyperbolas constitute the first group, and the second the group consists of methods based on the application of the analysis of the seismic wave field in controlled directions on the seismograms of a common depth point (CDP). Each proposed method for determining effective speeds has advantages and disadvantages. The article focuses on the industrial method, widely used at present, based on the analysis of the wave field in controlled directions, which do not provide sufficient information to solve the main problems of kinematic interpretation. The main disadvantages of the existing methods are indicated.

The article describes a new method for determining the effective velocity, which is fundamentally different from the methods that are still used in the practice of seismic exploration. The fact is that in this method, seismic survey data of single and multiple profiling are not used separately, as it was in the methods used in seismic survey practice so far, but together. Formulas have been derived for determining the effective velocity based on the time gradients of the travel time curves of the CSP and CDP of reflected waves, which makes it possible to determine the speeds even from incomplete travel time curves. A technique for determining the effective speed has been developed and a sequence of procedures has been determined for solving the problem. The results of research are given on a specific example by solving the direct and inverse problems for the Sazhdag area between the Kura and Gabyrra rivers. The influence of errors in the values of the parameters included in the formula for calculating the effective speed on the final results is studied. At the end of the article, the main advantages of the proposed method are indicated.

Keywords: 2D and 3D seismic, effective velocity, common depth point velocity, time increments, seismic time sections

Seismic wave velocities, used in the practice of seismic work, being an important parameter, are used in solving a number of geological problems assigned to 2D and 3D seismic surveys. Inaccuracies in the determination in the velocity model of the medium, as well as incomplete information about velocities lead to a decrease in the geological efficiency of seismic exploration. Over the entire period of application of seismic exploration in the search and exploration of minerals, various researchers have proposed and applied different methods for determining effective velocities from seismic records. Among which, the works of A.V. Vasilev and A.K. Urupov,^1,2 V. M. Glogovsky³ and G. N. Gogonenkov,⁵ A. V. Nevinny⁵ and A. K. Urupov,⁶ N.N. Puzyrev,⁷ A.K. Urupov and A.N. Levin⁸ R.A. Abdullaev, and others determined by sum optimization.

Used in practice algorithms for determining based on CDP (or CMP) seismograms are based on the assumption of the validity of approximating CDP (or CMP) travel time curves - a common midpoint in 3D seismic surveys) by hyperbolas.^4–6 We know that in complex surface and deep seismo-geological conditions, the travel time curves of reflected waves often do not have a hyperbolic shape: cusps, nodes, etc. are formed on them, which leads them to an unsuitable shape for determining the stacking velocity.^9–11 At present, the most technological way to determine the speeds, since the beginning of the use of CDP (common depth point method) are the stacking rates (or CDP) obtained by digital data processing.^12,13

As it became clear that the velocities determined on the basis of the analysis of the observed wave field in controlled directions are the main source of information about the effective velocities at present. For given seismogeological conditions and with the optimality of the previous processing, the information content and accuracy of calculations (i.e., velocity analysis) depend on the width of the analysis time window, the hyperbolicity of the hodograph and its length, in addition, this method, based on sum optimization, is in practice carried out at several points of the profile, and linear interpolation is performed between them. Moreover, it is also necessary to recalculate the summation rates into effective rates, i.e. take into account the influence of the tilt angle of the reflecting boundary on the CDP velocity.^14,15 Manual or digital seismic migration using the method of averages gives only an approximate picture of the real geological environment, since refractions of seismic rays at intermediate interfaces are not taken into account. And obtaining migrated depth sections requires accurate knowledge of the velocity model among, it is known that this procedure is very sensitive to velocity changes.^16,17 Thus, it is clear.

Our department has developed a new method for determining the effective velocity, which differs significantly from the methods that are still used in the practice of seismic exploration. In this method, data from single and multiple profiling records are used together to determine effective rates.

Let us take the equation of the travel time curve of the CTV (common explosion point) of the reflected wave, differentiate it with respect to x, and obtain an expression for the time gradient:

$\frac{dt}{dx}=\frac{x}{{\upsilon }^{2}t}\pm \frac{2h\sin \varphi }{{\upsilon }^{2}t}$   (1)

Above the origin, which is usually above the source of seismic waves, the expression for the time gradient is much simpler, since at x=0 the time, $t=t_0=\frac{2h}{\upsilon }$  and the first term in (1) is equal to zero $\frac{x}{{\upsilon }^{2}t}$ = 0 and the expression for the time gradient, with some assumptions, takes the following rather simple form:

${\left(\frac{dt}{dx}\right)}_0=\pm \frac{\sin \phi }{\upsilon }$   (2)

Considering that when determining effective seismic wave velocities, only the absolute values of the time gradients matter, we omit the signs on the right side of expression (2) and for find:

$\sin \varphi =\upsilon \cdot {\left(\frac{dt}{dx}\right)}_0$   (3)

Let's move on to the second part of the problem and differentiate the equation of the CDP hodograph of the reflected wave with respect to x and obtain the following expression for:${\left(\frac{dt}{dx}\right)}_{ОГТ}$

${\left(\frac{dt}{dx}\right)}_{ОГТ}=\frac{x}{{\upsilon }_{ОГТ}^2\cdot t_{ОГТ}}$   (4),

Znaeat that${\upsilon }_{ОГТ}{}_{Ђн}=\frac{\upsilon }{\cos \varphi }$ , we use the expression known from trigonometry and substitute instead of $\cos \phi =\sqrt{1-}{\sin }_{}^2\phi$ expression (3), for the effective speed we obtain:

${\upsilon }_{Эф}=\sqrt{\frac{X}{{\left(\frac{dt}{dx}\right)}_{ОГТ}\cdot t_{ОГТ}+X\cdot {\left(\frac{dt}{dx}\right)}_0^2}}$

Naturally, the use in calculations instead of the time gradient of the time incrementbased on reception makes calculations easier and more convenient, and the use of the time increment does not introduce large errors. Naturally, the choice of valuedepends on the curvature of the front of the reflected wave, and it is known that with increasing time the curvature of the hodograph decreases, it becomes flatter, and the basis for determining the velocity can be increased. Based on all that has been said, to determine the effective speed, we obtain the following expression:

${\upsilon }_{ef}=\sqrt{\frac{X_m}{{\left(\frac{\Delta t}{\Delta x}\right)}_{ОГТ}\cdot t_{ОГТ}+X_m{\left(\frac{\Delta t}{\Delta x}\right)}_0^2}}$   (5)

Here ${\left(\frac{\Delta t}{\Delta x}\right)}_{ОГТ}$ time increment according to the CDP hodograph at the base, the center of which is located at a distance Xm from the origin; ${\left(\frac{\Delta t}{\Delta x}\right)}_0$ time increment according to the OTV hodograph on the same base $\Delta x$ , the center of which is at the origin; $t_{ОГТ}$ time on the CDP hodograph for Xm abscissa.

The effective velocity is determined in the following sequence: two parameters are selected and set by the geophysicist (Хm and $\Delta x$ ) included in the expression (5) and the observed wave field determines the time increments on the selected base ${\left(\frac{\Delta t}{\Delta x}\right)}_0$ and ${\left(\frac{\Delta t}{\Delta x}\right)}_{ОГТ}$ , as well as on the CDP hodograph for the Xm abscissa. An analysis of the shape of the CDP hodograph of the reflected wave, as well as the practice of calculations show that it is advisable to choose the abscissa Xm at remote distances from the origin of coordinates, since at these offsets, the hodograph asymptotically approaches a straight line. For example, if the reception spacing length is 2.35 km, then Xm = 2.15 km. What about $t_{ОГТ}$ $\Delta x$ , then the choice of the value of this parameter plays a big role in the accuracy of determining the speed, since if it’s very small value leads to an incorrect determination of time increments under the influence of irregularly distributed factors (for example, such as zones of low velocities, relief, residual static corrections, inhomogeneity of the overburden, etc.), then its large value is limited by the curvature of the front waves, which is essential at short registration times. Experience shows that for a medium differentiated section at registration times of more than 1.5 sec $\Delta x$ can be increased to 0.4 km. When determining the reflected wave from the CDP hodograph, two methods can be used: the first method consists of summing seismograms along an adjustable fan of hyperbolic hodographs, the second, simpler method uses velocity analysis data, using its data to determine the time in the center of the base, setting the abscissa of the edges of the base x1 and x2 times, as well as its increment on this base.

As for the time gradient (i.e. time increment based on ∆х) determined by the hodograph of the ITV at the origin of coordinates ${\left(\frac{\Delta t}{\Delta x}\right)}_0$ , then this parameter can be determined by the method of controlled directional reception (MRNP) L.A. Ryabinkin, for the use of which in the digital processing of seismic data, algorithms and programs were developed and applied back in the mid-80s of the last century [L.A. Ryabinkin, 1987].

Let us consider a practical example of calculating the effective velocity for a simple model of one of the areas located to the northwest of the Mingechevir reservoir in Azerbaijan. Let us first solve the direct problem, i.e. for a simplified model of the environment of the Sazhdag area between the Kura and Gabyrra rivers of Azerbaijan, we calculate the travel time curves of the CSP and CDP of reflected waves for the interfaces located at different depths. For calculations, we use seismic logging data from well No. 4 of the Sazhdag area (Figure 1). To compare the results, we calculate the hodographs for two depths: 1) h = 1.0 km; $\upsilon =2,3$ km/sec; 2) h = 4.0 km, $\upsilon$ = 2.6 km/sec; the calculations were carried out for an inclined reflecting boundary with an inclination angle $\phi$ =200 and for horizontal border $\phi$ =00, and the length of the hodographs is taken equal to 2.4 km.

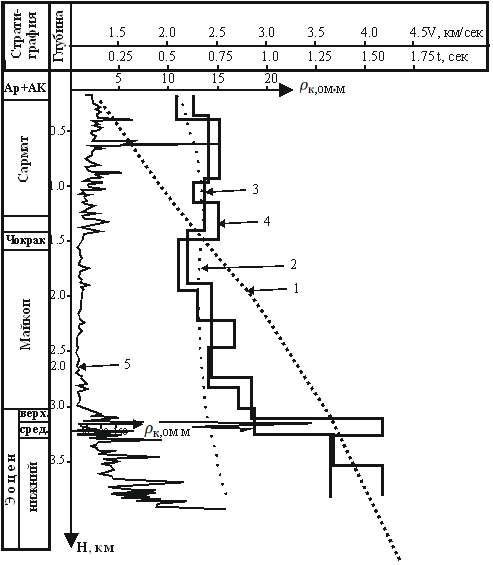
Figure 1 Curves of electric and seismic logging, well No. 4 of the Sazhdag area of the Kura and Gabyrra Mesopotamia.
1-vertical hodograph; 2-average speed curve; 3- formation velocities; 4-interval speeds; 5-curve of apparent electrical resistance

The calculated and constructed hodographs are shown in Figure 2.

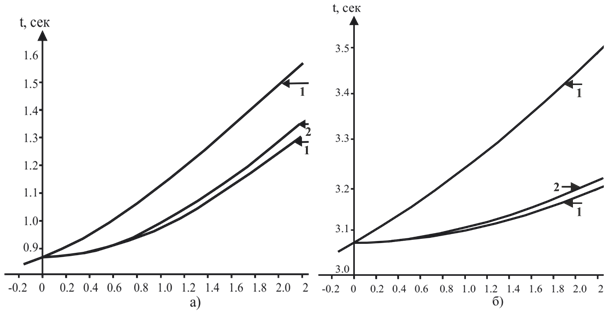
Figure 2 Travel time curves of the CSP and CDP of reflected waves calculated from the seismic logging data of well No. 4: travel time curves at: a - h = 1.0 km and b - 4.0 km; 1 - hodographs of OTV and CDP (at ); 2 - hodographs of the OTV and CDP (at ); $\phi = {20}^0\phi = 0^0$

The resulting hodographs are used to calculate effective velocities $\upsilon$ ef, i.e. let’s solve the inverse problem using the calculated travel time curves of the CTV and CDP. Let us assume that Хm=2.15 km, then at the point Хm = 1.236 sec (at h = 1.0 km) = 3.174 sec (at h = 4.0 km). At these depths (h = 1.0 and 4.0 km), the time gradients on the ODW and CDP hodographs will be equal, respectively: ${\left(\frac{\Delta t}{\Delta x}\right)}_0$ = 0.184 sec/km (h = 1.0 km) and 0.135 sec/km (h = 4.0 km), = 0.29 sec/km (h = 1.0 km) and 0.088 sec/km (h = 4.0 km). Substituting the values of these parameters in expression (5) in place, for the effective speed at different depths we obtain the following values: at h = 1.0 km, $\upsilon$ ef= 2.301 km/s, and at h = 4.0 km, $\upsilon$ ef= 2.608 km/sec. If we compare the values of effective velocities obtained from the hodographs with the initial data, we will see that, with the exception of small errors, they completely coincide.

In the calculations, errors may be made in the values of the parameters included in the formula for calculating the effective speed and their influence on the final results, we will investigate possible errors. We can definitely say that when determining Xm, it is impossible to make significant errors. Instead of time, let's take and define time gradient ${\left(\frac{\Delta t}{\Delta x}\right)}_0$ and ${\left(\frac{\Delta t}{\Delta x}\right)}_{ОГТ}$ without taking into account the curvature of the wave front according to the full travel time curves of the CTV and CDP. In the practice of seismic research, flank observation systems are widely used and, in this regard, the determination of the time gradient on the base, the center of which is located above the origin, encounters difficulties. Therefore, the displacement of the center of the base at some distance from the ordinate axis (or rather, the time axis) is of practical importance, and in this case it is very important to study the influence of the term $x/{\upsilon }^{2}t$ , which is included in the full formula (1) of the time gradient of the OTV hodograph, on the final results. If the center of the time gradient definition base ${\left(\frac{\Delta t}{\Delta x}\right)}_0$ move a distance0.2 km from the origin, then for the effective velocity at different depths we obtain, respectively: ${\upsilon }_{эф1}$ \u003d 2.238 km / s and ${\upsilon }_{эф1}$ \u003d 2.6 km / s. As can be seen, the displacement of the base center to the side at short times has a significant effect on the velocity value, while at long times it is insignificant. If we reduce the length of the base and bring its center closer to the origin, i.e. let's take $\Delta x$ =0.2 km and Xm = 0.1 km, then for the effective speed we get ${\upsilon }_{эф1}$ \u003d 2.263 km/s and ${\upsilon }_{эф2}$ \u003d 2.608 km/s, respectively. Continuing our research in this direction, we find that $\Delta x$ =0.1 km and Xm = 0.05 km effective speeds acquire the following values: \u003d 2.290 km / s and \u003d 2.690 km / s. An analysis of the data obtained shows that if, at short times, with the approximation of the base of determining the time gradient ${\left(\frac{\Delta t}{\Delta x}\right)}_0$ to the origin of coordinates and decreasing its length, we obtain the desired results, then at large times the errors in determining the effective velocity increase. On the other hand, we know that a decrease in the length of the base leads to an increase in the influence of random factors. Considering all this, in our opinion, if we, in the case of a flank observation system, when determining ${\left(\frac{\Delta t}{\Delta x}\right)}_0$ the center of the base will be shifted to a distance of 0.2 km from the origin of coordinates and its length will be taken equal to $\Delta x$ =0.4 km, then 17 traces will be used to determine the time gradient (with a distance between channels of 0.025 km) and we will obtain a sufficiently high accuracy of calculations. The developed method for determining the effective velocities and refining the velocity model of the medium under study was applied on 3D seismic data in one of the areas of the Azerbaijan sector of the Caspian Sea shelf, which we conventionally called Seda. This area has been repeatedly studied by seismic surveys, but the area under study is complicated by tectonic faults of various ranks and directions, which led to its block structure and to the observed complex wave pattern, so its detailed structure, especially in deep-lying deposits of the Lower Pliocene, Miocene, remains insufficiently studied. Due to the complexity of the structure and the location of deep wells on different blocks (Figure 3).

Figure 3 Time section along one of the 2D Seda seismic profiles a) after the preliminary sum; b) after deconvolution, final stack, filtering and seismic migration.

It became apparent that the existing velocity data do not provide adequate information about the geological structure of the Hasilat III area. Therefore, a velocity model of the medium was compiled using the developed methodology. We analyzed and summarized all the data obtained on given area, calculations were carried out and a three-dimensional velocity model of the medium was compiled (Figure 4).

Figure 4 Calculated velocity models: a) three-dimensional model; b) a three-dimensional model with wells that penetrated seismic horizon VIII, confined to the lower productive strata of the Lower Pliocene.

Then, on the basis of the compiled velocity model, velocity maps were built, one of which is shown in Figure 5, for the target horizons, and based on these data, 2D time sections were transformed into depth sections and seismic migration was applied and more accurate data on the depths of the target horizons were obtained.

Figure 5 Velocity map for SG V productive strata.

1. Analysis of the formula for determining the effective speed shows that of the four parameter $t_{ОГТ}$ , Хm, and $t_{ОГТ}$ ${\left(\frac{\Delta t}{\Delta x}\right)}_{{}_{ОГТ}}$ the definition of the first three does not encounter serious difficulties, and the last one is determined by the method of RNP (controlled directed intake) by L.A. Ryabinkin from seismograms of the series, i.e. field seismograms of single profiling.
2. Errors in the definition do not have a big impact on the final results, because relative errors in velocity values do not exceed 2% $t_{ОГТ}$ .
3. The same can be said about the time gradient determined from the CDP hodograph, i.e. o: errors in the determination of this parameter lead to relative errors in the speed values not exceeding 2% $t_{ОГТ}$ .
4. Gradient of time determined by the hodograph of the OTV ${\left(\frac{\Delta t}{\Delta x}\right)}_0$ greatly affects the speed values, because in this case, the relative errors reach up to 8%; therefore, this parameter must be determined with high accuracy.
5. The proposed method of determination can be easily applied in practice, technologically advanced, because in modern systems of digital processing of seismic data have the software necessary to determine all the parameters included in the formula (5). Therefore, this method of determining the speed can be easily integrated into any processing graph.

None.

The author declares that there is no conflict of interest.

None.

1. Vasiliev SA, Urupov AK. New possibilities for studying the speed of propagation of seismic waves and the structure of the environment from observations at reciprocal points. Applied Geophysics. 1978;92:3–16.
2. Glogovsky VM, Gogonenkov GN. Convergence of an iterative method for determining reservoir velocities from seismic data. Applied Geophysics. 1978;92:65­­­­­­­­–77.
3. Gogonenkov GN, Zakharov ET, Elmanovich SS. Prediction of a detailed velocity section based on seismic data. Applied Geophysics. 1980;97:58–72.
4. Levin AN. Limiting effective speed at CDP for layered-homogeneous media. Applied Geophysics. 1977;86:3–11.
5. Malovichko AA. Determination of the limiting effective speed and degree of inhomogeneity from a single travel time curve of reflected waves in the case of a vertically inhomogeneous medium. Applied Geophysics. 1979;95:35–44.
6. Nevinny AV, Urupov AK. Determination of velocities in environments with curved boundaries (three-dimensional problem). Applied Geophysics. 1977;88:3–18.
7. Puzyrev NN. Time fields of reflected waves and the method of effective parameters. Novosibirsk Science. 1979.
8. Urupov AK, Levin AN. Determination and interpretation of velocities in the method of reflected waves. 1985;67–195.
9. Chernyak VS. Calculation of effective velocities in MOV and CDP for layered media with curvilinear boundaries. Applied Geophysics. 1973;71:71–79.
10. Bear LK, TA Dickens, JR Krebs, et al. Integrated velocity model estimation for improved positioning with anisotropic PSDM: The Leading Edge. 2005;24:622–626.
11. Etienne Robein. Velocities. Time-imaging and Depth-imaging in Reflection Seismics. Principles and Methods, EAGE0. 2003.
12. Jones Ian F. An Introduction to: Velocity Model Building. 2010.
13. Ahmedov TR. Search for optimal velocity characteristics while seismic plotting. Geophysics news in Azerbaijan Baku. 1994;1:18–23.
14. Bancroft JC, Wang S. Converted-wave prestack migration and velocity analysis by equivalent offsets and CCP gathers. CREWES Research Report. 1994;6(28):1–7.
15. Guirigay TA, Bancroft JC. Converted wave processing in the EOM domain. MCREWESResearch Report. 2010;22(23):1–24.
16. Guirigay T. Estimation of Shear wave velocities from PP and PS seismic data using Equivalent Offset Migration: MS thesis, University of Calgary; Alberta, Canada; 2012. 99 p.
17. Wang S. Three-component and three-dimensional seismic imaging: MS thesis, University of Calgary, Alberta, Canada; 1997. 83 p.