eISSN: 2576-4500


Research Article Volume 1 Issue 2
1Department of Engineering, Islamic Azad University, Iran
2Mechanical Engineering Department, Amirkabir University of Technology, Iran
Correspondence: Mohammad Samani, Department of Engineering, College of Mechanical Engineering, Shahre Rey Branch, Islamic Azad University, Tehran, Iran
Received: May 14, 2017 | Published: July 25, 2017
Citation: Samani M, Mahyari MF, Najafinia S. Designing a universal deceleration system for sounding rockets lighter than 100kg by system engineering approach. Aeron Aero Open Access J. 2017;1(2):64-69. DOI: 10.15406/aaoaj.2017.01.00008
For many years deceleration systems are developed in evolutionary fashion. This evolution needed flight test, and experimental data. This research deals with designing a deceleration system for a sounding rocket. It is mainly aimed at designing a universal deceleration system so that the payload touches the land with a safe velocity. To do so, first a deceleration system is designed for a 25kg payload in altitudes of less than 2km. Having considered flight equations for the sounding rocket and parachute, a number of parameters including recovery weight, landing time and velocity and maximum post-deployment acceleration have been computed for sounding rockets lighter than 250kg. Sensitivity analysis of the payload weight and recovery initiation velocity led to designing a universal deceleration system capable of recovering sounding rockets weighing between 25kg and 75kg with a landing velocity between l0m/sec and 12m/sec. Base on system engineering approach, universal deceleration subsystem is design for sounding rocket with various mass.
Keywords: recovery system, sounding rocket, safe landing velocity, system design, parachute deployment initiation velocity, payload, airborne bomblets, rocket power test, ribbon parachute
Sounding rockets are generally designed, manufactured and tested for students to become familiar with rockets, design processes as well as team working. The sounding rockets usually enter the student competitions with a predefined mission. Their history dates back to 19th Century. A vital part of the sounding rockets is a deceleration system for which any failure leads to entire failure of the rocket mission.1 It is very helpful to design quick and easy-to-use universal deceleration system. The universal deceleration system contributes to lower costs, higher reliability and time reduction. Hence it has been utilized in the airborne bomblets whose increased landing velocity shall not be a challenge to mission fulfillment. However, unlike the bomblets, landing velocity and maximum acceleration during the parachute deployment plays an important role in the accomplishment of sounding rockets mission. In other words, increased landing velocity may damage a sounding rocket. In the present research a deceleration system is developed that can be used in sounding rockets with variable weights. To do so, weight variation range and landing velocity of the rocket are needed to be specified.2
In the design and development of today’s aerospace vehicle and bio-capsules equipment, it is frequently essential to conduct tests on particular components under conditions closely simulating those encountered during operations. For all these vehicles, this requires testing at subsonic speeds and at relatively high altitudes. Although tests can be conducted on different test setups and installations such as small scale models in a wind tunnel installation, rocket power test, and water-brake mounted on test vehicle, free flight test vehicle, drop test, rigging test bed, and sled- launched parachute test vehicle; test conditions are still comparatively artificial.3-5
William B et al.5 designed and developed a 24-Ft diameter hybrid Kevlar 29/nylon ribbon parachute in 1980 and tested it with sled test vehicle. Robert E Meyerson6 developed a drag parachute for space shuttle orbiter and tested it in a wind tunnel, the flight test of which was carried out in 2001. Ken Heinde et al.7 developed parachute tests for a missile descent system in 1999, G Guidotti et al.8 designed, developed, tested, and carried out in-flight qualification of a Parachute Recovery System in 2012 . John C Gallon et al.9 did verification and validation testing of the parachute decelerator system prior to the first supersonic flight dynamics test for the low density supersonic decelerator program in 2015.
Sivan J Kenig et al.4 developed rigging test bed for validation of multi-stage decelerator extractions in 2013. Xianyoy Lin10 designed and developed rocket-boosted test for testing a ribbon parachute in 1989. Ricardo A et al. 11 advanced and tested the parachute system for the space station crew return vehicle in 2011. Robert D Braun et al.12 successfully landed five robotic systems on the surface of Mars by supersonic parachute. Development of an Interim Parachute Recovery System for a Re-entry Vehicle was done by William B Pepper Jr13 in 1980. Schatzle PR et al.14 developed a vehicle with a two-stage parachute system in 1980. Design, fabrication, packing and testing of a cross multistage parachute for ARIM-1 Sounding was done by Randy L Thomas15 in 1999. Randy L Thomas16 designed and developed the flight testing of a parachute orientation system to air-launch rockets into low earth orbit in 2007. Fight test has some advantages and disadvantages. Advantages are testing under real conditions with integrated subsystems and obtaining high reliability results.
The flying vehicle is made up of four major subsystems namely propulsion, recovery, and structure and launcher. The propulsion subsystem provides the flying vehicle with required thrust for a certain limited duration, after which the vehicle continues to go up using the kinetic energy until it reaches the state of motionlessness. Having reached the maximum altitude, the system sees an increased velocity in line with increased gravitational acceleration. Then the recovery subsystem comes to play its role in safe recovery of the flying vehicle. Parachute, connection cables, and separation mechanism are the three main parts of this subsystem which is responsible for integrating, stabilizing and reducing the aerodynamic forces exerted on the flying vehicle over the flight course. Figure 1 shows a schematic view of a common recoverable system. Number 1, number 2, number 3 mean propulsion, recovery, structure subsystems.
Design procedure starts with the mission statement which initiates the definition of the sounding rocket system and subsystems’ requirements that lead to vehicle's mission specification. It is followed by mass and energetic determination of the vehicle. Using all this data plus simple mathematical relations, mission implementation starts for the flying vehicle. If the mission implementation meets the requirements, design process finishes; otherwise, mass and energetic determination of the vehicle is modified, until the convergence is met. After the system design of the sounding rocket is completed, a comprehensive recovery system is designed for a range of mass and landing velocity. Figure 2 shows a schematic view of the system design. The mission determination and implementation is necessary for the flying vehicle to embark on a rather vertical trajectory using the propulsion force without any need for flight path control and active stabilizers. Having done the mission, the flying vehicle returns to the earth. Hence, this system is composed of a motor, deceleration subsystem, structure, and a launcher. It is necessary to design and manufacture a light system in order to facilitate the launching operation. Table 1 shows mass distribution for components of such a system.
S. no |
Parameter |
Symbol |
Value |
Units |
1 |
Motor |
|
15 |
Kg |
2 |
Recovery |
|
5 |
Kg |
3 |
Structure |
|
5 |
Kg |
4 |
Overall |
|
span dir="rtl"> 25 |
Kg |
Table 1 Primary design for mass distribution
Having decided on total mass of the flying vehicle and an acceleration of 24m/s2during motor operation phase, the thrust force exerted, can be obtained as follows:
(1)
To maintain reliability, primary force can be taken as 900N .
Considering the primary is to be in equilibrium and motor operating time is a function of flying altitude and vehicle mass. Assuming that drag force is zero and that the vehicle height some 1-.2km upward with inactive motor, , the required system velocity, , at motor burnout can be obtained :
(2)
When this velocity is known, the time needed for reaching the velocity at the constant acceleration of 24m/s2 can be obtained as follows 2
(3)
Supposing that acceleration is constant during the motor burning, altitude achieved h, can be obtained as follows:
(4)
ln this case can be approximated from the following relation :
(5)
This value is within the permissible range. Not only is the drag force overlooked in this approximation , but also the increased acceleration due to constant mass reduction is also ignored. These effects counter act each other.3
Parachutes are generally divided into integrated and strip parachutes. With regard to recovery initiation velocity, the main parachute shall be of integrated type. Since integrated parachutes have a high drag coefficient and their application limits the size of the main parachute, packing space can be minimized. In addition, they show durable stability at low speeds. Integrated parachutes come in various forms including spherical, conical, cruciform and etcetera. Thanks to efficiency of other types of the parachutes semi-spherical and flat annular parachutes are seldom used. For example, not only conical parachutes have higher drag coefficients, they also can tolerate higher tension at the vertex of canopy. These parachutes are mainly used when the forces exerted on the payload from the parachute are insignificant; because of having a shock factor equal to 1.8, they exert a great deal of force onto the payload. It is not possible for the pilot and annular parachutes to have phased-inflation using a reef strap. Compared to other parachutes, extended skirt and cruciform parachutes exert lower primary shock to the payload and are robust enough. So they are compared here to make a choice for the main parachute.4 Extended-skirt parachutes excel the cruciform ones in that they provide a better reefing of the parachute. Cruciform parachutes can only be reefed up to 10% of the main parachute surface area . However, they have lower shock factor, are cheaper and simpler to make, and are small enough not to occupy much space. Nevertheless, it would be better to use cross parachute. Calculations also prove that it is possible to make use of cross parachutes. What is important for the cruciform parachute is the geometrical proportion of the parachute to rope length. The geometrical proportion is expressed as W/l. As this proportion increases, so does the stability. But drag coefficient decreases. Nowadays, proportion is the most frequently used. Hence, this proportion is employed. Figure 3 shows geometrical parameters of the cross parachute.5 According this figure, two parameters are defined for cross parachute which called L and W. Proportion of length of the parachute's ropes to the arm length (structural diameter) shall be minimum 0.7 in cruciform parachutes (l/L). For this research, In order to prevent any drag drop, the aforementioned proportion is assumed to be 0.85.5 In this case drag coefficient will be equal to the average drag coefficient of the cruciform parachutes that is 0.71. To calculate the parachute diameter, Operating conditions are meant for altitude of h=2km above sea level, and air density of . Safe landing velocity is considered below 15m/s. Nominal diameter of the parachute can be obtained from these equations.15
(6)
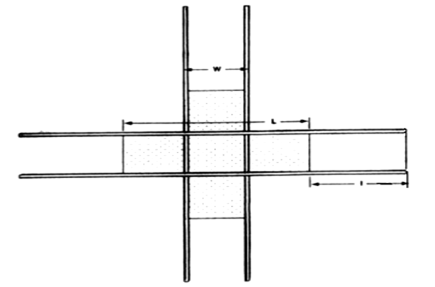
Figure 3 Schematic of parachute layout.5
The proportion of structural diameter to nominal diameter is in cruciform parachutes. Hence, parachute's structural diameter, L, is equal to 4.35m and arm width, W, is equal to 1.45m. According Figure 3 L is equal with 3W, so L is equal 4.35m.5 Based on this calculation, configuration of cross parachute is showed in Figure 4. To calculate maximum permissible velocity of the main parachute deployment the maximum force exerted is taken as:
(7)
Time needed for the parachute (for cruciform parachutes is n=11.7) to be deployed is calculated as follows5
(8)
With regard to the aforementioned calculations, maximum force applied to the parachute is 11g and maximum velocity required for one-phase recovery of the flying vehicle is 31.9m/sec. Time needed to achieve this velocity is 1.36s. In this case, parachute weight is 3.2kg, and cylindrical parachute pack is 10 centimeters thick. It is noteworthy that momentum of the mass ejected from a missile shall be so large that it creates a long distance between the parachute and the rocket, so that the parachute does not come into contact with the rocket. The force required for this operation is provided by a gun that launches the pack. In this case, the launch forces can be calculated as follow :
(9)
Hence a gun or force of 1200N and operation time of 0.01sec is required. Variations of the parachute's drag surface area up to the ultimate inflation time are considered linear with time as follow :
(10)
In order to analyze the tension and to obtain the required robustness for components of the main and drag parachutes, reliability coefficients are mentioned in Table 2.
Parameter |
Safety Factor |
Unit |
Risers |
1/2 |
M |
Suspension line |
91/1 |
M |
Canopy |
85/1 |
M |
Reefing Line |
74/2 |
M |
Drogue Gun Slug |
1/2 |
M |
Table 2 Reliability coefficients for parachute components
Considering the reliability coefficient, the force applied to parachute canvas is 2233.6N/m which is lower than maximum bearable force of the main parachute canvas, 7.6KN/m, stated in MIL-C-7020. So the canvas introduced in MIL-C-7020 is good for the canopy. The number of ropes obtained for the parachute is chosen to be 10; however, because the parachute is cruciform, this value needs to be rounded up to the closest number that is multiple of 4. Hence, the number of ropes is chosen to be 12. Furthermore, each arm of the parachute has 3 ropes that divide the rope into two sections. Considering the reliability coefficient, the parachute riser's resistance is chosen to be 672kgf. It is noteworthy that parachute riser's length is also of significance. Because the riser should be so long that the parachute will not strike the rocket during and after deployment and that it will not be influenced by the rocket trail. Since pilot and main parachutes linger at the end of the rocket during deployment, riser length shall be at least as large as the distance between riser connection point to the end of the rocket (2m) plus at least one winding of the riser around rocket and tails due to roll ( 1.5m). Table 3 shows the main parachute characteristics.
Parameter |
Value |
Nominal Diameter |
3/72 m |
Projected Diameter |
2/6 m |
Structure Diameter |
4/35 m |
Table 3 The main parachute characteristics
In light of the aforementioned calculations, the recovery subsystem consists of a parachute placed into a pack. The parachute connects to the pack through a vent. This connection is referred to as a fuse. Suspension lines are generally sewed to the pack by means of threads which are to be torn apart at a certain time. In order to prevent riser cutoff due to erosion, it is connected to the parachute by means of robust towlines. Tests and flight experience proved that a gun system is good for ejecting the parachute out of the flying vehicle. After the ignition occurs in the gun system cylinder, bullet exits the gun very swiftly. As the bullet leaves the gun, the vent located opposite to the parachute distances itself from the flying vehicle, as a result of which the pack exits its room. In some cases the vent is equipped with a pilot parachute which pulls the main parachute out. Drag parachute is usually of seamed type. The seam enables slow inflation of the parachute which results in reduced shock factor. The pilot parachute of the present research is chosen based on the off-the-shelf parachutes and is aimed at pulling out the main parachute.
Two modes are separately investigated to determine recoverability of the system. Mode one, the system with a weight between 25kg and 250kg is chosen.
First mode
First mode is aimed at determination of the system weight range so that the recovery system is universal. Thrust and propulsion mass are calculated proportionally with permissible acceleration for every flying vehicle followed by simulation. Launch angle is taken as 89 degrees and aerodynamic coefficients have been applied to the simulation program from MD. Table 4 shows that because drag surface area remains constant for all the systems, as the system mass increase so does the landing velocity leading to reduced flight time.7 In addition, the acceleration applied to the system as a result of parachute deployment is less than permissible, which is indicative of suitable parachute design and deployment. Furthermore, near-to-reality conditions are applied to the surface area development during the parachute inflation which leads to lesser shock being applied to the payload during the parachute deployment. Having compared results of the design process with those of the simulation, it can be seen that maximum error of the design process is7%. Table 4 shows these results.
Payload (kg) |
Landing Velocity (m/sec) |
Max Acceleration (m/sec2) |
Landing |
25 |
7.5 |
-26 |
234 |
50 |
10 |
-18 |
174 |
75 |
12.9 |
-15 |
149 |
100 |
15 |
-14 |
134 |
150 |
18 |
-12 |
115 |
250 |
23.5 |
-10 |
96 |
Table 4 Simulation results for various systems' parachute deployment at velocity Vt=3m/sec
Second mode
Second mode, sensitivity analysis of the recovery system is carried out at velocities beyond and below . This mode is aimed at considering the deployment point at two states of lower latitude and higher velocity as well as higher altitude and lower velocity (near acme), which are compared to the specified nominal point. These two states have been simulated for systems of m=75,100, 250kg at three recovery initiation velocities. The results show that increased recovery velocity has not considerable effect on the payload landing velocity. The main reason is that the parachute decelerates the system to the limit velocity, especially at high speed area. In addition, because the parachute has more drag at higher velocities, only negative acceleration applied to the payload during deployment increases. This is evident from the velocity diagram for the systems of m=75,100, 250kg. In Figure 5 weight of payload is 75 kg and parachute simulation done for 3 velocities. It is clear, landing velocities are same but in the higher velocities payload has more negative acceleration. If weight of payload increase to 100 kg and 250 kg, payload has same action but landing velocities are changed to 15 and 23.61 m/sec (Figure 6 & 7). These diagrams are shown in (Figures 5-7) which show that the range between m=100kg and m=250kg has unsafe velocities. As Figure 8 shows, because absolute value of the acceleration at deployment time for systems of m=75, 100, 250kg is less than the acceleration of the lower-mass systems, acceleration curve moves faster to zero, as a result of which velocity of higher-mass systems remains at unsafe area, and there will be no more chance for more velocity increase.
In this study, the preliminary design and detailed design of a sounding rocket via system engineering approach is carried out .Regarding defined Mass distributions, Table l, Mass of recovery subsystem is determined for different mass of payloads. System design is a holistic approach that considers all aspects of sounding rocket in making design choices. Different design choices give rise to bigger problem scope and therefore, solution space. Therefore, with the support of simulation, the recovery subsystem is investigated (Table 4). The flowchart in Figure 2 is the major determinant of solution convergence.
Parameter |
Unit |
Description |
|
---- |
Rolling, Pitching and Yawing moment coefficients |
|
N |
Aerodynamic force of the parachute |
|
Kg/m3 |
Density of air |
M |
---- |
Mach number |
|
Radian |
Roll, Pitch and Yaw Euler angles |
|
Radian/S |
Components of the angular velocity |
|
m/S |
Components of velocities in body coordinates |
|
Kg |
Mass of motor |
|
Kg |
Mass of structure |
|
N |
thrust force |
|
m |
Max altitude |
L |
m |
Canopy panel length |
|
m |
Displacement of spring |
|
---- |
Stiffness of the spring force |
|
m |
Parachute displacement |
|
N |
Spring force vector |
|
m |
Payload displacement vector |
|
---- |
Quaternion |
|
N |
Vector of aerodynamic and propulsion forces |
|
Kg |
Mass of recovery |
|
Kg |
Overall mass |
|
m/S |
Required system velocity |
CD |
---- |
Drag coefficient |
W |
m |
canopy panel width |
Table 5 Nomenclature
Comparing results of the design process with those of the simulation shows that design process results come with a maximum error of 7%. Furthermore, deceleration systems are capable of safe recovery of the sounding rockets weighing between 25kg to 78 kg at landing velocities between10 m/s2 to 12.9m/s2. Weights beyond the above-mentioned values lead to unsafe landing of the rocket and exert damage to the payload. In addition, changing the recovery initiation point of the rockets up to 250kg does not have noticeable effect on the payload landing velocity. The reason is that the limit velocity is quickly reached. The velocity diagrams show that reaching high altitudes during deployment have very little effect on bringing about safe velocity for higher-mass payloads. So, off-limit landing velocity is safe for these systems and the parachute designed for lighter than m=100kg systems is considered a universal parachute. It can be seen that maximum error of the design process is7%. Table 4 shows these results.
None.
Author declares that there is no conflict of interest.

©2017 Samani, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.