Future spacecraft are envisioned as autonomous, miniature, and intelligent space systems. This paper describes the design and implementation of a model predictive control (MPC) system for satellite attitude control. The MPC algorithm is designed to successfully deal with constraints due to the small control torque given by magnetic torques and the Earth’s magnetic field. Laguerre functions are proposed to simplify the implementation of the MPC controller for on-line computation. A control system processor is designed as a peripheral hard core of the system-on-chip for satellite on-board data handling. Targeting the FPGA technology, this processor runs up to 120 MHz.

Keywords: satellite dynamics, nanosatellites, matlab simulations, magnetorquers, vernal equinox direction, orthogonal triad, quaternion method, attitude transformation matrix, euler angle, laguerre functions, hildreth’s quadratic programming, xilinx virtex-4, fpga technology, accumulator

MPC, model predictive control; FPGA, field programmable gate array; MPQPs, multi parametric quadratic programs; CSP, control system processor; MAC, multiply and accumulation; SoC, system-on-chip; OBDH, on board data handling system; MPCSP, model predictive control processor; ECI, earth centred inertial; MIMO, multiple input, multiple output; AMBA, advanced microcontroller bus architecture

Conventional satellite systems are designed and purpose built over many years with significant expense and undertaking, with the result that the technology is obsolete by the time of launch. However, a new approach to satellite development which builds upon the rapid changes in computer hardware technology is quickly taking place around the world within university and government research labs. The development of what is known as nano satellites, with typical mass less than 10kg, is quickly transforming the Space development scene as it allows engineering and science researchers to send into orbit various payloads within a short time at low cost. In particular, in the last 10 years many universities like Stanford¹ have carried out university satellite programs, and nano satellites have been built and successfully launched into space. Such small satellite can be controlled by various actuation methods, including thrusters, reaction wheels, magnetic torquers, or a combination of above. Currently electromagnetic actuator is the most effective approach, and has been adopted for many nano satellite missions, e.g. the CanX-1,² AAUSat,³ Compass One⁴ and so on.

The magnetic torquer interacts with the earth’s own magnetic field in order to generate a control torque acting on spacecraft. An advantage of magnetic torquers is that they require no fuel and so have virtually unlimited life. They do of course require electrical power, but there is no exhaust pollutant and by providing a couple they are not sensitive to movement of the centre of mass. One drawback of this control technique is that the torques which can be applied to the spacecraft for attitude control purposes are constrained to lie in the plane orthogonal to earth magnetic field, and hence the satellite is under-actuated. In the equatorial plane, the magnetic field line always lie horizontally, north-south. Consequently a spacecraft whose orbit lies in this plane cannot use magnetic torquers to counteract the north-south component of their disturbance torque, or to dump this component of momentum. For an inclined orbit, suitable variation of the magnetic field allows controllability in the long term, but presents a significant challenge from a control perspective.⁵

A novel approach to the magnetic attitude control problem, based on Model predictive control has been demonstrated as a suitable candidate in many literatures⁶ presents a thorough review of the area of magnetic control, and develops a closed form solution for MPC based controller under the constraints of earth’s magnetic field. The author also points out that the optimal solution cannot be given in closed form if the constraints on the coils’ magnetic dipoles become active. The systemic method to deal with these equality and inequality constraints in MPC is to operate online quadratic programming.⁷ However, it has recently been shown that a great deal of the computational effort in traditional MPC can be done offline. Algorithms have been presented for solving multi-parametric quadratic programs (MPQPS) that are used to obtain explicit solutions to the MPC problem. Thus, the explicit model predictive controller accomplishes online MPC functionality without solving an optimization problem at each time step.⁸ Ref.⁹ investigates MPC for attitude control using magnetic torque rod. The design is carried out based on the closed form solution for MPC based attitude controller when considering the Earth’s magnetic field. Ref.⁹ further develops a MPC based magnetic controller to deal with the problem of Low Earth orbiting satellites attitude control under significant disturbances from the external environment including aerodynamic forces, gravity gradient torques and residual magnetic dipoles. However, except the constraint in the Earth’s magnetic field, for Nano satellites the magnetic coil provides very small torque (in the order of 10-9 N-m). Hence, both the actuator saturation and the Earth’s magnetic field constraints should be considered in MPC algorithm design.

The MPC algorithm results in very complex matrix operations, which limit its feasibility for small satellites. In real-time control, to execute extremely fast control laws for feedback systems, a control system processor (CSP) was designed.^10,11 The excellent performance of the CSP is achieved by implementing simple mixed data formation, with 24-bit fixed point data for state variables and 11-bit low precision floating data for coefficients. The CSP takes advantage of single processing element, i.e. multiply and accumulation (MAC) to execute all the arithmetic operation. In,¹² another dedicated control system processor was developed based on 1-bit processing.¹³ In this processor architecture, no multiply operation is required, which greatly increased the hardware performance in terms of power, area and speed. In this paper, to effectively implement the MPC, the controller structure is simplified using Laguerre functions.¹⁴ At the same time, a system-on-chip (SoC) is proposed for the satellite on-board data handling system (OBDH). This paper presents an innovative model predictive control system processor (MPCSP) as a peripheral hardcore of the SoC for satellite attitude control. The MPCSP is a very efficient design in terms of power, area and speed for real-time control.

The remaining paper is organised as follows. In section 2 three basic reference frames used in satellite attitude control are introduced first, followed by a description of satellite attitude dynamics. Secondly, a linearised dynamic model is presented in Euler angle method. At the end of this section, Earth’s magnetic field model is demonstrated and some constraints on control torque are discussed. Section 3proposes a novel MPC approach using Discrete-time Laguerre networks in magnetic attitude control problem. Section 4 introduces the MPCSP design. Section 5 presents the simulation results for attitude control of a student-built Nano satellite. Section 6 concludes.

Reference frames

Earth Centred Inertial (ECI) reference frame: The origin of these axes is in the Earth’s centre. The X axis is parallel to the line of nodes, which is the intersection between the Earth’s equatorial plane and the plane of the ecliptic, and is positive in the Vernal equinox direction (Aries point). The Z axis is defined as being parallel to the Earth’s Geographic north-south axis and pointing north. The Y axis completes the right-handed orthogonal triad.

Orbit reference frame: The origin of this orbit reference frame moves with the cm (centre of mass) of the satellite in the orbit. The Z axis points toward the cm of the earth. The X axis is in the plane of the orbit, perpendicular to the Z axis, in the direction of the velocity of the satellite. The Y axis is normal to the local plane of the orbit, and completes a three-axis right-hand orthogonal system. Satellite body reference frame: The origin of this reference frame is in the satellite centre of mass; the axes are assumed to coincide with the body’s principal inertial axes.

Spacecraft nonlinear attitude model

The attitude dynamic equations are obtained from Euler’s moment equation as follows.¹⁵

$h=-{\omega }_{\text{sb}/\text{ECI}}^B\times h+T$ (1)

Where $h=-{\omega }_{\text{sb}/\text{ECI}}^B\times h+T\in R^3$ , is angular velocity vector of satellite body reference frame with respect to inertial reference frame, expressed in satellite body reference frame, h is angular momentum vector of the entire system, expressed in satellite body system. h denotes differentiation of h in the body frame and T is the sum of external torques.

For a rigid satellite, $h=I\omega ,$ where I is the satellite inertia matrix expressed in the body frame, so the attitude dynamic equations reduce to well-known form

$$I{\text{<mover accent="true"> ω <mo>˙</mo> </mover>}}_{\text{sb}/\text{ECI}}^B={-}_{\text{sb}/\text{ECI}}^B\times I_{\text{sb}/\text{ECI}}^B+T$$ (2)

${\text{ω}}_{\text{orb}/\text{ECI}}^{\text{B}}=A(q)\left[\begin{array}{c}0\\ -{\text{ω}}_0\\ 0\end{array}\right]$ (3)

where ${\text{ω}}_0$ is the orbital angular rate, A(q) is the attitude matrix with respect to the orbital reference frame and ${\text{ω}}_{\text{orb}/\text{ECI}}^{\text{B}}\in R^3$ is angular velocity vector of orbit reference frame with respect to inertial reference frame, expressed in satellite body reference frame. For earth pointing satellite, we always consider the orbit reference frame as an attitude reference, so that

${\text{ω}}_{\text{sb}/\text{orb}}^{\text{B}}={\text{ω}}_{\text{sb}/\text{ECI}}^{\text{B}}-\text{A}\left(\text{q}\right)\left[\begin{array}{c}0\\ -{\text{ω}}_0\\ 0\end{array}\right]$ (4)

Where ${\text{ω}}_{\text{sb}/\text{orb}}^{\text{B}}\in {\text{R}}^3$ , is angular velocity vector of satellite body reference frame with respect to orbit reference frame, expressed in satellite body reference frame. When the satellite has the desired attitude, the satellite body reference frame must remain aligned with orbit reference frame.

Linearised attitude dynamics model

The Laguerre MPC control algorithm requires a linearized dynamic model. It should be pointed out that in the derivation of the linearized attitude dynamics model, we assume a circular orbit for the satellite we also assume the inertia matrix is diagonal.

Besides quaternion method, attitude transformation matrix can be expressed with Euler angle $(\varphi ,\theta ,\psi )$ . The roll angle $(\varphi )$ is defined as a rotation about the x body axis, the pitch angle (θ) about the y body axis, and the yaw angle $(\psi )$ about the z body axis. Assuming small variation of the Euler angles, the attitude transformation matrix becomes:

$\left[{{\rm A}}_{\alpha \beta \lambda }\right]\approx \left[\begin{array}{ccc}1& \psi & -\theta \\ \psi & 1& \varphi \\ \theta & -\varphi & 1\end{array}\right]$ (6)

And one also obtains that:

$\dot{\varphi }\approx {\text{ω}}_{\text{sb}/\text{orbx}}^{\text{B}},\text{<mover accent="true"> θ <mo>˙</mo> </mover>}\approx {\text{ω}}_{\text{sb}/\text{orby}}^{\text{B}},\text{<mover accent="true"> ψ <mo>˙</mo> </mover>}\approx {\text{ω}}_{\text{sb}/\text{orbz}}^{\text{B}}$

So Eq. 4 becomes

${\omega }_{sb/ECI}^{{\rm B}}={\omega }_{sb/orb}^{{\rm B}}+\left[{{\rm A}}_{\alpha \beta \gamma }\right]\left[\begin{array}{c}0\\ -{\omega }_0\\ 0\end{array}\right]$ (7)

With these assumptions in (6), (7) becomes

${\text{<mover accent="true"> ω <mo>˙</mo> </mover>}}_{\text{sb}/\text{ECIx}}^{\text{B}}=\ddot{\varphi }-{\text{<mover accent="true"> ψ <mo>˙</mo> </mover> ω}}_0$

${\text{<mover accent="true"> ω <mo>˙</mo> </mover>}}_{\text{sb}/\text{ECIy}}^{\text{B}}=\text{<mover accent="true"> θ <mo>¨</mo> </mover>}$

${\text{<mover accent="true"> ω <mo>˙</mo> </mover>}}_{\text{sb}/\text{ECIz}}^{\text{B}}=\text{<mover accent="true"> ψ <mo>¨</mo> </mover>}+\dot{\varphi }{\text{ω}}_0$

Finally, the satellite attitude dynamics are approximated well by a linear model.¹⁶

$\text{<mover accent="true"> x <mo>˙</mo> </mover>}=\text{Ax}+\left[\begin{array}{c}{0}_{3,3}\\ {\text{I}}^{-1}\end{array}\right]\left({\text{T}}_{\text{d}}+{\text{T}}_{\text{c}}\right)$ (9)

Where,

${\rm A}=\left(\begin{array}{cccccc}0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ -4{\omega }_0^2{\sigma }_1& 0& 0& 0& 0& {\omega }_0\left(1-{\sigma }_1\right)\\ 0& 3{\omega }_0^2{\sigma }_2& 0& 0& 0& 0\\ 0& 0& {\omega }_0^2{\sigma }_3& -{\omega }_0\left(1+{\sigma }_3\right)& 0& 0\end{array}\right)$

$X={\left[\varphi \theta \psi {\omega }_{sb/orbx}^{{\rm B}}{\omega }_{sb/orby}^{{\rm B}}{\omega }_{sb/orbxz}^{{\rm B}}\right]}^{{\rm T}}$

Where T_d is disturbance torque which is considered as zero in this paper, ${\text{T}}_{\text{c}}$ is control torque and

${\text{σ}}_1=\frac{\left({\text{I}}_{\text{y}}-{\text{I}}_{\text{z}}\right)}{{\text{I}}_{\text{x}}},{\text{σ}}_2=\frac{\left({\text{I}}_{\text{z}}-{\text{I}}_{\text{x}}\right)}{{\text{I}}_{\text{y}}},{\text{σ}}_1=\frac{\left({\text{I}}_{\text{x}}-{\text{I}}_{\text{y}}\right)}{{\text{I}}_{\text{z}}}$ .

Magnetic attitude control

The controlling torque acting on spacecraft is produced by the interaction between a magnetic moment generated within a spacecraft and the earth’s magnetic field:

${\text{T}}_{\text{C}}=\text{m}\times b$ (10)

Where m is the generated magnetic moment inside the body and b is the earth’s magnetic field intensity.
Eq. 10 can be rewritten as,

$\left[\begin{array}{c}{\text{T}}_{\text{Cx}}\\ {\text{T}}_{\text{Cy}}\\ {\text{T}}_{\text{Cz}}\end{array}\right]=\left[\begin{array}{ccc}0& -{\text{b}}_{\text{z}}& -{\text{b}}_{\text{y}}\\ -{\text{b}}_{\text{z}}& 0& -{\text{b}}_{\text{x}}\\ {\text{b}}_{\text{y}}& -{\text{b}}_{\text{x}}& 0\end{array}\right]\left[\begin{array}{c}{\text{M}}_{\text{x}}\\ {\text{M}}_{\text{y}}\\ {\text{M}}_{\text{z}}\end{array}\right]$ (11)

A dipole approximation of the Earth’s magnetic field is given in the following equation expressed in orbit reference frame.⁹

$\left[\begin{array}{c}{b}_x^{orb}\\ b_y^{orb}\\ b_z^{orb}\end{array}\right]=\frac{{\mu }_f}{a^3}\left[\begin{array}{c}\cos {\omega }_{0}t\sin (i_m)\\ -\cos (i_m)\\ 2\sin ({\omega }_0)t\sin (i_m)\end{array}\right]$ (12)

Where i_m is the inclination of the satellite’s orbit with respect to the magnetic equator, and a is the orbit’s semi-major axis. Time is measured from t=0 at the ascending-node crossing of the magnetic equator. The field’s dipole strength is ${\text{μ}}_{\text{f}}=7.9\times {10}^{15}Wb-m.$

The magnetic field in satellite body reference frame is given by

$\text{b}=\text{A}\left(\text{q}\right){\text{b}}^{\text{orb}}$ (13)

Constraints in magnetic attitude control

In Eq. 10, m must satisfy orthogonality conditions with respect to T_C and b, so one must have,

${\text{T}}_{\text{C}}{}^{\text{'}}\text{b}=0$ (14)

Beside, constraints on the coils’ magnetic dipoles (actuators’ saturation) play an important role in the formulation of the magnetic attitude control problem. Such constraints are of the form

${\text{m}}_{\min }\le \text{m}\le {\text{m}}_{\max }$ (15)

The magnetic dipole m is given by.⁶

$\text{m}=\frac{1}{{\left|\text{b}\right|}^2}\text{B}{\left(\text{b}\right)}^{\text{'}}{\text{T}}_{\text{C}}$ (16)

Where,

$\text{B}\left(\text{b}\right)=\left[\begin{array}{ccc}0& {\text{b}}_{\text{z}}& -{\text{b}}_{\text{y}}\\ -{\text{b}}_{\text{z}}& 0& {\text{b}}_{\text{x}}\\ {\text{b}}_{\text{y}}& -{\text{b}}_{\text{x}}& 0\end{array}\right]$ (17)

So the constraints on coils’ magnetic dipoles can be translated into constraints on the control variable TC Using Eq. 17, it follows that

${\text{m}}_{\min }\le \frac{1}{{\left|\text{b}\right|}^2}\text{B}{\left(\text{b}\right)}^{\text{'}}{\text{T}}_{\text{C}}\le {\text{m}}_{\max }$ (18)

which in turn implies

$\left[\begin{array}{c}-\text{B}\left(\text{b}\right)\\ \text{B}\left(\text{b}\right)\end{array}\right]{\text{T}}_{\text{C}}\le \left[\begin{array}{c}{\text{m}}_{\max }\\ {\text{m}}_{\min }\end{array}\right]{\left|\text{b}\right|}^2$ (19)

Here the mathematic expressions and derivations of MPC algorithm are given. It should be pointed out that the idea of Laguerre MPC is proposed by Wang. In this thesis, however, we will be concerning on the Laguerre MPC.

The plant to be controlled is described by the discrete time model of the form as

$x_m\left(k+1\right)=A_m{x}_m\left(k\right)+B_{m}u\left(k\right)$

$y\left(k+1\right)=C_m{x}_m\left(k\right)$ (2.20)

Assume that the plant has p inputs, q outputs and n states. Let us denote the difference of the state variable by

$\Delta x_m\left(k+1\right)=x_m\left(k+1\right)-x_m\left(k\right)$ (2.21)

And the difference of the control variable by

$\Delta u\left(k\right)=u\left(k\right)-u\left(k-1\right)$ (2.22)

Then we augment the original state space model (2.21) and (2.22) as

$\stackrel{x\left(k+1\right)}{\stackrel{\uparrow }{\left[\begin{array}{c}\Delta x_m\left(k+1\right)\\ y\left(k+1\right)\end{array}\right]}}=\stackrel{A}{\stackrel{\uparrow }{\left[\begin{array}{cc}{A}_m& o_m^T\\ C_m{A}_m& I_{q\times q}\end{array}\right]}}\stackrel{x\left(k\right)}{\stackrel{\uparrow }{\left[\begin{array}{c}\Delta x_m\left(k\right)\\ y\left(k\right)\end{array}\right]}}+\stackrel{B}{\stackrel{\uparrow }{\left[\begin{array}{c}{B}_m\\ C_m{B}_m\end{array}\right]}}\Delta u\left(k\right)$

$y\left(k\right)=\stackrel{C}{\stackrel{\uparrow }{\left[\begin{array}{cc}{o}_m& I_{q\times q}\end{array}\right]}}\left[\begin{array}{c}\Delta x_m\left(k\right)\\ y\left(k\right)\end{array}\right]$ (2.23)

Now we model the control signal by forward operators. Let us denote the vector

$Y={\left[y\left(k_i+1\text{|}{k}_i\right)y\left(k_i+2\text{|}{k}_i\right)y\left(k_i+3\text{|}{k}_i\right)\cdots y\left(k_i+N_p\text{|}{k}_i\right)\right]}^T$

$\Delta U={\left[\Delta u\left(k_i\right)\Delta u\left(k_i+1\right)\Delta u\left(k_i+2\right)\cdots \Delta u\left(k_i+N_c-1\right)\right]}^T$

The cost function of Traditional MPC is expressed as

$J={(R_s-Fx(k_i))}^T(R_s-Fx(k_i))-2\Delta U^T{\varphi }^T(R_s-Fx(k_i))+\Delta U^T({\varphi }^T\varphi +\overline{R})\Delta U$ (2.24)

Where,

$F=\left[\begin{array}{l}\begin{array}{c}CA\\ C{A}^2\\ C{A}^3\\ ⋮\end{array}\\ C{A}^{N_P}\end{array}\right],\varphi =\left[\begin{array}{ccccc}CB& 0& 0& \cdots & 0\\ CAb& CB& 0& \cdots & 0\\ C{A}^{2}B& CAB& CB& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ C{A}^{N_p-1}B& C{A}^{N_p-2}B& C{A}^{N_p-3}B& \cdots & C{A}^{N_p-N_c}B\end{array}\right]$

$I_{q\times q}$ is a $q\times q$ identity matrix, R_S is the set point vector, $\overline{R}$ is the weighting matrix for control signal, N_C is control horizon, N_pis prediction horizon. The triplet (A, B, C) is called the augmented model.

Now we calculate derivation of the cost function J:

$\frac{dJ}{d\Delta U}=-2{\Phi }^T\left(R_s-Fx\left(k_i\right)\right)+2\left({\Phi }^T\Phi +\overline{R}\right)\Delta U$ (2.2.5)

The necessary condition of the minimum J is obtained

$\frac{dJ}{d\Delta U}=0$                (2.2.6)

The optimal solution for the control signal is

$\Delta U={\left({\Phi }^T\Phi +\overline{R}\right)}^{-1}{\Phi }^T\left(R_s-Fx\left(k_i\right)\right)$ (2.2.7)
Now we derive the close-form control law. Because of the receding horizon control principle, we only take the first element of $\Delta U$ at time k_i as the incremental control, thus
$\Delta u\left(k_i\right)=\left[10\dots 0\right]{\left({\Phi }^T\Phi +\overline{R}\right)}^{-1}{\Phi }^T\left(R_s-Fx\left(k_i\right)\right)=K_{y}r\left(k_i\right)-K_{mpc}x\left(k_i\right))$ (2.28)

Where $K_y$ is the first element of ${\left({\Phi }^T\Phi +\overline{R}\right)}^{-1}{\Phi }^T{R}_S$ and $K_{mpc}$ is the first row of ${\left({\Phi }^T\Phi +\overline{R}\right)}^{-1}{\Phi }^{T}F$ . (2.28) is in a standard form of linear time-invariant state feedback control. The state feedback control gain vector is K_mpc. Therefore, with the augmented design model

$x\left(k+1\right)=Ax\left(k\right)+B\Delta u\left(\text{k}\right)$

The closed-loop system is obtained by substituting (2.28) into the augmented system equation; changing index k_i to k, leading to the closed-loop equation

$x\left(k+1\right)=\left(A-B{k}_{mpc}\text{x}\left(\text{k}\right)\right)+\text{B}{k}_y\text{r}\left(\text{k}\right)$ (2.29)

Thus we can see when constraints have not been taken in to consideration, the MPC control algorithm can be written as a closed-loop form. All parameters required in MPC control algorithm can be calculated off-line and the on-line computational demand is relatively low.

Laguerre MPC

Now we model the control signal with Laguerre functions. Laguerre functions are a set of discrete orthonormal basis functions that can be expressed as

${\Gamma }_k\left(z\right)={\Gamma }_{k-1}\left(z\right)\left(\frac{z^{-1}-a}{1-a{z}^{-1}}\right)$ (2.30)

${\Gamma }_1\left(z\right)=\frac{\sqrt{1-a^2}}{1-a{z}^{-1}}$ (2.31)

Letting $l_i\left(k\right)$ denote the inverse z-transform of ${\Gamma }_i\left(z,a\right),$

$L\left(k\right)={\left[\begin{array}{ccc}{l}_1\left(k\right)& l_2\left(k\right)& \begin{array}{cc}\cdots & l_N\left(k\right)\end{array}\end{array}\right]}^T$

The set of discrete-time Laguerre functions satisfies the following difference equation:

$\text{L}\left(\text{k}+1\right)={\text{A}}_{\text{l}}\text{L}\left(\text{k}\right)$ (2.32)

where the initial condition is given by

$L{\left(0\right)}^{{\rm T}}=\sqrt{\beta }\left[1-a{a}^2-a^3\dots {\left(-1\right)}^{{\rm N}-1}{a}^{{\rm N}-1}\right]$ (2.33)
a is the Laguerre scaling factor, $\text{β}=\left(1-{\text{a}}^2\right)$ , and A₁ is a N×N matrix. For example N=5,

${{\rm A}}_{\lambda }=\left[\begin{array}{ccccc}\alpha & 0& 0& 0& 0\\ \beta & \alpha & 0& 0& 0\\ -\alpha \beta & \beta & \alpha & 0& 0\\ {\alpha }^2\beta & -\alpha \beta & \beta & \alpha & 0\\ -{\alpha }^3\beta & {\alpha }^2\beta & -\alpha \beta & \beta & \alpha \end{array}\right]$

$L{\left(0\right)}^{{\rm T}}=\sqrt{\beta }\left[1-\alpha {\alpha }^2-{\alpha }^3\dots {\left(-1\right)}^{{\rm N}-1}{\alpha }^{{\rm N}-1}\right]$ .

The Laguerre functions can be used to describe the impulse response of the stable system. If we consider the future control signals in model predictive control as the impulse response of a SISO system, $\Delta u$ can be described as

$\Delta u\left(k_m+k\right)=\text{L}{\left(\text{k}\right)}^{\text{T}}\eta$ (2.34)
where $\eta ={[c_1{c}_2\cdots c_N]}^T.$

For a MIMO system, $\Delta u\left(k_m+k\right)$ is given in following equation:

$\text{Δu}\left({\text{k}}_{\text{m}}+\text{k}\right)=\left[\begin{array}{ccc}\begin{array}{cc}{\text{L}}_1{\left(\text{k}\right)}^{\text{T}}& 0\\ 0& {\text{L}}_2{\left(\text{k}\right)}^{\text{T}}\end{array}& \begin{array}{c}\cdots \\ \cdots \end{array}& \begin{array}{c}0\\ 0\end{array}\\ \begin{array}{cc}\cdots & \cdots \end{array}& \ddots & ⋮\\ \begin{array}{cc}0& 0\end{array}& \cdots & {\text{L}}_{\text{p}}{\left(\text{k}\right)}^{\text{T}}\end{array}\right]\text{η}$ (2.35)

Where ${\text{Δu(k}}_m\text{)}$ is the current incremental control, $\text{Δu}\left({\text{k}}_{\text{m}}+\text{k}\right)$ is the future incremental control at sample k and ${\text{L}}_1\left(\text{k}\right)$ represents the Laguerre network description for the i^th control. The input matrix can be partitioned to

$B=[B_1{B}_2\cdots B_p].$

Then the cost function becomes

$\text{J}={\text{η}}^{\text{T}}\text{Ωη}+2{\text{η}}^{\text{T}}\text{ψx}\left({\text{k}}_{\text{i}}\right)$ (2.36)

Where the matrix $\text{Ω}$ and $\psi$ are

$\text{Ω}={\displaystyle {\sum }_{m=1}^{N_p}\varphi \left(\text{m}\right)\text{Q}\varphi {\left(\text{m}\right)}^{\text{T}}+{\text{R}}_{\text{L}}}$

$\psi ={\displaystyle {\sum }_{m=1}^{N_p}\varphi \left(\text{m}\right){\text{QA}}^{\text{m}}}$

$\varphi {(m)}^T={\displaystyle {\sum }_{(j=0)}^{(m-1)}{A}^{(m-j-1)}[B_1{L}_1{(j)}^T{B}_2{L}_2{(j)}^T\cdots B_p{L}_p{(j)}^T}]$

B_iis the i^th column of the B matrix, Q and R_L are weighting matrix, $Q=C^T\times C$ is weighting matrix for state variables, ${\text{R}}_{\text{L}}={\text{r}}_{\text{w}}\times {\text{I}}_{\text{N}\times \text{N}}$ is a diagonal matrix (N × N) for control variables $\eta$ .

The object of model predictive control is to solve an optimization problem that takes into account the constraints. Although model predictive control is able to deal with many kinds of constraints either on control signals or on output signals, here we will only focus on constraints on the Amplitude of the Control Variables. Optimization in MPC is realized by minimizing the object function subject to some constraints, which can be considered as a quadratic programming problem. The objective function J and the constraints in Quadratic Programming are expressed as

$\text{J}=\frac{1}{2}{\text{x}}^{\text{T}}\text{Ex}+2{\text{x}}^{\text{T}}\text{F}$ (2.37)

${\rm M}x\le \gamma$ (2.38)

Where E, F, M and $\text{γ}$ are compatible matrices and vectors in the quadratic programming problem.
A simple algorithm called Hildreth’s Quadratic Programming was proposed to solve Quadratic Programming problem. The iteration expression of Hildreth’s Quadratic Programming Procedure is given in following equation:

${\lambda }_i^{m+1}=\max \left(0,{\omega }_i^{m+1}\right)$ (2.39)

Where ${\omega }_i^{m+1}=-\frac{1}{h_{ii}}\left[k_i+{\displaystyle {\sum }_{\text{j}=1}^{\text{i}-1}{h}_{ij}{\lambda }_j^{m+1}}+{\displaystyle {\sum }_{\text{j}=\text{i}+1}^n{h}_{ij}{\lambda }_j^m}\right]$ (2.40)

m means the m^th iteration, the scalar $h_{ii}$ is the ij^th element in the matrix $H=M{E}^{-1}{M}^T$ and k_i is the i^th element in the vector. $K=\text{γ}+{\text{ME}}^{-1}\text{F, }\lambda$ is a column vector called Lagrange multiplier. The number of its components is equal to the number of inequality equations for input constraints and ${\lambda }_i$ is the i^th component of the Lagrange multiplier.

When the iteration is completed, the converged Lagrange multiplier ${\lambda }^{\text{*}}$ contains either zero or positive values. The constrained minimization over x is given by

$x=-{\text{E}}^{-1}\left(\text{F}+{\text{M}}^{\text{T}}{\text{λ}}^{\text{*}}\right)$ (2.41)

As it can be seen from (2.40), the on-line computation demand of MPC is mainly determined by the size of matrix $H=M{E}^{-1}{M}^T$ . The size of matrix M is determined by the number of inequality equations, which can’t be changed; therefore the size of matrix E is the critical factor for decreasing the on-line computation requirement.

For traditional MPC, the cost function is given in (2.24). To perform optimization, we substitute the matrix E in (2.37) with matrix $\left({\Phi }^T\Phi +\overline{R}\right)$ . It should be noted that the size of matrix $\left({\Phi }^T\Phi +\overline{R}\right)$ is ${\text{(N}}_{\text{c}}\times \text{p})\times ({\text{N}}_{\text{c}}\times \text{p})$ and hence it can be concluded that the number factors involved in on-line computation is determined by the control horizon ${\text{N}}_{\text{c}}$ . For some complex dynamic system, ${\text{N}}_{\text{c}}$ has to be selected greater than 80 to stabilize the system, which will lead to a large computation demand.

For Laguerre MPC, the matrix E in (2.37) can be substituted by $\text{Ω}$ , which is a ${\text{(N}}_{\text{c}}\times \text{p})\times ({\text{N}}_{\text{c}}\times \text{p})$ matrix. The number of factors involved in on-line computation is decided by the Parameter N. It should be noted that N can be a factor of ${\text{N}}_{\text{c}}$ when the Laguerre scaling factor a is selected greater than zero, which means the factors involved in on-line computation will be decreased greatly when Laguerre functions are utilized in MPC design. If a is equal to zero, N has to be chosen to be equal to ${\text{N}}_{\text{c}}$ and under this situation the Laguerre MPC becomes identical to traditional MPC. This is a very attractive property of Laguerre MPC because we can easily compare the performances of these two MPC algorithms by change the value of Laguerre scaling factor a

Different types of control applications require different implementation solutions. Most MPC applications target process control, in which sample periods are low and the plant is physically large, meaning that processing based upon an industrial computer is adoptable. However, the proposed electro-magnetic control system is targeting very small satellites, in which the controller hardware must be embedded. It may require very high sampling rate for precise attitude control. Also executing the MPC is relatively complex with heavy matrix operations. It is therefore requires some high performance device for control system processing.

SoC for satellite on-board data handling

There are two types of satellite on-board data handling systems: central and distributed. The central processing approach has one on-board computer to deal with all the data processing for each subsystem. The distributed processing approach, however, has many on-board computers. Some subsystems may have more than one processor. Nowadays most of the satellites adopt the distributed approach, but for nanosatellites this approach is not efficient due to the limited size and power. Hence, the SoC solution is proposed not only for attitude control but also for data processing for other subsystems.

The SoC can implement the whole digital functionality of the satellite on a single chip. The gate densities achieved in current FPGA devices have enough logic gates/elements to implement different functionalities on the same chip by mixing self-designed modules with third party ones. In the SoC, it contains dedicated processors for each subsystem. Figure 1 shows the SoC architecture. It contains a general purpose processor and the dedicated processors. Its structure comprises an AMBA¹⁷ compliant bus that communicates between the general purpose processor and the control system processor. Generally, the MPCSP is independent, but the general purpose processor as the controller of the SoC monitors the control state variables and satellite attitude information from the inertial sensors. These data are a part of telemetry information for satellite housekeeping.

Figure 1 Soc architecture for satellite OBDH.

MPCSP design and implementation

To map the control algorithm to processor architecture, it is divided into tasks or processes. These processes include data input and output (IO), data storage (Memories), timer, instruction fetching and decoding, next instruction address calculation (Program Counter) and arithmetic operations (ALU). This partitioning should allow all the processes to be mapped easily into hardware, minimizing the resources required.

The number of concurrent operations can determine the amount and functionality of the hardware structures. For example, the maximum number of simultaneous data transactions that required for arithmetic operations determines the number of ALU ports. Also, communication channels between the ALU, accumulator, memories and IO must be assigned with specific data bus.

The execution of the control algorithm requires the repeated execution of a set of instructions (program). Although the number of instructions in the control loop can be small in the case of implementing a simple controller, the overhead that manipulate the program counter maybe relatively large. We therefore must pay special attention to the architecture of the program counter that implements control loops. Thus, the MPCSP can provide a looping mechanism that introduces a short, or ideally zero, overhead.

The final step is to create a hardware model that supports the operations needed to implement the control algorithm. This hardware model is programmed using the hardware description language. The resulted MPCSP is simulated and verified by running the MPC algorithm with the application-specific instructions. The MPCSP is then synthesized floor planned and placed & routed. The final net list can be verified via being downloaded into the FPGA and running the hardware-in-loop simulation.

Figure 2 shows the MPCSP architecture. It adopts a simple mixed data format in 2’s complement: the coefficients are in 12-bit floating point format, with 6-bit for mantissa and 6-bit for exponent. The state variables and other data are in 32-bit fixed point format, with 16 integer bits and 16 fractional bits. The memories include program ROM, data ROM and data RAM for control program, coefficients and intermediate states respectively. The sample timer is used to determine the sample interval for each control loop. The program counter processes one instruction at each clock cycle. It will halt the operation at the end of the control program, and reset to the address where the control loop starts at the rising edge of the sample timer.

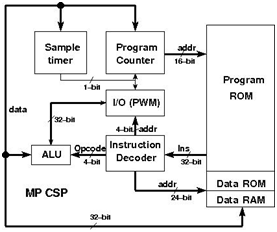
Figure 2 MPCSP architecture.

The MAC is the only processing element in the previous CSP design. Although this approach reduces the circuitry complexity, it is not efficient in terms of power and speed. Hence, in the MPCSP design, several processing elements are adopted for arithmetic operations as shown in Table 1. Each instruction uses the standard RISC convention of 32-bit fixed-length. All instructions have a single clock cycle execution.

The IO block has 12 inputs and 4 PWM outputs. The inputs are connected to the inertial sensors, including accelerometers, gyroscopes, magnetometers and sun sensors. The outputs are connected to the magnet coils through the power amplifiers. For attitude control, 3 magnet coils are needed to provide three-axis actuation.

The data bus and address bus of the MPCSP are connected to the AMBA to allow the general-purpose processor collect house-keeping data. The MPCSP is implemented targeting the Xilinx Virtex-4 FX100 FPGA technology. The MPCSP occupies less than 8% of the FPGA total area. It runs up to 120MHz. The power consumption is around 183 mW.

Simulation results

The simulating nano satellite operates at low Earth orbit altitude of 650km with an orbital inclination of 96° and has inertia matrix I=diag ([6.858e-4 6.858e-4 8.164e-4]). The MPC tuning parameters are listed in Table 2. We can see that in traditional MPC design, the control horizon ${\text{N}}_{\text{c}}$ is normally chosen to be more than 30 to get a sound control performance. While using Laguerre function, N can be selected as 5 to obtain the same performance, which means 6 times less parameters involved in on-line computation.

The control system is initialized at satellite pointing angles of $1^{\text{°}}$ about each axis and angular rates of 0.0005 rad/s about the roll, yaw and pitch axes.

The first set of simulation was carried out in Matlab, assuming no constraints on the control variables and the results are shown in Figures 3-5.

Figure 3 Attitude angles: simulation without constraints on the control torquers.

Figure 4 Attitude angular rates: simulation without constraints on the control torquers.

Figure 5 Magnetic torques: simulation without constraints on control torquers.

A second set of simulation was carried out in Matlab, with the constraints of Eqs. 27 and 28. The amplitude of the control torquers is $[-3\times {10}^{(-9)}N-m,3\times {10}^{(-9)}N-m]$ . The results are shown in Figures 6-8. As it can be seen in Figures 3-5, the simulation result violate the amplitude constraints, while the second set of simulations, the amplitude of control torque is successfully constrained within $\pm 3\times {10}^{(-9)}N-m.$ Obviously, due to the constraints on control torquers, it takes the system longer to come to the set points.

Figure 6 Attitude angles: simulation with constraints on the control torquers.

Figure 7 Attitude angular rates: simulation with constraints on the control torquers.

Figure 8 Magnetic torque: simulation with constraints.

Hardware-in-loop simulation

The MPC is then implemented on the MPCSP. A hardware-in-loop simulation platform as shown in Figure 9 is developed to test the control system processor. The MPCSP is implemented in a Virtex-4 FX100 FPGA board. The satellite attitude dynamics is modelled in C program in the computer. The PWM actuation signals from the FPGA board are sent to the computer using the industrial digital IO card. The feedback signals like angular rate are sent to the FPGA board using the analogue to digital converters.

Figure 9 Hardware-in-loop simulation for MPCSP.

Figures 10 & 11 show the results from the hardware-in-loop simulation. Compared to the Matlab simulation, in the difference is rather small. Hence the MPCSP is feasible for satellite attitude control using magnet torquers.

Figure 10 Attitudes: comparisons between hardware-in-loop simulation (Red) and Matlab simulation (Blue).

Figure 11 Attitude angular rates: comparisons between hardware in loop simulation (Red) and Matlab simulation (Blue).

A satellite magnetic controller is designed using Discrete-time Laguerre networks based MPC. Two sets of simulations are conducted on the same controller to compare its performance with and without constraints. From the results shown, the magnetic controller can lead to an impressive performance in satellite attitude control. With model predictive algorithm, it can successfully deal with hard constraints on control torquers. The MPC can greatly improve the stability of the satellite attitudes with small torques generated from the magnetorquers. This feature is important for small satellites as they normally cannot accommodate larger actuation devices, like thrusters, reaction wheels and so on.

A dedicated control system processor is developed to execute the MPC algorithm. The MPCSP can run upto 120MHz, while consuming 183mW and occupies less than 8% area of a Virtex-4 FX100 FPGA. The MPCSP is used to implement a model predictive attitude control law for a nanosatellite. The hardware-in-loop simulation shows that the MPCSP produces almost the same results as the Matlab simulation.

In future, the MPCSP will be applied in a student-built satellite mission, which is currently under investigation at the University of Sydney.

None.

Author declares that there is no conflict of interest.

1. CubeSat Kit, Pumpkin, Inc, San Francisco, USA.
2. G James Wells, L Stras, T Jeans. Canada’s Smallest Satellite: The Canadian Advanced Nanospace experiment (CANX-1). 2002. p. 1‒12.
3. AAU students has now started launch campaign on AAUSat. CubeSat. 2008.
4. Compass 1: CubeSat imaging project of the University of Applied Science at Aachen, Germany.
5. P Fortescue, J Stark, G Swinerd. Spacecraft Systems Engineering. 3rd edn. Wiley Press, USA; 2003. 704 p.
6. E Silani, M Lovera. Magnetic spacecraft attitude control: a survey and some new results. Control Engineering Practice. 2005;13:357‒371.
7. L Wang. Model Predictive Control System Design and Implementation using MATLAB. Springer Press, USA; 2009. 377 p.
8. Hovland S, Willcox K, Gravdahl JT. MPC for Large-Scale Systems via Model Reduction and Multiparametric Quadratic Programming. 45th IEEE Conference on Decision & Control. San Diego, USA; 2006. p. 3418‒3423.
9. W Chen, M Wood, D Fertin. Model Predictive Control of Low Earth Orbiting Spacecraft with Magneto-torquers. Proceedings of IEEE International Conference on Control Applications. Munich, Germany; 2006. 1‒8 p.
10. R Goodall, S Jones, R Cumplido Parra, et al. A control system processor architecture for complex LTI controllers. Proceedings of 6th IFAC Workshop AARTC. Palma de Mallorca, Spain; 2000. 167‒172 p.
11. RA Cumplido Parra. On the design and implementation of a control system processor. Ph.D. thesis, Loughborough University. 2001.
12. Xiaofeng Wu, Vassilios Chouliaras, Jose Nunez-Yanez, et al. A Novel Control System Processor and Its VLSI Implementation, IEEE trans. on VLSI. 2008;16(3):217‒228.
13. Xiaofeng Wu, Roger Goodall. 1-bit processing for digital control, IET Proc. Control Theory & Applications. 2005;152(4):403‒410.
14. K Stempak. Equiconvergence for Laguerre function series. Studia Mathematica. 1996;118(3):1‒9.
15. MJ Sidi Spacecraft dynamics and control. Cambridge University Press, Cambridge, UK, 403 p.
16. ML Psiaki. Magnetic Torquer Attitude Control via Asymptotic Periodic Linear Quadratic Regulation. AIAA Guidance, Navigation, and Control Conference. Denver, Colorado, USA; 2000.
17. AMBA Specification (Rev 2.0). ARM Limited, UK; 1999. 230 p.