The structural and dynamic features of the space (moving outside the dense layers of the atmosphere) stages of rockets - carriers of spacecraft as control objects are analyzed. The reasons are investigated - disturbing factors that generate external forces and moments that determine the disturbed motion of space rocket stages. For space rocket stages, disturbing factors are: mass asymmetry of the stage relative to its longitudinal axis and angle of mismatch of the line of action of the thrust vector of the propulsion system of the stage with the longitudinal axis of the stage. It is shown that when using the stage control deviating in the hinge of the marching engine as the executive organs of the control system, the effect of auto-reduction of the mentioned disturbing factors arises. The consequence of the auto compensation of disturbing factors is the reduction of disturbing forces and moments that violates the programmed motion of the step in the pitch and yaw planes. Mass asymmetry and the angle of mismatch of the line of action of the thrust vector of its engine and the longitudinal axis of magnitude are constant. Therefore, a decrease in perturbing forces and moments is accompanied by a decrease in the amount of energy (fuel) spent on processing (zeroing) perturbations of the parameters of the perturbed motion of the stage. It is shown that if the thrust of a space-stage engine is 8000 kgf, the engine operating time (flight time of the stage) is 500 sec, the specific engine thrust is 330 sec, the mass asymmetry is 0.05 m, the angle of mismatch is 0.25 degrees, then fuel economy can reach 200 kgf. The studies were performed using mathematical modeling methods.

Keywords: control ability, motion stability, energy consumption

The flight of space stages of launch vehicles (LV) occurs outside the dense layers of the atmosphere, therefore, its perturbed motion is formed only by perturbing forces and moments caused by the mass asymmetry of the stage relative to the longitudinal axis and errors in the manufacturing, assembly, installation of the stage and its propulsion system. Mass asymmetry of space steps is peculiar to rockets; it is not a random value - determined and measured under the conditions of manufacture of the launch vehicle.

Errors in the manufacture, assembly and installation cause the skewness of the line of action of the thrust vector P of the propulsion system of the stage relative to the longitudinal axis of the stage; skew - a random variable. Mass asymmetry and distortion are caused by the presence of disturbing effects on the movement of the LV stage and the need for additional fuel costs to work out the perturbations of the motion parameters.Modern rockets are perfect dynamic systems, but the possibilities for their improvement are not yet exhausted. Thus, the duality of the role of the parameter -"the incompatibility of the center of mass of the rocket stage with the line of action of the vector P-the traction of its marsh engine" is not taken into account yet. On the one hand, -the perturbing factor is the cause of the perturbation of the rocket stage motion, and on the other hand, - factor  the stage motion control; if the control is implemented by swinging the main engine in the hinge. The duality of the role is the ability to minimize the energy (fuel) costs for working out perturbations of the carrier motion parameters.

The purpose of research

Identification and ustification of areas for improvement of launch vehicles.

Research methods

Analytical analysis and mathematical modeling of control processes and stability of the unperturbed motion of the stages of rockets-carriers of spacecraft.

The research results relate to the problem of a rational choice of the executive bodies of the spacecraft stage control system of the launch vehicle. Consider the motion of the space stage of a carrier rocket, which is controlled by a roll of engine of small thrust, and by pitch and heading, by a mash engine. Pitch and course control is achieved by deflecting the vector P of the traction force of the marching engine of the space stage in the planes xoy, xoz of the associated coordinate system¹ from its longitudinal axis by angles ${\gamma }_{\vartheta },{\gamma }_{\psi }$ , respectively.

Figure 1 & 2 contain diagrams that illustrate the action of forces and moments of force on the LV stage when the vector P deviates from the longitudinal axis of the space stage of the nostel rocket.²

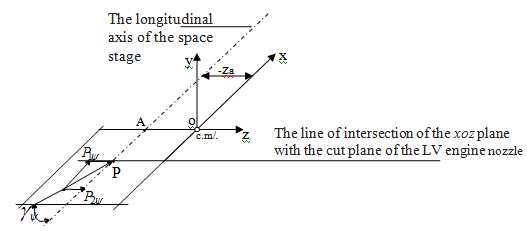
Figure 1 Scheme of action on the space step of the force P in the xoz plane related coordinate system.

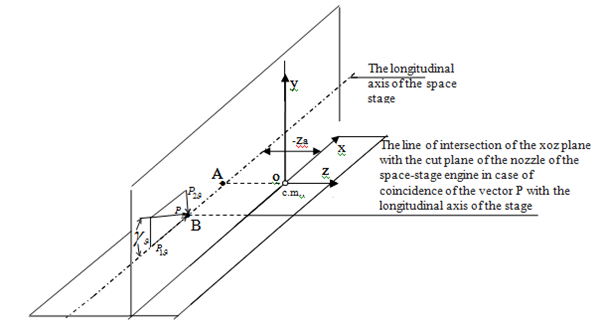
Figure 2 Scheme of action on the space stage of the engine thrust P in the xoy plane related coordinate system.

On the diagrams: OXYZ-a linked coordinate system, a с.m. is the center of mass of the stage, (-$-Z_a$ ) is the mass asymmetry value (it is assumed that the center of mass of the stage coincides with the point of the negative half-plane; <0, (Figure 1);

${\gamma }_{\psi }$ -the angle of deviation of the vector P from the plane parallel to the plane XOY and such that it passes through the longitudinal axis of the stage. The force P (when asymmetry $Z_{\text{а}}$ and angle ${\gamma }_{\psi }$ are obvious) forms a moment ${\overline{M}}_{oy}=-P_1\cdot \left|Z_{\text{a}}\right|+P_2\cdot (l_{п}-x_{Т})$ around the axis $OY$ , the vector of which is directed along the axis $OY$ . Component- $-P_1\cdot Z_{\text{a}}=-Р\cdot \mathrm{Cos}({\delta }_{\psi })\cdot \left|Z_{\text{a}}\right|$  is disturbing moment; component $P_{2\vartheta }\cdot (l_{п}-x_{Т})=P\cdot \mathrm{Sin}\left({\delta }_{\vartheta }\right)\cdot \left(l_{п}-x_T\right)$ is moment, which may be the moment controlling.

Usually, angle $\left|{\gamma }_{\psi }\right|\le 5^0$  and $P_1\approx Р,P_2\approx P\cdot {\gamma }_{\psi }.$  Note, that a $P_1={Р}_1(t),P_2=P_2(t)$ are functions of time.  The non-stationarity $P_1$  is caused by the non-stationarity of a parameter $Z_{\text{a}}$ , that changes in time due to the emptying in flight of the fuel tanks of the space stage of the launch vehicle (a process independent of the control system), while the non-stationarity $P_2$ depends on the angle ${\gamma }_{\psi }$ , which varies in accordance with the control commands.

Figure 2 shows that P, in the presence of an asymmetry $Z_{\text{a}}$ and an angle ${\gamma }_{\vartheta }$ , forms around the axes $OY,OZ$   moments ${\overline{M}}_{oy}=-P_{1\vartheta }\cdot Z_a$ , ${\overline{M}}_{oz}=P_{2\vartheta }\cdot (l_{п}-x_{Т})$ .

The components  $P_{2\psi },P_{2\vartheta }$   of the vector P (Figure 1-3) act in a plane parallel to the plane $YOZ$ .

From Figure 3 it follows that the component of the force P creates a moment ${\overline{M}}_{x\varphi }=-P_{2\vartheta }\cdot Z_{\text{a}}\approx -P{\gamma }_{\vartheta }\cdot Z_{\text{a}}$ . If the center of mass of the stаge does not coincide with the point of the plane $XOZ$ , then the force $P_{2\psi }$ also creates a moment around the axis $OX$ .

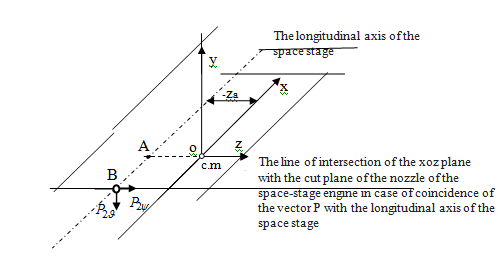
Figure 3 Scheme of action on the LV stage of components P, which create moments of forces around the longitudinal axis.

The components $P_{1\psi ,}{P}_{1\vartheta }$ of the moments of forces around the axis $OX$ do not create. An analysis of Figure 1& 2 shows that the swing of the vector P around the point of the longitudinal axis of the LV stage, when the mass asymmetry of the stage is obvious, creates moments of forces around the center of mass of the stage, which can be used to control the movement of the stage along pitch, heading, and roll. As an example, to illustrate what was skozhennogo, the effect of the application of the proposed method when controlling the movement of the 3rd stage of the modern launch vehicle with the following characteristics is considered.³

1. The rated thrust of the main engine in the void is 7916 kgf,
2. Shift of the geometric axis of the engine chamber relative to the axis of the frame, mm, not more than 2;
3. Deviation of the axis of the engine chamber from the perpendicular to the plane of the junction of the engine with the frame, under load, not more than 15 arc minutes (~25 arc degrees).
4. Mass asymmetry, m, not more than: - at the beginning of the movement $y_T$ =0.003, $z_T$ =0.0085,

at the end of the movement $y_T$ =0.017, $z_T$ =0.05.

5. Central principal axial moments of inertia: -at the beginning of the movement $I_x=307,I_y=I_z=1189$  

at the end of the movement $I_x=306,I_y=I_z=\mathrm{310.5.}$

6. The shoulder of the control forces in pitch, heading, m:
   1. at the beginning of the movement $l_{упр}=11.281$ ,
   2. at the end of the movement   $l_{упр}=10.966$ .
7. The distance of the center of mass of the step from the longitudinal axis the:
   1. in the beginning of the movement $z_a=0.01,$
   2. at the end of the movement $z_a=0.05$ .
8. The distance of the center of mass of the step from the tip of his nose, m:
   1. at the beginning of the movement $x_{Т}=1.819$ ,   
   2. at the end of the movement $x_{Т}=2.034$ .
9. The duration of the perturbed movement of the stage: 470 s.
10. The total length of the stage launch vehicle, m:13.

The step control (standard option) in pitch and course is provided by swinging the combustion chamber of the marching engine in the planes of the associated coordinate system,¹ in roll by jet thrust engines that create the thrust moment vector directed along the longitudinal axis of the stage. Mathematical modeling of the process of controlling the angular movement of the third stage of a modern launch vehicle,³ that is controlled by pitch and heading by swinging the vector P, was performed using the MathCad software package for a PC. The mathematical model of the motion of the space stage of the launch vehicle was built taking into account unsteady masses, moments of inertia, coordinates of the central masses, and parameters of the motion of the stage.

Models of unsteady characteristics, parameters, disturbing and controlling moments of forces were written as

$\begin{array}{l}{Z}_{а}=-0.01-\frac{0.04\cdot t}{470}м,I_x=306кгс\cdot м\cdot {с}^2,\\ I_y=I_z=1189-\frac{878.5}{470}\cdot tкгс\cdot м\cdot {с}^2,\\ x_T(t)=1.819+0.215\cdot {470}^{-1}.\end{array}$

${\overline{M}}_{зdis}^{\psi }=\frac{P\cdot [Z_a+{\gamma }_{\psi }\cdot (x_{п}-x_{Т})]}{(1189-\frac{878.5}{470}\cdot t)}\text{}{s}^{-2},$  ${\overline{M}}_{dis}^{\varphi }=\frac{P\cdot \frac{0.25}{57.3}\cdot (0.01+\frac{0.04}{470}\cdot t)}{306}{s}^{-2}$   

${\overline{M}}_{cont}^{\psi (\vartheta )}=\frac{P\cdot (11.181-\frac{0.218}{470}\cdot t)}{(1189-\frac{878.5}{470}\cdot t)}\cdot {\gamma }_{\psi (\vartheta )}{s}^{-2}\cdot rad,$  ${\overline{M}}_{cont}^{\varphi }=\frac{P\cdot (-0.01-\frac{0.04}{470}\cdot t)}{306}\cdot {\gamma }_{\varphi }{s}^{-2}rad.$   

Here are ${\overline{M}}_{ccont}^{\psi (\vartheta )},{\overline{M}}_{cont}^{\varphi }$ the control moments for the course (pitch), roll; ${\overline{M}}_{dis}^{\varphi },{\overline{M}}_{cont}^{\varphi }$ -disturbing, controlling moments on the roll; $\vartheta ,\psi ,\varphi$ - perturbations of pitch angles, course, roll, respectively; $Y_a{Z}_a$ is the distance from the center of the mas stage to the planes xoz, xoy, respectively; ${\gamma }_{\psi },({\gamma }_{\vartheta })$  is the angle between the projection of the vector P on the plane xoz (xoy) and the axis ox.

The initial data for the simulation was recorded on the Mathcad worksheet as follows: $x^T=\left|0.03000.0200\right|$ , P:=7916, K0:=0.5, K1:=0.25, K01:=0.5, K11:=0.2, T:=0.01. Here K0, K1, K01, K11 are the transfer coefficients, T is the time constant of the control system, - the state vector is transposed. The function D (t, x)-the function of calculating the first derivatives was written in the form:

$D(t,x):=\left[\begin{array}{c}\begin{array}{c}{x}_1\\ P\cdot \left(1181-5.319\times {10}^{-4}\cdot t\right)\cdot \frac{\left(5.319\times {10}^{-4}-x_2\right)}{1181-1.871\cdot t}\\ \frac{\left(K0\cdot x_0+K1\cdot x_1-x_2\right)}{T}\end{array}\\ x_4\\ \begin{array}{c}P\cdot \left(0.01+0.04\cdot \frac{t}{470}\right)\cdot \frac{\left(4.363\times {10}^{-3}-x_5\right)}{306}\\ \frac{\left(K01\cdot x_3+K11\cdot x_4-x_5\right)}{T}\end{array}\end{array}\right]$

$Z:=rkfixed(x,0,100,100000,D)$ -team for mathematical modeling.

Character Mappings Introduced: $\vartheta :=x_0,\dot{\vartheta },:=x_1,{\gamma }_{\vartheta }:=x_2,\varphi :=x_3,\dot{\varphi }:=x_4,\text{}{\delta }_{\varphi }:=x_5$

From Figure 4-6 it follows: the initial perturbations $\vartheta (0)=0.03rad,\dot{\vartheta }(0)=0.03rad/s,\varphi (0)=0.02rad$ of the parameters of the stage motion are worked out quite qualitatively.

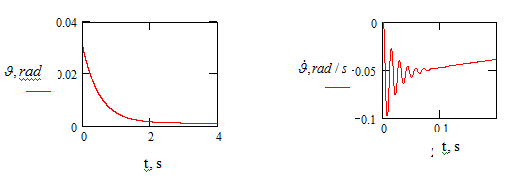
Figure 4 Time variation of perturbations of the step motion parameters.

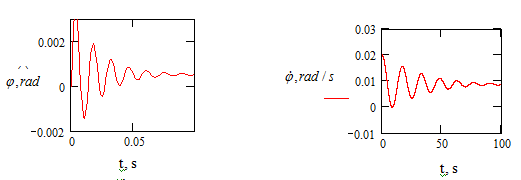
Figure 5 Time variation of perturbations of the step motion parameters.

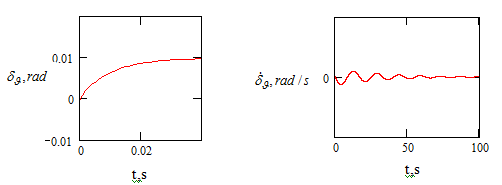
Figure 6 Time variation of perturbations of the stage motion parameters.

Let us carry out a simplified analytical and further refined numerical analysis of the processes of working out disturbances of the parameters of the stage motion by swinging the marching engine and compare them with the processes of working out disturbances by steering engines in two in the pitch and course channels.

 In the case of a simplified analysis, it is permissible to use the method of “frozen” coefficients and the principle of superposition, which are often used in problems of rocket dynamics.^1-3 Let us consider separately the processes of developing perturbations of the parameters of the motion of space stages of the LV from mass asymmetry and skew line of action of the vector P of the thrust of the main engine of the stage relative to its longitudinal axis due to errors in the manufacture, assembly, installation of the stage and its propulsion system.

We write the mathematical models for working out perturbations in the form:

- Equations (1, 2) when controlling the swing stage in the hinge of the mid-flight engine

 $\{\begin{array}{l}{I}_{y(z)}\cdot \frac{d^2\psi }{d{t}^2}=P\cdot Z_a-P\cdot {\gamma }_{упр}\cdot (l_{п}-x_{Т}),\\ T\cdot \frac{d{\gamma }_{упр}}{dt}+{\gamma }_{упр}=k_0\cdot \psi +k_1\cdot \frac{d\psi }{dt}.\end{array}(1)$   $\{\begin{array}{l}{I}_{y(z)}\cdot \frac{d^2\psi }{d{t}^2}=P\cdot {\gamma }_{зб}\cdot (l_{п}-x_T)-P\cdot {\gamma }_{упр}\cdot (l_{п}-x_{Т}),\\ T\cdot \frac{d{\gamma }_{упр}}{dt}+{\gamma }_{упр}=k_0\cdot \psi +k_1\cdot \frac{d\psi }{dt}.\end{array}(2)$  

- Equations (3, 4) when controlling a stage with steering engines

 $\{\begin{array}{l}{I}_{y(z)}\cdot \frac{d^2\psi }{d{t}^2}=P\cdot Z_a-2\cdot P_{упр}\cdot (l_{п}-x_{Т})\cdot \delta ,\\ T\cdot \frac{d\delta }{dt}+\delta =k_0\cdot \psi +k_1\cdot \frac{d\psi }{dt}.\end{array}(3)$   $\{\begin{array}{l}{I}_{y(z)}\cdot \frac{d^2\psi }{d{t}^2}=P\cdot {\gamma }_{зб}\cdot (l_{п}-x_T)-2\cdot P_{упр}\cdot (l_{п}-x_{Т})\delta ,\\ T\cdot \frac{d\delta }{dt}+\delta =k_0\cdot \psi +k_1\cdot \frac{d\psi }{dt}.\end{array}(4)$  

In equations 1-4, the angles of deviation of the line of action of the thrust vector P of the marching engine thrust from the longitudinal axis of the stage, due to errors in the manufacture, assembly, installation of the foot, its propulsion system (excitation factor) and due to the control commands of the control system, aimed at working out perturbations of the stage motion parameters respectively; $\delta$ - the angle of deviation of the steering engine from the neutral position in accordance with the commands of the stage control system, aimed at working out perturbations of the motion parameters.

In steady-state modes of motion, the values $\ddot{\psi },\dot{\psi }$ ​​ are zero and we obtain:

1). ${\gamma }_{cont}=\frac{Z_{а}}{(l_{п}-x_T)}={\gamma }_{dis}$ -from the of equations  (1), and ${\gamma }_{cont}={\gamma }_{dis}$ -from the equations of system (2).

2). $\delta =\frac{P\cdot Z_a}{2\cdot P_{cont}(l_{п}-x_T)}$ , $\delta =\frac{P\cdot {\gamma }_{зб}}{2\cdot P_{уcont}}$  - from equations of systems (3), (4), respectively.

Thus, when controlling the movement of a stage by swinging the main engine, the zeroing of disturbances in the parameters of the stage motion is achieved by reducing the disturbing factors by turning the main engine in a hinge. The refined numerical analysis of the processes of working out the disturbances of the motion parameters by swinging the main engine and steering engines is carried out according to the results of mathematical modeling of the stage stabilization processes using the Mattcad programs.

Initial data:

$P:=7916кгс,T:=0.01c,L:=11м,K0:=1,K1:=0.25c,x:=\left|\begin{array}{c}0.03\\ 0\\ 0\end{array}\right|$ ,

 $D(t,x):=\left[\begin{array}{c}{x}_1\\ P\cdot \frac{\left[\left(0.01+1\cdot {10}^{-4}\cdot t\right)-L\cdot x_2\right]}{1190-880\frac{t}{400}}\\ \left(K0\cdot x_0+K1\cdot x_1-x_2\right)\cdot T^{-1}\end{array}\right]$   $Z:=rkfixed(x,0,100,100000,D)$  

At characteristic times, the control parammeter ${\gamma }_{упр}$ takes values

${\gamma }_{cont}(t=0.12)=5.99\cdot {10}^{-3}rad,{\gamma }_{cont}(t=100)=6.364\cdot {10}^{-3}rad.$

The results of modeling the processes of stabilizing the movement of the LV stage by steering engines

Initial data: К0=:0.1   К1=:0.5   Т=:0.01     а=:1000 $x:=\left(\begin{array}{c}0.03\\ 0\\ 0\end{array}\right)$  

 $D(t,x):=\left[\begin{array}{c}{x}_1\\ \frac{\left[\left(0.01+1\cdot {10}^{-4}\cdot t+0.05\right)\cdot P-2a\cdot x_2\right]}{1190-880\frac{t}{400}}\\ \left(K0\cdot x_0+K1\cdot x_1-x_2\right)\cdot T^{-1}\end{array}\right]$   $Z:=rkfixed(x,0,100,100000,D)$  

The control parameter $\delta$ takes the following values ​​at characteristic times

$\delta (t=20)=0.243rrad,\delta (t=100)=0.277rad.$

The amount of energy required for working out perturbing effects on the movement of the LV stage during a 100s flight when using a marching engine is characterized by an estimate

$Q_{\gamma }=P\cdot {\displaystyle \underset{0}{\overset{100}{\int }}{\gamma }_{cont}(t)dt}$ ,

when using steering engines ( $P_{cont}=1000kgf$ ) characterize the value

$Q_{\delta }=2\cdot P_{cont}\cdot {\displaystyle \underset{0}{\overset{100}{\int }}\delta (t)dt.}$

The values ​​of the integrated estimates of energy costs, determined from the presented results of mathematical modeling, are as follows:. $Q_{\gamma }=49.957kgf\cdot rad\cdot s,Q_{\delta }=41.6\cdot {10}^3кkgf\cdot rad\cdot s$ .

An examination of the processes (Figures 7–10) of testing the disturbances of the parameters of the LV stage motion, analysis of the results of mathematical modeling of these processes show the following:

1. The main engine as the executive body of the spacecraft stage control system of the LV with mass asymmetry relative to the longitudinal axis provides stage control with a reduction in the influence of disturbing factors,
2. The effect of decreasing the value of the perturbing factor is accompanied by a decrease in the amount of energy (fuel) necessary for working out perturbations of the parameters of the LV stage motion.

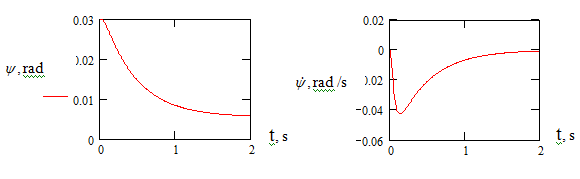
Figure 7 Time variation of perturbations of the stage motion parameters $\psi$ , $\dot{\psi }$ .

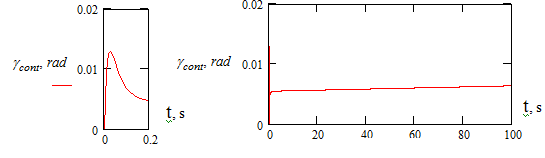
Figure 8 Hafiki time variation of the control parameter $x_2={\gamma }_{cont}$ .

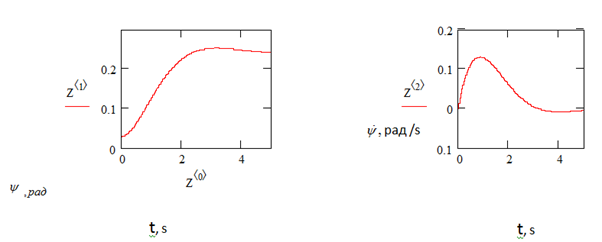
Figure 9 Time variation of perturbations of the stage motion parameters $\psi$ , $\dot{\psi }$ .

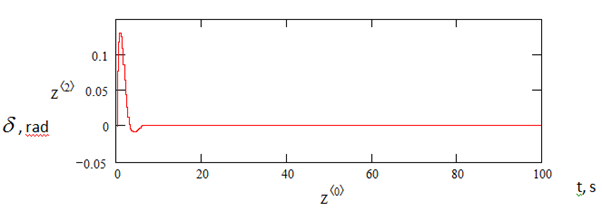
Figure 10 Gaifik changes in time of the control parameter $\delta$ .

The implementation of the effect of the reduction of disturbing factors is a possible direction for improving the space stages of the LV as an object of control.

None.

Authors declare that there is no conflict of interest.

1. Gerasyuta NF, Novikov AV, Beletskaya NG. Flight dynamics: The main pillars of the dynamic design of missiles. Dnepropetrovsk; 1998.
2. Igdalov IM, Kuchma LD, Polyakov MV, et al. Rocket-launch and space launch rockets of yak ob'kti keruvannya. Dnipropetrovsk, Vidavnitsvo DNU; 2007.
3. Igdalov IM, Kuchma LD, Polyakov MV, et al. Dynamical project of missile launch. Dnipropetrovsk, Vidavnitsvo DNU; 2010.