Electrical charge is considered in complex domain. The potential and the interaction force of complex charges have been obtained. A quanton, featuring a sum of elementary charges of electron and proton represented in complex form, has been formulated as an elementary particle of physical vacuum. The structure of the physical vacuum, consisting of non-interacting neutral quantons with electrical and magnetic moments randomly distributed in space, has been determined. The interaction of moving charged particles in a physical vacuum has been considered. Theoretical calculation of the energy and the electron spin rotation velocity has been performed.

Keywords: complex charge, quanton, physical vacuum, magnetic charge, electron spin

The experimental determination of the rotation of electrons in an atom around their own axes was made by Otto Stern and Walther Gerlach in 1922. Stern-Gerlach experiments are based on the fact that the flow of particles featuring magnetic moments must be deflected in a non-uniform magnetic field due to the interaction of the magnetic moments of the atom with the intensity gradient of the external magnetic field.

The atoms of alkali metals and silver atoms with valence electrons in s-state featuring no orbital magnetic moment were used in the experiments. A valence electron in this state possesses only its own mechanical moment-spin–and, appropriately, a magnetic moment. If no restrictions are imposed onto the angle between the magnetic moment and the external magnetic field, then after the stream of atoms passed through the region of inhomogeneous magnetic field, a broad band of atomic particles would be observed. However, in reality, two narrow strips are formed, symmetrically located in reference to the trace which is produced when the magnetic field is turned off. This bifurcation is explained by the fact that in this case the magnetic moment of an atom can be oriented in accordance with spatial quantization only either parallel to or antiparallel to the field. The magnetic moment of an atom, equal to the electron magnetic moment, was determined based on the distance between the spots. The magnetic moment turned out to be in good agreement with the Bohr magneton for all atoms under study.

The Bohr magneton is an integer number for the orbital magnetic moments of the atoms of other elements. The relationship between the mechanical and magnetic moments for the orbital motion of the electrons in an atom is expressed by the following formula:

$\mu =\frac{e}{2m_{e}c}M$ (1)

Where $M=\frac{h}{2\pi }\sqrt{l\left(l+1\right)}$ is the mechanical moment while l is the azimuthal quantum number and h is Planck's constant. It is derived from (1): ${\mu }_0=\frac{eh}{4\pi m_e}=928.477\cdot {10}^{-26}J\cdot T^{-1}$ – Bohr magneton.

In 1925, George Uhlenbeck and Samuel Goudsmith purely formally introduced a concept of the electron’s own mechanical moment; according to the concept an electron rotating around its axis possesses its own mechanical moment. G. Uhlenbeck and S. Goudsmith determined this mechanical moment it by analogy with the orbital motion in the following form:

$M_e=\frac{h}{2\pi }\sqrt{S_e\left(S_e+1\right)}$ (2)

where they presented the spin quantum number in the form: S_е =1/2

Consequently, the electron state in an atom does not matter; the electron possesses a mechanical moment, that is, a spin of a constant value, in all states. The concept of “by analogy” is not physically justified, however, it made it possible to explain the multiplet structure of atomic spectra and their features in electric and magnetic fields. Therefore, the assumption of a constant value of the electron mechanical rotational moment in all atomic states has been firmly established in quantum mechanics, however without analyzing the reasons of this behavior of electrons. In this connection, the following goal shall be set: to consider in detail the structure of the physical vacuum, and to find out what interactions arise when charged particles move in the physical vacuum. To reach the goal it is sufficient to solve the following problems:

1. To consider the interaction of electric charges in the most general form, representing the charges in complex form.
2. To justify the structure of the physical vacuum in complex space.
3. To determine the nature of the interaction of charged particles as they move in the physical vacuum.

Let us consider, one after another, these problems

Analyzing electrodynamics from the standpoint of the relativistic theory of relativity, Dirac arrived at the conclusion about the full symmetry of the surrounding world and, with the aim to complete this symmetry, introduced a magnetic charge, calling it a monopole. However, remaining within the framework of the real four-dimensional world he did not manage to present the correct interpretation of the complete symmetry of the world around us. Full symmetry should be interpreted not from the standpoint of the mutual transformation of electrical and magnetic interactions, but from the point of view of strict symmetry with respect to the speed of propagation of electromagnetic oscillations, that is, with respect to the speed of propagation of light. Such symmetry is presented in Figure 1 in the form of Eight-Dimensional World. Both worlds interact with each other and exist in a fairly strong relationship.

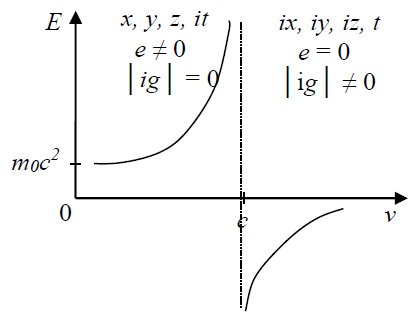
Figure 1 General picture of eight-dimensional world.

In this picture, the world around us has real space and imaginary time, which moves forward. Electric charges really exist. The speed of light is not achievable for really moving masses and charges. In the area where the speed of movement is higher than the speed of light, the space is imaginary while time is real and moves backward. Electric charges are imaginary and non-zero. The speed of light in such a world is also not achievable. Particle energy is negative. It increases as the speed increases and tends to zero, as shown schematically in Figure 1. Therefore, in nature, the world is not four-dimensional, but eight-dimensional one. In the eight-dimensional World the resulting charge should be presented in complex form, i.e.:

$Q=e+ig$ (3)

The interaction energy between the point charges is determined by the product of these charges and is inversely proportional to the distance between them that is, in accordance with Coulomb's law. In general, the interaction energy takes the following form:

$U=k\frac{Q_1{Q}_2}{r}$ (4)

where k is the proportionality coefficient determined by the chosen system of units of measurement and r-is the distance between the interacting charges which is represented in complex domain as

$r=\left|r\right|\left(\cos \phi +i\sin \phi \right)$ (5)

Equation (4) is applicable to point charges and should be viewed as the force interaction of Q2 charge in the force field created by Q1 charge.

After having performed multiplying and dividing the complex numbers in (4), we obtain the following expression for the real part of the interaction energy:

$\mathrm{Re}U=k\frac{\sqrt{{\left(e_1{e}_2-\chi g_1{g}_2\right)}^2+{\left(\sqrt{\chi }{g}_1{e}_1+\sqrt{\chi }{g}_2{e}_2\right)}^2}}{r}\cos \left({\phi }_1-{\phi }_2\right)$ (6)

where φ₁ and φ₂ are the arguments of the numerator and the denominator, е₁, е₂, g₁ and g₂ are, correspondingly, the real charges and the real part of the imaginary charges of mutually opposite signs while factor χ has been introduced to match the systems of units of measurement of the real electric charges and the imaginary ones.

In the first rough approximation, due to cross-interaction φ₁≈φ₂ and $\frac{1}{2}{\left(\frac{\sqrt{\chi }{g}_1{e}_1+\sqrt{\chi }{g}_2{e}_2}{e_1{e}_2-\chi g_1{g}_2}\right)}^2<<1$ . Then equation (6) is converted to the following form:

$\mathrm{Re}U=k\frac{e_1{e}_2}{r}-k\frac{\chi g_1{g}_2}{r}$ (7)

i.e., the potential energy of interaction of generalized complex charges is equal to the sum of the interaction energies of real electric and imaginary charges, which can be separated both in space and in time. The obtained interaction potential coincides, in form, with Weber potential, which reflects Coulomb law in the process of separation of electric charges along a certain radius-vector as they move, that is, when the interacting charges approach each other or diverge from each other. Comparing potential (7) with Weber potential, we obtain the following equations

$g_1=e_1{v}_1 and g_2=e_2{v}_2$ (8)

The product of the charge and the speed of its movement, according to Sommerfeld, should be regarded as a magnetic charge. As a matter of fact, equations (8) are the manifestations of imaginary charges in real space and imaginary time, and in absolute terms they are magnetic charges. Therefore, all equations that describe electrostatic field have the same form for magnetostatic field.¹

If we take the derivative of (7) with respect to the radius-vector r, then we obtain the interaction force taking into account the motion of the complex charges, namely:

$F=k\frac{e_1{e}_2}{r^2}-k\frac{\chi g_1{g}_2}{r^2}$ (9)

Equation (9) was written by Hendrik Lorentz without any developments of mathematical expressions based on general concepts; the equation bears his name: Lorentz equation. Actually, equation (9) represents the force of interaction of complex charges.

Physical vacuum is formed by collapsed electron-positron pairs. A collapsed electron-positron pair in the complex space presents a quanton.¹ This means that the electron and positron in the quantum are represented as two complex charges:

$e^{-}=e_{-}+i{g}^{-} and e^{+}=e_{+}+i{g}^{+}$ (10)

Figure 2 shows a single quanton. Inside the quantum, real bunches of energies of different signs rotate relative to each other at the speed of light. Imaginary charges also rotate at the speed of light. According to this model representation, the magnetic moment of an individual quanton:

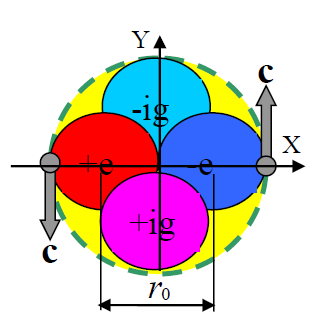
Figure 2 Layout of a single quanton.

$p_{m,0}=igi{r}_0=-ce{r}_0$ (11)

i.e. is a real one.

If an external magnetic field is imposed on the quantum, the magnetic moment of the quantum is set along the external field, since the quantum is an absolutely free particle. A perturbation of the physical vacuum occurs. As this takes place, the magnetic moments of all quantons line up along the magnetic induction force lines.

When the charges of different signs approach each other close enough, they mutually compensate their charges and so their force fields are leveled. Under such conditions, the charges of different signs form a collapsed massless particle in the form of a bunch of energy fields of different nature. Collapsed real and imaginary charges form physical vacuum (or ether, as it was conventional to consider before Dirac). Figure 2 shows schematically a particle of physical vacuum without mass. The real charges are located along the positive X-axis while the imaginary charges are located along the imaginary Y- axis. In this case, the imaginary positive charge is coupled with the positive real charge, while the imaginary negative charge is coupled with the real negative charge.

The charges of different signs cannot remain in statics. Therefore, they have to perform a rotational motion relative to each other in the quantum. The quantons do not interact with each other, but create a close-packed structure, which presents physical vacuum. When external fields created by free real or magnetic charges act on the physical vacuum, a deformation of the physical vacuum occurs due to the polarization of real and, accordingly, imaginary charges. In the process, real electric dipoles and dipoles of imaginary charges, i.e., magnetic dipoles appear. Under substantial polarization of the physical vacuum, electron-positron pairs are born. Both the polarization of vacuum particles and the birth of electron-positron pairs occur under the action of weak interactions. On this basis, the real charges create an electric field and represent electric charges while the imaginary charges create the energy field which should be considered as magnetic field.

In the light of these considerations let us we investigate the nature of real electric and imaginary magnetic charges separately. In doing so it should be taken into account than that minimum electric charge existing in the nature is an electron to which negative sign is assigned, and a positron possessing minimum positive charge equal in magnitude to the electron charge. Minimum magnetic charge is the Dirac monopole, which cannot be measured, since it is imaginary. Real electric charges appear as a result of the birth of electron-positron pairs under the influence of the absorption by vacuum of two photons of hard electromagnetic radiation. When Arnold Sommerfeld² calculated the energy of the electric field generated by the charge of a resting electron, he obtained that the energy of the electric field of the electron amounted to only 3/4 of the energy of the electrodynamic mass of the electron while one fourth of that must be of a different origin, i.e., the interaction energy of imaginary magnetic charges. In order not to violate the law of conservation of energy, it was necessary to introduce a hypothetical particle–an electron neutrino-into the reaction of the formation of electron-positron pairs.

If we consider the vacuum as a state of electron-positron collapsed electric charges, then, under the influence of external electromagnetic field, such medium must undergo a deformation, i.e. it must polarize with the formation of an electric dipole. Some work is spent on doing that. Consequently, the energy of a charged body according to Faraday is not contained in the magnitude of the charge, but in the field. In reality, not a field, but the medium is polarized and presents a carrier of the energy of a charged body. We wish we could have understood it earlier!

The particles smallest in mass and charge-electron and positron–feature an interesting property. When these particles get in touch with each other at the distance equal to their radius, the collapse occurs. In this state, their gravitational mass turns into an electromagnetic energy bunch which is able to get polarized, under the influence of external electric or magnetic field, and to absorb electromagnetic energy. If the polarization exceeds a certain critical size between the charges under the action of an electromagnetic field, then two particles are again born with equal gravitational masses and with equal charges of different signs. If the polarization is caused by a moving charged particle - electron or positron - the exchange between the quantum and the moving particle occurs. In this case, a new quantum is born, and the particle, which belonged to the initial quantum, further continues its movement. As this takes place, the laws of conservation of energy and momentum are not violated, but in the process of interaction with the whole set of quantons of the physical vacuum, a scattering occurs, that is, a diffraction phenomenon occurs in unordered structure.

The following dependence follows from the strict symmetry of the surrounding world: $eg=n\frac{hc}{4\pi }$ where $n=0,\pm 1,\pm 2,\mathrm{...},$ while е and g present, respectively, unit electric and magnetic charges. Such a relationship does not contradict the fundamental principles of quantum mechanics, but is not a justification for the essence of the strict symmetry of the surrounding world. When neutral particles move in the vacuum, the kinetic energy of the particles is not lost but when charged particles move due to the vacuum polarization, the kinetic energy of the particles decreases. During the flight of spacecraft that use plasma or ion engines, they are charged with a positive or negative charge. In this case, there is a noticeable vacuum friction. Let us consider this process in more detail.

When neutral particles move in the vacuum, the kinetic energy of the particles is not lost but when charged particles move due to the vacuum polarization, the kinetic energy of the particles decreases. During the flight of spacecraft that use plasma or ion engines, they are charged with a positive or negative charge. In this case, there is a noticeable vacuum friction. Let us consider this process in more detail. Let a spherical particle of radius R, possessing a charge q, move in vacuum with velocity v. Such particle creates a spherically symmetric electric field, and this field polarizes the quantons of the physical vacuum. As a result, each quanton is polarized within the element of spherical volume $4\pi r^{2}dr$ situated at the distance r from the particle. In this case, the external force is compensated by the internal force of the interaction of the electron with the positron. Then:

$e{E}_{\theta }=\frac{e^2}{4\pi {\epsilon }_0{r}_0^2}-\frac{e^2}{4\pi {\epsilon }_0\left(r_0+\Delta r\right)}=\frac{2e^2\Delta r}{4\pi {\epsilon }_0{r}_0^3}$ (12)

Here $r_0\cong 1.41\cdot {10}^{-15}$ (m) is the distance between electron and positron in quantum, $E_{\theta }=q/4\pi {\epsilon }_0{r}^2$ - is the field strength created by a moving charged particle at the distance of r, and

$\Delta r=\frac{q}{2e}\frac{r_0^3}{r^2}$ (13)

As a result, an electric dipole is formed inside one quanton $p_{\theta }=e\Delta r$ . The energy spent to create such dipole will

amount to:

$\Delta U=-p_{\theta }{E}_{\theta }$(14)

This energy increases due to the electron-dipole interaction and decreases due to the dipole-dipole interaction between electric charges and induced dipoles. Therefore

$\Delta U_{pe3}=-p_{\theta }{E}_{\theta }-\frac{e{p}_{{}_{\theta }}}{4\pi {\epsilon }_0{r}^2}+\frac{2p_{{}_{\theta }^2}}{4\pi {\epsilon }_0{\left(2r_0\right)}^3}$ (15)

The spherical layer situated at the distance r from the moving charge contains the following number of quantons:

$N_{k\theta }=\frac{4\pi r^{2}dr}{8{\left(a+r_0/2\right)}^3}$ (16)

Here $a=2.818\cdot {10}^{-10}$ (m) presents the classical electron radius.

The work spent on vacuum polarization around a moving charged particle is equal to

$A={\displaystyle \underset{R}{\overset{\infty }{\int }}\left(-\frac{q{r}_0^2}{2r^2}\frac{q}{4\pi {\epsilon }_0{r}^2}-\frac{e{p}_{{}_{\theta }}}{4\pi {\epsilon }_0{r}^2}+\frac{2p_{{}_{\theta }^2}}{4\pi {\epsilon }_0{\left(2r_0\right)}^3}\right)}\frac{4\pi r^{2}dr}{8{\left(a+r_0/2\right)}^3}$ (17)

As the result of integration, we obtain:

$A=-\frac{\pi r_0^3}{4{\left(a+r_0/2\right)}^3}\frac{q^2}{4\pi {\epsilon }_{0}R}-\frac{\pi r_0^3}{16{\left(a+r_0/2\right)}^3}\frac{eq}{4\pi {\epsilon }_{0}R}+\frac{{\pi }^3{a}^3}{32000}\frac{q^2}{4\pi {\epsilon }_0{R}^4}$ (18)

It follows from (16) that the energy spent on vacuum polarization increase as the radius of a moving charged particle decreases. Consequently, the penetrating ability for α-particles is greater than for that of protons in accordance with their size and less in accordance with the increase in charge. In the case of the electrons moving in vacuum, the situation changes drastically. An electron colliding with a quanton is simply captured by it. A new quanton is formed, while the electron of the quanton absorbs the energy released in this process and begins to move in the direction of the original electron with virtually the same energy. That is why the penetrating ability of β-particles far exceeds the penetrating ability of α-particles. When an electron moves in vacuum, the share of lost energy based on (18) amounts to:

$\frac{A}{e^2/4\pi {\epsilon }_0{a}^2}=0.3015-0.0754+0.0035=0.2296$ (19)

This is the energy that was substituted by electron neutrino.

Thus, a free electron, colliding with a collapsed electron-positron pair of physical vacuum in the form of a quanton, is captured by a positron with the formation of a new quanton while the electron of the initial quanton leaves its state in the direction of motion of the trapped electron. Figure 1.3a shows this situation. If the original electron moved in a straight line, then the additional forces did not act on it and therefore the electron that left the quanton, in accordance with the law of conservation of energy, would also move in a straight line.

If a rotating electron is under the action of the force of the positive charge of the nucleus of an atom (molecule), creating centrally symmetric field, then, during the exchange of the quanton with the electron it becomes polarized and a pair of forces begins to act onto it; under this action the quanton begins to rotate (Figure 3). Because of the polarization it presents the source of dipole electromagnetic radiation. In the process of polarization of a quanton, it should be considered as a kind of waveguide in which electromagnetic waves with the critical frequency appear. This is a near-field zone. For this reason, a number of authors pro posed to consider quantum mechanics as unitary theory.³ 

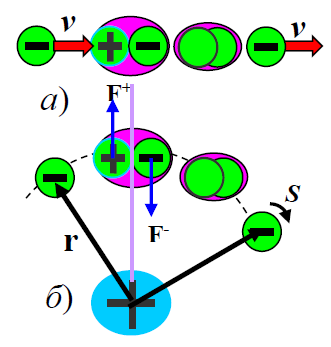
Figure 3 Interaction of electron with quanton: a) – with free one, and b) – with bound one in centrally symmetric field.

E- and H-waves are realized in the near zone. H- wave propagates with phase velocity while E-wave propagates with group velocity. Since only the critical frequency is excited inside the quantum, the group velocity, which transfers energy, is equal to zero, while the phase velocity tends to infinity, and practically transfers no energy. E-wave propagates perpendicular to the line along which the quanton is polarized, and the magnetic wave propagates along the line of oscillation of charges inside the quanton. Particular estimates of the energy transfer of magnetic dipole radiation and electric dipole radiation, reported in,¹ showed that magnetic dipole radiation is a million times smaller than the electric dipole radiation. Similar estimates were reported in.⁴ Therefore, the energy transfer of the polarization of the quanton practically does not occur, and the magnetic dipole radiation, propagating along the direction of the electron movement, lines up the quantons in the direction of free electron motion. Since no radiation occurs into open space, E-wave forms standing wave along the propagation of H-wave. That's actually de Broglie wave.

After the external electron has been captured of by a quanton within the field of central forces, its rotational energy, in accordance with the law of energy conservation, is transferred to the outgoing electron. As a result, all electrons that are located on the internal stationary orbits, rotating around the nucleus of the atom, acquire rotational energy around their own axes, that is, electron spin motion occurs. The frequency and the rotational energy are determined as follows.

Under the action of the external electric field, an electron-positron pair arises as a particle with real mass. In this case, inside the quanton, the electron and the positron will separate from each other by a distance $dr=2.06\cdot {10}^{-17}$ m [1]. On complete separation of the electron and the positron, a new particle-positronium-appears. The distance between the electron and positron in the positronium amounts to m.¹ The time it takes for the full polarization of the quanton accompanied by the occurrence of positronium is as follows:

$N_{k\theta }=\frac{4\pi r^{2}dr}{8{\left(a+r_0/2\right)}^3}$ (20)

where r is the radius of the orbit of the electron's rotation in the atom.

During this time, before the transformation of a quanton into a positronium, a pair of forces acts, leading to the rotation of the quanton. The rotational energy of the quantum is the product of the average value of the dipole electric moment of the quantum and the electric field strength generated by the charge of the nucleus of the atom:

$d{E}_{rot}=\frac{p_e}{2}{E}_e=\frac{ed}{2}\frac{e}{4\pi {\epsilon }_0{r}^2}$ (21)

At the moment when positronium is formed with further transformation into a quanton, the received rotational energy is completely transferred to the electron, which leaves the quanton. The frequency of rotation of the electron around its own axis in the hydrogen atom will amount to:

$S=\frac{1}{2\pi }{\left(\frac{e^2}{4\pi {\epsilon }_0{J}_e{r}^2}\right)}^{1/2}=1.6\cdot {10}^{18}Hz$ (22)

Where is the moment of inertia of rotating electron as a solid particle while r= 0.529•10^-10 m – is the radius of hydrogen atom.

Rotational energy E_rot=9.095·10^-4 eV. This energy is the polarization energy of the quanton of physical vacuum accompanied with the formation of an electron-positron pair and represents a fundamental constant value. Such an energy value as compared with the ionization energy of hydrogen atom can be neglected. A similar situation is realized for other atoms and molecules. The frequency of spin rotation of an electron in each atom in all energy states is constant. This follows from the definition of the frequency of frequency of electron which is equal to:

$f=\frac{\omega }{2\pi }=1.6\cdot {10}^{18}1/s$ (23)

This frequency, along with rotational energy represents a fundamental physical quantity; it is equal to:

Thus, the speed the electron moves along a given orbit is of no importance; its rotational energy is determined only by the work spent on charge separation in a quanton when it decays into real mass particles: an electron and a positron. Therefore, the constancy of the rotation energy of electron stems from the properties of the physical vacuum but not by the energy bond with the nucleus of an atom.

Hence, carried out investigations yielded the following results:

1. The representation of electric charge in the complex domain means a notably significant event in electrodynamics, since Dirac monopole is now properly interpreted, electric and magnetic charges are interrelated, Lorentz equation determines the interaction of complex charges, and the product of the electric charge by its speed presents the manifestation of an imaginary magnetic charge in real space and imaginary time. Correct definition of quanton as the sum of elementary charges, presented in complex form has been given.
2. The structure of the physical vacuum has been determined, consisting of non- interacting neutral quantons featuring electrical and magnetic moments randomly distributed in space. External influences of electric, magnetic and electromagnetic fields lead to the deformation of quantons while the deformed state itself is the carrier of the energy of the acting fields. The energy is contained not in the charge, nor in the field, but in the deformed state of the physical vacuum.
3. The interaction of charged particles with the physical vacuum has been considered and the following has been determined:
1. Substantial perturbation of the physical vacuum occurs by particles with smaller geometric sizes and larger electric charges.
2. Electrons move in the physical vacuum by successive capturing an electron by the quanton and the release of the bound electron with the transfer of total energy of the original electron.
3. When an electron moves in centrally symmetric field of an atom or a molecule, its spin energy and rotation frequency present fundamental constants and is determined by the properties of the physical vacuum. For the first time, theoretical calculations of the energy and the rotation frequency of electron spin have been performed.

None.

Author declares that there is no conflict of interest.

1. Gretchikhin LI. Radio Basics. Minsk: National library of Belarus; 2016. 377 p.
2. Sommerfeld A. Electrodynamics. New York: Pergamon Press; 1952. 347 p.
3. Sapogin LG, Ryabov Yu A, Uchastkin VI. Unitary quantum theory and new energy sources. MADI (SU); 2003. 174 p.
4. Elyashevich MA. Atomic and Molecular Spectroscopy. Minsk: FM; 1962. 892 p.