The main aim of this paper is to present of hydrazine monopropellant catalyst bed optimization methodology. To this end, the main parameters of hydrazine catalyst bed in optimization are decomposition products properties, molecular weight, specific heat ratio and their temperature as function of hydrazine decomposition and ammonia dissociation. These parameters are function of catalyst type, size, and geometry, reaction chamber pressure, and propellant dwell time. Also the objective functions in the optimization are catalyst bed’s weight and performance. First one, a parametric study on hydrazine decomposition products as a function of catalyst bed design has been done. Catalyst bed output temperature, specific heat ratio and molecular weight were calculated as hydrazine and Ammonia dissociation ratio. Thermo chemical result shows that best specific velocity is attained when %25 of ammonia is allowed to dissociate. Pellet diameter, bed loading factor and thrust chamber pressure are assumed as the preliminary design parameters of the catalyst bed to find the catalyst bed length and pressure drop. Finally a numerical simulations, one dimensional, steady state, adiabatic, homogeneous, creeping and uniform flow at axial sections or Plug flow that has chemical reaction across a constant cross-sections catalytic bed, for different pellet diameters, loading factor and chamber pressure, have been carried out with the help of a validated formulations. According to this study, catalyst bed length and pressure drop will increase as the pellet diameter or bed loading increases. However the increase of chamber pressure will lead to the lessening catalyst bed length and pressure drop, but this influence is ignorable.

Keywords: Monopropellant, thruster, hydrazine, parametric study, modeling

The attractiveness of monopropellant thrusters is based on its operational and structural simplicity. Monopropellant thrusters are usually used to attitude and orbit control of spacecraft. These thrusters use catalytic decomposition to change the propellants chemical energy to thermal energy.¹ Although Hydrazine,² hydrogen peroxide,^3,4 Hydroxyl Ammonium Nitrate (HAN),⁵ De-Methyl Amino Ethyl Aside, hydrazinium nitro formate (HNF) and Nitro oxide⁶ are proposed as liquid monopropellant; hydrazine has received a great deal of attention for many years for space applications that require very high reliability. Monopropellant thruster is composed of thruster valve, injector, catalyst bed, nozzle and body. Except the catalyst bed the other ones are the same mono and bipropellant motor, so it’s the most important element of a monopropellant thruster system. In the other hand as the catalyst bed controls propellant decomposition, which determines the overall thruster performance, the importance of this item heightens. Transition metal and their derivatives have excellent catalytic behavior. Between these, the traditional hydrazine catalyst is a 20–40 wt% Ir/g-Al₂O₃ catalyst. The most successful hydrazine decomposition catalyst to date until 1963 is Shell 405. Shell 405 is 32% iridium over support of alumina, which is capable of surviving several hundred cold starts with no significant degradation. As iridium is a rare and noble metal the Ir-based catalyst is very expensive and many effort have been done to achieve an inexpensive, active, stable and readily available catalyst for hydrazine decomposition. In this paper an idealized design of a hydrazine monopropellant catalyst bed is carried out for the aerospace applications.

In this study, the approach of using Kriging meta-model methodology in the multi-objective Gray Wolf Optimization problems is developed. The MOGWO based on Kriging meta-model methodology is shown in Figure 1.

Figure 1 Kriging Meta-model methodology algorithm.

Meta-model creation

The exact model applied in the multi-objective optimization can lead to high time-consuming processes. Hence, using surrogate modelling in the optimization process will reduce the calculation effort. Thus, Kriging meta-model is used in for developing the surrogate model. The procedure is arranged as following steps.

1. The DOE is built by Inheritable Latin Hypercube Design (ILHD).
2. Based on the design parameters in each experiment, an exact analysis is performed and the system responses are developed.
3. About 20% of the samples are randomly selected as test points and used as inputs for surrogate modeling.
4. The surrogate model is generated based on Kriging meta-model.
5. The response of the system is predicted base on meta-model to test data.
6. Root Mean Squared Error (RMSE) is calculated by comparing the meta-model with exact outputs.
7. For the RMSE less than 98%, a new design experiments is built by increasing the number of populations up to 50%. This procedure will be continued until the condition of meta-model creation satisfied.
8. A sensitivity analysis is performed by the final responses of the DOE.

Multi-objective gray wolf optimization

Multi-objective optimization problem is generally defined as follows:

$\begin{array}{l}MinimizeF\left(x\right)={\left[F_1\left(x\right),F_2\left(x\right),\dots ,F_k\left(x\right)\right]}^T\\ Subject\{\begin{array}{c} g_j\left(x\right)\le 0 ; j=1,2,\dots ,m\\ h_i\left(x\right)=0 ; i=1,2,\dots ,e\end{array}\end{array}$ (1)

Herein, Gray Wolves Optimization (GWO) is used as the optimizer. This method is an ultra-fast optimizer with fast convergence and the ability to avoid interception in local optimizations. This algorithm has been implemented with inspiration from the hierarchical leadership and the hunting method of gray wolves. Archiving the non-dominated Pareto optimal solutions assisted by a leader selection strategy is the method to perform multi-objective optimization by GWO.

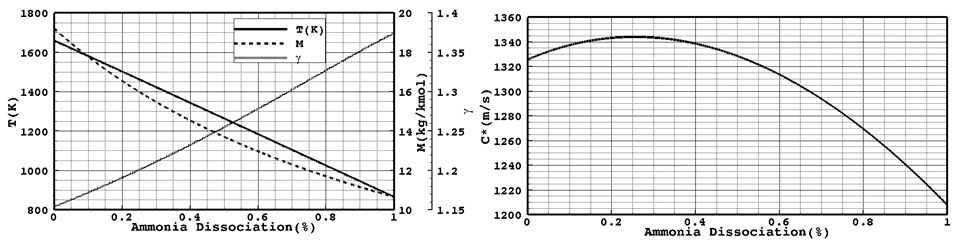
Hydrazine propellant decomposes to nitrogen and ammonia in vicinity of its catalyst according to Eq1. Hydrazine decomposition is a volume expansion and exothermic reaction. As a result, the chamber pressure and temperature rises rapidly. The released energy of this reaction is about 336.3kjol/mol.⁷Additionally, ammonia usually dissociate to nitrogen and hydrogen at elevated temperatures According to Eq. 2. Ammonia decomposition is an endothermic reaction and its absorption energy is about 144.5kjol/mol. So the hydrazine decomposition in a reaction chamber can be simplified as Eq2. where Y is ammonia dissociation ratio.

${\text{3N}}_{\text{2}}{\text{H}}_{\text{4}}\stackrel{\text{Cat}}{\to }\text{ 4(1-}\psi {\text{)NH}}_{\text{3}}\text{+(1}+\text{2}\psi {\text{)N}}_{\text{2}}\text{+6}\psi {\text{H}}_{\text{2}}$ (2)

As a result the hydrazine decomposition products properties, molecular weight, specific heat ratio, temperature and their specific velocity, as shown in Figure 2 depend on hydrazine decomposition and ammonia dissociation proceeding. The best specific velocity and specific impulse is attained when little ammonia, about %20, is allowed to dissociate. In a catalyst bed with a porosity ε composed of catalytic particles with an equivalent diameter d_p, the mass ratios of the reactants y_i across the bed can be calculated from Eq. 3 through 6.

$\frac{{\text{dy}}_{{\text{N}}_2{\text{H}}_4}}{\text{dx}}=\frac{1}{\text{G}}\{-\text{ε}{\dot{r}}_{{\text{N}}_2{\text{H}}_4}^{\text{hem }}–{\text{A}}_{\text{P}}{\left({\text{K}}_{\text{C}}\text{C}\right)}_{{\text{N}}_2{\text{H}}_4}-{\stackrel{.}{m}\left(\frac{\text{C}}{\text{ρ}}\right)}_{{\text{N}}_2{\text{H}}_4}\}$ (3)

$\frac{{\text{dy}}_{{\text{N}}_2{\text{H}}_4}}{\text{dx}}=\frac{1}{G}\{\frac{y_{N{H}_3}}{y_{N_2{H}_4}}(\text{ε}{\dot{r}}_{{\text{N}}_2{\text{H}}_4}^{\text{hem }}–{\text{A}}_{\text{P}}{\left({\text{K}}_{\text{C}}\text{C}\right)}_{{\text{N}}_2{\text{H}}_4})-{\text{A}}_{\text{P}}{\left({\text{K}}_{\text{C}}(C-{C_p}_{{}_s})\right)}_{N{H}_3}-\stackrel{.}{m}{\left(\frac{\text{C}}{\text{ρ}}\right)}_{N{H}_3}\}$ (4)

$\frac{{\text{dy}}_{{\text{N}}_2}}{\text{dx}}=\frac{1}{G}\{\frac{1}{2}(\frac{y_{N_2}}{y_{N_2{H}_4}}(\text{ε}{\dot{r}}_{{\text{N}}_2{\text{H}}_4}^{\text{hem }}–{\text{A}}_{\text{P}}{\left({\text{K}}_{\text{C}}\text{C}\right)}_{{\text{N}}_2{\text{H}}_4})-\frac{y_{N_2}}{y_{N_2{H}_4}}{\text{A}}_{\text{P}}{\left({\text{K}}_{\text{C}}(C-{C_p}_{{}_s})\right)}_{N{H}_3})-{\stackrel{.}{m}\left(\frac{\text{C}}{\text{ρ}}\right)}_{N_2}\}$ (5)

$\frac{{\text{dy}}_{{\text{H}}_2}}{\text{dx}}=\frac{1}{G}\{\frac{1}{2}(\frac{y_{H_2}}{y_{N_2{H}_4}}(\text{ε}{\dot{r}}_{{\text{N}}_2{\text{H}}_4}^{\text{hem }}–{\text{A}}_{\text{P}}{\left({\text{K}}_{\text{C}}\text{C}\right)}_{{\text{N}}_2{\text{H}}_4})-3\frac{y_{N_2}}{y_{N{H}_3}}{\text{A}}_{\text{P}}{\left({\text{K}}_{\text{C}}(C-{C_p}_{{}_s})\right)}_{N{H}_3})-\stackrel{.}{m}{\left(\frac{\text{C}}{\text{ρ}}\right)}_{N_2}\}$ (6)

                                                                     A                                                                                                 B

Figure 2 The hydrazine decomposition: A) Products property; B) Products specific velocity changes as a function of Ammonia dissociation.

$\stackrel{.}{m}$ and G are the propellant mass flow rate and propellant loading factor trough the catalyst bed, respectively.${\text{A}}_{\text{P}}=\frac{\left(1-\text{ε}\right)}{12{\text{d}}_{\text{P}}}$ is the catalyst bed specific aria per unit volume, which can be calculated from Eq. Error! Reference source not found.${\text{K}}_{{\text{C}}_{\text{i}}}$ is the mass transfer coefficient and defined as follows.

${\text{K}}_{{\text{C}}_{\text{i}}}=\frac{0.185928\text{G}}{\text{ρ}}{\text{Sc}}^{0.667}{\text{Re}}^{-0.41}$ (7)

The sepsis e concentration changes can be calculated from Eq. 8.

$\frac{d{C}_i}{dx}=\rho \frac{d{Y}_i}{dx}+\frac{C_i}{\rho }\frac{d\rho }{dx}$ (8)

where $\text{ρ}$ is the mixture density. The variation in the mixture density with the assumption of complete gas can be calculated from Eq. 9.

$\frac{d\rho }{dx}=\rho \left[\frac{1}{P}\frac{dP}{dx}+\frac{1}{\overline{M}}\frac{d\overline{M}}{dx}-\frac{1}{T}\frac{dT}{dx}\right]$ (9)

$\overline{M}$ is the mixture equivalent molar mass and can be calculated from Eq. 10.

$\frac{d\overline{m}}{\text{dx}}=\frac{{\displaystyle {\sum }_{\text{i}=1}^{\text{n}}\frac{1}{{\text{M}}_{\text{i}}}\frac{{\text{dy}}_{\text{i}}}{\text{dx}}}}{{\displaystyle {\sum }_{\text{i}=1}^{\text{n}}\frac{{\text{y}}_{\text{i}}}{{\text{M}}_{\text{i}}}}}$ (10)

Assuming a adiabatic process, the reaction temperature changes can be calculated as the ratio of the enthalpy variations to the mixture specific heat, as presented in Eq.11.

$\frac{\text{dT}}{\text{dt}}=\frac{{\displaystyle {\sum }_{\text{i}=1}^{\text{n}}-{\stackrel{.}{r}}_{\text{i}}{\text{ h}}_{\text{i}}}}{{\displaystyle {\sum }_{\text{i}=1}^{\text{n}}-{\text{C}}_{\text{i}}{\text{C}}_{{\text{P}}_{\text{i}}}}}$ (11)

A modified Ergun Equation was used to calculate the catalyst bed pressure drop.

$\frac{\text{dP}}{\text{dx}}=\frac{4\text{G}}{{\text{d}}_{\text{P}}{}^2{\text{ρε}}^3}\left(45\text{μ }{\left(1-\text{ε}\right)}^2+{\text{d}}_{\text{P}}\text{G}\left(1-\text{ε}\right)\right)$ (12)

Changes in the concentration of ammonia and temperature at each point of the catalyst porous particles can be calculated from the following approximation.${\text{K}}_{\text{P}}$ is the thermal conductivity of porous catalyst particles.

The Kriging meta-model methodology algorithm in multi-objective gray wolf optimization problem is shown in Figure 1. The aim of this section is to apply the methodology to the design process of space low thruster (with 22 N thrust). An example of the response surface generated by this meta-modeling is presented in Figure 3. The catalyst bed sensitivity analysis results are presented in Table 1 as a design structure matrix. According to the catalyst bed design structure matrix, Table 1, all design parameters are independent of each other. Also, The DSM shows that the responses are In conflict with each other to each other, which confirms the use of the multi-objective optimal design approach. The optimization results of this study are shown as an optimization response called the Pareto front. Pareto front curve or response surface is composed of non-dominated optimization results. Pareto optimal sets allow the designer and decision makers to access a variety of optimal scenarios and choose the one of the best suits the demands of a particular project.⁸ Monopropellant catalyst bed multi-objective optimization Pareto front is shown in Figure 4.

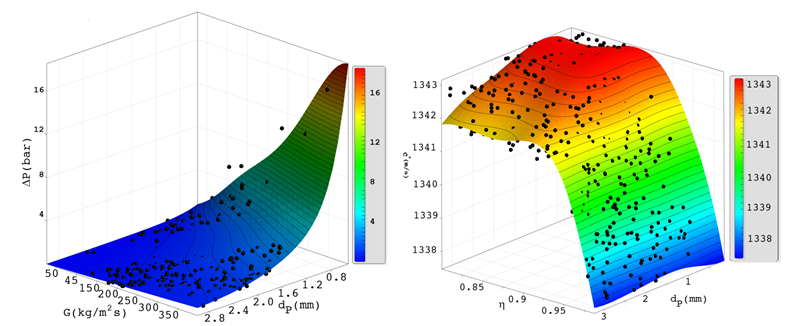
Figure 3 Catalyst bed pressure drop and specific velocity response surface as a function of catalyst bed design parameters.

Figure 4 Pareto front multi-objective optimization for monopropellant catalyst.

A novel multi-objective gray wolf optimization assisted by Kriging meta-model is provided in this study. This systematic approach is lead to an accurate, efficient and fast converging multi-objective optimization. The catalyst bed of a hydrazine space low thruster was considered as case study. Three objectives, increasing catalyst bed efficiency and reducing its mass and pressure drop, are considered as the catalyst bed optimization criteria. The proposed approach can be utilized in other engineering optimization problems.

None.

Authors declare that there is no conflict of interest.

1. Sutton GP, Biblarz O. Rocket propulsion elements. New York: John Wiley & Sons; 2010. 784 p.
2. Adami A, Mortazavi M, Nosratollahi M, et al. Multidisciplinary Design Optimization and Analysis of Hydrazine Monopropellant Propulsion System. International Journal of Aerospace Engineering. 2015;295636:1‒9.
3. Rhee MS, Thomas MA. Highlights of Nanosatellite Propulsion Development Program at NASA. Goddard Space Flight Center. Logan, UT: 14th Annual AIAA/USU Conference on Small Satellites; 2000.
4. Whitehead JC. Hydrogen Peroxide Propulsion for Smaller Satellites. Logan: 12th Annual AIAA/USU Conference on Small Satellites; 1998.
5. Chen J, Li G, Zhang T, et al. Experimental investigation of the catalytic decomposition and combustion characteristics of a non-toxic ammonium dinitramide (ADN)-based monopropellant thruster. Acta Astronautica. 2016;129:367‒373.
6. Lohner K, Scherson Y, Lariviere B, et al. Nitrous Oxide Monopropellant Gas Generator Development. 3rd Spacecraft Propulsion Joint Subcommittee Meeting, JANNAF; 2008. 13 p.
7. Makled A, Belal H. Modeling of hydrazine decomposition for monopropellant thrusters. Egypt: 13th International Conference on Aerospace Sciences & Aviation Technology; 2009. 22 p.
8. Mokarram V, Banan MR. A new PSO-based algorithm for multi-objective optimization with continuous and discrete design variables. Structural and Multidisciplinary Optimization. 2018;57(2):509‒533.