Novel aircraft configuration, such as drones, have emerged during the last decades. This project aims to offer insights into drone development, enhancing its efficiency by means of rotor optimization utilizing well-established theoretical models based on blade element momentum theory for estimating thrust generation and power requirements at hover and forward flight. The impact on performance of chord and airfoils pitch angle, particularly focusing on the twist, which is how pitch changes along the blade, is analyzed, followed by optimizations of multiple chord and twist distributions at different flight conditions. Additionally, Computational fluid dynamics tools are employed to simulate resulting rotor geometries and to the baseline. Simulations and model predict power reductions of 3% to 17%, with negative twist rates and increased platform as main characteristics of most efficient geometries.

Keywords: drone, rotor, twist, chord, optimization, CFD

In recent decades, the aviation industry has witnessed remarkable advancements, particularly with the emergence of drones, these new vehicles have rapidly gained prominence due to their versatility. As the demand for drone technology continues to grow, there is an inherent need to overcome technological challenges and drive innovation. The goal of this project is to provide new insights and analyze possible paths of evolution of small rotors, which can contribute to reduce power consumption and enhance performance capabilities such as range or autonomy. Large scale rotors, used in helicopters, have larger efficiencies than small scale rotors as pointed out by R. Cagnato,¹ these inefficiencies are mainly related with the size of the rotors and its implication in their Reynolds flight regime $(Low Reynolds,Re<{5.10}^5)$ ,² which implies bad aerodynamic efficiency. Consequently, it is important to analyze all the parameters related to rotor performance and try to enhance it. Among all the geometrical parameters defining rotor’s geometry, this project focuses on two: twist distribution and platform shape by means of chord distribution.

Improving the efficiency through geometrical optimization has historically been a matter of significant interest. There are multiple studies analyzing all the implications of geometry modification in rotor’s efficiency for large scale rotors. In fact, there are even theoretical optimal configurations with hyperbolic chord and twist distributions for hovering, as noted by Joanne L. Walsh,³ who also showed the benefits of tapered blades and negative twist not only for hovering but also for forward flight regime. However, the number of studies about small scale rotors is not that large. Moreover, the operation at low Reynolds has significant implications in the performance, which may affect to the final optimal geometries implying that general ideas of large scall rotors do not apply to small rotors. At low Reynolds, where viscous effects are dominant, it occurs complex phenomena that leads to low aerodynamic efficiency. Separation of the flow followed by reattachment leading to the formation of large separation bubbles, which are linked to poor lift/drag ratio. Those problems were pointed out by F. Bohorquez,⁴ who analyzed the effect of several geometrical parameters for rotors operating at $(Re\sim {6.10}^4)$ . Bohorquez provides interesting conclusions about chord and twist, by performing test and creating hybrid models between theoretical approaches and computational fluid dynamics (CFD). He pointed out the benefits obtained by larger chords platforms opposite to optimal large-scale rotors, for which low chord produces low solidity being it beneficial. Bigger chords enhance aerodynamic efficiency, it implies larger Reynolds regime and lower thickness ratio of airfoils, which enhances performance at low Reynolds. Moreover, he remarked improvements due to negative twist and benefits of taper near the tip of the blade. Additionally, other researchers such as J. Winslow et al.,⁵ studied the performance of these rotors. Among its conclusions, they remark the differences with large scale rotors due to a bigger impact of profile loses, which diminishes the effectiveness of twist and chord modifications that aimed to reduce inflow loses by creating a more uniform distribution. Despite the improvement was not as large as it can be for larger scale rotors, they concluded that negative twist is necessary for enhancing aerodynamic performance. Moreover, like Bohorquez, They conclude that larger chords enhanced the performance and taper blades showed negligible benefits except for large reductions near the tips. Other scholars like J. Wiebe⁶ performed optimizations using theoretical models, characterizing the airfoils properties with simpler tools such as XFOIL software. He remarked the limitations of theoretical models. Moreover, he approached the optimization using MATLAB toolbox and implementing interesting distributions defined by spline curves for both chord and twist. However, the performance of small-scale rotos is not only carried out by theoretical models but in fact, for a proper comprehension more complex tools are required like: CFD or even experimental test. Kodchaniphaphong et al.,⁸ carried out CFD simulations that were compared against experimental test of small-scale rotors in both regimes: hovering and forward flight, showing good predictions. R. Cagnato and C. Vasconcelos,^1,7 also used CFD for characterizing and analyzing more complex phenomena of the rotor’s performance, using different approaches for the same type of simulations, Multiple reference frame (MRF) and Sliding mesh.

Supported by the ideas of the current state of the art, this project pursuits the estimation of rotor performance and possible chord and twist distributions for improving it in hover and forward flight using MATLAB version R2022b,⁹ blade element momentum theory (BEMT) and airfoils properties estimated by software for preliminary designs tasks like XFOIL 6.99.¹⁰ Concluding with CFD simulations with Fluent by Ansys version 2021 R2.¹¹

Next section contains the theoretical background required for the models as well as the assumptions and hypothesis assumed.

Low Reynolds regime and aerodynamic properties

As emphasized, the rotors of drones operate in a different Reynolds regime compared to large-scale rotors. This has implications for the model, not only because the aerodynamic efficiency is severely affected, as noted in,⁴ but also because it affects the typical assumptions made in blade theory.

At high Reynolds regimes, lift (Cl) and drag coefficients (Cd) barely depend on Reynolds number. Moreover, the behaviour with the angle of attack (AoA) is approximately linear for lift and quadratic for drag. However, due to the greater impact of viscosity and the presence of phenomena such as large separation bubbles (LSB), these assumptions cannot be kept at low Reynolds. Multiple studies have analyzed this regime and the performance of airfoils under these conditions,¹² trying to understand the behaviour of airfoils.

It is crucial to estimate the aerodynamic properties of the airfoils (NACA 0012) (lift and drag coefficients, Cl, Cd) for the rotor models. As stated in¹⁴ XFOIL is an interesting tool due to its simplicity, time cost and fairly good results. Figure 1 shows a comparative against experimental data.

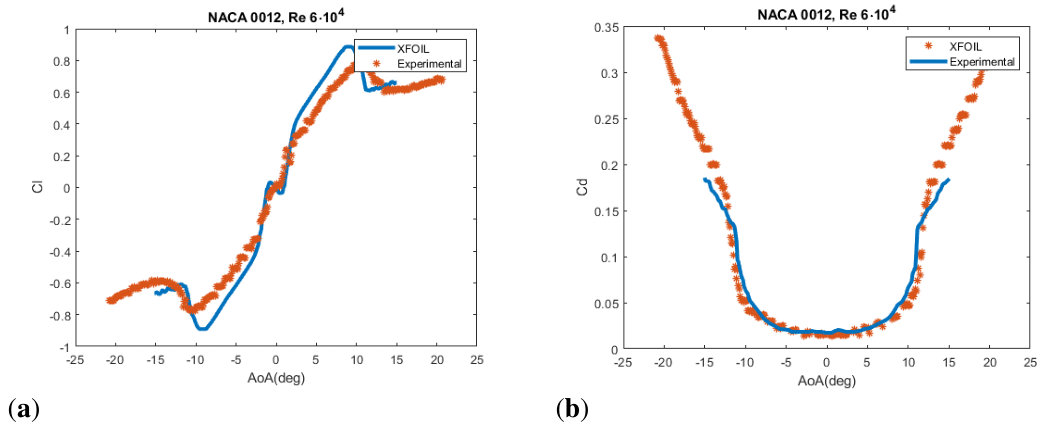
Figure 1 Comparison between XFOIL NACA 0012 data and experimental data from¹³ for $Re=6\cdot {10}^4$
(a) Lift coefficient (Cl) versus angle of attack (AoA) (b) Drag coefficient (Cd) versus AoA.

XFOIL, which uses theoretical transition approach, is useful for low Reynolds computations as demonstrated by its developer M. Drela in.¹⁵ In terms of error, as pointed out in,⁶ it is optimistic predicting lift coefficient and stall point. Bohorquez³ discouraged using traditional thick airfoils for small rotors. However, blade airfoil section effect is not the goal of the project. NACA 0012 was chosen because it is one of the most studied airfoils, the amount of data available at low Reynolds was bigger and if required, fabrication would be easier due to its symmetry.

Theoretical background

Rotors performance models are based on Blade Element Momentum Theory (BEMT) adapted at each flight regime. This theory is a combination of two others: Momentum theory and Blade Element Theory (BET).

Momentum theory

Momentum theory assumes that a stream-tube, Figure 2, appears in the rotor vicinity. This 1-D theory uses conservation laws of: mass, momentum, and energy in the control volumes, above and below the rotor disk. All the hypothesis required for this theory are found in the book written by Leishmann.¹⁶

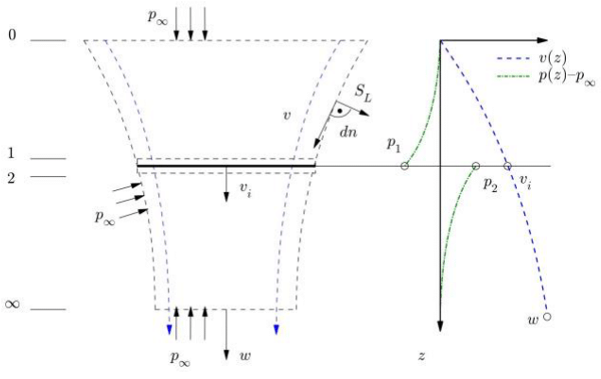
Figure 2 Scheme of the stream-tube with control volume definitions and lateral pressure distribution for Von Misses hypothesis.

After performing the mass, momentum and energy balances, it is obtained the next relationships with relate the thrust (T), induced power$(P_i)$ and induced speed $(v_i)$ with: the mass flow (m), the rotor area $(A_R)$ , defined with the rotor radius (R), the pressures above and below the rotor $\left(p_1, p_2\right)$ , the density $\left(\rho \right)$ and the entrance and exit speeds $\left(v_0, w\right)$ .

$\begin{array}{l}\dot{m}=\rho A_r{v}_i=\rho A_1{v}_0=\rho A_{\infty }w\\ T=\left(p_2-p_1\right)A_R=\dot{m}w\\ T{v}_i=\frac{1}{2}\dot{m}{w}^2\\ m=2v_i\end{array}$ (1)

This approach was adapted for forward flight by Glauert.¹⁶ Again, assuming the stream-tube, Figure 3. Two control volumes are defined, and the balances are computed in the normal direction to the disk area of the rotor. This theory works for medium and high advance speeds. Full explanation can be found in detail.¹⁶

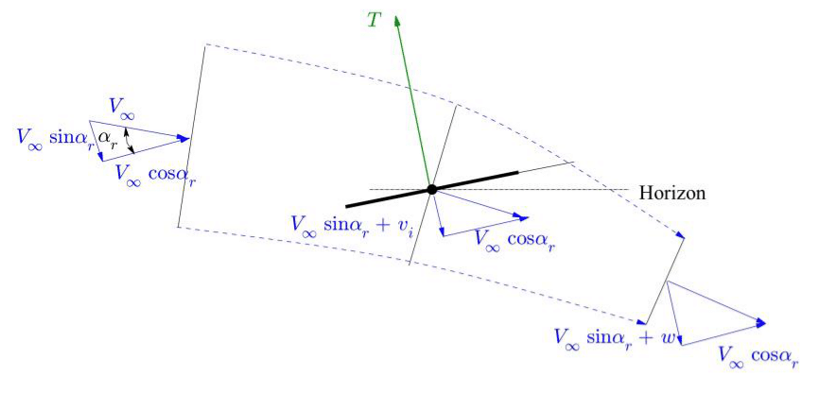
Figure 3 Stream-tube scheme for forward flight.

New terms appear in the equations from the balances: the rotor inclination angle $\left({\alpha }_r\right)$ and the advance speed of the vehicle $\left(V_{\infty }\right)$ .

$\begin{array}{l}V=\sqrt{{\left(V_{\infty }sin{\alpha }_r+v_i\right)}^2+{\left(V_{\infty }cos{\alpha }_r\right)}^2}\\ T=m\left(V_{\infty }sin{\alpha }_r +\dot{w}\right)-\dot{m}{V}_{\infty }sin{\alpha }_r\\ T\left(V_{\infty }sin{\alpha }_r+v_i\right)=\frac{1}{2}\dot{m}\left(V^2-V_{\infty }^2\right)\\ w=2v_i\end{array}$ (2)

Blade element theory (BET)

Momentum theory does not consider any aspect related with rotor geometry except for the radius. The estimations are based on conservation laws and not on aerodynamic principles neglecting viscosity, hence drag forces and parasite power cannot be computed. BET computes rotors forces, torque (Q) and power, induced and parasite $\left(P_i, P_0\right)$ , based on 2-D theory using the aerodynamic forces at each blade section and integrating along the blade. Only some 3-D effects can be implemented by modifications of the theory.

Figure 4, shows the velocities over the blade section, radial $\left(U_R\right)$ , which is neglected, tangential $\left(U_T\right)$ and perpendicular $\left(U_P\right)$ as well as the differential forces $\left(d{F}_z,d{F}_x\right)$ and the aerodynamic terms lift, drag and moment (L,D,M). Additionally, it appears the geometrical pitch $\left(\theta \right)$, the angle of attack $\left(\alpha \right)$ and the inflow angle $\left(\varphi \right)$ as well as the non-dimensional radius $\left(r=y/R\right)$ . By composition of those forces, the expressions that integrated along the blade provide the final computation are reached.

$U_P=v_i, U_T=\text{Ωr}R, \alpha =\theta -\varphi \to \varphi =\text{atan}\left(\frac{U_P}{U_T}\right)$ (3)

Lift and drag are computed using the dynamic pressure $\left(1/2\rho U^2\right)$ , the chord distribution (c) and the airfoil properties: lift and drag coefficient (Cl,Cd).

$\begin{array}{l}dL=\frac{1}{2}\rho U^{2}Clcdy,dD=\frac{1}{2}\rho U^{2}Ccdy\\ d{F}_z=dLcos\varphi -dDsin\varphi , d{F}_x=dLsin\varphi +dDcos\varphi \end{array}$ (4)

Finally, differential expressions of thrust, torque and power are obtained using the number of blades (b) and the rotational speed (Ω).

$dT=bd{F}_z, dQ=bd{F}_{x}rR, dP=bd{F}_x\text{Ω}rR$ (5)

Frequently, these final expressions are non-diomensionalized using the rotor area $\left(A_r\right)$ , the tip speed $\left(\text{ΩR}\right)$ and new parameters, the solidity $\left(\sigma =\left(bc\right)/\left(\pi R\right)\right)$ and the inflow parameter $\left({\text{λ=U}}_{\text{P}}\text{/}\left(\text{ΩR}\right)\right)$ .

$\begin{array}{l}d{C}_T=\frac{dT}{2\rho A_r{\left(\text{Ω}R\right)}^2 }=\frac{1}{2}\sigma \left(Cl\cos f-Cd\sin f\right)\left(r^2+{\lambda }^2\right)dr\\ d{C}_P=\frac{dP}{2\rho A_r{\left(\text{Ω}R\right)}^3 }=\frac{1}{2}\sigma \left(Cl\sin f+Cd\cos f\right)\left(r^2+{\lambda }^2\right)rdr{\rm A}\end{array}$ (6)

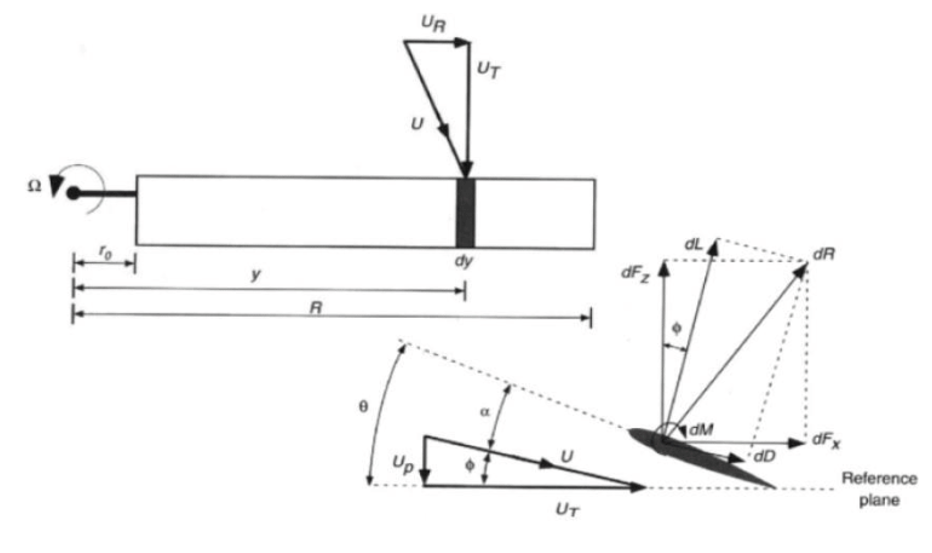
Figure 4 Blade Element theory model, forces, and velocities at the blade section.¹⁶

Similarly to momentum theory, BET can be applied in forward flight. The main difference is the velocity field and the forces, Figure 5. At forward flight, velocity field is not axisymmetric, the magnitudes must be averaged in a revolution because they depend on the azimuth position (ψ).

Whereas the expressions of lift and drag forces do not change from equation 4, tangential and perpendicular speeds do, as well as the final forces. Moreover, the axial force $\left(F_x\right)$ of the previous scheme, which is denominated as dragging force, is split in two (Y,H). Apart from that, functions $\left(F_t, F_h\right)$ are implemented for quantifying losses at the tip and hub, more information about them is available in.¹⁶

$\begin{array}{l}{U}_P=V_{\infty }sin{\alpha }_r+v_i, U_T=\Omega r+V_{\infty }cos{\alpha }_{r}sin\psi \\ dCT=\frac{1}{2}\sigma \left(Clcos\varphi -Cdsin\varphi \right)U^2{F}_t{F}_{h}dr\\ dCQ=dCP=\frac{1}{2}\sigma \left(Clsin\varphi +Cdcos\varphi \right)U^{2}rdr\\ dCY=\frac{1}{2}\sigma \left(Clsin\varphi +Cdcos\varphi \right)U^2\cos \psi dr\\ dCH=\frac{1}{2}\sigma \left(Clsin\varphi +Cdcos\varphi \right)U^{2}sin\psi dr\end{array}$ (7)

Frequently, the theory is simplified assuming small angles, tangential speed much bigger than perpendicular speed and high Reynolds simplifications $\left(Cl\approx C{L}_{\alpha }\alpha , Cl\ll Cd\right)$ , which should not be applied for small scale rotors.

Figure 5 Blade Element theory scheme for forward flight, forces, and velocities at the blade section.

Blade element and momentum theory 

As subjected, BET considers geometrical blade parameters for computing the total power of the rotor. However, the induced speed or the inflow (λ) required for the computation must be provided whereas the momentum theory estimates it using the thrust. The momentum theory applied in differential form,¹⁶ (annular sections), combined with BET creates the final approach used for the computations, the blade element and momentum theory (BEMT), using the equality of the expressions of thrust coefficient (CT) provided by BET and differential momentum theory.

$\begin{array}{l}dCT=\frac{\sigma }{2}C{l}_{\alpha }\left(\theta -\frac{\lambda }{r}\right)r^{2}dr=4{\lambda }^2{F}_t{F}_{h}rdr\\ \lambda =-\frac{\sigma C{l}_{\alpha }}{16}+\sqrt{\frac{\sigma C{l}_{\alpha }}{16}+\frac{\sigma C{l}_{\alpha }\theta r}{8F_t{F}_h}}\end{array}$ (8)

Previous expression is obtained assuming the simplified form of BET and the differential momentum theory. Moreover, it takes into the account tip and hub 3-D losses with the functions $\left(F_t, F_h\right)$ , proposed by Prandtl and Lieshmann. More details about the functions can be found in.¹⁶ Besides that, the inflow can be expressed with the full BET, without linearization, as it is done in.⁶ However, during the validation, it was observed that for low Reynolds were drag can be high and NACA 0012 can generate even negative lift with positive angles, Figure 1, imaginary terms would appear making impossible to converge the solutions. To solvent that issue and still consider the non-linearity and the dependence with the Reynolds number, lift curves were approached with linear segments, Figure 6.

Equation 5 is applied modifying the pitch angle using the database with the slopes and the initial angles of each segment $\left(C{l}_{\alpha }, C{l}_0\right)$ depending on the Reynolds at each section.

$dCT=\frac{\sigma }{2}C{l}_{\alpha }\left(\alpha +\frac{C{l}_o}{C{l}_{\alpha }}\right)dr=\frac{\sigma }{2}C{l}_{\alpha }\left(\theta -\frac{\lambda }{r}+\frac{C{l}_0}{C{l}_{\alpha }}\right)r^{2}dr\to {\theta }^{\prime }=\theta +C{l}_0/C{l}_{\alpha }$ (9)

Additionally, because of the tip and hub losses, the equation 5 is coupled. Hence, the problem must be solved using an iterative procedure as it is described in.¹ Apart from that, the model can compute the required pilot input to provide a specific thrust or just to compute the thrust generated for a fixed configuration. The pilot input is typically the collective pitch but it was also considered the rotational speed (Ω), which is used for drones. The computation is performed using a numerical solution by Newton-Raphson with MATLAB fsolve function.

Glauert related the inflow at forward flight and hover¹⁶ so it was obtained an average inflow $\left({\lambda }_0\right)$ from a biquadratic equation. Using the advance parameters $\left({\mu }_x,{\mu }_y\right)$ and the thrust coefficient (CT) and the induces inflow

$\left({\lambda }_i=v_i/\left(\text{Ω}R\right)\right)$ .

$\begin{array}{l}{\mu }_x=\frac{V_{\infty }cos{\alpha }_r}{\text{ΩR}}, {\mu }_z=\frac{V_{\infty }sin{\alpha }_r}{\text{Ω}R}, {\lambda }_0={\mu }_z+{\lambda }_i\\ {\lambda }_i=\frac{CT}{2\sqrt{{\mu }_x^2+{\lambda }_0^2}}\end{array}$ (10)

For large scale rotors, if $({\mu }_x>0.1)$ , it is observed some linear behavior in the inflow distribution. In¹⁶ linear models are gathered. Among all, it was adopted the Pitt & Petters approach, which uses the skew wake angle $(\chi =\text{atan}\left({\mu }_x/\left({\mu }_z+{\lambda }_i\right)\right)$

$\lambda ={\lambda }_0\left(1+k_{x}cos\psi +kysin\psi \right)\to k_x=\frac{15\pi }{23}\tan \left(\frac{\chi }{2}\right), k_y=0$ (11)

Figure 6 Lift coefficient curve and linear approximation (a) Cl versus α for $Re={10}^5$ ; (b) Cl versus for $Re=1.8\cdot {10}^5$ .

However, contrary to hover condition, in which the force balance is just compensating the weight and the thrust coefficient is easily estimated, at forward flight the force balance gains complexity. Moreover, the inclination angle of the rotor is unknown. Since the force balance is not determined due to the number of initial unknowns and equations, it would be needed an iterative process for determining initial value of (H) or to provide some inputs for reducing the number of unknowns. The drone inclination angle $\left({\alpha }_r\right)$ , the velocity $\left(V_{\infty }\right)$ and the flight trajectory $\left(horizontal {\gamma }_h=0\right)$ are inputs as well as the weight of the vehicle (W). The inclination is related to the advance speed as in Figure 7, using the data in,¹⁷ which also provides the model for estimating the equivalent area $(A_{eqv})$ and the vehicle drag (D).

$D=\frac{1}{2}\rho V_{\infty }^2{A}_{eqv}\to A_{eqv}=\frac{2Wtan\left({\alpha }_r\right)}{\rho V_{\infty }}$ (12)

Figure 7 Quadratic approximation of data from¹⁷a for forward flight speed $\left(V_f\right)$ and drone inclination angle $\left({\alpha }_r\right)$

Figure 8 shows the force balance over each of the rotor of the drone, a quad-rotor configuration is considered. Steady horizontal flight is assumed, non-linear dynamics or control strategies are not considered, pitch moment equations are balanced by providing the same thrust, since the drone configuration has symmetrical arm lengths. As done in hovering, the rotational speed is the pilot input and is computed for ensuring the required thrust.

$\begin{array}{l}{\displaystyle \sum }_{i=1}^4{T}_i\sin \left({\alpha }_r\right)-D-H_{i}cos\left({\alpha }_r\right)=0\\ {\displaystyle \sum }_{i=1}^4{T}_i\cos \left({\alpha }_r\right)-W+H_{i}sin\left({\alpha }_r\right)=0\\ T_i=\frac{Wcos{\alpha }_r+Dsin{\alpha }_r}{4}\end{array}$ (13)

Finally, total power demands can be integrated using the differential power expression in equation 7. Additionally, in¹⁶ it is proposed and estimation of the split terms: induced power $\left(P_i\right)$ , parasite power $\left(P_0\right)$ . Vehicle drag power $(P_{par})$ must be added. As stated in,¹⁶ for profile drag computations, it can be quantified the effect of the reverse flow that appear in some azimuth positions $\left(\psi \in \left[\pi ,2\pi \right] \&r\in \left[0,{\mu }_{x}sin\psi \right]\right)$ . For that reason, it was used the coefficient $C_{rev}$ , which is 1 or -1 depending on if the flow.

$\begin{array}{l}P=P_i+P_0+P_{par}\\ P_i\approx \rho A_r{\left(\text{Ω}R\right)}^3{{\displaystyle \int }}_0^{2\pi }\frac{1}{2\pi }{{\displaystyle \int }}_0^1\frac{1}{2}\sigma {\left(\frac{U_T}{\text{Ω}R}\right)}^{2}Cl\lambda drd\psi \\ P_0\approx \rho A_r{\left(\text{Ω}R\right)}^3{{\displaystyle \int }}_0^{2\pi }\frac{1}{2\pi }{{\displaystyle \int }}_0^1\frac{1}{2}\sigma {\left(\frac{U_T}{\text{Ω}R}\right)}^{3}Cd{C}_{rev}rdrd\psi \\ P_{par}=D{V}_{\infty }\end{array}$ (14)

Figure 8 Rotor force balanced in forward flight scheme created using balance.

Validation

Hover validation

Hover validation was done using data from experimental test,¹⁷ Figure 9. Rmin is the first blade section.

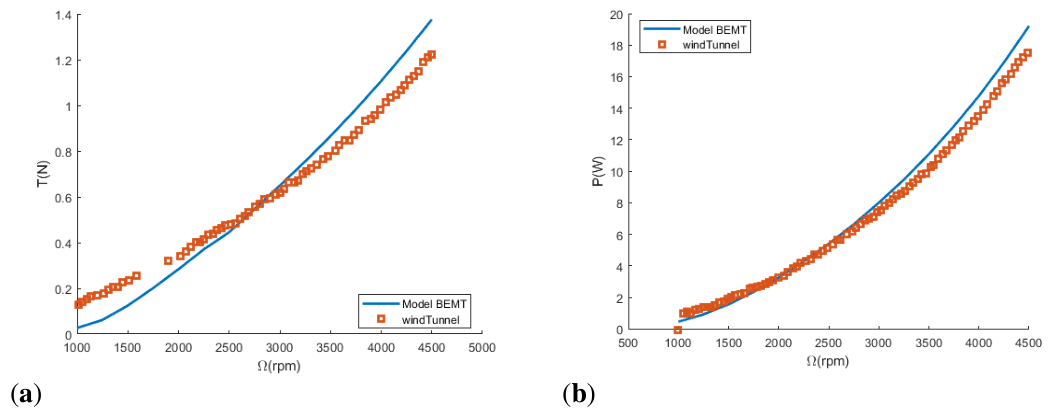
Figure 9 Comparison between model estimations and experimental data from18
(a) Thrust (N) versus rotational speed (Ω) rpm.

1. b=2
2. R=0.1775, Rmin=0.0845R.
3. Ω=1000-4500rpm.
4. c=0.0225, straight blade.
5. Linear twist θ_0=11 deg, Δθ=-10.833 deg
6. Airfoil NACA 0018.

Forward flight validation

Data from¹⁷ is used for forward flight model. Since no information about the chord distribution or twist was provided in the document, the data from a T18 rotor was used. Twist and chord distributions of the rotor are available in.¹⁹ Figure 10 shows the results.

1. Mass=2.13 kg
2. R=0.12m, Rmin=0.1R

Figure 10 Comparison between forward flight model Power (W) estimations versus forward flight speed (Vf(m/s)) and experimental data from.16

Power is underestimated for low velocities, however, as stated during the theoretical explanation, the model can only apply to cases in which $({\mu }_x>0.1)$ . Consequently, speed of 10 m/s was set as the minimum speed for optimizations.

Optimization

Among the available optimization methods, PatternSearch was chosen because it can handle robustly smooth and non-smooth problems with all kinds of boundary conditions²⁰ chapter 1.

Total rotor power was set as the objective function. Moreover, four chord and twist distributions were defined. They were combined resulting in 11 optimization cases performed at hovering for a supposed mass of 0.6 kg (1 rotor) and at forward flight for a quadrotor of 2.5 kg at three different advance speeds (10, 15, & 20 m/s). The baseline is a straight untwisted blade rotor with a radius (R) of 20 cm, a chord of 2 cm, and 10 deg pitch. Besides that, the optimization is constrained and bounded for avoiding negative pitch or chord. Additionally, a penalization is used for cases that do not fulfill the limitation ${\mu }_x\ge 0.1$ .

$f {\mu }_x<0.1\to P=P/{\mu }_x$ (15)

PatternSearch optimization is divided in 2 steps: mesh creation and polling. The default algorithm is GPS algorithm. It creates 2N searching vectors used for creating additional evaluation points, N is the number of independent optimization variables. Those are director vectors of dimension $1\times N:[\pm 1 \mathrm{0...}], [0\pm \mathrm{1...}]$ etc. The mesh is created using a scalar ${\text{Δ}}^{\text{m}}$ , which is the mesh size of default value 1. The points are created using the initial condition $\left(x_0\right)$ , the mesh size $\left({\Delta }^m\right)$ and the searching vectors $\left(v_i\right)$ .

$x_i=x_0+{\text{Δ}}^m{v}_i$ (16)

After that, the mesh is evaluated, that is called polling. By default, it evaluates until finding one point with a lower value than the original, successful poll, the new point is selected, and the mesh is expanded. Otherwise, the poll is unsuccessful, and the mesh size is reduced. Expansion and contraction factors are 2 and 0.5. The process is repeated until the stopping criteria is reached.

1. The mesh size is less than the MeshTolerance (1e-6).
2. Number of iterations reaches MaxIteration $\left(100\times N\right)$ .
3. Maximum number of function evaluations reached$\left(2000\times N\right)$
4. If after a successful poll, both, distance between initial and new point and mesh size is less than StepTolerance (1e-6).
5. If after a successful poll the change in the evaluation function is less than StepTolerance (1e-6).

Full information about PatternSearch and how it works can be found in MATLAB PDF documentation²⁰ chapter 6.

Twist and chord distributions and parameters

1. Linear twist and Linear chord parameters: root pitch and differential pitch (θ₀, slp) and root chord and tip/root chord ratio $\left(c_{root},tap\right)$ .

$\begin{array}{l}\theta \left(r\right)={\theta }_0+slp\cdot r\\ c\left(r\right)=c_{root}\left(1+r\left(tap-1\right)\right)\end{array}$ (17)

2. 2 Linear twist and Linear chord parameters: (θ₀, slp1, slp2, rper1) and $\left(c_{root},tap1,tap2,rper2\right)$ . Where is the blade section where segment changes.

$\begin{array}{l}\theta {\left(r\right)}_1={\theta }_0+\frac{slp1}{r_{perc1}}\cdot r, \theta {\left(r\right)}_2=\theta {\left(r_{perc1}\right)}_1+\frac{slp2}{1-r_{perc1}}\left(r-r_{perc1}\right)\\ c{\left(r\right)}_1=c_{root}\left(1+r\left(tap-1\right)\right), c{\left(r\right)}_2=c{\left(r_{perc2}\right)}_1\left(1+\frac{tap2-1}{1-r_{perc2}}\left(r-r_{perc2}\right)\right)\end{array}$ (18)

3. Quadratic twist and chord parameters: $\left({\theta }_0,c_{root},a_1, a_2\right)$ , (a) parameters control the chord/pitch at the tip.

$\begin{array}{l}\theta \left(r\right)={\theta }_0+a_1\cdot r^2-2a_1\cdot r\\ c\left(r\right)=c_{root}\left(1+a_2\cdot r^2-2a_2\cdot r\right)\end{array}$ (19)

4. Cubic Bezier twist parameters: (θ₀, θtip, r3, y4, r5, y6)→P0(0, θ0), P2(1, θtip), P1(r3, y4), P3(r5, y6), the parameters $\left(r,y\right)$ are the coordinates of the spline points.

$\theta \left(r\right)={\left(1-r\right)}^{3}P0+3{\left(1-r\right)}^{2}r\cdot P1+3\left(1-r\right)r^2\cdot P2+r^{3}P3$ (20)

5. Cubic Bezier chord parameters: $\left(c_{root},tap,r3,y4,r5,y6\right)\to P0\left(0,c_{root}\right),P2\left(1,tap·c_{root}\right),P1(r3,y4),P3(r5,y6)$

$c\left(r\right)={\left(1-r\right)}^{3}P0+3{\left(1-r\right)}^{2}r\cdot P1+3\left(1-r\right)r^2\cdot P2+r^{3}P3$ (21)

The bounds of the optimization variables are gathered in Tables 1 & 2. Where R is the radius of the rotor (20cm).

Additionally, the problem is constrained for avoiding negative pitch using inequalities.

1. Linear distribution: |Slp|-θ_root≤0
2. Quadratic distribution: a_1-θ_root≤0
3. 2. Linear distribution: |slp1+slp2|-θ_root≤0
4. Bézier distribution: $-\theta \left(r\right)\le 0\forall r\in \left[0,1\right]$

PatternSearch verifies that the points of the mesh fulfill the limits. If not, they are projected in the feasible subspace. The case of Bézier distribution limitation is more complex, nonlinear constraints problems are solved using Augmented Lagrangian Pattern Search (ALPS) algorithm, which solves several subproblems. ALPS algorithm combines penalization methods, who transforms a constrained problem into a non-constrained problem adding a penalization term, and lagrange methods for solving subproblems and reaching the optimal solution. This can be used for equality constraints and inequality constraints. The combination of both avoids problems with the penalization going to infinity for ensuring convergence. The general expression for the constrained subproblem with equalities $\left(ce{q}_i\right)$ , inequalities $\left(c_i\right)$ and penalization factor (ρ) is:

$\begin{array}{l}\text{Θ}\left(\text{x},\text{ λ},\text{ s},\text{ ρ}\right)=f\left(x\right)-{\displaystyle \sum }_{i=1}^m{\text{Λ}}_i{s}_i\log \left(s_i-c_i\left(x\right)\right)+ {\displaystyle \sum }_{i=m+1}^{mt}{\text{Λ}}_{i}ce{q}_i\left(x\right)\\ +\frac{\rho }{2}{\displaystyle \sum }_{i=m+1}^{mt}ce{q}_i{\left(x\right)}^2\end{array}$ (22)

The previous expression is the Lagrangian function of a constrained optimization problem with the addition of the penalization factor for the equality constraints. This subproblem is handled separately from upper and lower bounds and if required, linear constrains, which can be handled by projection of the points in the limits and subspaces. The subproblem expression considers the inequalities assuming the equivalence of the constraints $\left(c_i\le 0\right)$ and $\left(s_i\log \left(s_i-c_i\left(x\right)\right)\right)$ where $s_i$ are positive values known as shifts which are computed considering the penalty values (ρ) and the Lagrange multipliers estimates $\left({\text{Λ}}_{\text{i}}\right)$ . Moreover, this previous term ensures that the constraint inequality is fulfilled. As a global overview, what the inner algorithm responsible of solving the subproblem seeks is the convergence in a set of values $\left(x_k\right)$ that are first-order stationary points, or what is the same, a Kuhn-Tucker points. The algorithm is driven by the penalty factor, which is also used for estimating the Lagrange multipliers and convergence is reached if $\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\rho $}\right.\right)$ tends to a sufficiently small value. For deep details about the algorithm and the inequality constrained it is suggested to check MATLAB user guide documentation²⁰ as well as the article dedicated to Augmented Lagrangian Optimization with inequality constraints and bounds.²¹

Hovering optimization

Chord optimization, constant pitch of 10 deg: Tapered blades and quadratic chord distributions did not improve rotor efficiency in these regimes. Straight blade geometry was the optimal. Improving efficiency is represented by the term $\left(\Delta P=100\cdot (P_{opt}-P_{BL}\right)/P_{BL})$ , which is the percentual power reduction (-) or increment (+) with respect to the baseline rotor. Regarding to the distribution with two linear segments showed that hexagonal blade platforms can be an interesting alternative to straight blades. Finally, the spline distribution showed similar behavior to the previous distribution. The platform area is increased, and a slight taper is set near the tips, where speeds and profile drag are higher. Optimal parameters are in Table 3 whereas rotor’s comparative is found in Table 4.

Twist optimization, constant chord of 0.02 m:

Moving on to twist optimizations, the model predicts greater improvements for twisted blades. Additionally, the average blade pitch has been increased from the original pitch of 10 deg. This increment reduces the required rotational speed, thereby the profile drag. Furthermore, all distributions, except for the quadratic distribution, which is conditioned by its curve shape, show similar behavior, and have a comparable differential pitch between the root and tip. Like for large-scale rotors, twist optimal rate is negative. Parameters for each distribution and performance results are found in Tables 5 & 6, and they are plotted in Figure 11.

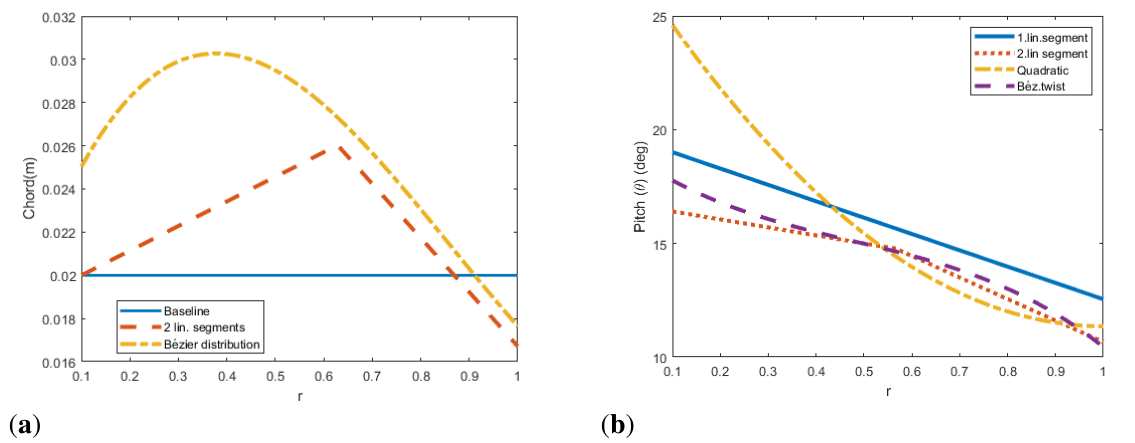
Figure 11 Isolated optimizations of chord and twist for hovering
(a) Optimal chord distributions (b) Optimal twist distributions.

Twist and chord optimization

Among the possible combinations of distributions, the optimization of bézier chord distribution was carried out with three different twist distributions: bézier twist, two linear segments twist, and quadratic twist. In general, quite similar chord distributions are observed for the three cases, Table 7, making clear the benefits of increasing the chord along the blade and reduce it again near the tips.

In terms of twist, Table 8, an interesting result is observed. The pitch is slightly increased near the root, followed by the typical negative rate. Notably, the 2 linear segment distribution has a flat zone, positive slopes were not permitted by the constraints. Distributions are plot in Figure 12.

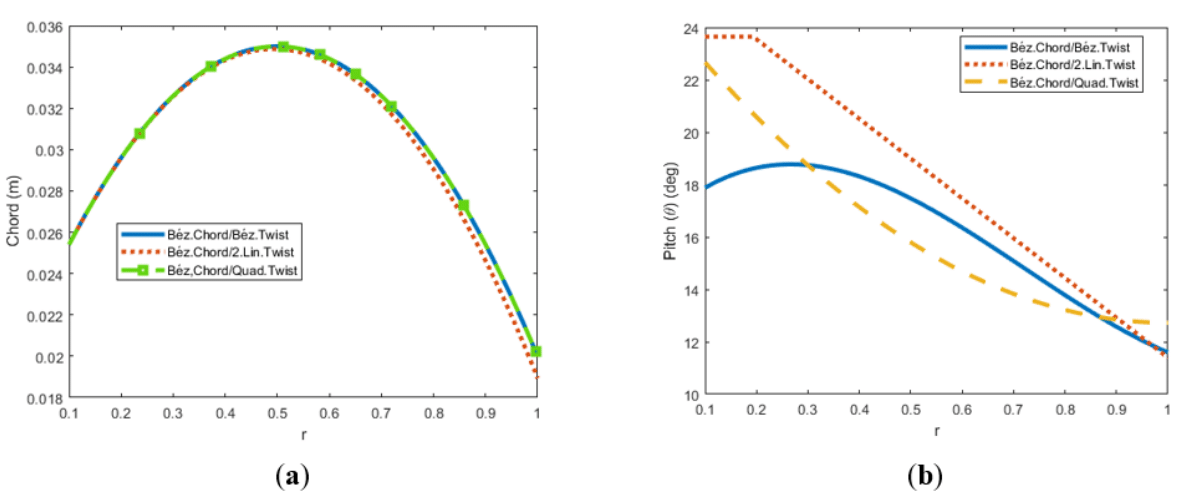
Figure 12 Combined optimizations of chord and twist for hovering
(a) Optimal chord distributions. (b) Optimal twist distributions.

Forward flight optimization

Chord optimization, constant pitch of 10 deg

Linear case and quadratic chord, 2 parameters: As it happened for hovering, the straight blade was the optimal solution for all the cases and velocities. Table 9 shows the parameters of the baseline rotor, the geometry achieved. For the quadratic case, the parameter $\left(a_2\right)$ was zero for all analyzed cases. Hence, straight blade geometry is preferred rather than a quadratic tapered $\left(c_{root}>c_{tip}\right)$ distribution.

2 linear segments case, 4 parameters:

First differences appear. Table 10 gathers the results for hexagonal blades. Regarding to the case of 20 m/s, with the fixed constant pitch and the radius of the blade defined, no platforms could be found that provided the required thrust without violating the condition of $\left({\mu }_x\ge 0.1\right)$ . Figure 13(a) shows the distributions.

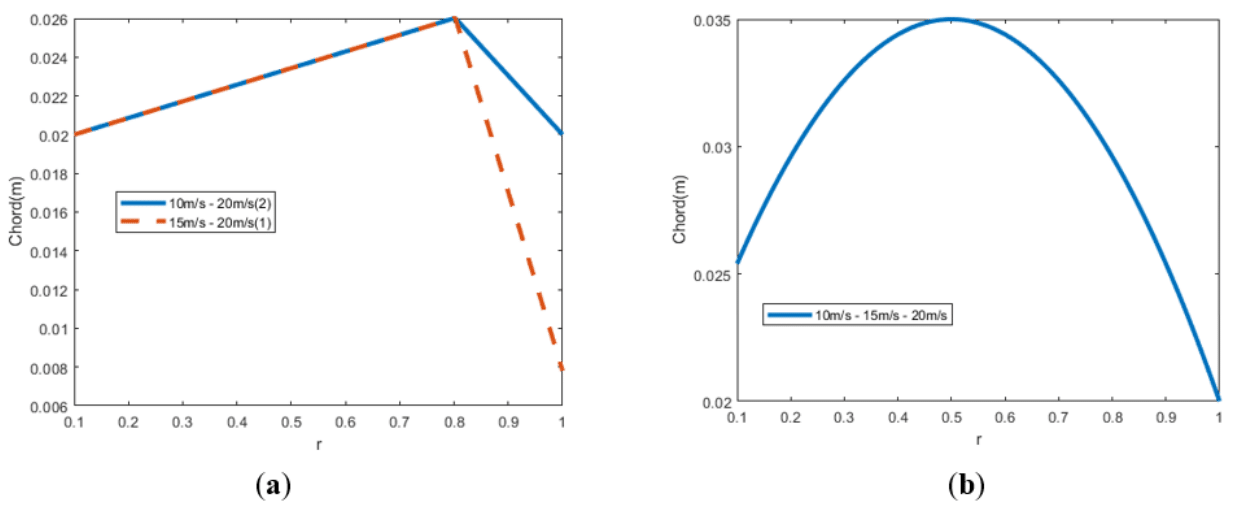
Figure 13 Isolated chord optimization for forward flight
(a) Optimal 2. linear chord distributions. (b) Optimal Bézier distributions.

Bézier cubic curve, 6 parameters:

The difference between the solutions is only the radial coordinate of the control points of the curve, however, the sensitivity of the function is not that big (Table 11), so the coordinates do not have an impact. Similarly to the previous case, the platform surface is increased, Figure 13(b).

Twist optimization, constant chord of 0.02 m

By contrast to the chord optimization, for which the optimal solution was barely the same regardless of the speed case. For twist, differences are found in the pitch variation between root and tip and, for some cases, in the curvature of the whole distribution.

Linear case, 2 parameters:

As it is frequent, the twist rate is negative. Moreover, for the case of 20 m/s, the differential pitch is smaller. More constant pitch is required due to high thrust demands. Regarding the other cases, pitch near the tip is barely zero, it is observed the influence of the tip losses. Those sections of the blade barely provide lift so a big pitch would only mean more drag without benefits for lift generation, Table 12, and Figure 14(a).

Quadratic case, 2 parameters:

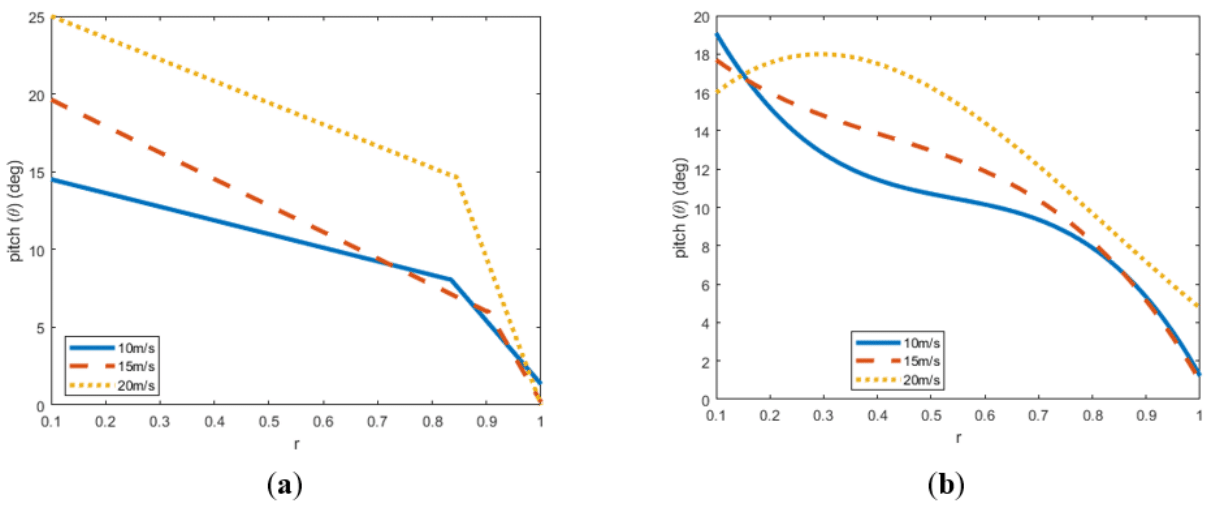
Figure 14 Isolated twist optimization for forward flight
(a) Optimal 2 linear twist distributions. (b) Optimal Bézier distributions.

Like in the linear case, increasing the forward speed tends to result in a flatter pitch distribution. See Table 13 and Figure 14(b).

2 linear cases, 4 parameters:

All solutions share the same behavior. First segment’s slope is less negative than near the tip. Near the tip, a steep pitch reduction is observed for all the cases until almost zero pitch, therefore, reducing the lift in the tip. Results are showed in Table 14 and Figure 15(a).

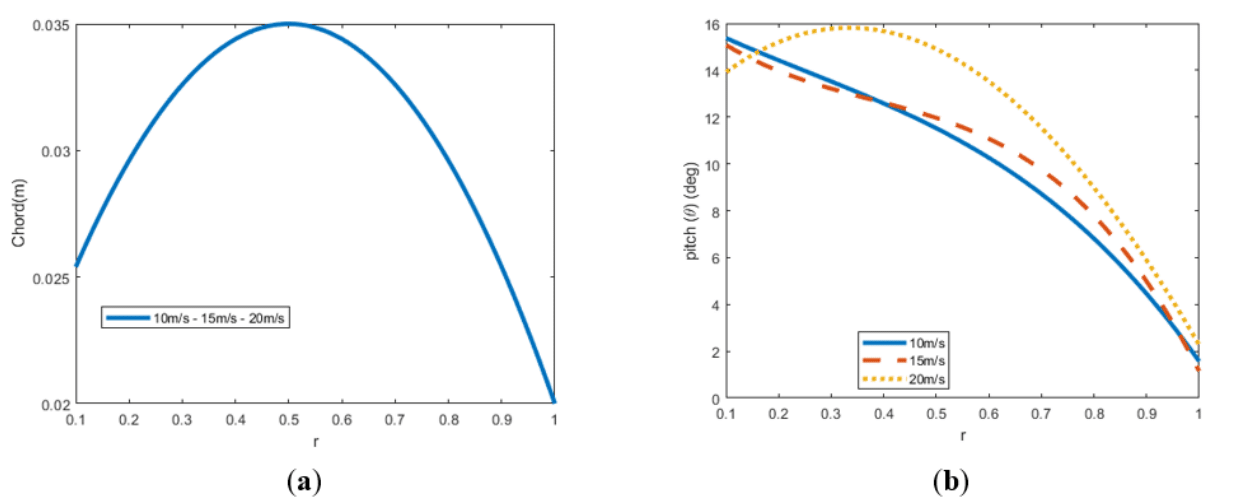
Figure 15 Combined optimizations of Bezier chord and Bezier twist distributions for forward flight
(a) Optimal chord distributions (b) Optimal twist distributions.

Bézier cubic curve, 6 parameters:

For the two first speeds analyzed show similar results to the previous ones, a clear negative twist, the middle zone of the blade shows flatter distributions whereas near to the tip the pitch approaches to zero rapidly. By contrast, the case of 20 m/s shows a particular opposite tendency for sections closer to the root where the pitch is increased. See the results in Table 15 and Figure 15(b).

Twist and chord optimization

Bézier chord and Bézier twist, 12 parameters:

The chord distributions obtained are identical to those obtained through isolated resolution, in which the optimal distribution was increasing the platform area. Parameters and the representation are in Table 16 and Figure 16.

Figure 16 Combined optimizations of Bezier chord and quadratic twist distributions for forward flight
(a) Optimal chord distributions (b) Optimal twist distributions.

Optimal twist distributions show slight differences compared to those obtained without chord optimization, Table 17. Two first distributions are quite similar one to the other. Apart from that, the pitch for 20 m/s case, decreases faster near to the tip than it was for the previous study. Distributions are displayed in Figure 16.

Quadratic twist and Bezier chord, 8 parameters:

Only the 3rd considered speed scenario shows interesting variations. For detailed results check Tables 18 & 19 and Figure 17.

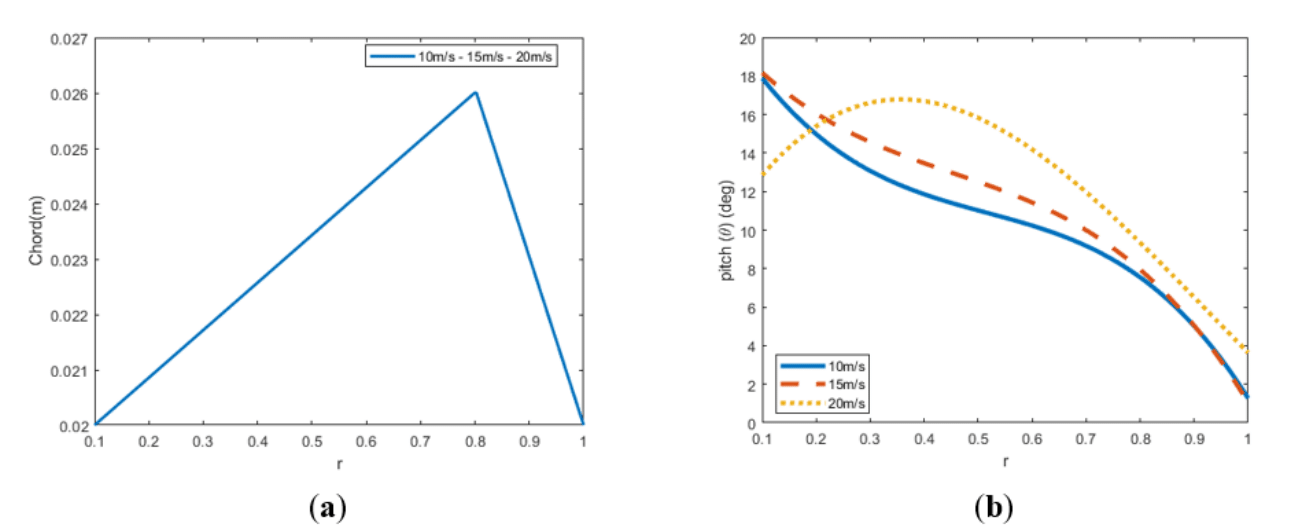
Figure 17 Combined optimizations of 2 linear chord and Bezier twist distributions for forward flight
(a) Optimal chord distributions (b) Optimal twist distributions.

In terms of pitch. Again, 20 m/s case is the one showing relevant discrepancies to previous results. Before, for the quadratic distribution it was already noticed that the distribution was flatter for this speed, however, now with the addition of the chord distribution, the parabola it is even flatter, and the pitch remains on average quite constant over the blade. Also, this can be related with the necessity if a smaller blade surface for generating the required thrust, mainly because on average the pitch is bigger, so more lift is produced.

Bézier twist and 2 linear chord, 10 parameters:

As it happened during the optimization of chords following this distribution, the tendencies are again to increase the surface available for lift generation creating hexagonal blades. Results in Table 20 & 21 and Figure 18.

Figure 18 Fluid domains and boundary conditions
(a) Hovering simulations (b) Forward flight simulations.

For the pitch, the distributions remain quite the same to the previous ones.

In terms of power reduction, all cases show enhanced performance compared to the baseline. Moreover, the combination of chord and twist seems to be better than just modifying one parameter, as it happens with large scale rotors. However, obtained results show large improvements in terms of power consumption. Those results might be quite optimistic, and they must be verified against CFD simulations.

CFD simulations

Set up and previous studies

As previously mentioned, CFD simulations are used for verification of the obtained results and models. Complex 3D phenomena and other aspects difficult to quantifies theoretically can be approached with these tools. Within the domain of CFD, there are usually more than one approach for the same kind of problem. As stated during the introduction, rotary flows can be treated with three methods. The setup of the simulations as well as the fluid domain geometry depend on the course of action for tackling up the issue. Among the possible alternatives, Multiple reference frame (MRF) has been chosen for solving hover simulations, as it was done by R.Cagnato.¹ This strategy allows simulating the problem in quasi-steady approach without needing transient simulations by using a static absolute frame and a rotational frame. MRF can only be applied to constant rotational flows and Navier-Stokes equations are solved considering the relative velocities between frames.¹

On the other hand, for addressing forward flight, transient simulations are required. Sliding mesh will be used. Prior to this, other researchers obtained satisfactory results by this method.⁷ Sliding mesh is selected since forward flight flow requires a more accurate time solution due to flow variation over the revolution. Concerning to the turbulent model, based on the preferences in prior projects, k − ω SST has been chosen for hovering and forward flight. This model can transition automatically from viscous sublayer to logarithmic layer. Furthermore, it is suitable for low Reynolds regime, and it is possible to activate a third equation for addressing the possible transition between laminar to turbulent flow.²²

Fluid domain configuration

For hover simulations, two cylindrical domains are created: one surrounds the rotor and represents the fluid zone linked to the rotary reference frame, while the other represents the static zone and is linked to the absolute frame of reference. The dimensions, Table 22, of both zones are defined based on the dimensional analysis available in.¹⁷

For forward flight simulations. The rotary domain is represented by a cylinder. However, the static domain is a rectangular prism. Moreover, an extra rectangular box was used for grid refinement tasks near the interface between domains. The dimensions have been determined based on prior studies.^7,23 Table 23 shows the dimensions of the domains.

Boundary conditions and set up

The top base of the static cylinder is designated as a pressure inlet, while the bottom is set as a pressure outlet. Symmetry conditions are applied to the lateral surface to prevent perpendicular flow or convection. The shared surface between fluid zones is declared as an interface and rotor surface as a moving wall with no-slip condition and zero relative speed to adjacent cell zones. The rest of set up configurations follows R. Cagnato procedure,¹ which are based on Ansys guidelines. Computations are performed using absolute reference frame with Pressure solver, velocity-pressure coupling is solved using the COUPLED method because of its robustness converging. Discretization is set using second order upwind for more accuracy, except for pressure, which uses the PRESTO scheme.

For forward flight simulations, all faces except the backward are set as velocity inlets, defined by the flow magnitude and direction, allowing consideration of various rotor inclinations. The backward surface is a pressure outlet. Inner box solid is just used for grid discretization. Static-rotational cylinder iteration is defined as an interface and rotor surface is set as a moving wall with no-slip condition and zero relative velocity to adjacent cell zone. COUPLED is again selected to solve the differential equation system, with second order upwind used for discretization. Figure 19 shows the defined fluid domains and the boundary conditions.

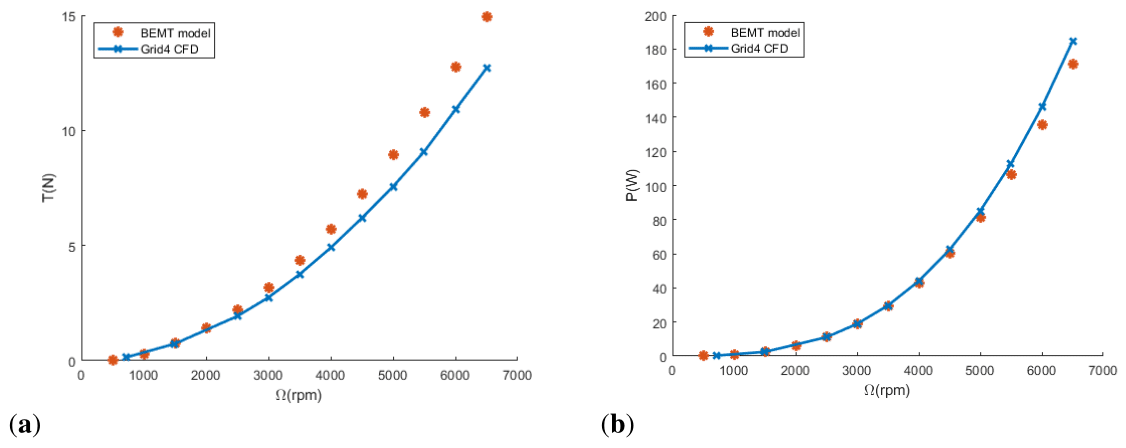
Figure 19 Comparison between model estimations and CFD simulations of the baseline rotor at hovering flight (a) Thrust (N) versus rotational speed $\left(\text{Ω}\left(\text{rpm}\right)\right)$ . (b) Power (W) versus rotational speed $\left(\text{Ω}\left(\text{rpm}\right)\right)$ .

Grids and time step analysis

For both cases, an unstructured grid was chosen due to its semi-automatic generation and proven ability to yield good results. To ensure proper capture of the boundary layer, inflation with multiple prismatic layers was applied around the rotor blades. The first layer thickness was set to 5e-6 meters to maintain a wall y+ ∼ 1.

Grid analysis was performed for both simulations to ensure grid independence and reach a balance between time and accuracy, crucial for forward flight simulations, which demanded a high computational cost. Results are shown in Table 24 &25.

It is concluded that a medium-fine grid should be sufficient, as the variations with the finest mesh are lower than 5% for both cases.

Moving on to forward flight grids, it must be checked the grid independence and the required time step. These simulations must be done transiently, which requires high simulation time. Additionally, to prevent convergence issues and ensure stability, it is mandatory to use an appropriate time step. Priorly, in,⁸ for hovering sliding mesh simulation, a time step equivalent to $\psi =4$ deg was enough. However, in forward flight, other researchers performed simulations with smaller time steps within the range of $\Delta \psi =1$ deg.⁷ Results of the step-time analysis showed in Table 26.

After the studies, it is concluded that a medium grid combined with a time step of $\Delta \psi =2$ deg is a compromise solution. With this combination, the time required per simulation (four full rotations until report convergence) was approximately 19 h.

Hover simulations

The baseline rotor was simulated at several rotational speeds. In general, model and CFD simulations show similar results. The model based on BEMT seems suitable for estimating rotor performance capacities in hover. The theoretical model overestimates thrust capacities and under predicts power requirements, still, good predictions are yielded. Figure 20 shows the results and the inflow distribution is analyzed in Figure 21.

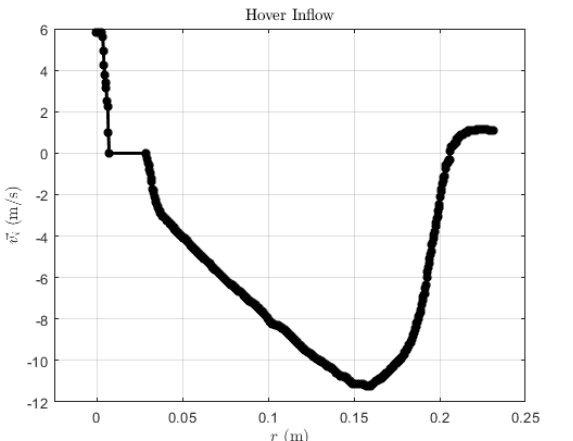
Figure 20 Inflow speed distribution $\left(\overrightarrow{v_i}\right)$ along the blade from CFD simulations at hovering.

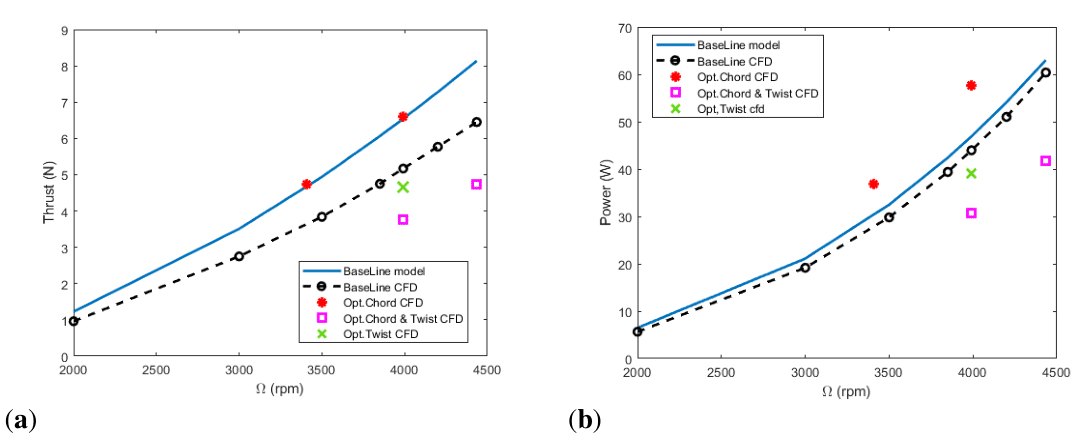
Figure 21 Comparison between model estimations and CFD simulations of the baseline rotor and some optimal rotors at forward flight
(a) Thrust (N) versus rotational speed $\left(\text{Ω}\left(\text{rpm}\right)\right)$ (b) Power (W) versus rotational speed $\left(\text{Ω}\left(\text{rpm}\right)\right)$ . /p>

The induced speed distribution shows the effect of the hub, near to the root the induced speed goes to zero. Moreover, it is observed the presence of tip vortexes, there is an upward inflow at the tips because of the circulating flow due to the difference of pressure between bottom and upper zones.

Forward flight simulations

The baseline rotor was simulated at multiple rotational speeds to obtain the evolution of thrust and power at different pilot inputs. Additionally, the best optimal geometries were simulated at the rotational speed estimated for providing enough thrust for the drone model and at the same operational speed than the baseline. It is observed that the model is overestimating the thrust with errors of the order of 20%, Figure 22.

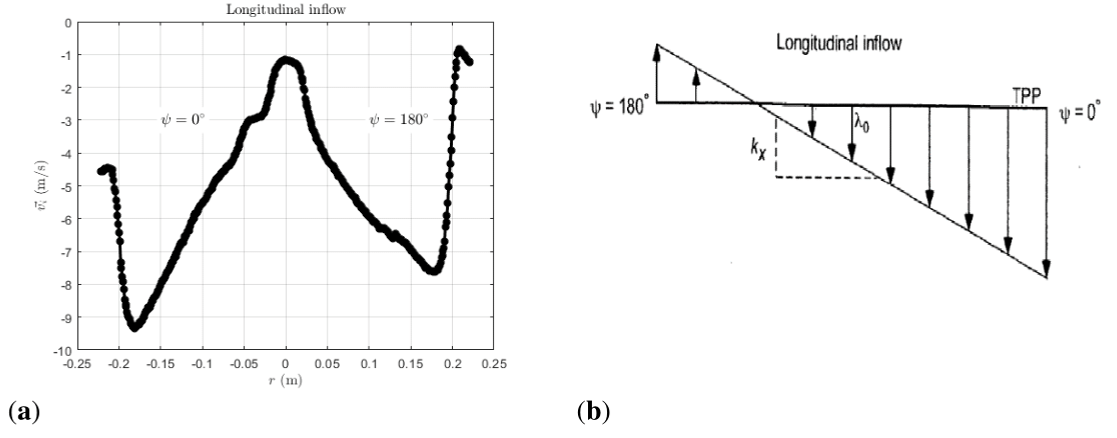
Figure 22 Comparison between inflows distributions from CFD simulations and theoretical lineal model16 at forward flight
(a) CFD longitudinal inflow $\left(\overrightarrow{v_i}\left(m/s\right)\right)$ . (b) Theoretical longitudinal linear inflow distribution.

Overestimation of thrust may be related to some sources of error. Firstly, as it was pointed out, XFOIL estimations for airfoil aerodynamic coefficients tends to be optimistic with lift capabilities and stall point prediction, as it can be observed in Figure 1. Besides that, the model and the simulations tend to diverge as rotational speed is increased, already during optimization problems with the applicability of the theory were observed, since the theory can only be applied for $\mu x\ge 0.1$ . The operational speeds computed for each of the optimized rotors are closed to this limit of 0.1. Finally, the model is being applied for high pitch of the rotor, whereas when the theory is applied to large scale rotors for which the rotor pitch is usually a small angle. The bigger the inclination, the closer to an axial flight regime. Moreover, it is observed that the over-prediction of thrust is even bigger for the rotor geometries with variable pitch along the blades. As seen in the analysis of the optimized rotors, the twist distributions lead to very low pitch angles near to the tip due to the presence of losses, however, this is affecting considerably to the lift generation and simulations are not reflecting the estimated reduction in power by decreasing the pitch.

If the power requirements are compared, Table 27, it is observed that some of the geometries, that were supposed to enhance the baseline capabilities, are far for reaching the predicted improvements, particularly for the cases related with twist optimization.

The optimization of the chord distribution provides a benefit in terms of power requirements. However, the rotor with variable pitch and constant chord does not improve the baseline and the combination of chord and twist shows negligible improvements. The improvement predictions of the model were only achieved for the chord optimization.

During the simulations, it was obtained the induced speed over the blades at multiple azimuth positions. As explained, the inflow was assumed to be linear. However, at the simulations, high non-uniform inflows were obtained. The inflow is far from the linear distribution assumed for longitudinal $\left(\psi =0,180deg\right)$ and lateral (90,270 deg) positions, as depicted in Figures 23 &24.

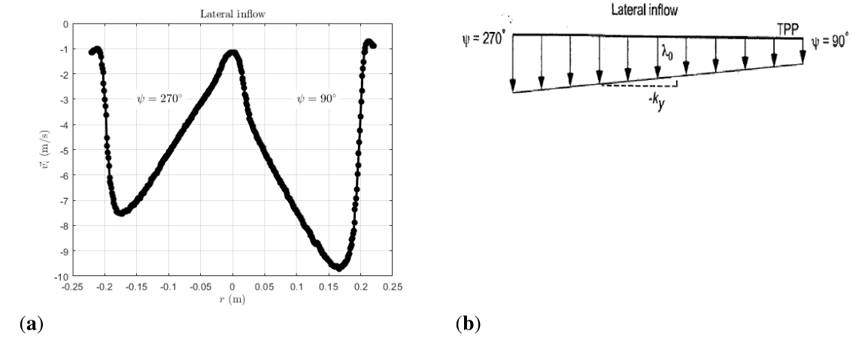
Figure 23 Comparison between inflows distributions from CFD simulations and theoretical lineal model16 at forward flight:
(a) CFD lateral inflow $\left(\overrightarrow{v_i}\left(m/s\right)\right)$ . (b) Theoretical lateral linear inflow distribution.

Figure 24 Comparison between original inflow model and modified inflow model based on CFD simulations:
(a) Original longitudinal inflow$\left(\overrightarrow{v_i}\left(m/s\right)\right)$ (b) Modified longitudinal inflow $\left(\overrightarrow{v_i}\left(m/s\right)\right)$ .

The estimation of the inflow affects the predictions having a bigger impact on the pitch optimization than on chord because the pitch is used to set the airfoils at maximum aerodynamic efficiency whereas the chord optimization is linked with profile drag and lift generation by available surface. Regarding to tip/hub losses, by contrast to hovering where upwash was observed near the tip. At these inflows though the downwash is reduced, the flow is far from changing its direction. This can be related with the presence of a lighter effect of tip vortexes. To check if this could have a substantial impact on the model, some modifications were performed. First, the tip/hub losses were removed, meaning that, it is assumed that the tip/hub sections can generate lift. Moreover, the linear models were modified to try to estimate inflows more like the predicted with the simulations. The modification of the inflow model was done with some simple changes. Figures 25 & 26 shows the comparison between original and modified models.

Figure 25 Comparison between original inflow model and modified inflow model based on CFD simulations:
(a) Original lateral inflow $\left(\overrightarrow{v_i}\left(m/s\right)\right)$ . (b) Modified lateral inflow $\left(\overrightarrow{v_i}\left(m/s\right)\right)$ .

Figure 26 Isolated optimizations of chord and twist for forward flight at 10 m/s with the modified model
(a) Optimal chord distributions. (b) Optimal twist distributions.

1. Firstly, since a certain degree of symmetry is observed with respect to the azimuth position, the absolute value of the azimuth angle is considered in the equation 11.
2. Secondly, lateral, and horizontal inflow is similar than. Pitt & Peters model assumes constant inflow for lateral inflow, Equation 11, however, for approximating the simulations, it is used the longitudinal inflow coefficient $\left(k_x\right)$ .
3. Finally, since both blades showed different initial inflow values but only slightly different slopes, it is applied a sigmoid function between the opposite azimuth angles. Smoothly reducing the initial inflow and varying slightly the slope.

After that, optimization was run again for the case of $V_f=10m/s$ . Regarding to chord optimization, no significant changes were found with the linear and quadratic distributions, which still are worse than the baseline. Two linear segment distributions were the same than the obtained in the first optimization, Table 11, and Figure 13. Regarding to Bézier, almost no changes are observed, results are in Table 28.

With respects to twist, some interesting results were achieved, new distributions differ to the previous from the original model. Parameters are gathered in Table 29 whereas Figure 27 shows the distributions.

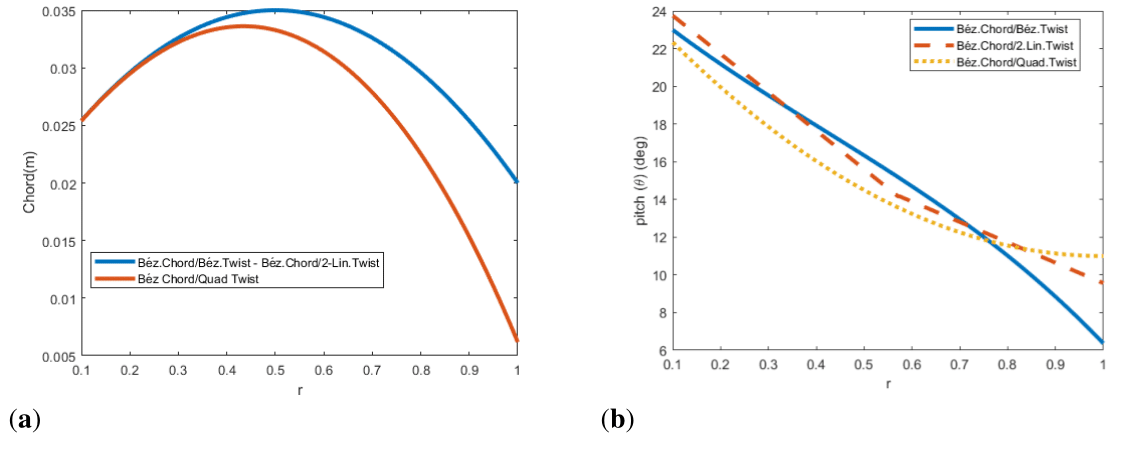
Figure 27 Combined optimizations of chord and twist distributions for forward flight at 10 m/s
(a) Optimal chord distributions. (b) Optimal twist distributions.

The new twist rate in all distributions is more moderate and the airfoils near the tip are set with bigger pitch angles. Apart from that, the spline distribution shows a quite linear behavior.

Moreover, it was performed the dual optimization of chord and twist. Whose results are shown in Tables 30 & 31. General tendencies analyzed before are observed again, negative twist enhances the performance, twist implementation helps setting the airfoils at angle of attacks for which aerodynamic efficiency is high, as it approaches to the tip, the inflow angle $\left(\varphi =\text{atan}(U_P/U_T)\right)$ decreases as a consequence of the higher tangential speed that increases faster than the induced speed. Hence, the required pitch for keeping a moderate angle of attack is smaller, as a result of this, the same thrust is generated with lower rotational required speed than the baseline, which affects the drag, as reflected in Table 5 for hovering and by Figure 28(a). With respects to chord, it is increased in middle sections of the blades and reduce near the tips were drag is bigger. As mentioned during the introduction, the benefit of the larger chords is linked with the higher Reynolds regime over the blades. Particularly, thick airfoils with non-ideal designed for operating at these regimes, such as the used NACA 0012, increased their efficiency rapidly even with small variations of the Reynolds regime. Moreover, despite this effect cannot be considered since the data base is fixed, the chord variation would have an impact on the thickness ratio of the airfoils, making them more slender bodies, which as stated by other researchers that did analyze the optimization of the airfoils,⁴ is interesting at low Reynolds regimes. Further justification and explanation of the optimal shapes would require a more thorough analysis, CFD simulations can also be used for studying the physics around the blades and can be used for studying the wake and checking distributions such as lift or pressure along the blade.

These new geometries were simulated in CFD and the estimations for the baseline were compared with the new model predictions. Figure 28 shows the comparative between the simulations and the estimations form the modified model.

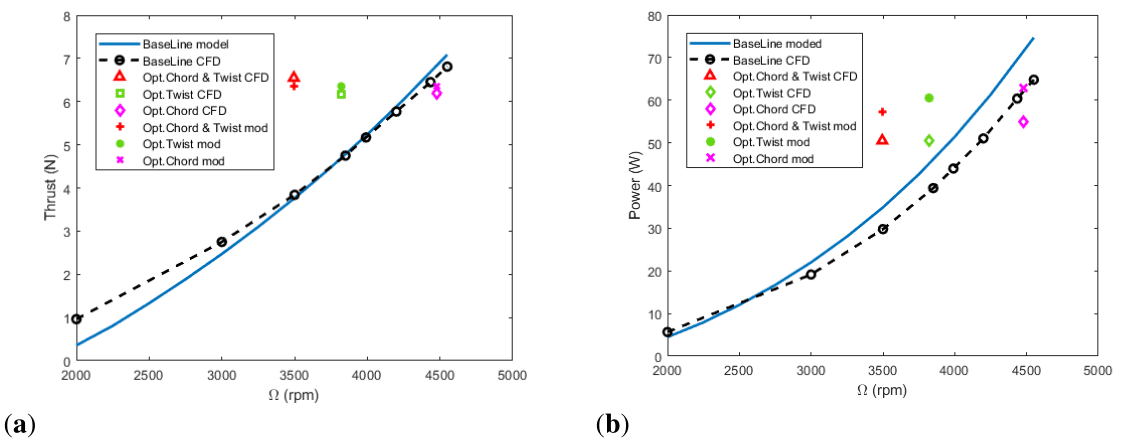
Figure 28 Comparison between modified model estimations and CFD simulations of the baseline rotor and some optimal rotors at forward flight
(a) Thrust (N) versus rotational speed $\left(\text{Ω}\left(\text{rpm}\right)\right)$ . (b) Power (W) versus rotational speed $\left(\text{Ω}\left(\text{rpm}\right)\right)$ .

It is observed that the overestimation of thrust has been reduced. Furthermore, opposite to previous optimization, the new geometries enhance the performance of the baseline rotor, as estimated by the model. The Table 32 shows the estimations of power of each of the geometries and the power reduction with respect to the baseline as well as the estimated pilot input for reaching that performance.

New model predicts improvements from the baseline geometry, however, despite it happened before, the power reductions are more conservative, and they seem less optimistic than the previous ones. Table 33 shows the same results but obtained from CFD simulations.

Clearly, the modifications in the model provide more accurate results. The power reductions estimated are confirmed with the CFD simulations.

The present study assessed the feasibility of developing low-fidelity models for small-scale rotors as a cost-effective alternative to more expensive tools. The model based on BEMT for hovering, implemented in MATLAB using XFOIL for airfoil properties, showed good agreement with CFD simulations. The second model for forward flight, however, overestimated thrust generation and power reduction of variable pitch rotors. The proposed chord optimizations improved baseline performance, but variable pitch benefits were not reflected in the simulations. Simulations showed non-uniform inflows contradicting linear theoretical models. Adjusting the inflow reduced thrust overestimation but continued to predict lower power demands with decreased pitch near tips. 3D losses functions direct applicability for forward flight was uncertain, hence, they were removed from the model. New optimized geometries resulted in different pitch distributions without affecting chord distributions. CFD simulations agree with

would be the impact on the thickness ratio of the airfoils. Optimizations predicted power reductions of 3−4% for chord, 7−11% for twist, and up to 17% for combined distributions.

Despite CFD is a higher fidelity tool than theoretical models, it would be interesting to perform wind tunnel tests for checking the results. the new model predictions.

In summary, linear inflow assumptions were invalidated by CFD results, impacting rotor performance predictions. Hub/tip losses models' applicability in forward flight remains uncertain. Variable chord and pitch distributions offer potential improvements in small-scale rotor designs. As it happens for large scale rotors, negative twist implementation shows promising results for reducing power demands. The variation of pitch along the blade try to set all the airfoils sections at angles of attack with better aerodynamic efficiency. In terms of chord distributions, by contrast to large scale rotors, for which tapered blades are common, for small scale rotors seems interesting a concave shape. Increasing the chord implies bigger Reynolds over the blade, which enhances airfoil aerodynamic efficiency due to the low Reynolds regime, in which small changes have an important impact on the lift/drag ratio, another positive effect that cannot be quantified Moreover, CFD simulations were performed focusing on validating the models, but they can also be used as a tool for analyzing thoroughly the physics and impact of the geometrical changes on the flow over the blades. Additionally, the created models can be used for analyzing other sizes of rotors for heavier vehicles apart from studying other parameters such as the number of blades as well as they can be used as a base for implementing new parametrical effects considerations such as tip shapes effects.

The authors acknowledge the support of Fundação para a Ciência e a Tecnologia (FCT), through IDMEC, under LAETA, with grant number (UIDB/50022/2020).

The authors declare that there is no conflict of interest.

1. Cagnato R. Study on the effect of curvature on the aerodynamic properties of drone rotor blades. Master Thesis, Master of Science Degree in Aerospace Engineering-Instituto Técnico Superior, Universidad de Lisboa; 2020.
2. Caceres Andrade CA. Design of an aerodynamic profile for low Reynolds numbers using computational tools. Final Degree Project, Degree in Mechanical Engineering-Universidad de Pamplona; Colombia: 2021.
3. Walsh JL. Performance optimization of helicopter rotor blades. Proceedings of the Air Force/NASA Symposium on Recent Advances in Multi-Disciplinary Analyses and Optimization; 1990 September 24-26; San Francisco, CA, United States: NASA; 1991.
4. Bohorquez F. Rotor hover performance and system design of an efficient coaxial rotary wing micro air vehicle. Doctoral dissertation, College Park: University of Maryland; 2007.
5. Winslow J, Otsuka H, Govindarajan B, et al. Basic understanding of airfoil characteristics at low Reynolds Numbers (104–105). J Aircraft. 2017;55:1050–1061.
6. Wiebe J. Development of a simulation and optimization framework for improved aerodynamic performance of R/C helicopter rotor blades. Master Thesis, Master of Applied Science in Aerospace Engineering, Ottawa: Carleton Institute for Mechanical and Aerospace Engineering; 2015.
7. Kodchaniphaphong C, Pukrushpan J, Klumpol C. Investigating and analyzing the potential for regenerating excess energy in a helicopter UAV. Drones. 2023;7(10):643.
8. Fernandes de Vasconcelos CH. Aerodynamic effect of different drone blade tip shapes. Master thesis, Master of Science Degree in Aerospace Engineering-Instituto Superior Técnico, University of Lisbon; 2023.
9. The MathWorks Inc. MATLAB version: 9.13.0 (R2022b), Natick, Massachusetts: 2022.
10. Drela M. XFOIL version 6.99, Cambridge, Massachusetts: Massachusetts Institute of Technology; 2000.
11. Ansys Inc. Ansys fluent version 2021 R2, Canonsburg, Pennsylvania: 2021.
12. Pelletier A, Mueller TJ. Low Reynolds Number aerodynamics of low-aspect-ratio, thin/flat/cambered-plate wings. J Aircraft. 2000;37:825–832.
13. Ohtake T, Nakae Y, Motohashi T. Nonlinearity of the aerodynamic characteristics of NACA0012 Aerofoil at Low Reynolds Numbers. J Japan Soc Aeronaut Space Sci. 2007;55(644):439–445.
14. Ahmad M, Li B. A comparative analysis of turbulence models in FLUENT for high-lift airfoils at low Reynolds Number. In: International Conference on Unmanned Aircraft Systems (ICUAS); 2022. p. 779–786.
15. Drela M. XFOIL: An analysis and design system for low Reynolds Number airfoils. In: Conference on Low Reynolds Number Airfoil Aerodynamics; 1989 June 5-7; University of Notre Dame; Indiana, USA: 1989.
16. Leishman JG. Principles of helicopter aerodynamics. 2nd ed. In: Cambridge Aerospace Series. 32 Avenue of the Americas, New York, NY 10013-2473, USA: Cambridge University Press; 2006. p. 60–273.
17. Theys B, De Schutter J. Forward flight tests of a quadcopter unmanned aerial vehicle with various spherical body diameters. International Journal of Micro Air Vehicles. 2020;12.
18. Zabotto Chiusoli R. Experimental study of modifications of drone propeller blades for noise reduction and performance. Master thesis, Master of Science Degree in Aerospace Engineering- Instituto Superior Técnico, University of Lisbon; 2023.
19. Kolaei A, Barcelos D, Bramesfeld G. Experimental analysis of a small-scale rotor at various inflow angles. Int J Aerospace Eng. 2018;2560370.
20. The MathWorks Inc. MATLAB global optimization toolbox user’s guide R2024, Natick, Massachusetts: 2024.
21. Conn AR, Gould N, Toint PL. A globally convergent augmented lagrangian barrier algorithm for optimization with general inequality constraints and simple bounds. Mathematics of Computation. 1997;66(217):261–288.
22. K-Omega Turbulence Models; SimScale.
23. Nathanael JC, Wang JC, Low KH. Numerical studies on modelling the near and far field wake vortex of a quadrotor in forward flight. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering. 2022;236(6):1166–1183.