Analysis of the oscillatory taylor-culick flow using the multiple time scale method

doi:10.15406/aaoaj.2017.01.00014

eISSN: 2576-4500

Aeronautics and Aerospace Open Access Journal

Research Article Volume 1 Issue 3

Analysis of the oscillatory taylor-culick flow using the multiple time scale method

Yi Che, Liu Pei Jin

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Science and Technology on Combustion, Northwestern Polytechnical University, China

Correspondence: Liu Pei Jin, Science and Technology on Combustion, Internal Flow and Thermal-Structure Laboratory, Northwestern Polytechnical University, Xi'an, China

Received: September 08, 2017 | Published: October 24, 2017

Citation: Che Y, Peijin L. Analysis of the oscillatory taylor-culick flow using the multiple time scale method. Aeron Aero Open Access J. 2017;1(3):108-114. DOI: 10.15406/aaoaj.2017.01.00014

Download PDF

Abstract

The pressure oscillations of the solid rocket motor could reduce the performance of rocket motors and damage the payloads. Therefore, it is required to predict the conditions leading to turbulent transition from near-laminar to a turbulent flow in the vicinity of the propellant surface, and it is a problem of hydrodynamic instability. In this work, linear stability theory together with the spectral collocation method has been applied on the biglobal hydrodynamic stability analysis of the oscillatory Taylor-Culick flow. Setting the time scale of the basic flow and the hydrodynamic mode as the slow time and the fast time respectively, the linear stability equations are solved using the multiple time scale method. The biglobal hydrodynamic modes are obtained, and the results show that the maximum growth rate of the hydrodynamic mode and its corresponding frequency vary in one period of the basic flow. Furthermore, the parametric study, including the amplitude and the frequency of acoustic motions, is also carried out. The results show that an increase in the amplitude and the frequency of acoustic motions can both make the flow more unstable.

Keywords: biglobal stability analysis, multiple time scale method, taylor-culick flow, hydrodynamic instability, prerequisite condition, eigenvalues

Introduction

Research has shown that oscillatory or modulated flows can achieve a significant increase in heat transfer relative to the corresponding steady flow, providing that critical or threshold amplitude is achieved. The threshold condition is associated with the production of near-surface turbulence by the oscillatory motion. A similar process is hypothesized as a mechanism of high-amplitude acoustic instability in solid propellant rockets, wherein finite amplitude acoustic motions can produce near-surface turbulence and lead to an enhanced propellant burning rate that couples with the chamber acoustics. Prediction of the threshold acoustic amplitude of propellant response requires prediction of the conditions leading to turbulent transition from near-laminar to a turbulent flow in the vicinity of the propellant surface as a prerequisite condition, and is thus a vicinity of the propellant surface as a prerequisite condition, and is thus a problem of hydrodynamic instability.¹

Two principal analytical approaches have been applied in the literature to the problem of hydrodynamic stability of time-dependent flows. These are the multiple (time) scales approach^1,2 and Floquet expansion approach. Von Kerczek and Davis² and Hall³ applied the formal Floquet theory to a simple Stokes layer and their results showed that the flow is stable for all Reynolds numbers investigated, in contradiction with experimental results. Singer⁴ compared the results of the numerical simulation and the linear stability analysis of oscillatory plane channel flow, and concluded that interpreting the stability results in the Floquet sense may not be appropriate for the flow that undergoes large transient growth (and decay) of the disturbances. However, Blennerhassett^5,6 obtained the unstable modes of Stokes layer while increasing Reynolds Number up to 708, which was still almost twice greater than the experimental results.⁷ By following the multiple scales approach, Cowley ⁸ showed that the disturbances can significantly grow over part of a cycle for asymptotically large Reynolds numbers. Lee¹ investigated the stability of the oscillatory planar Taylor-Culick flow using the multiple time scale method, and showed the possible effects of the turbulent transition due to the disturbance amplifications on combustion instability.

Up to now, studies on the stability analysis of the oscillatory Taylor-Culickflow are based on local methods.¹ The local non-parallel method can only describe the information of the certain local region, but is not capable to exactly and completely describe the non-parallel flow,⁹ such as Taylor-Culick flow. In this work, the biglobal stability of the oscillatory Taylor-Culick flow is investigated using the multiple time scale method.

Computational methodology

Governing equations

The linear non-dimensional continuity and momentum equations are adapted:

$\begin{array}{l} \nabla \cdot u^{'} = 0 \\ \frac{\partial u^{'}}{\partial t} + ({\bar{U}}_{B} \cdot \nabla) u^{'} + (u^{'} \cdot \nabla) {\bar{U}}_{B} + \nabla p^{'} = \frac{1}{R e_{i n j}} Δ u^{'} \end{array}$ $\begin{array}{l} \nabla \cdot u^{'} = 0 \\ \frac{\partial u^{'}}{\partial t} + ({\bar{U}}_{B} \cdot \nabla) u^{'} + (u^{'} \cdot \nabla) {\bar{U}}_{B} + \nabla p^{'} = \frac{1}{R e_{i n j}} Δ u^{'} \end{array}$ (1)

where basic flow ${\bar{U}}_{B} (r, t)$ ${\bar{U}}_{B} (r, t)$ are periodic, given as：

${\bar{U}}_{B} (r, t) = \bar{U} (r) + \hat{u} (r, t)$ ${\bar{U}}_{B} (r, t) = \bar{U} (r) + \hat{u} (r, t)$

where $\bar{U} (r)$ $\bar{U} (r)$ represent steady basic flow， $\hat{u} (r, t)$ $\hat{u} (r, t)$ acoustic velocity, r spatial coordinates, Re_inj is the Reynolds number of inject flow, and u’ is the perturbation velocity.

Multiple scales approach

The multiple scales approach, namely the fast time t and the slow time t₁ are related by $t_{1} = ε t$ $t_{1} = ε t$ with the small dimensionless expansion parameter, $ε$ $ε$ , characterizing the ratio of the time scales. Using the method of normal modes, the perturbation solutions is assumed to have the form as following

$(u^{'}, p^{'}) (r, t_{1}) = (u, p) (r, t_{1}) \exp (i ϑ)$ $(u^{'}, p^{'}) (r, t_{1}) = (u, p) (r, t_{1}) \exp (i ϑ)$ (2)

where $ϑ$ $ϑ$ is defined by

$ϑ = \frac{1}{ε} \int ω (t_{1}) d t_{1}$ $ϑ = \frac{1}{ε} \int ω (t_{1}) d t_{1}$

with

$\frac{\partial ϑ}{\partial t} = - ω (t_{1})$ $\frac{\partial ϑ}{\partial t} = - ω (t_{1})$

The chain rule transforms the temporal derivatives into

$\frac{\partial}{\partial t} = \frac{\partial}{\partial ϑ} \frac{\partial ϑ}{\partial t} + \frac{\partial}{\partial t_{1}} \frac{\partial t_{1}}{\partial t} = - ω (t_{1}) \frac{\partial}{\partial ϑ} + ε \frac{\partial}{\partial t_{1}}$ $\frac{\partial}{\partial t} = \frac{\partial}{\partial ϑ} \frac{\partial ϑ}{\partial t} + \frac{\partial}{\partial t_{1}} \frac{\partial t_{1}}{\partial t} = - ω (t_{1}) \frac{\partial}{\partial ϑ} + ε \frac{\partial}{\partial t_{1}}$

The disturbance amplitude $(u, p) (r, t_{1})$ $(u, p) (r, t_{1})$ are expanded in powers of $ε$ $ε$ as

$\begin{array}{l} u (r, t_{1}) = u_{0} (r, t_{1}) + ε u_{1} (r, t_{1}) + \dots, \\ p (r, t_{1}) = p_{0} (r, t_{1}) + ε p_{1} (r, t_{1}) + \dots . \end{array}$ $\begin{array}{l} u (r, t_{1}) = u_{0} (r, t_{1}) + ε u_{1} (r, t_{1}) + \dots, \\ p (r, t_{1}) = p_{0} (r, t_{1}) + ε p_{1} (r, t_{1}) + \dots . \end{array}$

Substituting the above expansion and Eq. (2) into Eq. (1) and collecting the terms with the same power of $ε$ $ε$ results in the zeroth order equations $(O (ε^{0}))$ $(O (ε^{0}))$

$\begin{array}{l} \nabla \cdot u_{0} = 0 \\ - ω u_{0} + ({\bar{U}}_{B} \cdot \nabla) u_{0} + (u_{0} \cdot \nabla) {\bar{U}}_{B} + \nabla p_{0} = \frac{1}{R e_{i n j}} Δ u_{0} \end{array}$ $\begin{array}{l} \nabla \cdot u_{0} = 0 \\ - ω u_{0} + ({\bar{U}}_{B} \cdot \nabla) u_{0} + (u_{0} \cdot \nabla) {\bar{U}}_{B} + \nabla p_{0} = \frac{1}{R e_{i n j}} Δ u_{0} \end{array}$ (3)

and the first order equations $(O (ε^{1}))$ $(O (ε^{1}))$

$\begin{array}{l} \nabla \cdot u_{1} = 0 \\ \frac{\partial u_{1}}{\partial t_{1}} - ω u_{1} + ({\bar{U}}_{B} \cdot \nabla) u_{1} + (u_{1} \cdot \nabla) {\bar{U}}_{B} + \nabla p_{1} = \frac{1}{R e_{i n j}} Δ u_{1} \end{array}$ $\begin{array}{l} \nabla \cdot u_{1} = 0 \\ \frac{\partial u_{1}}{\partial t_{1}} - ω u_{1} + ({\bar{U}}_{B} \cdot \nabla) u_{1} + (u_{1} \cdot \nabla) {\bar{U}}_{B} + \nabla p_{1} = \frac{1}{R e_{i n j}} Δ u_{1} \end{array}$

Defining ${\hat{u}}_{c}^{*}$ ${\hat{u}}_{c}^{*}$ as the acoustic velocity along the center line， $Π = {\hat{p}}^{*} / P^{*}$ $Π = {\hat{p}}^{*} / P^{*}$ the ratio of acoustic pressure and average pressure. ${\hat{p}}^{*}$ ${\hat{p}}^{*}$ and ${\hat{u}}_{c}^{*}$ ${\hat{u}}_{c}^{*}$ are related by linear momentum equation

${\hat{u}}_{c}^{*} = \frac{{\hat{p}}^{*}}{ρ^{*} c^{*}} = \frac{{\hat{p}}^{*}}{γ P^{*}} c^{*}$ ${\hat{u}}_{c}^{*} = \frac{{\hat{p}}^{*}}{ρ^{*} c^{*}} = \frac{{\hat{p}}^{*}}{γ P^{*}} c^{*}$ (4)

where sound velocity $c^{*} = \sqrt{γ P^{*} / ρ^{*}}$ $c^{*} = \sqrt{γ P^{*} / ρ^{*}}$ Similar to Stokes flow defining the boundary layer thickness as $δ^{*} = π V_{i n j} / Ω^{*}$ $δ^{*} = π V_{i n j} / Ω^{*}$ with $Ω^{*}$ $Ω^{*}$ the acoustic frequency. The expansion parameter $ε$ $ε$ in the present analysis is formally defined as¹

$ε = \frac{δ^{*} Ω^{*}}{{\hat{u}}_{c}^{*}} \approx O (\frac{M_{i n j}}{Π})$ $ε = \frac{δ^{*} Ω^{*}}{{\hat{u}}_{c}^{*}} \approx O (\frac{M_{i n j}}{Π})$

When $Π > > M_{i n j}$ $Π > > M_{i n j}$ ，the modulation is considered to be slow and the leading terms form the quasi-static problem.

Basic flow

Basic flows are the superposition of the steady flow and periodic acoutic field (Figure 1)

${\bar{U}}_{B} (r, t) = \bar{U} (r) + A \hat{u} (r, t)$ ${\bar{U}}_{B} (r, t) = \bar{U} (r) + A \hat{u} (r, t)$ (5)

where A represents the oscillation amplitude of acoustic velocity. $\bar{U} (r)$ $\bar{U} (r)$ Use the incompressible Taylor-Culick flow solutions obtained under the steady, axisymmetric, inviscid condition.¹⁰

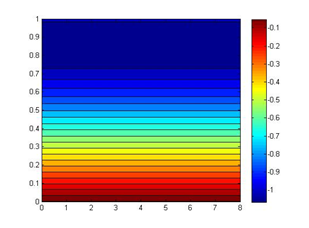
Figure 1 The contour of steady flow: axial velocity component $U_{z}$ $U_{z}$ (left) and radial velocity component $U_{r}$ $U_{r}$ (right).

$U_{r} = - \frac{1}{r} \sin (\frac{π r^{2}}{2}) U_{z} = π z \cos (\frac{π r^{2}}{2})$ $U_{r} = - \frac{1}{r} \sin (\frac{π r^{2}}{2}) U_{z} = π z \cos (\frac{π r^{2}}{2})$

$\hat{u} (r, t)$ $\hat{u} (r, t)$ can be obtained from the solutions of the unsteady flow providing by Flandro and Majdalani in a simulated solid propellant rocket.¹⁰

The oscillation amplitude of acoustic velocity A is defined as the ratio of acoustic velocity ${\hat{u}}_{c}^{*}$ ${\hat{u}}_{c}^{*}$ at the center line and injects velocity at the wall $V_{i n j}$ $V_{i n j}$

$A = \frac{{\hat{u}}_{c}^{*}}{V_{i n j}} = \frac{1}{γ M_{i n j}} \frac{{\hat{p}}^{*}}{P^{*}} = \frac{1}{γ M_{i n j}} Π$ $A = \frac{{\hat{u}}_{c}^{*}}{V_{i n j}} = \frac{1}{γ M_{i n j}} \frac{{\hat{p}}^{*}}{P^{*}} = \frac{1}{γ M_{i n j}} Π$ (6)

Supposing $Π = 0.018$ $Π = 0.018$ ， $M_{i n j} = 0.003$ $M_{i n j} = 0.003$ ， $γ = 1.2$ $γ = 1.2$ ，then A=5. Using Eq. (5), axial velocity component $U_{z}$ $U_{z}$ of the basic flows ${\bar{U}}_{B} (r, t)$ ${\bar{U}}_{B} (r, t)$ are plotted as following (Figure 2).

Figure 2 The contour of axial velocity component $U_{z}$ $U_{z}$ at four moments during a period.

Results and discussions

Eigen spectrum

A spectral collocation method¹¹ based on Chebyschev polynomials are used to numerically solve the eigenvalue problem (2). Figure 3 shows the eigenmodes at four moments during a period when $Π = 0.018$ $Π = 0.018$ ，namely A=5. The eigenvalues are discrete and exhibit one or two curve distribution which depends on time.

Figure 3 Eigenmodes at four moments during a period when $Π = 0.018$ $Π = 0.018$ .

The greatest growth rate is obtained at t=T/4 and corresponding eigenvectors are illustrated in Figure 4. The eigenvectors whose eigenvalues are in the same line in Figure 3 have similar distribution, with shorter wave length when increasing frequency. The eigenvectors of the greatest growth rate of the second line at t=3T/4 are showed in Figure 4B, where the axial velocity component $u_{z}$ $u_{z}$ shows one more wave in the radial direction when comparing to that of the first line.

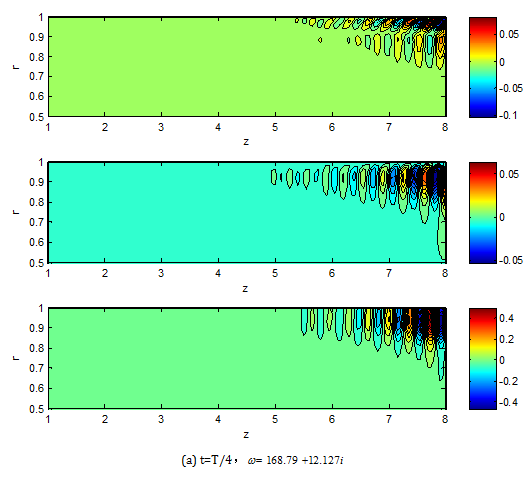
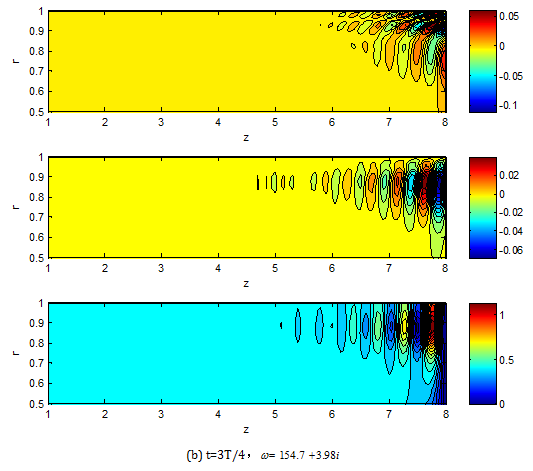
Figure 4 Eigenvector distribution, $u_{z}$ $u_{z}$ ( top)， $u_{r}$ $u_{r}$ (middle) and $p$ $p$ (down).

Effect of the acoustic oscillation frequency

The dimensionless chamber sound modes are given as

$Ω = Ω^{*} \frac{R}{V_{i n j}} = \frac{π c_{0}}{L} \frac{R}{V_{i n j}} = \frac{π}{L / R} \frac{1}{M_{i n j}}$ $Ω = Ω^{*} \frac{R}{V_{i n j}} = \frac{π c_{0}}{L} \frac{R}{V_{i n j}} = \frac{π}{L / R} \frac{1}{M_{i n j}}$

$Ω = 33 ， 52 ， 75$ $Ω = 33 ， 52 ， 75$ when aspect ratio L/R=32，20，14 with $M_{i n j} = 0.003$ $M_{i n j} = 0.003$ . Figure 5A shows the greatest growth rate at eight moments and average growth rate during a period of three acoustic frequencies with A=5. The growth rates at eight moments are different and the change range between them are larger at lower acoustic frequencies $Ω = 33 ， 52$ $Ω = 33 ， 52$ and decrease at higher acoustic frequencies $Ω = 75$ $Ω = 75$ . The straight line represents average growth rates during a period. It can be found that the larger growth rates correspond to higher acoustic frequencies, which are 11.6，10.3，8.0. The perturbation frequencies with the largest growth rate concentrated in the range from 100 to 250 (Figure 5B), which are much larger than the results for the steady basic flow.

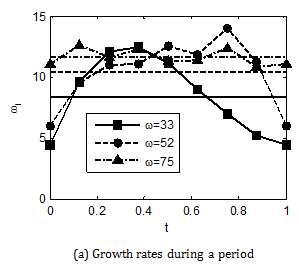
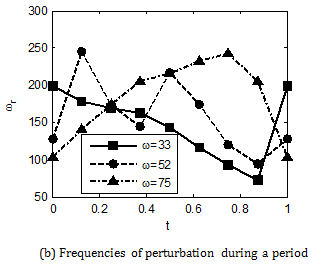
Figure 5 Stability results at three acoustic frequencies.

Effect of the acoustic oscillation amplitude

For given $Ω = 33$ $Ω = 33$ ，three different values of the acoustic oscillation amplitude A=1，5，10 are considered. From Figure 6, it is found that the larger growth rates correspond to higher acoustic oscillation amplitude, which is 11.3，8.4，0.9. The perturbation frequencies with the largest growth rate concentrated in the range from 100 to 200.

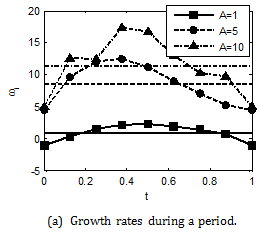
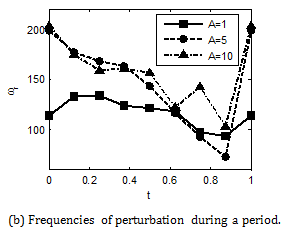
Figure 6 Stability results at three values of the acoustic oscillation amplitude.

Conclusions

In this work, the biglobal stability of the oscillatory Taylor-Culick flow has been investigated using the multiple time scale method. Basic flows are supposed to be the superposition of the steady flow and the periodic acoustic field, which is defined as the slow time and the fast time. It was established that when the dimensionless acoustic oscillation amplitude is much larger than the injecting Mach number, the modulation becomes slow and turns into a quasi-static problem.

A spectral collocation method based on the Chebyschev polynomials was used to numerically solve the eigenvalue problem. The eigenvalues are discrete and exhibit one or two curve distribution which depends on time. The larger growth rates were shown to correspond to higher acoustic frequencies, and the larger growth rates correspond to higher acoustic oscillation amplitude. The perturbation frequencies with the largest growth rate were found to be concentrated in the range from 100 to 250, which are much larger than that for the steady basic flow.^12-16