This paper describes a new approach for the design of optimum laminate stacking sequences. This technique uses an incremental procedure that combines implicit ternary decision trees with an informed search method based on an A-STAR algorithm capable of providing highly accurate and efficient solutions in terms of laminate computations. The method is especially suitable for thick composite laminate designs. Unlike other A-STAR implementations, in this case the main challenge lies in defining the heuristic function since the goal node is not known beforehand (blind search). To establish both the accuracy (minimum number of plies) and the efficiency of the new method, the technique was validated using a battery of Monte-Carlo simulations for the design of carbon fiber reinforced plastic plates subjected to a generic load case scenario and to some manufacturing constraints. This novel technology was then applied to the design of thick laminates, specifically in order to obtain the optimal solution (minimum laminate thickness) using the least number of optimization iterations.

Keywords: A-STAR algorithm, best first search, decision trees, discrete optimization, graph theory, minimum spanning tree, optimum laminate stacking sequence

ARSM, adaptative response surface method; BB, building block; BFS, breadth first search; CFRP, carbon fiber reinforced plastic; CLT, classical laminate theory; DOE, design of experiments; FBFS, fast best first search; GA, genetic algorithm; GSRM, global response surface method; NA, non available solution; RSM, response surface method; SF, safety factor

The use of composite laminate designs has become increasingly relevant in recent years owing to the demand for larger, lighter and stronger composite parts.¹ In some industries, like the wind energy sector, larger and thicker composite parts (i.e. blades) are required to build new multi-megawatt turbines. In this context, laminate optimization plays an important role in reducing costs and manufacturing competitive products. Yet, due to the high number of possible combinations, optimizing thick laminates is a challenge from an engineering point of view. In many cases, this optimization process consists of establishing the minimum number of plies in order to fulfill structural or manufacturing criteria.^1,2 This paper will refer to this kind of optimization as the structural sub-problem. It should be noted that quite often this problem is generally embedded within a wider multidisciplinary optimization issue. In some cases, a divide and conquer strategy is adopted for this kind of multidisciplinary problem, meaning that the initial problem is split into different sub-problems across different disciplines of physics. Given these circumstances, there is a clear need to create a ‘fast’ optimization algorithm able to provide high-quality solutions (as close to the global optimum as possible).

In the last decade the structural sub-problem has been resolved using several approaches. Among these, the response surface method (RSM) has attracted growing interest in recent years.³ This method uses design of experiments to (DOE) to approximate the unknown response surface, generating a surrogate model that is able to find the optimum. The surface response is approximated with a minimum number of experiments or simulations. Since the optimization search is cheap from a computational point of view, this technology matches the requirement to provide ‘fast’ optimization composite designs when a multidisciplinary optimization is needed. These RSM methods do not require any gradient evaluation (direct methods) and estimate the optimum with a minimum number of experiments or simulations.^4‒6 The quality of the final (approximate) solutions obtained with this technology depends on the type of surrogate models, the type of sampling to generate the initial surface points, as well as a number of other aspects.³

Evolutionary techniques constitute another approach capable of providing high quality designs, as shown in references.^7‒10 These evolutionary alternatives do not require any gradient computation and, in most cases, they are not sensitive to stacking at local optima. Genetic algorithms (GA) have proven effective in high-level optimum search performing and have been widely used to determine the optimum laminate stacking sequence for a laminate subjected to external forces and manufacturing constraints, see references.⁹ More recently^11,12 a new alternative breadth-first search (BFS) with implicit decision trees has emerged to provide and guarantee global optimum solutions for intermediate to moderate thick composite laminates using a similar or lower computational effort than genetic algorithms. One of the main drawbacks of both evolutionary techniques and BFS is that they usually involve a considerable number of computations when compared with the RSM alternatives.

In this context the algorithm presented in this paper has been developed to provide high-quality solutions with a minimum number of computations. This new method is built using an incremental decision tree in a similar way to the research produced by,^11,12 but it has a different expansion (search) scheme. It is a best-first search procedure guided by an A-STAR pattern (further details are given in the methodology section). Consequently, as will be demonstrated in the results section, the number of node expansions is significantly reduced and the algorithmic complexity becomes almost linear. This algorithm is especially suited to the design of thick laminates where the numbers of ply stacking combinations become huge. It should be noted that unlike in other A-STAR path finding implementations, this novel technique does not require the goal node tree position to be predetermined; this step will be circumvented with a parameter sweep, as described in the methodology section.

This paper is organized as follows: in section 2 the structural sub-problem is defined. Section 3, which forms the core and main contribution of this work, is devoted to describing the methodology. The algorithmic capacities in terms of quality and efficiency (number of laminate computations) are validated in the following section using a battery of optimization problems (Monte-Carlo simulations). The results are compared with the optimal solutions (quality) and with a fast greedy algorithm (efficiency). Finally, the novel technology is compared with some RSM^13,14 approaches for thick laminates, with the conclusion that the novel algorithm is able to fulfill the initial aim of providing fast high-quality solutions. The final section states the benefits of such a novel alternative and points to suggestions for future lines of research.

A simple rectangular composite plate is optimized by providing the laminate with the minimum number of plies, taking into account the following structural and manufacturing considerations. The relation between strains and load forces that a simple supported rectangular laminate plate has to withstand is given, according to classical laminate theory (CLT¹⁵):

$\left\{\begin{array}{c}{}_{{{\displaystyle N}}_x}\\ {{\displaystyle N}}_y\\ {{\displaystyle N}}_{xy}\\ {{\displaystyle M}}_x\\ {{\displaystyle M}}_y\\ {{\displaystyle M}}_{xy}\end{array}\right\}=\left[\begin{array}{cc}A& B\\ B& D\end{array}\right]\left\{\begin{array}{c}{{\displaystyle \epsilon }}_x^0\\ {{\displaystyle \epsilon }}_y^0\\ {{\displaystyle \gamma }}_{xy}^0\\ {{\displaystyle \kappa }}_x^0\\ {{\displaystyle \kappa }}_y^0\\ {{\displaystyle \kappa }}_{xy}^0\end{array}\right\}$    (1)

‘N’ relates to the external membrane load forces and ‘M’ is associated with the external moments. The ‘epsilon’ terms on the RHS (right hand side) represent normal and angular strains and the ‘kappa’ terms refer to plate curvatures. Finally, the sub-indices ‘x’ and ‘y’ refer to two orthogonal reference directions contained in the laminate plate mid-surface according to the scheme depicted in Figure 1.

These ABD matrices are determined according to the following Eq. (2).

$\begin{array}{l}{{\displaystyle A}}_{ij}={\displaystyle {\sum }_{k=1}^P{{\displaystyle \left({{\displaystyle Q}}_{ij}\right)}}_k\left({{\displaystyle Z}}_k-{{\displaystyle Z}}_{k-1}\right)}\\ {{\displaystyle B}}_{ij}=\frac{1}{2}{\displaystyle {\sum }_{k=1}^P{{\displaystyle \left({{\displaystyle Q}}_{ij}\right)}}_k\left(Z_k^2-Z_{k-1}^2\right)}\\ {{\displaystyle D}}_{ij}=\frac{1}{3}{\displaystyle {\sum }_{k=1}^P{{\displaystyle \left({{\displaystyle Q}}_{ij}\right)}}_k\left(Z_k^3-Z_{k-1}^3\right)}\end{array}$   (2)

These strains (transferring the result to the rest of the plies in the laminate according to CLT) are transformed into stresses by tensorial transformation and provide the safety factor (SF), which is calculated ply by ply as shown in Eq. (3).

$SF=mi{n}_k\left\{min\left\{\frac{{\sigma }_{1T}^{ua}}{{\sigma }_1^k},\frac{{\sigma }_{2T}^{ua}}{{\sigma }_2^k},\frac{{\sigma }_{1C}^{ua}}{{\sigma }_1^k},\frac{{\sigma }_{2C}^{ua}}{{\sigma }_2^k},\frac{S_{12}^{ua}}{\left|{\tau }_{12}^k\right|}\right\}\right\}$    (3)

Note that ‘k’ refers to the ‘k’ lamina. i=1, 2 and are the allowable stresses and are the principal material stresses for the lamina, being the maximum shear stress.

While there are many other structural integrity criteria, such as Puck or Tsai-Wu,¹⁶ to establish the SF we selected the maximum stress criterion (as indicated in Eq. (3)), as it is used extensively in laminate design for a vast number of applications.¹⁶ In this study, two types of carbon fiber reinforced plastic plies (CFRP) were used. Their mechanical properties and strengths are presented in the following Table 1.

All CLT evaluations were performed with a Python 2.7 script see.¹⁶ All the possible laminates were built using as building blocks (BBs) the following set of sub-laminates:

$\left\{0_2,{90}_2,{}_{-}{}^{+}45\right\}$

Only three BBs were used in this study and each BB was associated with a particular fiber orientation. In this paper the optimum laminate is restricted to being symmetrical and balanced; therefore the B matrix in Eq. (1) is a null matrix. However, this implies an important reduction in the variables design space due to the fact that half of the laminate has to be defined.

Figure 1 Schematic illustration of the ply stacking sequence.

Tree building

First, an incremental procedure was used to resolve the optimization problem with an implicit decision tree. Every node in the tree is a vector with three pieces of relevant information: the first is the laminate stacking sequence (possible solution to the problem); the second is a cost function for this particular node; and the third is the SF for the node. This decision tree is a ternary diagram showing the child node being generated from the parent node by adding one ply from the BB set $\left\{0_2,{90}_2,{}_{-}{}^{+}45\right\}$ to the previous laminate base (parent node). Thus every node is able to generate a maximum of three possible children, increasing the laminate thickness and the tree height by one unit per child generation. In this paper the tree height is referred also as a tree layer or tree depth. This tree building process is similar to that used in the references^11,12 but, as will be shown, with notable differences in the node pole information and the tree expansion. Implemented in Python 2.7, the tree starts with a root node, which expands by adding the siblings of the best node according to a particular rank score, see Figure 2. This best-first search expansion scheme is further described below. With this procedure, tree expansion and path finding occur simultaneously.

Best-first search tree expansion

Deterministic optimum path finding in a graph uses the following cost function to guide the search:

$f(n)=g(n)+h(n)$   (4)

Where ‘f(n)’ is the cost function for a node ‘n’ in the tree, ‘g(n)’ is the path cost, determined by the cost of going from the root to that node, and finally ‘h(n)’ is an estimation (heuristic) of the cost needed to reach the goal node (global optimum solution) from that particular node. Optimum solutions are guaranteed when the heuristic function ‘h(n)’ is underestimated.¹⁷ In some cases, such as depth-first, breadth-first or Dijkstra’s algorithms,¹⁷ ‘h(n)’ is equal to zero. In other cases, such as A-STAR and its variants,^18,19 ‘h(n)’ is not equal to zero, but rather the search algorithm takes advantage of the goal node information position to accelerate the optimization process to reach an optimal solution (underestimation) or sub-optimal solution (overestimation). In this study an A-STAR (best-first search) expansion scheme was chosen due to its proven optimal efficiency;²⁰ this means that no other algorithm using the same heuristic information expands fewer nodes than A-STAR. In this case, the goal node information was unknown (blind search), but this step was circumvented through a parameter sweep strategy as described in section 3.4.

In every iteration, the best-first search strategy uses two sets of nodes: the former is the non-expanded set in which there is a bunch of potential nodes (candidates to expand) where the tree could propagate (according to Eq. (4)), and the latter is a historic list of nodes that have been already used in the tree expansion. Nodes in the non-expanded set are classified and ranked according to Eq. (4). Therefore the tree expands with the ‘best’ node (minimum score according to Eq. (4)) in the non-expanded set, adding its children to the set. If there is a tie in the rank score between two or more nodes, a second node classification is established, taking into account the structural SF and choosing the safest node from the set of previously classified nodes according to Eq. (4). This best node, once evaluated, is moved from the non-process set to the historic list. Child nodes which violate any constraints (manufacturing constraint) are not included in this non-expanded set. The expansion stops for two possible reasons: if a feasible node is achieved (SF>1.0) or if the maximum number of tree expansions is generated.

Cost and heuristic function derivation

The BFS (breadth-first search) exploration technique is equivalent to a best-first search procedure, with the following cost function¹⁷

${{\displaystyle f}}_1(n)=g(n)=l_n$    (5)

In Eq. (5), ‘l(n)’ denotes an integer that defines the tree layer of a particular node. This cost function assumes that an edge in the tree costs exactly one unit and all edges have consequently the same cost. Since the heuristic is equal to zero according to Eq. (4), the minimum path in the tree provides the optimal solution. In addition,^11,12 has demonstrated that for the same problem as that discussed in this paper, a feasible solution (SF>1.0) using a BFS expansion is also the optimal solution. As shown in Figure 3, a stepwise trajectory was followed in a BFS. These trajectories are defined in this study by looking at the tree depth reached at the node where the tree expands at each iteration. Thus, a more vertical trajectory indicates that fewer nodes of the same tree layer were visited. In other words, in breadth-first searching the tree evolves horizontally with a particular tree layer and when all possible nodes in this layer (laminates with the same thickness) are generated, then the tree climbs to a higher layer.

Can this search process be enhanced by providing some verticality in the trajectories? The answer to this question is yes and this is accomplished using an A-STAR search scheme.^18,19 Such an algorithm can be implemented if the cost in Eq. (5) is forecast with a heuristic. Assuming we were able to predict that the goal node was located at a particular tree depth, then we would restrict the search and limit the tree depth to the optimal one. This can be mathematically formulated as follows:

${{\displaystyle f}}_2(n)=l_n+\left|\alpha -l_n\right|$    (6)

The second term on the RHS of Eq. (6) defines the heuristic function and is related to term ‘h(n)’ in Eq. (4). This heuristic is an absolute difference between a free parameter ‘α’ and the previous term, where ‘α’ is an integer that estimates the optimal number of layers that the tree needs to expand in order to generate a node that satisfies all constraints and a SF>1.0. Therefore the heuristic is an absolute value (which is never negative) measuring the distance between the current tree layer and the estimated optimum. It is straightforward to demonstrate that all nodes placed in a layer below ‘α’ have the same cost f₂(n) but we have to select just one single node from this set of nodes. In this context, it seems reasonable to expand the node with the highest SF. As a result, the tree expands more vertically than in breadth-first searching; owing to the correlation between SF and tree depth¹¹ the tree climbs until it reaches a layer equal to ‘α’.

It can be concluded that both the cost and the heuristic functions are derived from an improvement in the trajectories using a classical BFS algorithm, reducing the spanning in the tree. Two scenarios are possible depending on the heuristic:

1. If ‘α’ is overestimated, the tree expands vertically and stops the process when it finds a node with a SF>1.0, probably providing a sub-optimal solution.
2. If ‘α’ is underestimated or equal to the optimum number of tree layers, the tree expands vertically and when it reaches the layer equal to ‘α’ two possibilities can occur, first if SF>1 then the optimization process stops, providing an optimal solution, and secondly if SF<1, it bounces periodically between that layer and previous layers until it completes all possible nodes in those layers. It never goes to a node with a layer above ‘α’ because, according to Eq. (6), these nodes have a worse rank score (higher values). Finally when all possible nodes in these lower layers are generated, the tree starts to climb to a higher position above layer ‘α’, progressing in the same way as in a BFS search.

This process is graphically illustrated in Figure 4 using the same load case as Figure 3. From This Figure 4, it can be appreciate the change in trajectories following by the use of different alpha values. In summary, A-STAR is easily implemented by restricting the depth of the tree in the search and ranking the nodes as a function of their structural safeties. As the results section will show, this approach is extremely efficient, providing fast high-quality solutions, most of which match the global solution. Some important conclusions can be drawn from this cost and heuristic definition:

1. Both the cost and heuristic are simple functions. In addition, as the heuristic aims to guess the optimal laminate thickness (the optimal tree depth), it has a clear physical interpretation.
2. Since both the cost and heuristic function are determined exclusively from the tree layer, storing all the paths followed to get every node in the non-expanded set is not required because the cost is directly provided for each node using the node pole information. This reduces the space complexity (space memory needed) and makes the algorithm more efficient than most conventional A-STAR implementations that require node path information.

Algorithm implementation

As described previously, an estimation of ‘α’ is needed in order to implement the A-STAR algorithm.^18,19 This naturally gives rise to the question of how such a free parameter can be set. Since ‘α’ is an integer related to the maximum laminate thickness, one idea is to parallel sweep all its possible values instead of using just one single value. But we may justifiably question the expense of this approach from a computational point of view. Section 3.3 described how a low alpha (heuristic underestimation) resulted in a search equivalent to a BFS. In contrast, when the value was high (overestimation), the search complexity was almost linear. Therefore, if the number of tree expansions is restricted to being linear with the laminate thickness, then a fast algorithm (linear complexity) is implemented. The disadvantage of this approach is that the optimality guarantee is lost. That said, in the results section we will demonstrate through a Monte-Carlo simulation environment²¹ that the probability of reaching the optimal solution is high. As a consequence our novel algorithm is configured with these two parameters-alpha (specified in Eq. (6)) and the maximum number of tree expansions-as illustrated by the following simple pseudo code (Figure 5).

The solutions given by an increase in alpha will produce a growth in laminate thickness depending on the heuristic admissibility.¹⁷ We must remember that all possible solutions will not be obtained for every alpha in the sweep because of the restrictions to the number of tree expansions. Consequently, it is impossible to know if the best solution generated from this sweep is the optimal solution. In this pseudo code, the ‘alpha max’ parameter is fixed at 25 because a laminate solution of fewer than 100 plies is expected. Therefore the maximum number of iterations, limiting the number of tree expansions, should be of order 0(100). The viability of the parameters will be analyzed in the results section.

Algorithm efficiency

From the perspective of computational cost, the best decision tree that could be used to resolve the optimization problem is the one that reaches the goal node (optimal laminate) using a minimum number of expansions. In other words, this is the tree that only needs a single node (in the optimal path to the goal node) in every iteration, thus giving a number of expansions equal to:

$Numberoftreeexpansions=l_{optimal}$    (7)

This number increases slightly if using a best-first search strategy:

$Numberoftreeexpansions=NumberofBBs\ast l_{optimal}=3\ast l_{optimal}$    (8)

The best that can be achieved is of order & $O(l_{OPTIMAL})$ lsquo;’. A sub-optimal decision tree (greedy) approach subjected to this number of expansions (according to Eq. (7)) can be implemented easily using the following pseudo code (Figure 6).

This approach describes the ‘fast’ best-first search (FBFS) scheme that can be used to resolve the problem with minimum space and time requirements. However, as we will demonstrate in the results section, the quality of this greedy FBFS approach may be far removed from the optimal solution. Another relevant metric to rank the algorithmic efficiency is to measure the tree expansion by calculating the branching factor ‘b*’. This is defined according to¹⁷ as:

$N=1+b^{*}+{\left(b^{*}\right)}^2+{\left(b^{*}\right)}^3+\dots +{\left(b^{*}\right)}^l$     (9)

In Eq. (9) ‘N’ refers to the number of nodes expanded in the search by a particular tree whose depth is denoted by ‘l’. Notice that according to this expression the least effective branching factor is equal to ‘b*=3’, due to the fact that three building blocks are used $\left\{0_2,{90}_2,{}_{-}{}^{+}45\right\}$ ; in the best case it is close to ‘b*=1.00’.This factor is directly linked to the time and space complexity of the algorithm. Thus when ‘b*=1.00’ the algorithm complexity is linear; it is exponential in the rest of the cases and reaches a factor of ‘b*=3’ for a brute-force search procedure.

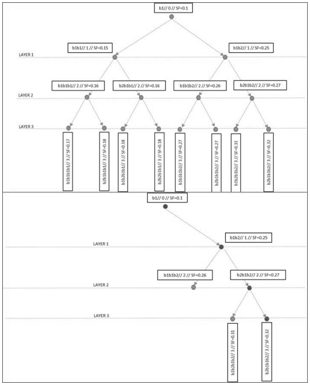
Figure 2 Example of tree. The upper graph shows an entire expanded tree formed with only two BBs (b1, b2) and three layers. The boxes indicate the node pole information. The lower picture depicts a best-first search expansion performed over the same tree (in this case the rank score is linked to the SF).

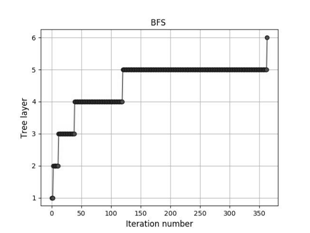
Figure 3 BFS trajectories followed for the tree in the membrane load case [NX=2000 New/mm, NY=2000 New/mm, NXY=0 New/mm] of the results section 4.1.

Figure 4 A-STAR expansions for different ‘α’ using the membrane load case [NX=2000 New/mm, NY=2000 New/mm, NXY=0 New/mm] described in section 4.1. The bottom figures are associated with an under-estimated alpha and the bottom ones to an over-estimation. The left figures indicate the tree layer progression and the right ones the SF progression during optimum search.

Monte-Carlo simulations

The free parameters of the algorithm were validated at this stage using a Monte-Carlo simulation environment. In addition, both the efficiency and quality of our novel algorithm were also checked. As described in sub-section 3.3, the free parameters of the algorithm were the maximum laminate thickness (‘alpha_max’ parameter) where the search takes place and the maximum number of tree expansions per search. These values were fixed at 25 and 500 respectively. The Monte-Carlo study²¹ assigned a uniform random distribution to each input variable (three membrane load components) and ran several simulations in order to obtain the density function of a particular response. Each response found the optimized laminate (as per the target described in section 2) for a particular load case. In other words, this Monte-Carlo study relates to an optimization search problem. A total of 496 membrane load cases (496 optimizations) were used, generated by a Latin Hypercube sampling procedure.²² The aim of each optimization problem was to minimize the number of plies (CFRP_a in Table 1) of a laminate subjected to a SF>1 and to the manufacturing constraints indicated in chapter 1. The structural SF is evaluated by classical laminate theory CLT as outlined in section 1. The histograms and statistics associated with these loads are given in the following scatter matrix plots (Figure 7).

As shown in the histograms,²³ the load components follow a uniform density distribution. We also notice that that there is no correlation between these load components. The responses obtained (best laminate designs) using the novel algorithm were compared with two other types of responses: those obtained from a BFS implicit decision tree (providing the optimal solutions according to^11,12) and those associated with the FBFS algorithm described in section 3.5. The objective of these comparisons is twofold: first to determine the quality of the results by checking deviations from the exact solutions (BFS implicit decision trees); and secondly to establish the number of computations and compare them with the pure greedy FBFS procedure in order to have an idea of the algorithmic speed. It has to be remarked that the term ‘exact’ is referred to the ‘real’ optimal solution and not to an approximation to such solution. Up to now, only a brute force approach or alternatively a digraph tree with a BFS exploration technique^11,12 can guarantee such a ‘real’ optimal solution. All laminate solutions (per load case) found by the three approaches (BFS, novel and FBFS) are listed in this repository.²⁴

The quality of the solutions is presented in Figure 8, measuring the difference (in number of plies) between the global optimum solutions found by the BFS approach and the other methods. It should be noted that for the novel method, a total of 25 processors were run in parallel according to the implementation procedure indicated in section 3.4. With this method, the final laminate design obtained per load case is given to the alpha linked to the minimum number of plies (according to the parallel search indicated in section 3.4).

In these graphs the laminate composite solution per load case and its deviation (in number of plies) from the reference solution are illustrated. The deviations are plotted both for the novel procedure or the FBFS. From this exercise, we can conclude that the novel algorithm matches the exact solutions in 98% of cases, which is a significant advance on the FBFS approach that is only able to match the exact solutions with a frequency of 70.3%. The novel approach demonstrates a high level of quality in laminate designs for a generalized membrane load case. Finally the efficiency of the novel algorithm was examined using as a metric the number of computations involved in each optimization search. First, the number of tree expansions required in each optimization was plotted against the number of laminate plies (Figure 9).

We can infer from Figure 9 that the algorithmic complexity is linear with the laminate thickness. The number of tree expansions is classified per the number of plies in each optimized design and are represented in this Figure 9 with a dot marker. The target line indicates a tree expansion that is linear with the ply thickness. Notice how the algorithm tree expansions are below the objective line in most of the load cases and are above in only seven load cases (1.41% of the total). In addition, the star markers in this Figure 9 indicate the minimum number of tree expansions provided by the FBFS procedure, giving an idea of the minimum number of computations that can be achieved. It should be pointed out that the novel algorithm is close to the FBFS (star marks), thus involving minimum tree spanning in most cases. Finally the tree branching factor ‘b*’ per laminate solution is shown in Figure 10. Notice from this Figure 10 how the branching factor is asymptotically stabilized with the laminate thickness to a low level close to 1.1 (close to linear branching), indicating an appropriate procedure to design thick laminates.

Comparison with other techniques

In order to establish any improvements provided by the new algorithm, it seems reasonable to compare its performance with other state-of-the-art optimizers, namely evolutionary and response surface methods, for load cases that involve thick laminate designs. For this purpose a total of six load cases were selected, corresponding to thick laminate designs close to 100 plies and including the effects of simultaneous membrane and bending (generic load case) loading. Notice that these thick laminates involves an exhaustive searching in the design space since there are a number of O (3¹⁰⁰ ) possibly ply configurations. These load cases are depicted in Table 2:

The main purpose of this section is to determine the efficiency and quality of the novel algorithm for the design of thick laminates, compared to commercial GA and RSM procedures. The GA and RSM methods were implemented with Hyperstudy.²⁵ In the GA implementation, each chromosome had a length of 25 genes and each gene was associated with a BB for a particular ply position. Since symmetrical and balanced laminates are imposed in the designs, the number of design variables (25) implies a maximum bound of 100 plies in the search. The genes were codified with integers belonging to the set (0, 1, 2, and 3). If a ‘0’ was selected for a particular gene, then there was no BB addition in this particular ply localization; the other integers were associated with the three possible BBs. The integer mapping codification is set out in the following Table 3.

The same discrete codification was applied to the global response surface method (GRSM) and to the adaptive response surface method (ARSM). Both techniques belong to the family of RSM methods briefly described in the introduction to this paper; further details can be found in the reference.³ The following Tables 4‒6, illustrate the optimization control parameters used for the three approaches.

Note that the parameters set out in Tables 4, 5 & 6 are the default parameters provided by the Hyperstudy software.²⁵ For the novel procedure, a total of 25 processors were used in parallel and the results reported with this new method correspond to the alpha (see Eq. (6) and the procedure described in Figure 6) with a minimum number of plies. The material parameters (CFRP_b) are presented in Table 1. The optimization exercise again involved obtaining the minimum number of plies that have a SF>1.0 and fulfill the manufacturing constraints (balanced and symmetrical laminates). For each load case, the SF was obtained using CLT as described in section 1.¹⁵ As opposed to the previous section, in this case the laminate ply stacking sequence has a clear relevance due to the effect of bending loads, rendering it a much more difficult problem to resolve (exponential complexity see^11,12). In order to score the results obtained using the different approaches, a ratio per load case is defined as follows:

$score=\left\{\frac{\left(\raisebox{1ex}{${{\displaystyle num\_evaluations}}^{-1}$}\!\left/ \!\raisebox{-1ex}{$num\_evaluation{s}_{best\_method}^{-1}$}\right.\right)}{\left(\raisebox{1ex}{$num\_plies$}\!\left/ \!\raisebox{-1ex}{$num\_plie{s}_{best\_method}$}\right.\right)}\right\}$    (10)

According to Eq. (10), for each load case, the highest scores are allocated to the approach which requires the least number of plies and the least number of laminate evaluations. In other words, the best score combines the two features targeted in this work into one single parameter. For each load case, the best method in the numerator of Eq. (10) is the one that requires the least number of evaluations, and the best method in the denominator is the one that generates the least number of plies. As a consequence the best score that can be obtained, according to the metric indicated in Eq. (10), is equal to the unity. It should be pointed out that for the GA, GRSM, ARSM approaches, the number of evaluations needed to achieve the optimum result on occasion exceeded the stop control criteria indicated in Tables 4, 5 & 6. These numbers of evaluations are averaged using ten runs per load case due to stochastic nature of such algorithms (GA, GRSM, ARSM)

The following table summarizes the results achieved for all the optimization approaches (Table 7).

The novel algorithm (A-STAR) returned the best scores in three load cases, followed by the ARSM, which had the highest scores in load cases 1 and 5. However, in load cases 2, 3 and 6, the ARSM was unable to find a feasible solution before it had reached the limit of 200 iterations according to Table 5. The GA achieved the minimum number of plies in most of the load cases but involved a high degree of computational effort, carrying a clear penalty as per Eq. (10). We may therefore conclude that the novel algorithm is robust and able to find a high-quality feasible solution for thick laminates with a minimum number of laminate evaluations.

Figure 7 Scatter matrix plots.

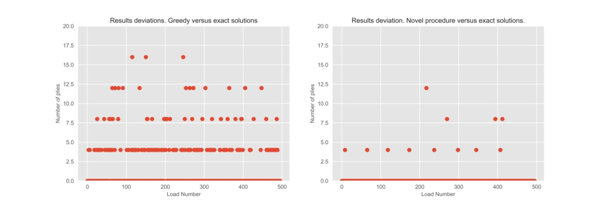
Figure 8 Number of ply deviations per load case. The graph on the left shows the results of the FBFS approach; the graph on the right gives the results obtained using novel algorithm.

Figure 9 Number of tree expansions performed with the novel algorithm in the Monte-Carlo study. The dot points represent the laminate solution obtained with the novel algorithm, the continuous line represents the linear results and the star marks denote the minimum number of evaluations performed by the FBFS algorithm. The results are represented per laminate thickness. The right-hand chart is a zoomed-in view of the left-hand one but with the outliers (three simulations with more than 100 evaluations) removed.

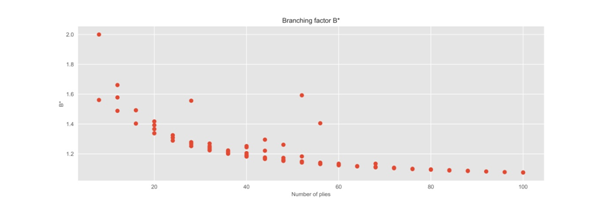
Figure 10 Tree branching factor ‘b*’ for the novel algorithm in the Monte-Carlo set of simulations. The ‘b*’ values are represented per laminate thickness.

This study has described a novel search procedure, based on implicit decision trees and A-STAR techniques,^18,19 for the design of an optimum laminate stacking sequence. The procedure is able to find ‘fast’ optimal or sub-optimal solutions with a slight grade deviation from the exact solutions, but where the probability of finding the exact solution is high. Further advantages of this new optimization technique can be summarized as follows:

1. The number of laminate evaluations has the same order as the number of plies. This has a high degree of relevance and a direct application to thick laminate designs.
2. Only two degrees of freedom, both with a clear physical meaning, are required. The first is the maximum laminate thickness (it defines the alpha parameter, see Eq. (6)) and the second is the maximum number of tree expansions.
3. There is no need to define stop criteria as with other optimization algorithms.
4. There is no need to establish an initialization procedure, i.e. define an initial population in the case of GA or an initial sampling in the RSM.

The technique is based on an incremental implicit tree approach^11,12 but unlike the BFS approaches reported in previous research¹¹ a minimum spanning tree is combined with a best-first search scheme and supported by a heuristic function. This procedure is inspired by an A-STAR path finding scheme but, as opposed to conventional A-STAR techniques,^18,19 the goal node is not known beforehand. In this paper the laminate problem described in section 2 is resolved for a high number of membrane load cases (Monte-Carlo simulation environment), using three approaches: the novel algorithm, a BFS solver and a FBFS approach in order to establish the speed (in terms of node computations) and the quality (in terms of deviation with respect to the exact solutions) of the first approach (i.e. the novel algorithm). These solutions are given in the URL repository,²⁴ which provides a database that could be used to check the capabilities of future algorithms. Indeed, this database is another contribution of this work and provides a framework to calibrate any new optimization algorithm. In this present case, the novel algorithm was able to find the optimal solutions with a success probability above 98% and with a number of evaluations close to the maximum bound established by the FBFS approach. Finally, the results section showed how the novel procedure produces laminate designs with a thickness (quality) close to GA¹³ but using lower computational ‘effort’, which is similar to or better than the RSM approaches.¹⁴

It should be mentioned that this novel procedure complements the implicit tree technology for the design of composites developed by Sanz-Corretge in his previous research^11,12 and offers new applications in multidisciplinary optimizations where fast algorithms are needed. Unlike the optimization algorithms developed in,^11,12 the new technique is mono-objective and is restricted to BBs of the same cost. Where BBs of different costs are studied, either the cost or heuristic functions should be modified in the Eq. (6). This modification does not follow a straight derivation and further research should be carried out. One possibility would be to determine a homogenization procedure, which would substitute the original set of BBs of different costs with an equivalent set of BBs of equal cost, and impose a ply stacking sequence as an artificial manufacturing constraint. For instance, for simplicity’s sake, let us consider that there are two initial BBs: one costs one unit and the other costs three units. One possibility would be to transform these BBs into two new ones: the one that initially cost one unit would remain unchanged and the one costing three units would be sliced in artificial plies of one third thickness (assuming that the cost is proportional to the thickness). In this case it would be necessary to impose the manufacturing constraint of stacking the artificial new plies (associated with the modified BB) as three multiples. Note that the addition of a new manufacturing constraint in implicit tree technology^11,12 speeds the search and aids the optimization process.

As a future line of research, the initial study could be implemented and embedded in a more complex multidisciplinary optimization (i.e. in airfoil optimization), where the benefits of the speed and accuracy of the new algorithm can contribute to obtaining fast designs.

None.

The author declares that there is no conflict of interest.

1. Eckold G. Design and manufacture of composite structures. UK: Woodhead Publishing; 1994. 400 p.
2. Bailie JA, Ley RP, Pasricha A. A summary and review of composite laminate design guidelines. NASA Contract NAS1-19347; 1997.
3. Kihuri André I, Mukhopadhyay S. Response surface methodology. Computational Statistics. 2010;2(2):1–15.
4. Fu Xinwei, Ricci Sergio, Bisagni Chiara. Multi-scale analysis and optimization of three-dimensional woven composite structures combining response surface method and genetic algorithms. CEAS Aeronautical Journal. 2017;8(1):129–141.
5. Abbas V. Optimization of composite pressure vessels with metal liner by adaptive response surface method. Journal of Mechanical Science and Technology. 2011;25(11):2811–2816.
6. Venter G, Haftka RT. Using response surface approximations in fuzzy set based design optimization. Structural and Multidisciplinary Optimization. 1999;18(4):218–227.
7. Hee Keun Cho. Maximizing structure performances of a sandwich panel with hybrid composite skins using particle swarm optimization algorithm. Journal of Mechanical Science and Technology. 2009;23(12):3143–3152.
8. Kong YM, Choi SH, Yang BS, et al. Development of integrated evolutionary optimization algorithm and its application to optimum design of ship structures. Journal of Mechanical Science and Technology. 2008;22(7):1313–1322.
9. Lopez RH, Luersen MA, Cursi ES. Optimization of laminated composites considering different failure criteria. Composites Part B: Engineering. 2009;40(8):731–740.
10. Todoroki A, Haftka RT. Stacking sequence optimization by a genetic algorithm with a new recessive gene like repair strategy. Composites Part B: Engineering. 1998;29(3):277–285.
11. Sanz-Corretge Javier. A procedure to Design Optimum Composite Plates Using Implicit Decision Trees. Structural and Multidisciplinary Optimization. 2017. 56(5):1169–1183.
12. Sanz-Corretge Javier, Echeverría Mikel. A novel technique for the design of hybrid composite laminates based on dynamic programming and dynamic tree trimming. Structural and Multidisciplinary Optimization. 2018;57(4):1507–1521.
13. Goldberg DE. Genetic algorithms in search, optimization and machine learning. Boston: Addison Wesley Longman. Inc; 1989.
14. Python 2.7.11 documentation. URL: https://docs.python.org/2.7/
15. Kollár LP, Springer GS. Mechanics of composite structures. UK: Cambridge University Press; 2003. 500p.
16. Jones RM. Mechanics of composite materials. 2nd edn. Virginia: Taylor & Francis (Materials Science & Engineering Series); 1999. 270 p.
17. Rusell SJ, Norvig P. Artificial intelligence: a modern approach. New York: Pearson; 2016. 1152 p.
18. Hansen Eric A, Rong Zhou. Anytime Heuristic Search. J Artif Intell Res. 2007;28:267–297.
19. Zeng W, Church RL. Finding shortest paths on real road networks: the case for A*. International Journal of Geographical Information Science. 2009;23(4):531–543.
20. Dechter Rina, Judea Pearl. Generalized best-first search strategies and the optimality of A*. Journal of the ACM. 1985;32(3):505–536.
21. Rubinstein Reuven Y,‎ Kroese Dirk P. Simulation and the Monte Carlo Method. USA: Wiley Series in Probability and Statistics; 2016. 372 p.
22. Tang B. Orthogonal Array-Based Latin Hypercubes. Journal of the American Statistical Association. 1993;88(424):1392–1397.
23. Hunter JD. Matplotlib: A 2D graphics environment. Computing In Science & Engineering. 2012;9(3):90–95.
24. URL:https://www.dropbox.com/s/8s3nymuzgode4hm/repository.zip?dl=0
25. Hyper Study. Michigan: Altair Engineering, Inc.; 2017. 137 p.