Beneficiation of regolith to concentrate the high-density ore fraction from the gangue can be accomplished through momentum transfer methods, such as ballistic deflection or cyclonic separation.This study explores the extraction of actinide-bearing minerals from lunar regolith based on the difference in apparent density between thorium-bearing minerals (e.g. ThO₂ρ=10) from silicates (e.g. SiO₂ρ=2.65).Thorium content in lunar regolith ranges from single-digit parts per million (ppm) to as high as 60 ppm.Concentrating thorium-bearing minerals is a required first step in the preparation of fission fuels for a nuclear reactor in which all of the radioactive operations are performed 380,000 km from the Earth’s biosphere. After comparison with ballistic deflection, cyclone separation with a non-volatile fluid carrier was chosen for further study.With sieving to separate particles by size, such a hydrocyclone can be used to efficiently separate the dense fraction from the lighter minerals.Design equations were used to fabricate an at-scale apparatus using water, iron particles, and glass beads as simulants.Results show the ability to effect a 2 to 5.4 % increase in dense fraction concentration each pass, such that 95% concentration requires between 50 and 100 passes, or a cascade of this many apparatuses.The selection of a suitable fluid for safe and low-mass transport to the Moon is part of a techno-economic analysis of the cost and infrastructure needed to produce highly-purified thorium minerals on the lunar surface.

Keywords:thorium, sorting, beneficiation, ISRU, Moon, fission

Beneficiation of regolith is more challenging in space than on earth because rich ore bodies are rare.The local environment on, for example, Earth’s Moon, is further challenged by the low gravity, lack of water and air, and the mobility, radiation, and temperature extremes faced by either a human or a robotic operator.In-situ resource utilization (ISRU) is the general term for extracting and using materials and energy already found in space.An important aspiration for ISRU activities is the ability to produce abundant baseload electricity.The ideal lunar power source is a nuclear fission reactor.However, because of terrestrial concerns over risk, the launching of radioactive material is controversial.An alternative exists.

Thorium on the surface of the Moon offers a powerful source of nuclear energy and is found in abundant concentrations across wide expanses of the lunar near-side and south pole. On the lunar surface, thorium is naturally occurring as thorium dioxide (ThO₂) that needs to be processed, sorted, and separated from lunar regolith and refined into uranium-233 which is a fissile byproduct useful as nuclear fuel.

The present study was carried out to determine the viability of cyclone separators (centrifugal classifiers) in successfully separating, sorting, and concentrating extracted actinide-bearing minerals from lunar regolith based on the difference in apparent density. Particularly, this study focused on the use of hydrocyclones to classify particles of different densities. The effects of variables such as input mass ratio of dense particles and cyclone axis angle were investigated. Steel (7.5g/cc) and glass beads (2.4g/cc) were used to simulate high and low-density particles respectively. The separation products of the experiments with the most promising results were analyzed and then compared in terms of increase in high-density ore concentration. Lastly, due to wide variations in operating conditions on the moon, a suitable liquid is needed as the working fluid.While water is in this study for demonstration, other suitable fluids, proposed for safe and low-mass transport, are recommended for use of the moon.

Hydrocyclones are continuously operating centrifugal classifiers that use differences in drag and inertial forces to separate particles based on size, shape, and density. A hydrocyclone works by creating a vortex of water mixed with solids within a cylindrical vessel that tapers into a cone. The vortex causes centrifugal effects on the solids, inducing the heavier ones to disengage from the flow and remain along the interior walls, while light particles migrate towards the center of the vortex due to drag forces. Simultaneously, the taper of the cone causes the vortex to reverse direction, allowing most of the liquid to exit from a top port called the vortex finder, carrying with it the lighter particles. Figure 1 below illustrates the flow in a hydrocyclone.¹

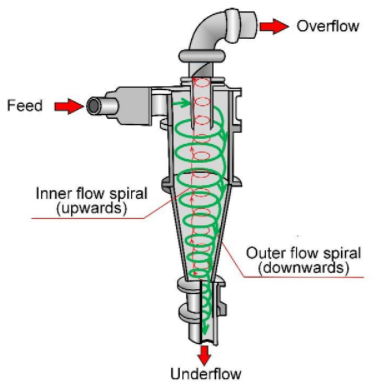
Figure 1 Visualization of a hydrocyclone.¹³

Cyclones in general offer the benefits of a continuous flow, separation of similarly sized particles by density and take a small footprint compared to other sorting devices such as gravity sorters.

Additionally, hydrocyclones can operate under lunar gravity. In fact, Bradley³ explains that “the cyclone is a piece of equipment which utilizes fluid pressure energy to create rotational fluid motion.” Gravity has a negligible effect on hydrocyclone performance. It is primarily by viscosity, drag forces and inertial effects or centrifugal forces that the separation effects occur. It is only for cyclones of large diameters and operating at low pressure that “the position of their axis,” hence gravity, matters.³

While there is an extensive amount of computational fluid dynamics studies, few analytical studies have investigated density separation in a hydrocyclone.⁴ Cyclone modeling is a complex undertaking. As indicated by Sovechles,¹ empirical models for hydrocyclones “are not based on any specific theory of hydrocyclone operation and are derived by fitting models to experimental data.” Despite this lack of defining theories, key governing equations for fluid motion and particles interactions are the mass (1) and momentum (2) balance equations:

$\frac{\delta \rho }{\delta t}+\frac{\delta }{\delta x_i}\left(\rho {\overline{u}}_i\right)=0$   (1)

$\frac{\delta }{\delta t}\left(\rho ({\overline{u}}_i)\right)+\frac{\delta }{\delta x_i}\left(\rho \left({\overline{u}}_i\right)\left({\overline{u}}_j\right)\right)=-\frac{\delta \overline{P}}{\delta x_i}+\frac{\delta }{\delta x_i}\left[\mu \left(\frac{\delta {\sigma }_{ij}}{\delta x_i}\right)\right]-\frac{\delta {\tau }_{ij}}{\delta x_i}$   (2)

The main forces on particles include the centrifugal force due to the tangential motion, the centripetal buoyancy force due to the radial pressure gradient, and the centripetal drag force due to the viscosity of the liquid. They are governed by the Navier-Stokes equation, with components defined, respectively, as:⁵

$F_C=\frac{\pi d_s{\rho }_s{\omega }^{2}r}{6}{F}_B=\frac{\pi d_s{\rho }_f{\omega }^{2}r}{6}{F}_D=\frac{\pi C_D{d}_s{\rho }_f{\upsilon }^{2}r}{8}$   (3)

Further mathematical models on particle-fluid interactions can be found elsewhere.⁶ Relevant models in software packages such as ANSYS include the Large Eddy Simulation (LES) to model the hydrocyclone turbulence, Discrete Phase Model (DPM) to predict particle separation, the Reynolds Stress Model (RSM) to predict the velocity and pressure distribution.⁵

Design process

The key design requirements for the prototype experimental density sorting device included the following considerations:

Density separation: To separate high-density particles from low-density ores with minimal noise from particle sizing effects. A target for less than 200 cycles to 99% purity was set for the sorter.

Semi-continuous process: To maximize the duration the process can run with minimal human interaction.

Visible operation: Clear materials and observable process. The opacity of slurries or cyclone materials can prevent proper assessment of the flow.

Iterable and adaptable: Flexible geometrical & operation changes

Empirical performance charts are typically used as design standards for hydrocyclones. Cyclones are generally classified by their diameters. It is an industry standard for manufacturers to produce a finite range of hydrocyclone designs with progressive diameters.These are characterized by empirical charts on separation versus flow rate for a given hydrocyclone design, with various “aperture sizes (inlet, overflow and underflow) through the use of interchangeable parts” for various cyclone operations.¹From knowledge of standard diameters, capacities, pressure drops, and cut sizes, various cyclones can be designed to suit a wide range of operations.

Bradley³ adapted performance data for a Heyl and Patterson hydrocyclone, a widely used type of hydrocyclone, as seen in Table 1 below.

Separation mechanism apparatus

A density separator setup was constructed for this study as depicted in Figure 4, consisting of a model CV06 mini cyclone separator (Figure 2-an air cyclone separator that was retrofitted into a hydrocyclone through the application of water-resistant sealants and a gasket), a water drum (liquid reservoir), an autotransformer (to adjust power to the pumps), a centrifugalpump (the primary pump for pumping liquid into the hydrocyclone from the reservoir), a diaphragm pump (sump pump responsible for returning spent fluids to the reservoir), two collection buckets (one overflow collection bucket and one underflow collection bucket) and a feed insert tube. Quick-Grip® clamps were used as gates to control the flow connection between the feed tube and the hydrocyclone. A custom-made table was designed to house the setup. The circuit was operated at a fixed flow rate of 1.24 l/s (1177 GPH).

Materials

Round glass beads having diameters of 0.25-0.4mm (2.4g/cc) were used to simulate the bulk of lunar regolith, and stainless steel balls of 0.25-0.4mm diameter (7.5g/cc) were used to simulate actinide minerals, and the working fluid was water. This relatively narrow size range provides greater clarity on density sorting relative to size sorting.

Figure 2 Model CV06 Mini Cyclone (www.clearvuecyclones.com).

Figure 3 Fluid and material flow diagram showing a funnel shape hopper instead of the slurry bulb and clamp used herein.

Figure 4 Experimental apparatus in tilted configuration, taken from 1.7 meters elevation (slurry bulb not shown at ‘INSERT’ point).

Post-separation mechanism (filtration)

A separate filtration system was utilized to ensure that the separation process using the hydrocyclone could be kept continuous eliminating the need to halt the system for particle filtration purposes. The filtration system consists of coffee filters, sieves of mesh size 40, 50 and 60 (425, 300, and 212 microns, respectively), and a bar magnet. The ideal outcome would be for all of the high-density metal particles to be caught in the underflow while all of the low-density glass particles would be collected in the overflow. However, given the number of factors that affects cyclone separation efficiency; there were always mixtures in both the overflow and underflow. After the particles from both sides were recovered and dried separately, the bar magnet was used to separate the steel particles from the glass particles so that the particles could be weighed independently and recorded.

Experiment setup

Figure 4 shows the experimental apparatus, which is tilted away from the point-of-view at an angle of 20 degrees. Water was drawn from the source reservoir and directed through a lateral tube to the tangential inlet port of the hydrocyclone.A T-junction along the lateral tube allowed introduction of particles to the water flow.Particles were mixed with water to form slurry, which was then introduced to a flexible plastic bulb.The bulb was attached to the T-junction via a flexible section of those whose cross-section was controlled by the Quick-Grip® clamps. To start an experimental run, the clamps were released, and the slurry ran downward (the rate is easily adapted to lunar gravity) allowing the particles to mix with the primary fluid flow along the lateral tube.

During experimental runs, the primary fluid flow was established first, so that the air core inner vortex initially created has time to be fully-filled with water.In a vacuum environment this would happen even faster.In continuous operation this step would only be needed at cold starts.Once the flow has stabilized the clamp is released and the slurry of particles and water drain into the lateral tube.The particles become entrained with the primary flow and are injected into the hydrocyclone tangential inlet port, and begin to swirl, as shown in figure 1.

The mixture of particles is then becomes separated into the overflow and the underflow. The particle collection buckets were tilted at an angle to allow excess particle-free fluid to flow into a fluid collection container.From there, the fluid is pumped back to the source reservoir to be recycled for continuous operation.These buckets were sized such that the particles settled in front of the weir, and must be taller for operations in lunar gravity (0.166g), where settling is slower.

Due to the experimental constraints of having the test results independent from one another, the operation of the system was halted once the mixture of particles had gone through the hydrocyclone. This also allowed for the monitoring of clogged particles’ presence in the apparatus so that they can be removed to ensure subsequent experiments were carried out with similar and consistent parameters(Figure 3-6).

Test conditions

A key change from the original CV06 Mini Cyclone was the addition of a 3D-printed underflow spigot/apex nozzle made of PLA (see Figure 7). This changed the underflow opening from the original diameter of 2.25 inches (designed for air) to 0.25 inches (adapted for water).As was observed during the experiment and from literature that “limiting the fraction of water in the underflow increases the separation efficiency”.¹Sovechles also indicated that “this restriction increases both the particle density and the radial velocity around the apex region,” leading to more water and low-density materials reporting to the overflow while high-density ones report to the underflow.

Figure 5 Schematic representation of the experimental setup.

Figure 6 Total of 270 g of particles, consisting of glass (white) and steel (dark gray), before mixing and testing.

Figure 7 Underflow apex nozzle design: 0.25-inch aperture diameter.

It has been indicated that the shape of the underflow spray influences the performance of a hydrocyclone.⁷ The change to a 0.25-in diameter underflow (Figure 8) also led to a discharge visually shaped between a roping discharge and a spray (figure 9 left).The 0.25-inch diameter was submerged underwater to eliminate the air core, and reduce underflow particle mixing (figure 9 right).This reasonably simulates the airless conditions on the Moon. Further details on methods are presented in the Appendix.

Figure 8 Left: Upper part of the cyclone in operation (No air core is observed). Right: Conical part of the cyclone with a nozzle reducer at the underflow aperture.

Figure 9 Left: Outlet spray pattern (bottom) with custom apex aperture underflow. Right: Submerged apex, and weir overflow.

Separation and concentration results

After running a test, there are three outcomes from the input of steel and glass particles:

1. Recovery in the underflow
2. Rejection via the overflow
3. Material loss within the apparatus

The hypothesis to be tested is that proportionately more steel than glass will be recovered in the underflow, and that the rejected overflow will be deficient in high-density particles.An ideal design will have no dead spaces in which particles of either density can become fully disengaged through the flow.With the extant apparatus, some amount of loss was experienced in each run.Lost material was removed from results, and assumed to be all high-density particles, so that all readings are reported in the least favorable way possible.

Figure 10 shows the particles recovered in the underflow from the original 270g of figure 7. Visually, the loss of glass particles in the underflow is readily appreciated.In terms of solids concentration, this indicates an increase in steel concentration at the underflow, or a higher ratio of steel mass to total underflow mass.

Figure 10 Recovered, dried, and magnetically separated underflow particles from a test run using the material of Fig 6.

Figure 11 shows the rejected overflow material, which has been dried and then separated magnetically to separately weigh each fraction.Visually, the amount of glass (light brown) is much more than the amount of steel (dark).Of course, mass readings have given a more accurate indication, as presented below.Variable loss of material inside the cyclone became a source of experimental error, per the assumption made that only high-density particles were lost in this way.

Figure 11 Steel (black) and glass (light brown) across three independent tests. Top row: The two on the left are from overflow and the two on the right are lost from that test. Bottom row: Two on the left and two on the right are from the overflow of two different tests.

Measured results for overflow and underflow are reported in input ratio of high-density to total input mass, and the increase in recovered underflow concentration of high-density particles after one cycle, as a function of hydrocylone tilt angle.Separation enrichment as a percentage is reported in the last column, and ranges between 1.0 and 5.4 percent concentration per cycle(Table 2).

Not reported are many of the early trials, which were not usable due to issues with measurement and learning to operate the system. An immediate observation from Table 2 is that across various test conditions, relatively similar concentration improvements were observed. Within the range reported, most results lie within the range of 2 to 3 percent separation enrichment.

Graphs of each variable versus the separation (steel concentration increase) are shown below. As multiple factors were changed between trials, these graphs provide only average behavior, with other variables being confounded behind a linear trend line.Goodness-of-fit metric R² is low due to variability, but also due to the relative insensitivity of performance to initial material mix ratio.This is a favorablefinding when considering multiple sequential separation stages(Figures 12-14).

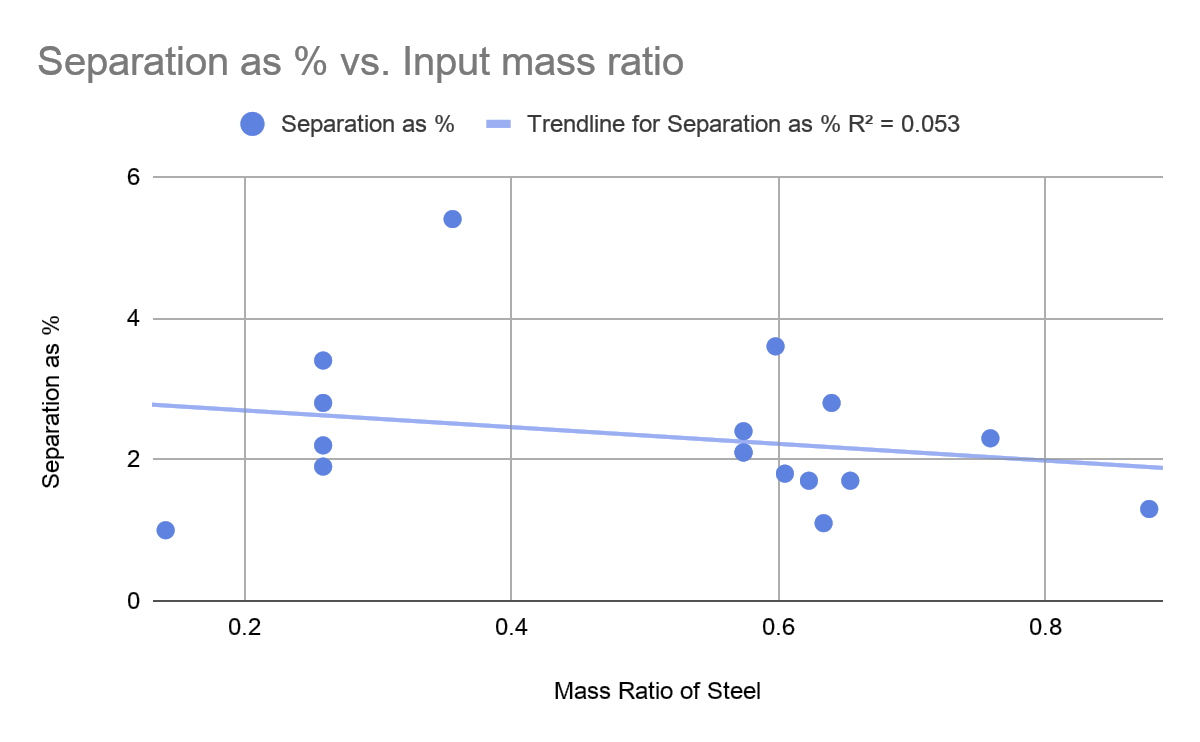
Figure 12 Separation enrichment of high-density particles (steel) as a function of the input mass ratio.

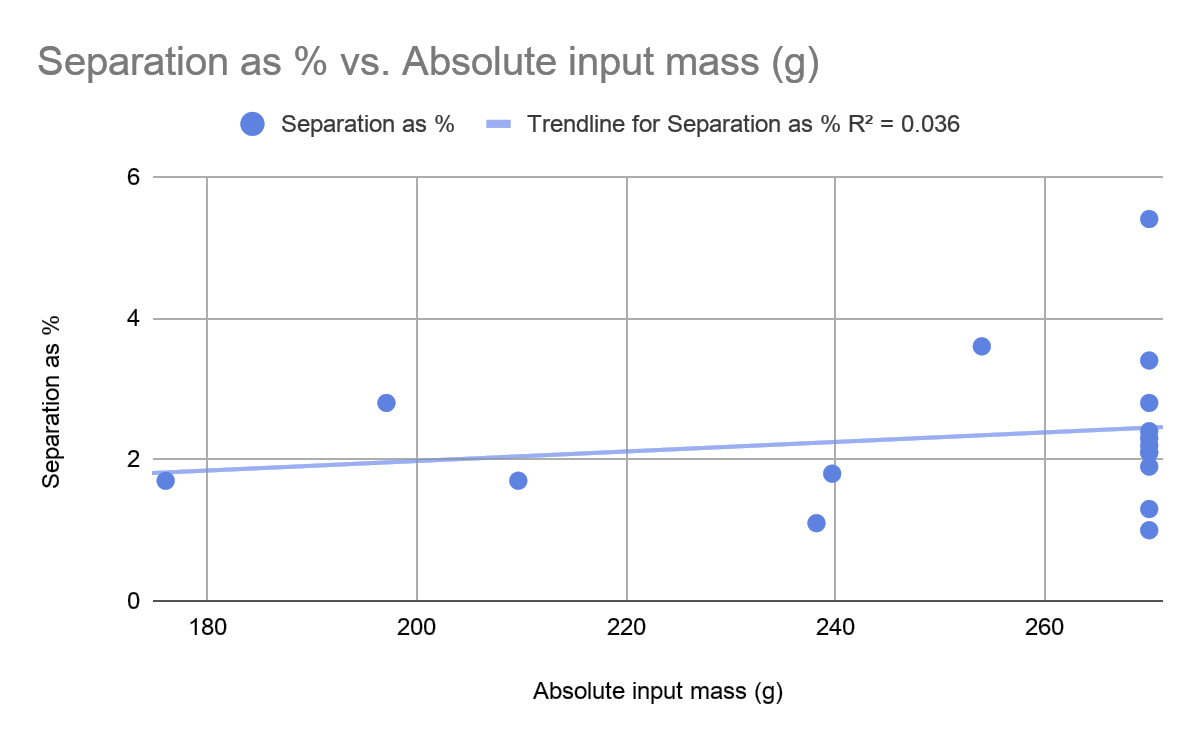
Figure 13 Separation enrichment of high-density particles as a function of the absolute total mass of input material.

Figure 14 Separation enrichment of high-density particles versus the tilt angle of the apparatus.

Figures 13 & 14 show insensitivity to starting load mass and to the tilt angle of the apparatus.The first is favorable becausethe process operates within at least this range of input flow rates without appreciable influence on the outcome.The second is favorable because it indicates insensitivity to gravity, as was expected based on review of the literature.

Effects of particles steel input mass ratio on high-density particles concentrations

Figure 15 shows composite data on enrichment versus input mass ratio of high-density particles. Results from repeated trials were averaged to reduce scatter.

The rightmost point on the plot of figure 15 was calculated because, obviously, if only high-density steel is input, than the underflow will be 100% steel, and the enrichment will be identically zero.The other three points, covering a 3:1 range of concentration, again show the relative insensitivity of separation enrichment with the mix ratio of high- and low-density particles.The rise towards smaller input mix ratios is encouraging because of the low initial concentration of actinide-bearing minerals in the lunar regolith.This result increases confidence in predicting the outcome of successive or repeated passed through the hydrocyclone.

Figure 15 Input mass ratio versus separation percent in 27 degree tests with 270g total input.

This would seem consistent with expectations of hydrocyclone operation, as when a larger proportion of the light material (glass in the experiments) is present, it is more likely for the reversed vortex to capture it and for it to report to the overflow. Further, existing research indicates that heavy particles are much easier to control than lighter ones,⁵ which is consistent with this trend: the primary factor changing between trials can be assumed to be the number of light particles (glass) being removed through the overflow, which is more volatile than the number of heavy particles (steel) falling to the underflow.

Estimation of the number of cycles to purity

One goal of this research was to estimate the required number of cycles to achieve relatively pure thoria in the practical version. There are several variables that still need to be tested, especially the behavior of the hydrocyclone starting from very low mass concentrations of the heavy material and with smaller particle sizes as would be prevalent in situ. However, some amount of rough estimation is possible.Given the weak dependence of separation enrichment with respect to most process variables, a simple relationship between the purity C and thenumber of cycles n can of enrichment fraction x be expressed as:

$C=.99999-{(1-x)}^n$   (4)

This assumes the initial actinide concentration is approximately 10ppm.With the average concentration results found herein of about 0.025, and a target concentration of 95% pure actinide mineral (eg. thoria), the number of cycles required is 120.

Each sample run, after reaching steady state, required between 22 and 30 seconds before the particles were no longer visible inside the clear hydrocyclone body.Using 60 seconds as a cycle time, including time to return the underflow to the inlet feed, a 0.25kg batch can be purified in 2.0 hours.This results in a process flow rate of 1.25mg of actinide material per hour of operation.To achieve a 15kg mass of material then requires 12,000 hours, or 50 earth-days of duration.If this work is performed using solar power which only runs 50% of the time, the duration extends to 100 days of lunar operations.This quantity of thoria, when transmuted to uranium, can power a 2MWe fission reactor for over six years.⁸

The mass of this prototype apparatus was 95kg dry, and used a total of 246kg of water.Closed-loop steady state power consumption was 0.98kW.Now-outdated lunar landers contemplated by NASA envisioned soft-landing payloads of 6 MT, compared to which the 0.34 MT of this apparatus leaves plenty of room for more.The power can be provided by two solar panels.Neither the mass nor the power were optimized for lunar operations, and can likely be made appreciably smaller.

While hydrocyclones can be used to separate particles by size and density, the size effects are generally dominant. Changes highlighted below are needed to enhance density separation.

• Smaller hydrocyclone diameter is thought to reduce the centripetal acceleration allowing for a higher quantity of lighter particles to be drawn away for the batch being separated.⁴
• Testing with a range of cone angles, starting at the extremes then moving toward central values. In tests with varying cone angles, it was shown that the highest separation efficiencies occurred between 45 and 90 degrees.⁴
• Testing with smaller underflow diameters is highly recommended as it leads to more water and light particles reporting to the overflow and heavy particles to the underflow, thus increasing separation efficiency.¹
• Multi-stage density separations would present more opportunities for lighter particles to be pulled from the mixed batch. With a single hydrocyclone and the best test (5.4% increase in concentration), it would take just 52 cycles to get adequate purity. With several cascading cyclones, the return of materials is eliminated, so it could take just a few days reach the same purity. It was shown that multi-stage cyclones recirculating underflow/underflow dramatically improve the efficiency.⁴
• A non-volatile, low-density working fluid is needed for lunar operations in a vacuum environment experiencing extremes of hot and cold.Hydrocarbons such as propylene glycol or hydraulic fluid could be evaluated.

Using a non-optimized home-built hydrocyclone density separator, technical feasibility has been proven for density-based beneficiation of actinide-bearing minerals on the lunar surface.The following conclusions have been determined:

1. Density concentration of 2.5% per pass can be achieved witha liquid-based hydrocyclone suitable for operation in lunar gravity and vacuum.
2. Concentration/separation apparatus has a mass less than 0.34 MT, with a minimum dimension under 2.0 meters, suitable for soft-landing on the Moon within an Earth-launched rocket fairing.
3. Operation is insensitive to gravity and to the orientation of the cyclone rotational axis with respect to gravity.May also be suitable for asteroid mining.
4. Separation is insensitive to the starting concentration of more-dense particles, and also to the starting mass of mixed material.These factors suggest a universal optimized design is possible.
5. Capable of concentrating a critical mass of fertile thorium within 100 days at any location on the Moon, operating with 1kW of solar panels.^9-13

This study focused on concentrating the sparse ore, and implicitly assumes excavation and materials handling pre-processing steps.Using the fuel preparation methods published elsewhere, this work demonstrates a practical approach to plentiful baseload power on the Moon.

This project is sponsored by the Richard G. Lugar Center for Renewable Energy (www.lugarenergycenter.org). The authors would like to thank the Department of Mechanical and Energy Engineering and the Department of Electrical and Computer Engineering at IUPUI for their logistical support.The guidance of Prof. J. Stang is especially appreciated.

Authors declare that there is no conflict of interest.

Design equations

$\frac{\Delta p_{CH}/\rho }{V_i^2/2g_c}=\frac{{\alpha }^2}{n}\left[{\left(\frac{D_c}{D_0}\right)}^{2n}-1\right]$

Loss Coefficient as a function of cyclone geometry

$H_{sc}=\frac{H_{\upsilon c}}{n}\left[{\left(\frac{Rc}{0.65R_0}\right)}^{2n}-1\right]$

Static head as a function of velocity head at periphery

$V{r}^n=Constant$

Velocity increases as radius approaches vortex, established empirically

$Re=\frac{V_t\cdot D_c\cdot \rho }{\eta }$

Most common approach to estimating reynolds: function of inlet velocity and cyclone diameter

$U\cdot \frac{\delta V}{\delta r}+W\cdot \frac{\delta V}{\delta r}+\frac{U\cdot V}{r}=\left(\upsilon +\epsilon \right)\left\{\frac{1}{r}\cdot \frac{\delta }{\delta r}\left(r\cdot \frac{\delta V}{\delta r}\right)+\frac{{\delta }^{2}V}{\delta z^2}-\frac{V}{r^2}\right\}$

Navier-Stokes approach to motion inside cyclone

Detailed testing procedure

1. Before starting the experiment, determine a ratio of steel and glass to test with. In practice, volume ratios were used to maintain consistency with early tests done when ranging the system’s performance: mass ratios are of more direct use, however, and were monitored during tests. The early tests were done mainly with 30% steel and 70% glass by volume, with roughly 155g steel and 115g glass, for a total mass of 270g.
2. With a ratio selected, weigh out the appropriate masses of steel and glass into a dry particle container. Volume measurements could also be used, but direct mass measurements were more accurate with the equipment available.
3. Label the container with the steel mass and the volume ratio, such as 30% to 70%. Prepare several containers at a time, either with the same or varied ratios, depending on test plans.
4. With particles ready, set up the cyclone
5. Ensure that the main water tank is full and that all power cables for the pumps are near the outlets. Also, check that the particle insertion hose is fully clamped shut and that the underflow collection bucket is secured.
6. Set the cyclone running, with the autotransformer at 90 V. Monitor the resulting operation, ensuring that the body of the cyclone fills with water and that the levels in the buckets and holding tanks are managed.
7. Once the system is stable, add water to the particle container, so that there is a thin layer above the level of the solids. Attach the particle container to the particle insertion hose, without removing the clamps. Ensure that the neck of the container is fully inside the hose.
8. Next, lift the container and hose upright, so that the particles begin to fall into the restricted part of the tube. Ensure that they can flow easily and are ready to enter the mainstream. Then, turn the autotransformer to provide 110 V, allow a few seconds for the flow to stabilize, then release the clamps simultaneously. Push the hose open, as it may remain partially constricted, and apply gentle pressure to the particle container along with a slight circular motion. Try to minimize clumping of particles if possible: the ideal is for them to flow out uniformly.
9. Observe the interior of the cyclone, watching for particles still circulating inside. Once the last particles seem to have left - typically glass - turn off the main pump. Remove the overflow and underflow buckets, and dump off the excess water, taking care to retain the particles in the bottoms. Once most of the water has been removed, scoop out the particles onto towels, spread them out thinly, and allow them to dry.
10. Once the particles are dry, set aside two open-top containers. Cover a magnet in a disposable sheet and run it over the underflow particles. Once the magnet has picked up as much steel as possible, move it over one of the containers and pull the magnet away from the covering, allowing the steel to drop into the container. Repeat this process until there is no steel that the magnet can pick up left in the underflow. Then, repeat the process twice more with the steel in the container: often there is a small amount of glass picked up during the separation process, which is best to sort out. In the end, put the remaining glass from the underflow into the same container as the remaining glass sorted from the steel. You should have one container of steel and one of glass. This process can also be done on the overflow, if that information is desired.
11. The final particles can then be weighed and compared with the original amounts put into the cyclone to determine the effectiveness of the separation.

1. Sovechles J. Exploring particle flow in a hydrocyclone classifier through positron emission particle tracking (PEPT). Ph.D. Thesis: McGill University; 2018.
2. Wills BA, Finch JA. Wills' Mineral Processing Technology. 8th Ed. Butterworth-Heinemann: Boston; 2016. 199–221 p.
3. Bradley D. The Hydrocyclone. Pergamon Press; 1965.
4. Kim BH, Klima MS. Density separation of fine, high-density particles in a water-only hydrocyclone. Mining, Metallurgy & Exploration. 1998;15:26–31.  
5. Ghadirian M, Afacan A, Hayes RE, et al. A Study of the Hydrocyclone for the Separation of Light and Heavy Particles in Aqueous Slurry. Can J Chem Eng. 2015;93(9):1667–1677.
6. Tang Z, Yu L, Wang F, et al. Effect of Particle Size and Shape on Separation in a Hydrocyclone. Water. 2018;11(1):16.
7. Neesse T, Schneider M, Dueck J, et al. Hydrocyclone operation at the transition point rope/spray discharge. Minerals Engineering. 2004;17(5):733–737.
8. Schubert PJ, Doshi J, Kindomba EM, et al. Baseload Fission Reactor for Lunar Operations. IAC CyberSpace Edition; 2020.
9. Arterburn RA. The sizing and selection of hydrocyclones; 2001.
10. Dynalene MV.
11. Schubert P. Nuclear Power from Lunar ISRU. Insights Min Sci Technol. 2019;1(1):555555.
12. Schubert P, Beatty M. Harvesting of Lunar Iron: Competitive Hands-on Learning. Annual Conference & Exposition: Pittsburgh, Pennsylvania; 2008.
13. Schubert PJ, Doshi J, Kindomba EM, et al. Baseload Fission Reactor for Lunar Operations. IAC CyberSpace Edition; 2020.