With no criticism to special relativity theory it is demonstrated with the help of a lattice with certain features, that it is feasible to reintroduce the ‘aether’ as a Lorentz invariant media. Such features lie on strings made of fibers at rest in a preferred reference system and analyzes its role as a transmission medium for the propagation both a fermion and a boson. For the approach it is used a sub algebra of Poincare that recovers the Lorentz transformation. Such sub algebra leads to a special type of graphs in which we place at ultra microscopic scale a fermion over one Euclidian space-speed graph coordinates instead of the Minkowski space-time. Finally we locate macroscopic objects and light rays in this graph and show that everything is always in a particular place at a corresponding time and discuss the anisotropy of space and the reversion of the time arrow.

We notice that serious contradictions inherent to the properties assigned to the ether provoked its demise, when it was attempted to accommodate new features imposed by observations.¹ This situation is triggered in the dawn of the laws of relativity among inertial coordinate systems,² see e.g. Einstein, Zeitschrift fur Physik, required to understand the Conrad Lorentz’s identification of those space-time conditions consistent with the electromagnetic force invariance between inertial systems, an electromagnetic theory which proved valid empirically. At the same time it is important to consider the simultaneous irruption of a quantum mechanics description valid for the recently discovered elemental particles, see e.g. Niels Bohr, Schroedinger and Louis de Broglie³

Relativity actually says nothing about the existence of something pervading the universe. It turns out that such property is found attractive, e.g. in studies of radioactivity which suggest that the empty vacuum of space would have spectroscopic structure similar to that of ordinary quantum solids and fluids.⁴ Subsequent studies with particle accelerators have now led to the view that space is more like a non-continuous, possibly like a crystal structure not detectable because of the very high energy needed to observe signatures of its breaking.⁴

This relativistic ether as a medium, space-filling substance introduced here in the interpretation of everyday phenomena is here proposed with the purpose of replacing with this Ether the more common view of a vacuum-space. We point out here that a non-empty space is the basic assumption by PMA Dirac of the home of the antiparticles like the positron, the commonly denominated ‘vacuum sea’. (See also Einstein view, e.g. Ref 2). There it is said that “a more careful reflection teaches us, however, that the special theory of relativity does not force us to deny the ether. We can suppose the existence of the ether, but we must give up attributing to it a definite state of motion”.

In the same sense Isaac Newton pronounced with respect to gravity,⁵ “It is inconceivable that inanimate brute matter should, without the mediation of something else which is not material, operate upon and affect other matter without mutual contact, as it must be, if gravitation in the sense of Epicurus be essential and inherent in it. And this is one reason why I desired you would not ascribe innate gravity to me. That gravity should be innate, inherent, and essential to matter, so that one body may act upon another at a distance through a vacuum, without the mediation of anything else, by and through which their action and force may be conveyed from one to another, is to me so great an absurdity that I believe no man who has in philosophical matters a competent faculty of thinking can ever fall into it. Gravity must be caused by an agent acting constantly according to certain laws; but whether this agent be material or immaterial, I have left open to the consideration of my readers.”

And the existence of a privilege system is a old philosophical debate relive in the Albert Einstein‘s lectures in the Olimpia academia⁶ about the definition of rotation in a totally empty universe. It was initially proposed by Newton in a thought experiment that speaks of a cube with water in rotation with respect to an observer, and questions the different reality depending on which of the two is who rotates.

In this article we develop a model were we suppose the space filled with chains of oscillators at rest in one preferred reference system that plays an active role as a transmission medium for the propagation of electromagnetic, inertial or gravitational forces?⁷ This oscillators perform spin pulses running at speed c in a linear chain.⁷ This model is isomorphic of a string theory and particles are made of a loop from fibers inside the strings.⁸ Starting from this assumptions we show that everything is always in a particular place at a particular time and it should be able to locate a photon and/or a particle in a unambiguous position of one exited “n” oscillator that must be the same for all inertial systems at every “m” cycles of this network oscillation in every coordinate system. It follows that at Planck scale nothing happen at speed other than c.

In this model we replace the point particle by a rod of length λ and ends A, B that move at speed +v over the X axe respect to this preferred reference system were strings are at rest;

$\lambda =AB=BA=\mathrm{½}\left(AB+BA\right)$

And we will demonstrate in subsection 2.2 that when measured its Compton wave length over both directions we get sub algebra to Poincare´s algebra that recover the classic Lorentz metric as the average of this 2 measures. Measuring times and distances in the 2 directions come to solve the problem of the inertial time arrow as Albert Einstein states.^9–11 We will see that the representation of objects of length λ in a Minkowski diagram (X,T) fails at ultramicroscopic scale, but when measuring the Compton wave length over this 2 directions we can plot segments A¯B and B¯A in a special type of graph (X,V) were every segment X(v) keep the Lorentz scale. The graph, although it replaces time with velocity, helps to emphasize obvious features of space time often missed in Minkowski representation.

2.1 The postulates

We will develop a model of space-time starting from a few postulates based on a lattice whose characteristics can be summarized as a network with a high rigidity, crystal structure.⁷

First postulate: This network holds elements we assume as oscillators joined by springs aligned in a way that send out spin pulses ½ up or down at regular intervals in the scale of Planck time in a linear direction. If these oscillators attached springs couple in a linear chain, this is a fiber crossed by spins.

Second postulate: Fibers group in wide strings. Every string contain the same number of fibers sending out spin pulses +½ at +c and −½ at −c and strings made of fibers that send out pulses +½ at −c and −½ at +c.

Note that from these postulates we force the construction of 2 types of strings and 4 types of fibers.

—  s strings made of s_U fibers, which send out spin pulses Up travelling at +c speed and s_D fibers, which send out spin pulses Down travelling at −c speed.

—  $\overline{s}$ strings made of ${\overline{s}}_U$ fibers, which send out spin pulses Up travelling at −c speed and ${\overline{s}}_D$  fibers, which send out spin pulses Down travelling at +c speed.

We call $S_0$ the network made of s and strings.

We add two more hypotheses;

Third: Every fermion consists of a loop from fibers inside the string. The way it moves at speed +v through the lattice is in zig-zag; over s_U fiber when going on at speed +c and over s_D fibers while coming back at speed-c.¹² The same can be said for the loop of strands ${\overline{s}}_U$ and ${\overline{s}}_D$ inside $\overline{s}$ strings.

Forth: A boson is a coupling of fibers from s and string. A photon traveling to +c is a perturb from ${\overline{s}}_U+{\overline{s}}_D$ fibers, while one traveling to −c is a perturbation from ${\overline{s}}_D+{\overline{s}}_U$ fibers.

We will illustrate the way one fermion move at speed +v respect to this lattice. We will work in 2 dimensions and in 2 coordinate systems:

—  $S_0$ of the lattice with coordinates $X´,T´$

— S of a comoving observer to the particle that moves with velocity respect to S₀ with coordinates $X,T$ .

We imagine a ruler over one s string of the S₀ system. Fibers $s_U,s_D$ are made of oscillators at a gap $l_0$ to the order of Planck length and a clock running at frequency.

${\omega }_0=\frac{\left(2.\pi \right)}{t_0}$

Taking a unit of time $t_0=l_0/c=1,{\omega }_0=2\pi$ .

From the first postulate, the most exact description of one event must be written in terms of integers unit of oscillations and position of these oscillators. Length and times in the S₀ system with coordinates X´, T´ must be written as;

$\begin{array}{l}X´=n.l_0\\ T´=m.t_0\end{array}$   (1)

where m, n ∈ N

In the comoving system S with coordinates $X,T$ the ruler of unit’s $l_0$ contract to $l_v$ units and time stretch to $t_v$ ;

$\begin{array}{l}X=n.l_v\\ T=m.t_v \end{array}$   (2)

where $l_v=l_0.{\gamma }^{-}{}^1;t_v=t_0.{\gamma }^{-}{}^1,{\omega }_v=2\pi .\gamma$ and γ the Lorentz transformation metric.

2.2 The algebra of double measurement

The simplest representation we can build for one fermion is a loop inside s string made of two strands of fibers s_U, s_D through which the spin pulses run. Let our particle be a fermion of mass $\mu =\frac{\hslash }{\lambda .c}$ made of a chain of oscillations as a small perturb over this s_U, s_D fibers as a wave of length λ and ends A, B that move at speed +v respect to S₀ over the X axe of the inertial system S (Figure 2).^3,14,15

The proper wave length in S is $\lambda =AB=BA=\mathrm{½}\left(AB+BA\right)$

The proper time in S is defined taking this particle length a unit measuring rod as a geodesic clock or Einstein clock. It may be said “toc” at each ride. Since the distance traveled by a spin pulse is the same distance traveling by a photon, we can replace pulses Up and Down by two photons; one travel back and one travel forth while actually we are talking about spin pulses.¹

To measure time and distances we will use two photons. One to travel from A´to B´ over the s_U fiber and other from B´ to A´ over s_D fiber. We define the time interval $\Delta T=\lambda /c=1$  and two Einstein clocks at fixed oscillators of the X^´ axe of S₀ preferred system were oscillators are at rest. Time is defined as the numbers of oscillations.

One clock is a two synchronized oscillators $L{´}_{+},R{´}_{+}$ over s_U fiber:

— Oscillator L^´₊record when the photon going to the right cross $A´$ ,

— Oscillator R+´  record when the photon going to the right arrive $B´$ .

And another clock over the s_D fiber:

— Oscillator R_-´ record when the photon going to the left cross $B´$ ,

— Oscillator L_-´ record when the photon going to the left arrive $A´$ .

To consider how the particle length varies when it moves respect to the system S₀ we take both distances;$A´B´\equiv X{´}_{adv}$ from s_U fiber and $B´A´\equiv X{´}_{ret}$ from s_D fiber.²

The distance $X{´}_{adv}=c.\Delta T{´}_{adv}$  traveled by a photon from the source L^´₊ to reach the end B^´ at R´+_´   is given by

$X{´}_{adv}=\left(\lambda ´.c\right)/\left(c-v\right)$   (3)

While the distance $X{´}_{ret}=c.\Delta T{´}_{ret}$ traveled by a photon from the source L´₊ to reach the end B´ at R´₊ is given by

$X{´}_{ret}=\left(\lambda ´.c\right)/\left(c+v\right)$   (4)

The Galilean sum of velocities in the measurement of λ in S does not represent a violation of the laws of Special Relativity but a consequence of the asymmetry of the arrow of time, which is the usual way in which the time asymmetry experienced in physical phenomena is called (Figure 2).¹⁶

Clearly, this asymmetry cannot be based on the fundamental laws of physics, since they are all invariant by time transformations, which is why the measurement of λ in S must be taken as the result of performing both measurements X_adv, X_ret, simultaneously and taking the arithmetic average;

$\lambda =\mathrm{½}\left(AB+BA\right)=\mathrm{½}\left(X_{adv}+X_{ret}\right).$

Then, there must be a factor that relate the length λ in S and the distances X´_adv, X´_ret in S₀ for both events of emission and absorption of the photon.

It is easy to verify that this factor is

$\chi =\sqrt{\frac{c+\nu }{c-\nu }}$   (5)

And this fundamental relation was created by Bondi with the name of k constant.¹⁷

The relationship sought results:

$\begin{array}{l}X{´}_{adv}=\lambda .\chi \\ X{´}_{ret}=\lambda /\chi \end{array}$   (6)

And also the inverse;

$\begin{array}{l}{X}_{adv}=\lambda ´.\chi \\ X_{ret}=\lambda ´/\chi \end{array}$

The rod length in S´ is

$\lambda ´= \sqrt{X_{adv}+X_{ret}}$   (7)

And also the inverse $\lambda = \sqrt{X{´}_{adv}+X{´}_{ret}}$

From (3) and (4) we recover the Lorentz metric: 

$\lambda ={\lambda }^{\prime }\sqrt{\frac{c}{c+\nu }.}\frac{c}{c-\nu }=\gamma .{\lambda }^{\prime }$

2.3 Proper units

From eq.(2) distances in S must be express in integer units of oscillators at a gap l_v at rest in S₀

$\begin{array}{l}{X}_{adv}=n.l_v.\chi \\ X_{ret}=n.l_v/\chi \end{array}$   (8)

If these lengths are the internal movement of a fermion of mass $\mu =\frac{\hslash }{\lambda .c}$ running at speed v over 2 fibers inside the string we can express its Comptom wave length as the real distances traveled by the spin pulses as the arithmetic average of $X_{adv},X_{ret}$

$\lambda =\mathrm{½}.(X_{adv}+X_{ret})=n.\mathrm{½}(\chi +{\chi }^{-1}).l_v=n.\gamma .l_v=n.l_0$

It´s clear that despite the proper units in S system are in l_v units of oscillators of eq. (2), this 2 measures require the proper wave length λ must be written as the average of both ultramicroscopic measures and the wave length of a fermion in S must be written as³ $\mu =\frac{2.\hslash }{c.(X_{adv}+X_{ret})}=\frac{\hslash }{\lambda .c}$

We conclude that the particle´s lengths in S and S₀ will be expressed by a unique “n” amount of units.

$\begin{array}{l}\lambda =n.l_0\\ \lambda ´=n.lv\end{array}$

It follows from (1) and (6) that in S₀ units the distances travelled by this photons can be expressed by natural numbers:⁴

$\begin{array}{l}X{´}_{adv}=\left(n.\chi \right).l_0\\ X{´}_{ret}=\left(n/\chi \right).l_0\end{array}$   (9)

And in l₀ units of eq. (1) this distances can be expressed in S₀ system by the same set of natural numbers than eq. (8) were X´_adv, X´_ret refer measures taken in the S₀ system were the zig-zag movement take place:

What we state is that everything is always in a particular place at a particular time.

In relation to the time events were characterized for a unique integer “m” number. But taking the 2 measures over S system our Einstein clock sound like a short ”tic” follow a long ”tac”, and proper time is also t₀.

Clock frequency transform as ω_v = ω₀.γ while the wave associated with the particle transform as ${\nu }_v={\nu }_0.{\gamma }^{-}{}^1$ .

We conclude that even the proper units in every system are l_v, t_v, for particles defined as the third postulate it must be express with invariant m, n numbers and well defined l₀, t₀ units of the S₀ system.

This feature cannot be seen in Minkowski´s diagram where a point particle neglect the internal zig-zag movement of elementary particle topology mixing s_U, s_D fibers as the average in a single X axe of l_v units of eq. (2) and in a not Euclidean plane.

¹We emphasize that from the iv postulate this is not a real photon but a half part of it because actually a real photon is a wave traveling over s_U and s¯_D fibers at speed +c or from s¯_U and s_D fibers at speed −c from s + s¯ strings.

²adv= advance, while ret=return

³But λ^′ is not a length made of X_adv, X_ret chain of oscillators over S. The opposite relation:

λ^′ = ½ (A^′B^′ + B^′A^′) = ½ (Xa′ dv + Xr′ et) will implies oscillators over S system and is not valid.

⁴The high value of n grant that n/χ, n.χ also N.

To show that everything is always in a particular place at a particular time we will represent geometrically the position of one fermion in both a Minkowski and a special type of graph were we split the X axe in the s_U and s_D fibers.

3.1 Simultaneity and locality

We will mark the four events defined in 2.2 labeling the oscillator L^´₊ as (1) and as (4) over s_U fiber and R´ and L´ as (3) over s_D fiber.

We trace in Figure 1 the world sheet of this particle with ends A, B in Minkowski diagram over the X^´, T ^´ axes as if it were the S₀ system of oscillators showing the zig-zag as $\mathrm{½}{X}_{adv}+\mathrm{½}{X}_{ret}$ . In Figure 2 we represent the static position of a small perturb over a arbitrary small length D in this special kind of graph splitting the cycle of moving back and forth in two traces; the zig X_adv = AB (Figure 2a) over s_U fiber and the zag X_ret = BA (Figure 2b) over s_D. The X(V) axes are at Lorentz scale and objects remain inside triangles limited by the interval ∆T = D/c =1.

Figure 1 Time line of a point particle T in a zig zag from A to B and from B to A.

Replacing the time coordinate of the Minkowski diagram by V, the (V,X) plane is Euclidean, and let us plot the location of the ends A, B over the X(v) axe and over the X(0) axe at Lorentz scale marking in the ordinate the oscillators were event take place at an angle ∆T = 0 and in the hypotenuse events will take place in the future at angle ∆T = 1 at the same natural number of oscillation t₀, t_v. In Figure 2a the event (4) will take place at a fixed oscillator labeled with the same integer n.χ units of l₀, l_v showing X_adv, X´_adv at Lorentz scale as well as time as the angles ∆T, ∆T´_adv.

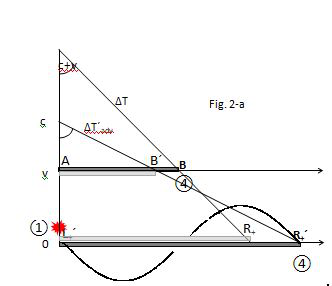
Figure 2a A photon in A ≡ L^´₊ and in B ≡ R´₊ at an angle ∆T´_adv > ∆T = 1 and sinus elongates.

The same can be said in Figures 2b for the event (3) over the s_D fiber labeled with integer units of l₀, l_v at Lorentz scale as the times as angles ∆T, ∆T´_ret. Taking arbitrary angles ∆T, locality in frames is clear everywhere (Figure 3). In Figures 2a&2b events (1) and (2) take place at ∆T = ∆T ^´ = tg(0) while events and (4) take place at ∆T and ∆T ^´ intervals at Lorentz scale. Events take place always at a well define “n” cell at a particular “m” number of oscillations. But in Figures 2a&2b the interval ∆T´ has a flagrant asymmetry and it must be defined taking into account the direction of the arrow, which turns out to depend not only on the speed but also its sign.

In Minkowski representation simultaneity fails at both ends of the world line. Clearly every non local event must be defined adding or subtracting the term $X=c.T$ , and the only valid coordinate transformation is the null coordinate.

In Figures 2a we graph the particle in the comoving system S setting the interval as the time to take the photon to cover a regular segment of length D = c.∆T with ∆T = tg(π / 4) = 1 from A to B and show the X´_adv strand on the X´ axis of S₀ system were the event take place over oscillators labeled R+;$R´+$ at Lorentz scale in such a way that a perturb over the L´₊ oscillator start recording spin pulses over s_U fiber. The distance $X{´}_{adv} =c.\Lambda T{´}_{adv}$ spread out an angle greater than π/4.

In Figures 2-b we locate in the same frame the X´_ret strand on the X´ axis and show the interval ∆T = 1 to take the photon to go from B at $L´$ oscillator to A at $R´$ oscillator such that a spin pulse in $R´$ start recording over s_D  fiber.

The distance $X{´}_{ret} =c.\Delta T{´}_{ret}$ sweep out an angle lower than π/4.

In this graph we can see clear that achieving the postulates I) to IV) causality and simultaneity preserve and also be possible to describe the dynamic over both a comoving system and a lattice who plays an active role for both electromagnetic and matter waves in a Lorentz invariant media.^14,15

But on such a lattice nothing happens at speeds other than c, and at ultra microscopic scale we must take both directions of the arrow of time to obtain the Lorentz metric.

3.2 Lorentz ratio in Euclidean geometry

It is easy to verify in these diagrams that the axes preserve the Lorentz ratio of the length X(v) with the length X(0).

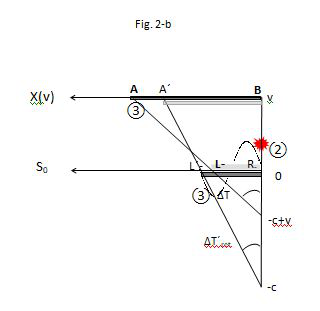
Figure 2b A photon in B ≡ R´₋ and in A ≡ L^´₋ at an angle ∆T´_ret < ∆T = 1 and sinus shorted.
Figure 2 The particle of length D = ¹ (AB + BA) as a thread of fibers s_U , s_D seen from both systems S₀ and S system showing the trace of spin pulses from A to B (left) and from B to A (right).

Comparing segments, it is verified in Figures 2a that the triangles

$(L´+)(c)(R+´);(L+)(c+v)(R+)$ , achieve

D/c = X_adv/(c+v)

 X´_adv/c = D´/(c-v)

From this we obtain $D/D´=\left(X_{adv}/X{´}_{adv}\right).{\gamma }^2$

Similar relation is verified in Figure 2-b between D, D´, X_ret,, X´_r et.

Because the linear relation between length at rest and length in movement we obtain:$D/D´=X{´}_{adv}/X_{adv}=X{´}_{ret}/X_{ret}=\gamma$

Despite the internal oscillation inside the string that every elementary particle are made of, movement of larger objects can also be described in terms of invariant natural numbers n, m were the Lorentz contraction is assumed not only for fermionic matter but also the units of vacuum and also for the Planck length.

3.3 Application to larger objects

We can extend this result to larger objects like a real clock over the parallel arm of one interferometer of arbitrary length D. We will use now a real photon merging and mixing both s, s¯ strings such that X, X^j will not be the coordinate inside fiber but S, S₀ inertial systems coordinate (Figure 3). The word “frame” now apply to this new type of graphics in which we remove the time coordinate and plot a clock measuring-rod ∆T = 1 of one arbitrary length D in both Minkowski and frames schemes. Choosing one direction +c or c, frames 2-a or 2-b allows us to visualize the real location of one-way photon over the arm in terms of oscillators labeled with invariant n, m numbers in a closed interval ∆T = 1. We´ll label L´, R´ in the X´ axe the oscillators that match with the semi platted and plated mirrors A and B. Choosing the +c photon, we must chose the triangle of Fig. 2-a. In Fig. 3 we chose the middle of the interval were the photon travel from A to B in S but from L´ to R´ in S₀ over a group of strings for the event of emission a photon synchronized in A with a source in L´ represented by the angle ∆T₁ at the past. If we plot the frame of the half time of this semi interval ∆T = 1 we get 2 identical triangles; one from the past in L to present in T and another from the present in T to the future in R. As a requisite for a good background-free theory, the spatially separated events lie outside the triangles and have no representation. Despite Figure 3 exhibit the same event than Figure 1, an advantage of frames vs. Minkowski diagrams is that it allows us to visualize the exact location of the photon over the parallel arm of the interferometer at any particular time and plot the ends A and B over a set of Cartesian axes X(v) ordered according to velocity v of the rod in a Galilean sum 0, v, c, (c + v) or −v, 0, (c − v), c.

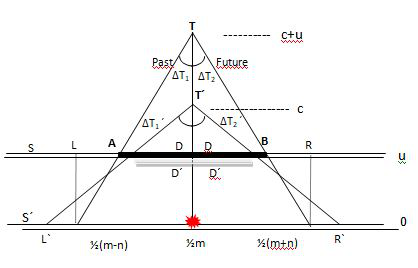
Figure 3 The parallel arm of a large interferometer with a single photon in the middle seen from 2 systems: S with inherited unit tv, lv and S´ with proper units l0, t0, but involved the same number of oscillators of the ether. (Double trace indicates s, s¯ strings).

In Minkowski representation, the angle between the ordinate T´ and the world line T is the speed of an object; angle α = 0 is an object at rest while the angle α = π/4, -the world line of a photon- a speed c. In this diagram, the angle α is not the speed but the interval ∆T = tg(α), and T = tg(0), the present. The interval α = π/4 is the time ∆T = 1 to take a boson to travel one arbitrary rod of length D and ends AB over s_D and s¯_U fibers.

We had plot over a arbitrary clock measuring rod the one way photon traveling over this ether. But these rods are made of fermions. A single fermion inside s or s¯ string move in zig-zag with velocity v respect to the lattice.

In fact $\left(X{´}_{adv}-X{´}_{ret}\right)/\left(T{´}_{adv}+T{´}_{ret}\right)=v$   (10)

What we state is that if this ether exists, space is not isotropic, and there is a big difference between the times in the two ways of the light signal transit.

Removing time we can see clear the real distance a photon travels in the arbitrary interval ∆T = 1 over this two directions.

3.4 Example; the train and the embankment

Let us show that all events occur at a particular time and place characterized by a set of integers units of space-time of vacuum in the classical Einstein example of the train and embankment.¹³ To avoid fixing the two flashes in the embankment system we propose to replace it by four electrodes, two with negative charge located on the embankment indicated with the letters L and R, and two with positive charge located on the train indicated with the letters A and B , so that when B meets R there is a spark, and another when A meets L (Figure 4).

Choosing the time at which the arrival of the photons is simultaneous in both systems, the observer O^´ would not be in the center of the train but at a distance l₂ from A^´ and r₂ from B^´ given by equations (6).

Calling D = LR/2

l₂´= D/χ                   r₂´= D.χ

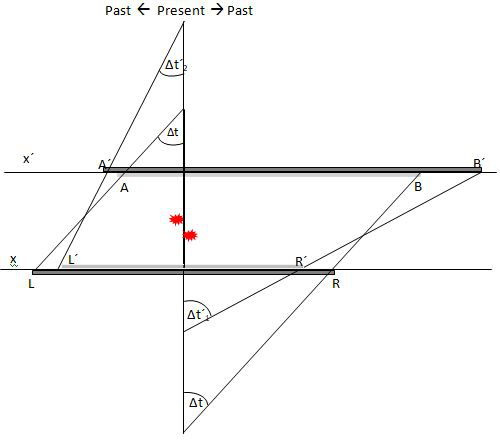
Figure 4 In dark trace both embankment and train at rest in S and S^´ system in l₀ units at a gap of speed v. In gray trace the image of the moving object in l_v units.

Because the different speed of clocks we clearly see that events that were simultaneous in the past were not simultaneous by now, and also the time asymmetry. But when the present line move closer this difference decrease to void at a gap 0 while increase at the opposite direction. Again, this frame comply the linear relation between the lengths in S and S^´ of the form $l_2´=\gamma .l_2.$

$\begin{array}{l}D´/\left(c+v\right)=l_2´/c\\ D´/\left(c-v\right)=r_2´/c\\ D/c=l_2/\left(c-v\right)=r_2/\left(c+v\right)\end{array}$

From this we get

$D/D´=(l_2/l_2´).{\gamma }^2$

If AB = n.l₀ and LR = m.l₀ the one and only system in which events look simultaneous is the system S that have a speed v that makes n.l₀ = m.l_v; here the parallelogram LABR. And also ∆T is symmetric as everyday experiences with light rays exhibits.

The strong evidences about the existence of a preferred aether frame¹⁸ and the anisotropy of the one way speed of light will be complemented with some discussion about the aftermath of this theory.

4.1 The non observance of S₀

We had seen that this loop model for fermions can be extended from ultramicroscopic scale to larger objects like an interferometer or the embanking taking all the four kind of fibers grouped in two strings s, s¯ that conform the S₀ system. Taking the both directions of the arrow, our Einstein clock over the Planck time sounds like a short “tic” follow a long “tac”, and proper time is t₀ relativistic inertial system. Since we lack a method to identify such S₀ system, we cannot find the χ constant who relate X´_adv, X´_ret to λ and distinguish l_v from l₀. Then χ turn out indeterminate and we can consider any two systems S and S^´ without the need for one of them to be the S₀ system of the lattice.

We can also save the disagreement between frames and Minkowski adding the latter thin light cones over the world sheet of every fermion to show the inertial time arrow asymmetry, and the trajectory of one fermion like a electron¹² must be described by means of a asymmetric zig-zag path over light cones in a Minkowski’s graticule.¹⁷ But the light cone background does not necessarily be the substrate, as Bondi clearly demonstrates. In every comoving coordinate system every fermionic matter who moves at speed +v respect to S₀, the trace ½ X_adv from (1) to T is longer than the ½ X_ret from T to (2), but we don´t need it be the lattice. Every S^´ observer in T who takes one measure receiving a photon from both ends will get equal values for the length of D eq. (6).

The proportionality factor is:

$D=X{´}_{adv}/{\chi }_u=X{´}_{ret}.{\chi }_u$

Where χ_u is the Bondi´s k constant:¹⁷

${\chi }_u=\sqrt{\frac{c+u}{c-u}}$

But depicted D is still maximum in the system where the interferometer is at rest:

$D=\mathrm{½}\left(X_{adv}+X_{ret}\right)=D^{´}.\left({\chi }_u+{\chi }_u{}^{-1}\right)=D^{´}.{\gamma }_u,the{\chi }_u$  constant refer to a sub algebra that compels to take both directions to recover the Lorentz coordinate transformation:$l_0={\gamma }_u.l_u={\gamma }_v.l_v=\mathrm{....}$

The particle is a wave constantly in phase with oscillator´s system, and S₀ system has nothing special.

Therefore, we must base all the development on our ultramicroscopic Einstein clock measuring-rod of length D = n.l₀ taking as a unit the time to take spin pulses to travel in both directions.

But because the larger unit ∆T = 1 involved, the concept of locality broaden.

4.2 The arrow of  time

Now we will lay down that the reversion of the arrow of time is not a valid proposal. We can see with the help of frames that the arrow of time only can evolve in the arrow of spin pulses no matter how the system evolve (i.e. time events do move solely in the future). Further, we state is that the inversion of the trajectory changing speed u by u is not a valid procedure because the asymmetric transformation implies to change from large X_adv strand over the s_U fiber and short X_ret over s_D to the opposite as clearly see in Minkowski diagram Fig. 1. Also a photon traveling over s_U /s¯_D fibers cannot be move to the opposite fibers. A returning photon only can be done by a mirror. The reflection in the mirror implies a photon change from $\raisebox{1ex}{$S_U$}\!\left/ \!\raisebox{-1ex}{${\overline{S}}_D$}\right.$ to $\raisebox{1ex}{$S_D$}\!\left/ \!\raisebox{-1ex}{${\overline{S}}_U$}\right.$ fibers.

Presented are consistent arguments that starting from postulates enunciated in 2, a hypothetical type of Lorentz invariant ether must be introduced. But fermionic mater movement is only possible riding over the fibers like a surfer over a wave; a larger time going forth, and a shorter time going back as a surfer does when the wave exhaust. If the surfer is a fermion, the speed is the result of a zig-zag movement with average speed v of eq. (10) and there is only one arrow of time. We conclude that it is possible to locate in space and time both fermions and bosons as a perturb from a lattice with invariant natural numbers for all reference systems. We settled that the Lorentz transformation presents compatibility with a sub algebra which include the existence of such preferred reference system. But it does not imply a breakdown of the Lorentz invariance at larger scale. Such a model entail Minkowski diagram must be modified adding this ultramicroscopic zig zag and it’s clearer from such a lattice to split the X axe in s_U, s_D fibers like Figure 2&3 reveal that the special relativity does not deny the possibility of the existence of a privilege system that may possess structure, even though Einstein himself pointed out, the idea of motion may not apply.

We raise to the category of fundamental law the next axiom:

At the Planck scale, nothing happens at speeds other than c and the only valid coordinate transformation is the null coordinates.

What we state here is the possibility of the existence of the ether consistent with the laws of nature as we currently understand them, not as a entity that do nothing but a field capable to absorb or supply energy, and the last responsible for the inertial⁷ forces.⁵

Considering this S₀ substrate the background of all fields as something real we also conclude that at microscopic scale it is not possible to think in point particles. If we postulate this network made of fibers grouped in strings made of a large enough quantity n of oscillators, the maximum reduction that we can make for a particle lie in strands of unequal lengths X´_{adv ,} X´_ret made of integer number of oscillators from the lattice, but look of equal length λ measured in the system S where it is at rest.

We must choose in 2.1 this set of postulates in accordance with the use it in⁷ a model of spin network in which these oscillators perform spin pulses, and internal movement take place inside fermions with this spin pulses circling around at speed c. It is also suggestive that there is an unique way in which universal physical constants combine to give one universal unit of length; the Plank length l_p, that because Relativity will be only valid in a privileged metric system.

Also we show in⁷ that because the change of inertial system implies the change in the Planck scale, this is a way by which the ether store not only kinetic energy but also gravitational forces. But even if you do not subscribe the properties and postulates 2.1 and developed in about the existence of this S₀ system, the frame representation of objects in Figures 2–4 are still valid, and there are reasonable consistent arguments to reintroduce the ether.

In relation to the reversibility of time, by the impossibility of any perturbation be that a fermion or a boson to surf against the pulses, the inversion of time is not a valid proposal and there is only one arrow of time.

The trajectory of every particle must be described by the transformation (6) which is clearly asymmetric, and not by Lorentz, which is symmetric. But taking both directions for the Compton length of elementary particle we recover the classic Lorentz metric.

⁵Inertial forces = systems with l_v < l₀ imply m > m₀.

We thank the late Mario A. G. J. Castagnino, who with his brilliant ideas encouraged this work.

The authors declare that there is no conflict of interest.

1. Kracklauer AF. The Michelson-Morley experiment in ontic and epistemic space.
2. Albert Einstein, Reader in University of Leiden, May 5 1920. Translated from German by Methuen, London; 1922.
3. Louis de Broglie, Interpretation of quantum mechanics by the double solution theory. Annals de la Foundation. 1987;12(4).
4. Laughlin, Robert B. A Different Universe: Reinventing Physics from the Bottom Down. 2005.
5. Isaac Newton. Principia. London; 1687.
6. David Hume. Lectures with his friends Solovine. Habicht.
7. Daniel Levi. About Spin Network, Fibers and Strings for Quantum Gravity.
8. Gambini R. Loop Quantum Gravity.
9. Einstein. Letter to Hermann Weyl, 19 April 1918, Synge: 1960, Geroch; 1972.
10. Heinrich Zangger letter. 1915.
11. Sommerfield letter. 1915.
12. David Hestenes. The Zitterbewegung Interpretation of Quantum Mechanics. Found Physics. 1990;20(10):1213–1232.
13. Joseph Levy. Basic concepts for a fundamental aether theory.
14. Gauthier-Villars. Une interpr´etation causale et non-lin´eaire de la m´ecanique ondulatoire. La th´eorie de la double solution. Paris: 1956; English translation Amsterdam; 1960.
15. Gauthier Villars. La th´eorie de la mesure en m´ecanique ondulatoire. Paris; 1957.
16. The arrow of time: from universe time-asymmetry to local irreversible processes. Foundations of Physics. 38:257–292.
17. Bondi H. Assumption and Myth in Physical Theory. Cambridge University Press; 1967.
18. Ruggero Maria Santilli. Neutrino and/or etherino?