Using simplifying assumptions, a region or time in the universe is conceived, which allows for a state constituted solely by a gaseous plasma subject to the current laws of gravity and electromagnetism to exist. Under these conditions, it is proposed that the presence of a portion of that medium, organized in a highly symmetric magnetic field and plasma structure, possesses the symmetry of a torus. We resort to the fact that magneto hydrodynamics (MHD) is the common state of this medium and that it has the property of attaching to it the mass. (I.e. in the language of MHD the mass of the torus is assumed to be magnetized.) The solution to this MHD equilibrium of the matter of the torus, which prevents it from coalescing through the gravitational pool, is presented. Further, analysis shows that a gravitational field generated by the torus may be capable of attracting the other, non-magnetized matter, under the influence of the torus’ gravitational pool. In this way it is shown that the torus shaped MHD structure, under the discussed conditions, satisfies essential properties, like having large regions where the Keplerian mass motion cannot be present. A scenario consistent with a few key properties of proto-nebulae in equilibrium is presented and considered.

Keywords: astrophysics, MHD, magnetic force free analytical solutions

We present a simple stage in the evolution of nebulae, at some point in time, before its either gentle or dramatic metamorphosis into becoming an ordinary galaxy. We may locate this scenario at some remote time and its location at some remote place, depending on our favorite big-bang model of the universe,¹ or other possibilities including ‘a static,’ time independent solution, and or Kaluza – Klein models.^2–4 If we assume a time epoch in the universe’s existence, a few hundred thousand years from its beginning in an expansion-inflationary process,⁵ following the re-ignition period. In this scenario we consider a possible quasi-equilibrium stage where the presence of currents, i.e. electromagnetic fields, would be enough to allow a state of plasma neutrality and dominance of the magnetic force in an ionized plasma, and constituting a hydromagnetic state, with which we are well acquainted theoretically,^6,7 and which was later detected with the automat observations first near the Earth and later everywhere in the heliosphere, and more recently beyond into the local interstellar medium.⁸

Considering that the Maxwell and gravitational laws applied then, like they do today, we propose that self-organization of matter, plasma, and magnetic fields may have been produced in a variety of regions of the early time’s structures. After the introduction, there is a presentation of the model in Section 2. Conclusions are drawn in Section 3.

A simple proto-nebulae

We consider that self-organization was generated in magnetized plasma and we assume it to be simplest. Hence, we use the simpler mathematical expression of a self-organized structure of the kind discussed earlier,⁸ Figure 1 shows a representation of the structure, a torus in which the extension of the torus boundaries corresponds to the limit where the axial field reverses its direction.

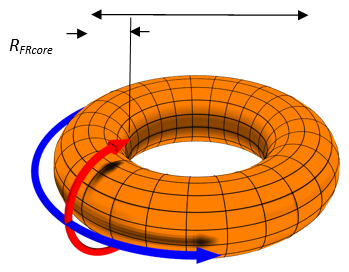
Figure 1 Approximately cylindrical with minor radius R_FRcore, and major radius R_cFR.

When assuming ideal MHD conditions, i.e. a scenario in which the self-gravitational field of the structure would curve the magnetized matter, thereby providing stability and long life to the structure (ideal MHD assumes zero diffussion of the B-field)^6–8 with the following solutions in toroidal coordinates:

$B= B_0[J_0(A(\rho ,f))e_x+H{J}_1(A(\rho ,f))e_{\varphi }],$    (1)

where its solution with

$A(\rho ,f)=a\left(\rho \right)[1+\rho /R_{cFR}(cos(f)–|sin(f)|)]$   (2)

would be the time stationary limit of the solution presented earlier⁹ in a different context,

where $a(\rho )=A\rho ,andA=j_0/R_{FRcore},J_{0,1}$ are the well known orthogonal, grade 0 and 1, cylindrical Bessel functions of 1^st kind,⁹ and the value of $\rho =R_{FRcore}$  defines the radius of ‘the circular cross section’ of an approximated cylinder-section of the torus at the location where the axial magnetic field has its first node, is identically zero, i.e., $J_0\left(j_0\right)=0$ . In this case study there is no volume (Vol) change of the matter magnetized structure with time. A more general case is considered elsewhere.^10,11 As usual we evaluate the convective current $J_c$  using $(J_c=Ñ\times H)$ ,¹² up to $O{\left(R_{FRcore}/R_{cFR}\right)}^2$ , with the accuracy dependent on the ratio of the minor $\left(R_{cFRcore}\right)$ to major $\left(R_{cFR}\right)$ torus radii, and which gives next the convective current $J_c$ components

$J_{cx}\left(modified\right)=A/{\mu }_0\{H{B}_x[1–2\rho /R_{cFR}(cos(f)–|sin(f)|)]+\Delta j_{cx}\}$   (3.a)

with

$B_x=B_0{J}_0(A(\rho ,f)),and\Delta j_{cx}=\rho /R_{cFR}(cos(f)–|sin(f)|)J1(A(\rho ,f))/A(\rho ,f)$ , the other two components of J_C being:

$J_{c\rho }=–A/{\mu }_{0}H{B}_f\rho /R_{cFR}[sin(f)+{\partial }_f|sin(f)|]$   (3.b)

$J_c{}_f=A/{\mu }_{0}H{B}_f[1–2\rho /R_{cFR}(cos(f)–|sin(f)|)]$   (3.c)

where $B_f=H{B}_0{J}_1(A(\rho ,f))$ is the polar component of the magnetic field density B. and $H\left(=+1or–1\right)$ is the handedness of the FR, and Equations (3.a – 3.c) are the corrected expressions¹¹ Notice that in this case the equations simplify by neglecting time dependencies, i.e. steady state only, considered here. These three components of J_c can be visualized with the help of (Figure 1) which allow to understand the geometric shape of the circulation of the MHD convection current, with components from Equation 3.a to 3.c, respectively flowing along the main axis ‘x’ of the torus, current J_cx, the minor radius ‘ρ’ of the torus, I,e current J_cø, , and along ‘ø’ the poloidal current, J_cø , where ‘x, ρ, and ø ‘ constitute a right handed coordinate system.

Next we drop subindices for R_cFR, and instead we use R. The summatory of all ‘torus’ elements and gravitational forces acting on each infinitesimal element ‘δM_Torus‘ at the torus’ locus is oriented to the center of the torus, defined as

$F_g\left(\delta M_{Torus}\right)=–G{M}_{Torus}\delta M_{Torus}R\left(\delta M_{Torus}\right)/{\left|R\right|}^3$   (4.a)

for circular symmetry of the simple case of homogeneously distributed matter in a magnetized field (defined in Equation 1). Also, any mass particle m located at the distance from the center of the torus | r – R| is bound to feel such gravitational pull,

$F_g\left(m\left(r–R\right)\right)=–G{M}_{Torus}m\left(r–R\right)/{\left|r–R\right|}^3$   (4.b)

similar to the one shown in Equation 4.a for a coordinate system with its origin at the center of the torus.

For the expression of the vector potential A, notice that the corrected expression¹³ is easily generalizable to the case of a torus. Once with the expression for the magnetic field and the current, it is easy to find the equilibrium condition for

$\sum F=0$   (5)

where we here solely consider magnetic and gravitational forces, i.e.

${\int }_M{F}_g\left(d{M}_{Torus}\right)dM+{\int }_{J}d{J}_{C}XB=0$   (6)

and, considering the solution of Equation 6 in¹¹ for a truncated torus, we proceed to the generalization of the simpler case of a whole torus developed here, which for us corresponds to the simplified equilibrium expression

$–G{\left(M_{Torus}\right)}^2+(25{\mu }_0/4) [{\Phi }_f{}^2]=0.$   (7)

The mass of the torus (M_Torus) and the poloidal magnetic flux (Φ_ϕ) forces in equilibrium are simply related as shown in Equation (7). In this way we obtain, for a simple limit, the condition for matter to be attached to the ‘protogalaxie magnetic field’ generated by convective currents, which stabilize the matter in a cold frozen matter condition. Preliminary studies^13,14 suggest that this, “a stable structure.” will possess specific thermodynamic properties characteristic of a diamagnetic environment. This stability condition could be subject to a variety of possible disruptions and that study is beyond the scope of the present work.

Notice that the model does not consider the presence of angular momentum, even though its presence is well known in most galaxies¹⁵ (Most likely the centripetal force associated to a “low velocity” simplified here to a rigid rotation of the structure would add to its stability respect to the pull of the gravitational force.)

A possible scenario is that the curvature of the magneto matter structure could be provided by the re-ignition process after the appearance of supermassive stars of relatively short life cycles, followed by their gravitational collapse after a primordial cooling following the big-bang as presented in hypotheses elsewhere.¹⁵ Here, on simplifying grounds it is given consideration to the possibility of the evolution, under those conditions, of the highly symmetric MHD magneto-matter with a torus shape presented in Figure 1. From our analysis, a large, symmetric, magnetic-matter is connected to the generation of point-like gravitational center at the locus of the MHD torus–structure discussed. Matter in the proximity of this center –of the torus MHD structure considered– could flow to, and possibly generate after a few hundred-thousand years a denser central region in the proto-galaxy.

When thinking of the possible origin of the angular momentum generation, a succession of coherent push by the infalling matter to the center of the major radius of the torus (possibly a proto-galaxy with a denser center and an eventual subject in a line of study to be developed). This condition could introduce angular momentum into the torus magneto-matter system. The frozen nature of the structure subjected to a rotational equilibrium would naturally make the internal part of the torus (here we call it protogalaxy) rotate in a rather synchronous way, with its external region providing a feature that could resemble the rotational pattern of increasing velocity of rotation with the distance from the center of the galaxy. This rotational pattern is today well validated from many very accurate observations, beginning approximately after the mid past century,^15,16 This very intriguing rotational pattern has been the engine of a large amount of work for the last several decades due to the fact that we are now well aware that this rotational pattern of galaxies goes contrary to the well understood Keplerian motion, which inspired the theory of universal gravitation by Isaac Newton.

Further, notice that the presented scenario does not require the pre-existent presence of earlier black holes, the kind which could have occurred because of the collapse of the primordial super-massive stars,¹⁷ and which may have constituted the seed for the possible appearance later of a primogenious kind of galaxies, of current uncertain existence.

To my father for his love of a whole life, and my late wife for her patience with my love for science. To my son Santiago Berdichevsky for a careful check of the English.

Authors declare that there is no conflict of interest.

None.

1. Weinberg S. Cosmology. Oxford, UK, Oxford Univ Pr. 2008.
2. Ponce de Leon J. Equations of Motion in Kaluza-Klein Gravity Reexamined, Laboratory of Theoretical Physics, Department of Physics University. 2018
3. Kaluza Theodor. Zum Unitätsproblem in der Physik. Math Phys.1921;966–972.
4. Klein Oskar.Quantentheorie und fünfdimensionale Relativitätstheorie. Zeitschrift für Physik A. 1926;37(12):895–906.
5. Senatore L. Lectures on Inflation, Stanford Institute for Theoretical Physics Department of Physics, Stanford University, Stanford, CA 94306 Kavli Institute for Particle Astrophysics and Cosmology. 2016
6. Alfvén H. Existence of electromagnetic-hydrodynamic waves. Nature.1942;150:405–406.
7. Alfvén H. On the Theory of Magnetic Storms and Aurorae. Tellus.1958;10(1) l:104–116.
8. Berdichevsky. On the equilibrium of a extremely extended and dilute magneto-matter state subject to its weight. APS March Meeting. 2016;61(2).
9. Abramowitz, M Stegun, IA. Handbook of Mathematical Functions, 9th Ed. Dover, New York; 1972.
10. Berdichevsky DB. On Fields and Mass Constraints for the Uniform Propagation of Magnetic-Flux Ropes Undergoing Isotropic Expansion. Solar Phys. 2013;284:245–259.
11. Berdichevsky DB. Erratum. Solar Phys. 2019;294:167.
12.  Jackson D. Electrodinámica Clásica. Translation G Marsal, 2nd ed. La Alhambra, Madrid, Spain; 1963.
13. Berdichevsky D B, K Schefers. On the thermodynamics and other constitutive properties of a class of strongly magnetized matter observed in astrophysics. Astrophysical J. 2015;805:70:13.
14. Burlaga LF, JF Lemaire. Interplanetary magneti holes theory. Journal Geophys Res Atmospheres. 1978;83(A11):5157-5160
15. Rubin VC. Rotational Properties of 21-Sc Galaxies with A Large Range Of Luminosities and Radii, From Ngc 4605 (R = 4 Kpc) To Ugc 2885 (R = 122 Kpc). Astrophysical Journal.1980;238:471–487
16.  Rubin VC, WK Ford, Jr Kent. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. ApJ. 1970;159:379–403.
17. D Whalen, E Glover, Patrick, et al. On the detection of supermassive primordial stars. Astrophys J. 2021;915(110):10.