A simple model for the variation of CubeSat temperature along its orbit is presented. First, an analytic solution for the satellite temperature variation with time when subjected to a bistable heat source: two segments with piece-wise constant power, such as orbits with an eclipsed segment when the Sun is not directly visible, is considered. The model assumes that at a given time a single temperature applies to the entire satellite body. Discussion is focused on CubeSat satellites in low-Earth orbits, the uncertainties in predicted temperatures due to uncertain input parameters, and it emphasizes the importance of the satellite thermal inertia in setting the amplitude of the temperature variation along the orbit. This simplified “spherical cow" model is suitable for studying the relative effects of surfaces with different emissivities, the effects of small changes in the solar flux between June and December, the impact of thermal inertia, and as a “sanity check" for the results obtained with numerical thermal models that utilize detailed geometrical and thermal descriptions of all satellite components. It was found that the mean satellite temperature depends on the extreme values of steady-state equilibrium temperatures for eclipsed and non-eclipsed parts of the orbit, and the duration of the eclipse relative to the orbital period; in contrast, the amplitude of temperature variation around the mean temperature is by and large controlled by the satellite thermal inertia. A numerical model with arbitrary time dependence of the heating power is also developed, including its dependence on the satellite temperature, and validated it using analytic solution for a bistable heat source. Analysis of a typical 2U CubeSat shows that low temperatures are more worrisome than high temperatures, and that low temperatures can be mitigated by active temperature control such as releasing heat when the satellite is in eclipse using electrical energy stored in batteries that are charged during non-eclipsed portion of the orbit.

Keywords: satellites, cubesat, radiative transfer, analytic solution

Over the last two decades, the concept of a small modular satellite named CubeSat¹ has become extremely popular to date about two thousand satellites were launched or are in preparation stage.² CubeSat projects have both scientific and educational values, and are supported by many universities as well as space organizations such as NASA and ESO. When designing a satellite, it is crucial to establish that the temperature variation for each component will be within its operating range. In practice, professional engineering tools (such as Ansys framework) and numerical analysis are used to analyze complex systems. Nevertheless, approximately correct temperature estimates and physical insight can be derived even using simple analytic models. Such models can be used as a “sanity check" for the results obtained with complex thermal models that include numerous input parameters, and for fast input parameter exploration (e.g., runtime for a numerical transient model using the Ansys code can be several hours). Simplified models are also useful as an educational tool and they help develop deeper physical understanding than numerical simulations.

While there is relatively abundant literature on CubeSat thermal modeling, it appears that a compact reference appropriate for undergraduate and graduate students entering this field, and supported by easy to use open source code, has not been published yet. This paper is attempting to fill this gap and it is a result of our work with two CubeSat projects: the SOC-i satellite project³ at the University of Washington and the Perun satellite project4⁴ in Croatia.

A simple model for the satellite temperature variation with time can be derived by assuming that a single temperature applies to the entire satellite body at any given time. An implication of this assumption is that the thermal resistivity across the surface is vanishing and thus the entire surface can reach the same temperature very quickly (under a minute or less). This model permits an analytic solution when subjected to a bistable heat source with two segments that each have constant input power (the sum of input heating flux and internal power dissipation). A bistable heat source is a good approximation for a satellite orbit with an eclipsed segment when the Sun is not directly visible. The governing equations for such a simple model with bistable heat source are presented in the following Section, and numerical results are discussed in Section 5. In Section 6 we discuss active temperature control and summarize our conclusions in Section 7.

¹For more details and references, see https://en.wikipedia.org/wiki/CubeSat

²See https://en.wikipedia.org/wiki/List of CubeSats

³https://www.aa.washington.edu/news/article/2019-02-11/cubesat-team

⁴https://perun-i.hr/en/

Consider a satellite with a given geometry and assume a uniform temperature over its surface at any given time,

T(t). The temperature variation with time depends on the difference between heat source, Q_in, and heat sink, Q_out,

$mC\frac{dT}{dt}=Q_{in}-Q_{out}$   (1)

where m is the satellite mass and C is the material heat capacity. The heat capacity for most common materials used in satellites is listed in Table 1. The mC product is often called the thermal inertia. Heat sources and sinks are measured in Watts (W = Js^-1).

Radiative heat sink

Assuming that the satellite is in vacuum, the heat sink is due to radiative losses

$Q_{out}=A_{tot}{\in }_T\sigma T^4$   (2)

where A_tot is the satellite total surface area (e.g., for a spherical satellite A_tot = 4πR², where R is the satellite radius), σ = 5:67×10^-8 Wm^-2K^-4 is the Stefan-Boltzmann constant, and ϵ_T is the wavelength-averaged surface emissivity over the thermal flux distribution. The surface emissivity ϵ_T is approximately equal to the emissivity at the wavelength of the peak emission. From Wien's law, this wavelength is equal to (3000 Kμm)/T and thus for T ≈ 300 K, ϵ_T is approximately equal to the material emissivity around 10μm. Typical values of ϵ_T for materials used in satellite industry are in the range 0.8-0.9; values of ϵ_T for common materials are listed in Table 4.

The energy spent on battery charging (the conversion of incoming solar flux to chemical energy) is also a heat sink. However, essentially all of that energy is returned back as a heat source at a later time. The treatment of these effects is discussed separately further below.

Heat sources

The heat sources can include direct solar radiation, Q_sun, solar radiation reected from Earth, Q_ref, and thermal infrared emission from Earth, Q_IR. When the satellite is exposed to direct sunlight, the maximum possible heat source corresponds to

$Q_{in}^{sun}=Q_{sun}+Q_{ref}+Q_{IR}$   (3)

while the minimum possible heating corresponds to

$Q_{in}^{eclipse}=Q_{IR}$   (4)

when the satellite is in Earth's shadow (eclipsed by Earth). For illustration, see Figure 1.

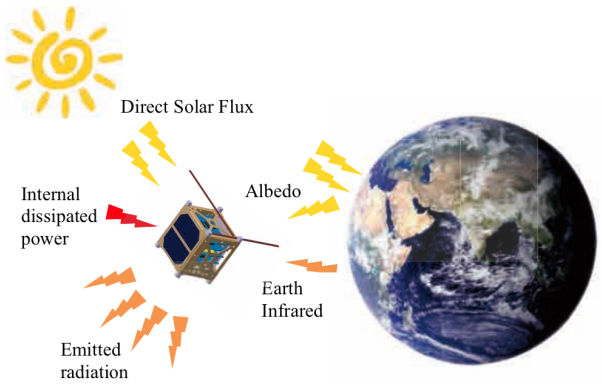
Figure 1 An illustration of the satellite heat balance (here 1U CubeSat satellite is shown). The heat sources include direct solar radiation, solar radiation reflected from Earth (albedo), infrared radiation emitted by Earth, and internally dissipated power. Conversion of input radiation to chemical energy in batteries is not shown. The heat sink is thermal infrared radiation emitted by the satellite and energy for battery charging. Credit: Figure 2.2 from the master thesis by Lionel Jacques (2009, University of Liege).

Solar radiation

The time-averaged solar flux is about F_sun=1372 Wm^-2 and its spectral energy distribution peaks at wavelengths of about 0.5μm (yellow light; the Sun's surface temperature is about 5,800 K). Since Earth's orbit is not circular, the solar flux varies from 1322 Wm^-2 in June to 1422 Wm^-2 in December, or by about 4% around its mean value (see Table 3). The absorbed energy due to solar flux is then (Gilmore 2002)

$Q_{sun}=A_S{\alpha }_S{F}_{sun}={\eta }_S{A}_{tot}{\alpha }_S{F}_{sun}$   (5)

where A_S is the satellite's mean projected surface area towards the Sun (for sphere, A_S = πR² and η_S = 1/4), and α_S is the wavelength-averaged surface absorptivity over the solar flux distribution. Following Kirchhoff's law, absorptivity α_S is approximately equal to the emissivity at 0.5μm, the wavelength of the peak of the solar spectral energy distribution.⁵ The low values of α_S imply high reflectivity and ”shiny" surfaces. The values of α_S for common materials are listed in Table 4.

Solar radiation reflected from Earth

The fraction of solar flux reflected by Earth back towards the satellite is typically ρ_E = 0.3, and it varies in the

range ρ_E = 0.2-0.4 across Earths' surface and oceans. The reflected flux depends on the "Sun-Earth-satellite" angle, θ, and it is maximized when the satellite is at the subsolar point. Gilmore (2002) gives an approximate formula for the variation of reflected light with θ as

$f(\theta )={\left[\cos \left(0.9\theta \right)\right]}^{1.5}$   (6)

that can be used to derive mean correction, f_alb, for a given orbit. For example, for a polar orbit passing through

subsolar point, f_alb = 0.62 for the non-eclipsed part of the orbit, and for a polar orbit perpendicular to it (with θ = 90 deg. and no eclipsed part), f_alb = 0.06.

The absorbed energy from the reflected solar radiation is then (Gilmore 2002)

$Q_{ref}=f_E{A}_E{f}_{alb}{\rho }_E{\alpha }_S{F}_{sun}=f_E{\eta }_E{A}_{tot}{f}_{alb}{\rho }_E{\alpha }_S{F}_{sun}$   (7)

where A_E is the satellite's effective projected surface area towards Earth. The f_E factor accounts for the fact that

Earth fills less than 2π srad (\half the sky") as viewed from the satellite, and is defined as (Gilmore 2002)

$f_E={\left(\frac{R_E}{R_E+h}\right)}^2$   (8)

where R_E = 6, 378 km is the Earth's mean radius and h is the satellite's altitude (typically, h = 550 km for a low-Earth orbit, giving f_E ~ 0.85). The ratio η_E = A_E/A_tot needs to account for the fact that incoming radiation from Earth is not plane-parallel as is the case for direct solar radiation. The computation of η_E is based on the concept of radiative viewing factors and it is discussed in more detail in Appendix A. The resulting η_E for spherical and CubeSat satellites are further discussed in 4.4.

Therefore,

$Q_{ref}=f_E\frac{{\eta }_E}{{\eta }_S}{f}_{alb}{\rho }_E{Q}_{sun}$   (9)

Infrared radiation emitted by Earth

The thermal infrared flux emitted by Earth is about F_IR=240 Wm^-2 on average (see Table 3), and it is equal to one quarter (the ratio A_S/A_tot for Earth) of the absorbed solar radiation (for ρ_E = 0.3, 70% of F_sun is absorbed by Earth). Since Earth's equilibrium temperature of ≈300 K, the spectral energy distribution of this radiation peaks at about 10μm. Therefore,

$Q_{IR}=f_E{A}_E{\alpha }_{IR}{F}_{IR}=f_E{\eta }_E{A}_{tot}{\alpha }_{IR}{F}_{IR}$   (10)

where α_IR is the wavelength-averaged surface absorptivity over the Earth's thermal flux distribution. Given Kirchhoff's law and the fact that the satellite and Earth's temperatures are similar, α_IR ≈ ϵ_T. Due to varying emission properties of Earth's surface (oceans, continents, clouds), FIR can vary by about ±10% along the satellite's orbit.

Internal power dissipation

A fraction of absorbed optical flux (the sum of Q_sun and Q_ref ) is often used to charge on-board batteries. Upto about 30% of absorbed flux can be thus converted into chemical energy. This energy conversion is also a heat sink. However, essentially all of that energy is returned back as a heat source at a later time (except for a small fraction needed to power on-board computer and to emit communication signal back to Earth), motivating a separate treatment.

The energy stored in batteries can be dissipated in various ways, including at a constant rate and in short bursts.

Here it will be assumed that batteries are charged using 30% of absorbed flux (solar cell efficiency η_cell = 0.3) during non-eclipsed portion of the orbit, and that this accumulated energy is dissipated at a constant rate during the entire orbit. If fraction η_P of the orbital period P is spent in Earth's shadow, then eqs. 3 and 4 have to be modified as

$Q_{in}^{sun}=\left(1-{\eta }_P\ast {\eta }_{cell}\right)\ast \left(Q_{sun}+Q_{ref}\right)++Q_{IR}$   (11)

and

$Q_{in}^{eclipse}=Q_{IR}+{\eta }_{cell}\left(1-{\eta }_P\right)\left(Q_{sun}+Q_{ref}\right)$   (12)

where the second term in eq. 12 is the battery power internally dissipated as heat at a constant rate during the entire orbit,

$Q_{dissip}={\eta }_{cell}\left(1-{\eta }_P\right)\left(Q_{sun}+Q_{ref}\right)$   (13)

Of course, eqs. 3 and 4 are recovered when η_cell = 0. Finally, it is good to emphasize that η_cell represents the fraction of all absorbed radiation that was converted to battery charge. For example, if the cells occupy 2/3 of all external surfaces, and the cell conversion efficiency is 30%, then η_cell = 0.2. For randomized orientiations, it's only “effective" quantities that count in the model considered here; however, when a specific satellite orientation is known, one could incorporate information about where exactly the solar cell panels are positioned, too.

Effective surface areas A_S and A_E for 1U and 2U CubeSat satellites

Three surface areas matter for heat balance:

• The total surface area, A_tot, that controls infrared radiation emitted by the satellite.
• The satellite projected surface area as viewed from the direction of incoming solar radiation, A_S = η_SA_tot. For example, η_S = 1/4 in case of spherical satellites.
• The projected surface area as viewed from Earth, with satellite in zenith, A_E = η_EA_tot. In more detail, the computation of A_E is a bit more complicated than in case of A_S because Earth is much closer than the Sun and it fills a much larger solid angle on the sky (e.g., in case of a spherical satellite very close to Earth, η_S = 1/4 and η_E = 1/2, while asymptotically η_E = 1/4 when the satellite is much further away; for an orbit altitude of 550km, η_E = 0.36).

In case of non-spherical satellites, the satellite orientation matters. For a given orientation and CubeSat satellites, η_S and η_E can be computed by adding values for six individual sides, which are computed as discussed in Appendix A. When averaged over plausible orientations and orbits, for 1U and 2U CubeSat geometries η_S = 0:21 and η_E = 0.36, with a plausible uncertainty due to actual orbit specifics of the order 10%. Given that equilibrium temperature is proportional to η^1/4 (see eq. 14 below), the implied temperature uncertainty due to 10% uncertainties in η factors is about 2.5%, or about 7ºC assuming a typical temperature of 273 K.

For an orbit altitude of 550 km, for a spherical satellite η_S = 0:25 and η_E = 0:36, while for a 2U CubeSat η_S≈ 0.21 and η_E ≈ 0.36. Therefore, given everything else same, the equilibrium temperature for the spherical satellite will be slightly higher (typically of the order 10ºC) than for the CubeSat because of 20% higher absorbed direct solar radiation.

Typical numerical values of heat sources and sinks for 2U CubeSat

A “randomly oriented" 2U CubeSat is used for numerical analysis and illustration, with A_tot = 0.1 m², η_S = 0.21,

and η_E = 0.36. Numerical input assumptions include mean environmental parameters from Table 3, aluminum heat capacity C = 921 J kg^-1 K^-1, satellite mass m = 2.0kg, surfaces with α_S = 0.86 and ϵ_T = 0.86 (black anodized aluminum), η_cell = 0.2, and a Sun-synchronous orbit with h = 550 km (assumed orbital period of 90 minutes), with η_P = 0.33 and f_alb = 0.62. Note that these parameters do not correspond to any particular satellite.

With these input parameters, $Q_{in}^{sun}$  =40.1 W and $Q_{in}^{eclipse}$ =11.1 W, with absorbed direct solar radiation Q_sun=29.5 W, and with dissipated thermal power contributing a constant rate of Q_dissip =4.8 W. Absorbed direct solar radiation is about five times as large as absorbed reflected solar radiation, and larger by a similar factor than absorbed Earth's infrared emission. The total battery energy charged and then dissipated during one orbital period is 7.2 Wh.

High and low equilibrium temperatures

The equilibrium temperature can be computed by assuming that the satellite is exposed to a constant heat source

for an infinitely long time and thus dT/dt = 0. It then follows from eqs. 1 and 2 that

$T_{eq}={\left(\frac{Q_{in}}{A_{tot}{\in }_T\sigma }\right)}^{1/4}$   (14)

Note that the equilibrium temperature does not depend on satellite's thermal inertia (the product of mass and heat capacity). Because for a given geometry and orientation Q_in is proportional to the total area A_tot, the equilibrium temperature does not depend on satellite's size either.

Assuming $Q_{in}^{sun}$  =40.1 W and $Q_{in}^{eclipse}$  =11.1 W, the corresponding equilibrium temperatures are $T_{eq}^{sun}$  = 301.1 K

(27.9 ºC) and $T_{eq}^{eclipse}$ = 218.6 K (-54.6ºC). This temperature range is much larger than satellite temperature variation expected for oscillatory heating in a typical orbit, as discussed next.

Analytic solution for the temperature's return to its equilibrium value

Equation 1 is typically solved using numerical integration. When the heat source is constant in time, the solution can be obtained analytically. Equation 1 can be recast using eqs. 2 and 14 as

$\frac{d\tau }{dx}=1-{\tau }^4$   (15)

where τ = T/T_eq, x = t/t_o and the time scale t_o is given by

$t_o=\frac{Cm}{A_{tot}{\in }_T\sigma T_{eq}^3}$   (16)

The derivative dτ/dx is positive when starting temperature T_o = T(t = 0) is T_o < T_eq. Thus, when Q_in =$Q_{in}^{sun}$  and T_eq = $T_{eq}^{sun}$ , the temperature will be increasing with time, while for Q_in = $Q_{in}^{eclipse}$  and Teq = $T_{eq}^{eclipse}$  the derivative is negative and the temperature decreases with time.

The simplified dimensionless differential equation 15 admits an implicit analytic solution:

$\frac{t}{t_o}=\frac{1}{2}\left[\arctan \left(\tau \right)-\arctan \left({\tau }_o\right)\right]+\frac{1}{4}\left[\ln \left(\frac{\tau +1}{{\tau }_o+1}\right)-\ln \left(\frac{\tau -1}{{\tau }_o-1}\right)\right]$   (17)

where τ_o = T_o=T_eq is the initial condition. When t » t_o, τ asymptotically approaches unity. Figure 2 illustrates solutions given by eq. 17 for both τ_o < 1 and τ_o > 1.

Figure 2 The analytic solution for dimensionless temperature parameter τ(t) = T(t)/T_eq as a function of dimensionless time parameter t/t_o for initial conditions with τ_o < 1 (left) and τ_o > 1 (right). Note that in both cases τ(t) asymptotically approaches unity, that is, T(t) asymptotically approaches T_eq.

Temperature variation for a bistable heat source

Now consider a bistable heat source, such as a satellite in an orbit and the heat source periodically switching between $Q_{in}^{sun}$ and $Q_{in}^{eclipse}$ . Because corresponding equilibrium temperatures $T_{eq}^{sun}$ and $T_{eq}^{eclipse}$ are different, the implied time scales for the temperature's return to its equilibrium value, to given by eq. 16, will be different, too. Eq. 16 implies that the ratio of time scales in eclipse and when exposed to sunlight is

$\frac{t_o^{eclipse}}{t_o^{sun}}={\left(\frac{Q_{in}^{sun}}{Q_{in}^{eclipse}}\right)}^{3/4}\approx 3$   (18)

For a bistable heat source, the temperature at the end of the rising phase must be equal to the temperature at the start of cooling phase and vice versa. As a result of this condition, the temperature will oscillate between two extremes, T_min and T_max with T_min ≥ $T_{eq}^{eclipse}$ and T_max ≥ $T_{eq}^{sun}$ . Eq. 17 appears too cumbersome to derive closed-form analytic solutions for T_min and T_max; in practice, T_min and T_max are easily determined numerically (see Appendix B).

When thermal inertia is vanishing, the temperature will return to its equilibrium values essentially instantaneously and most of the time the satellite temperature will be either $T_{eq}^{eclipse}$ or $T_{eq}^{sun}$ . On the other hand, for infinitely large thermal inertia the temperature will assume an equilibrium value that corresponds to the heat source averaged over the satellite orbit. For example, if the satellite spends one third of the orbital period in eclipse, then

$T_{eq}^{ave}={\left[\frac{1}{3}{\left(T_{eq}^{eclipse}\right)}^4+\frac{2}{3}{\left(T_{eq}^{sun}\right)}^4\right]}^{1/4}$   (19)

With $T_{eq}^{sun}$ = 301.1 K and $T_{eq}^{eclipse}$  = 218.6 K, $T_{eq}^{ave}$ = 281.1 K (7.9ºC). With thermal inertia corresponding to heat capacity for aluminum (C = 921 J kg^-1 K^-1, see Table 1), and satellite mass m = 2.0kg, the actual temperature extremes are T_min = 272.4 K (-0.8ºC) and T_max = 289.1 K (16.0ºC). Note that the T_max-T_min difference is about five times smaller than the $T_{eq}^{sun}-T_{eq}^{eclipse}$ difference. The variation of these extreme orbital temperatures on various input parameters is discussed next.

⁵The following convention is used in ESA and NASA literature: ϵ is the mean emissivity (and absorptivity) in the infrared wavelength range (5-35μm), and α is the mean absorptivity (and emissivity) in the optical wavelength range (0.3-2.4μm).

This section explores the impact of variations in input parameters on the mean satellite temperature and the amplitude of temperature variations. The concept of hot and cold cases is also discussed. Note that numerical values of various parameters were chosen to be similar to 2U CubeSat parameters; however, they do not correspond to any particular satellite.

The impact of thermal inertia on the amplitude of temperature variation

Figure 3 shows the satellite orbital temperature variation as a function of the surface emissivity properties and thermal inertia. The temperature variation is computed using analytic solution given by eq. 17 and emissivity properties corresponding to three different types of anodized aluminum surfaces (see figure caption). It is assumed that the orbital period is 90 min, with the eclipse portion lasting 30 min. The aluminium heat capacity is assumed and the thermal inertia is controlled by the satellite mass.

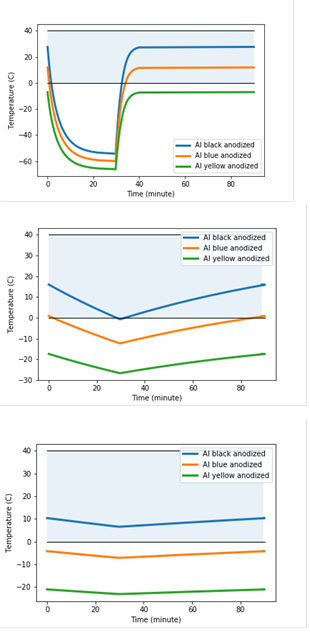
Figure 3 The satellite orbital temperature variation as a function of the surface emissivity properties and thermal inertia. The satellite total surface area is 0.1 m² (similar to 2U CubeSat), with effective absorptive surfaces corresponding to a spherical satellite. Three different types of anodized aluminum surfaces are modeled: black with α_S; ϵ_T = (0.86, 0.86), blue: (0.67, 0.87) and yellow: (0.47, 0.87). The thermal inertia is controlled by the satellite mass; left: low (0.05 kg), middle: medium (2.2kg), right: high (10 kg). The temperature variation is compared to a typical battery operating temperature range (the blue horizontal band).

For low thermal inertia (left panel), the temperature displays large variation, drops quickly to the cold equilibrium temperature and rises back even faster to the hot equilibrium temperature. For very high thermal inertia (right panel) the temperature varies by only a few degrees around the value given by eq. 19 (7.9ºC for black anodized Al surface). In the most realistic case shown in the middle panel, the temperature variation amplitude is 10-17 degrees, depending on the surface properties.

This behavior is similar to potatoes taken from a hot oven: small satellites would cool faster than their scaled-up larger versions. However, here the difference in behavior is due to different thermal inertia for satellites that look identical from the outside (same size, shape and surface properties). Instead of small and large potatoes, a better analogy is solid and hollow potatoes of the same size.

It is important to recognize that some components within the satellite could achieve temperatures higher than T_max (components close to the locations of internal power dissipation) but never lower than T_min (assuming steady-state after many cycles). To obtain temperature variation for individual components, a professional tool (e.g., Thermal Desktop, Ansys) and detailed numerical computations need to be employed. Nevertheless, the essential impact of thermal inertia on the amplitude of temperature variation will remain. Perhaps the most important conclusion of this simplified analysis that pertains to detailed numerical modeling is that a full transient model must be employed to assess the temperature variation between T_min and T_max. The extreme equilibrium temperatures, $T_{eq}^{sun}$ and $T_{eq}^{eclipse}$ are not representative of the actual temperature variation experienced by the satellite.

In practice, the uncertainty in thermal inertia is much smaller than discussed in Figure 3. The top left panel in Figure 4 shows that varying thermal inertia by ±30% around its mean value changes temperature predictions by about 5ºC.

The impact of variable solar flux on predicted satellite temperature

Due to Earth's elliptical orbit around the Sun, the solar flux at Earth's location varies by about 3.6% around its mean value, between its maximum at winter solstice and its minimum at summer solstice (see Table 3). The top right panel in Figure 4 shows that this variation changes the minimum and maximum temperatures by about 3-4 degrees.

The impact of battery charging on the amplitude of temperature variation

The energy spent to charge on-board batteries is converted to chemical energy and subtracted from heat balance (see eq. 1). It is returned to heat balance in the form of resistive heat dissipation, at a constant rate as assumed here. Because the charging does not happen during the eclipsed portion of the orbit, this dissipation effectively “flattens" the heat source variation and decreases the amplitude of temperature variation. The bottom left panel in Figure 4 shows that the conversion of 20% of incoming solar flux to battery charge and release as heat can decrease the amplitude of temperature variation by about 5 degrees compared to no-battery case.

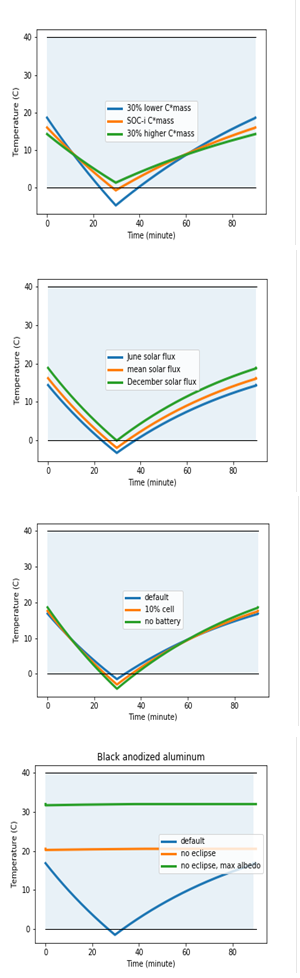
Figure 4 The impact of thermal inertia (top left), solar flux variation (top right), solar cell efficiency (bottom left) and the eclipse duration (bottom right) on satellite orbital temperature variation (all for black anodized aluminum surface with α_S; ϵ_T = 0.86, 0.86). In the bottom left panel, it is assumed that a fraction of absorbed solar radiation is used to charge batteries, and it is then dissipated as heat at a constant rate throughout the orbit. In the bottom right panel, the no eclipse case corresponds to a polar orbit whose normal vector points to the Sun. The effective albedo is varied from 0.06 times its maximum value, as expected for such an orbit, to 0.6 times its maximum value, as expected for an orbit that includes subsolar point. The temperature variation is compared to a typical battery operating temperature range (0-40ºC, the blue horizontal band).

The impact of eclipse duration on the amplitude of temperature variation

Given a fixed orbital period, the shorter is the eclipse the higher is the total accumulated energy. The bottom right panel in Figure 4 compares two polar orbits, one whose normal vector points to the Sun, with no eclipse, and another one that includes subsolar point and has one third of orbital period spent in eclipse. The impact on mean temperature is about 10-15 degrees. Uncertainties in effective albedo contribute to the uncertainty in predicted temperatures; when albedo is varied from 0.06 times its maximum value, as expected for the first orbit with no eclipse, to 0.6 times its maximum value, the temperature is raised by another 10 degrees.

The concept of hot and cold cases

Due to uncertainties in input parameters, including environmental, orbital and satellite parameters, engineering pre-launch analysis often focuses on the most extreme scenarios that predict the coldest and the hottest satellite temperatures.

The top left panel in Figure 5 compares the cold and hot cases for a spherical satellite, with the extreme values of environmental parameters taken from Table 3. The predicted temperature extremes differ by about 25 degrees. The top right panel in Figure 5 explores the impact of uncertainties in orbital parameters and satellite orientation by varying η_E by 20% around its mean value (about twice as much as typical uncertainties for a 2U CubeSat). The predicted temperature extremes differ by about 10 degrees.

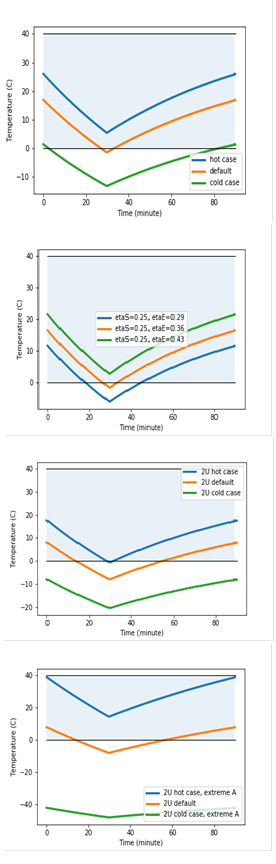
Figure 5 The impact of choosing extreme values of environmental conditions (top left), varying geometry expressed through 20% variation of the absorptive surface area (top right), extreme values of environmental conditions when assuming 2U CubeSat satellite geometry with randomized orientation (bottom left, η_S = 0:21 and η_E = 0:36), and with orientation that maximizes the temperature range between these so-called “hot" and “cold" cases (bottom right, hot: η_S = 0:30 and η_E = 0:38; cold: η_S = 0:10 and η_E = 0:34). The temperature variation is compared to a typical battery operating temperature range (the blue horizontal band).

The bottom left panel is analogous to the top left panel, except that typical values of η_S and η_E for 2U CubeSat are used instead of values for a spherical satellite. Note that these parameters do not correspond to any particular satellite. As expected, the predicted temperatures are about 8ºC higher for the spherical satellite because of higher absorbed direct solar radiation.

The bottom right panel in Figure 5 pushes the comparison of hot and cold cases for 2U CubeSat to its extreme. It is assumed that for hot case the satellite orientation is actively controlled so that during non-eclipsed portion its maximum possible projected area is always pointing towards the Sun, while during the eclipse it's pointed towards Earth (see figure caption). For cold case, the projected areas towards the Sun and Earth are minimized. The resulting temperature extremes differ by as much as 80 degrees. It is noteworthy that it is possible to reverse this scenario. If the satellite orientation is such that the projected areas are minimized for hot case, and maximized for cold case, the impact of environmental parameters can be reversed and hot case can be made colder than cold case. In other words, the satellite orientation can be more important than the variation of environmental parameters.

Given the allowed operating temperature ranges for satellite components (the most stringent requirement comes from batteries, chosen here as 0-40ºC for illustration), these results imply that low temperatures will be more worrisome than high temperatures. Motivated by this finding, we explored a model for active temperature control. As a concrete satellite example, we used SOC-i CubeSat developed at the University of Washington. Adopted parameter values are discussed and listed in Appendix D.

A toy model for active temperature control

A toy model for active temperature control that assumes an additional internal power dissipation whenever the satellite temperature drops below a pre-defined threshold is also developed. Analytic solution given by eq. 17 is not applicable any more because the time dependence of heat source is now an unspecified function and numerical integration is used to obtain the solution.⁶ Analytic solution given by eq. 17 was used to validate the numerical solution code in case of bistable heat source.

Cold case and three levels of power (2 W, 5, W, 10 W) that is applied whenever the temperature drops below 273 K (ºC) are investigated. Results are shown in figure 6. The consumed power is about 1.9 Wh, 3.4 Wh and 4.3 Wh, respectively (the total available battery power is 5.6 Wh). Additional power can raise the satellite temperature by 5 to 11 degrees. The consumed power ranges from 1.9 Wh to 4.3 Wh, and it is under the total available battery power (5.6 Wh for cold case and η_cell = 0.2; for hot, extreme case, it could be boosted to 18 Wh with η_cell = 0.3). These results show that such an approach is a viable method for mitigating low temperatures.

⁶Python code and Jupyter notebooks are publicly available at https://github.com/ivezic/CubeSats

When a body assumed to have a uniform temperature field is subjected to a bistable heat source, there exists an analytic solution for the temperature variation with time. This simplified model is suitable for addressing a variety of satellite thermal analysis problems: studying the relative effects of surfaces with different emissivities, the effects of small changes in the solar flux between June and December, the impact of thermal inertia on predicted amplitude of temperature variation, and as a \sanity check" for the results obtained with numerical thermal models that utilize detailed geometrical and thermal descriptions of all satellite components.

Brief examples of such studies are presented here. The most notable conclusions for further, more detailed studies with numerical tools, include:

• The mean satellite temperature depends on the extreme values of steady-state equilibrium temperatures for eclipsed and non-eclipsed parts of the orbit, and the duration of the eclipse relative to the orbital period (see eq. 19).
• The amplitude of temperature variation around the mean temperature is by and large controlled by the satellite thermal inertia (see Figure 3).
• Although one might naively think that the satellite temperature is lower during the eclipse than when the satellite is exposed to direct sunlight, the satellite temperature range is approximately identical for these two orbital phases because of cyclic boundary condition (unless the thermal inertia is unrealistically low). In other words, the temperature is at its maximum value just before entering the eclipsed portion of the orbit and at its minimum value just before exiting the eclipsed portion. The range of temperatures is thus the same for both eclipsed and non-eclipsed part of the orbit. When thermal inertia is sufficiently large to produce nearly linear temperature variation with time, the average temperatures are about the same, too.
• Satellites with non-spherical geometry can be modeled within the same framework with judiciously chosen effective surface areas, parametrized with η_S and η_E (see eq. 5 and Appendix A).
• For non-spherical satellites, such as 2U CubeSat, the satellite orientation can have a significant impact on the predicted temperatures; indeed, with active 2U CubeSat orientation control, the impact of environmental variations could be mitigated entirely (i.e., \hot case" achieving lower temperatures than “cold case").
• Model uncertainties, including uncertainties in input parameters, result in uncertainties of predicted temperatures of at least 10ºC!

Since it appeared that low temperatures will be more concerning than high temperatures, we also explored a toy model for active temperature control that assumes an additional internal power dissipation whenever the satellite temperature drops below a pre-defined threshold. It was found out that such an approach is a viable method for mitigating low temperatures. The latex source for this document, and the supporting python code for evaluating analytic and numerical models and producing all the plots presented here, are publicly available.⁷

⁷https://github.com/ivezic/CubeSats

An initial version of the code for obtaining a numerical solution of the differential equation 1 was contributed by Haley Stewart (University of Washington). I thank the University of Washington SOC-i team, in particular Boone Tate, Henry Brown and Charlie Kelly, for access to technical parameters describing their 2U CubeSat named SOC-i. Without seeing their enthusiasm, I would have never written this paper. I am also indebted to the members of the Croatian PERUN CubeSat project, in particular to Danko Bosanac, Zdenko Uvalic, Stjepan Puljic, Luka Orsag and Matija Makoter.

Author declares that there is no conflict of interest.

1. Effective area for the absorption of radiation from Earth

Effective area for the absorption of radiation from Earth can be computed using geometric radiative viewing factors (and remembering that the factor f_E is explicitly included in eq. 7).

For a spherical satellite,

${\eta }_E=\frac{1}{2}\left(1-\sqrt{1-f_E}\right)f_E^{-1}$   (1)

where f_E = [R_E=(R_E + h)]², with Earth's radius R_E = 6; 378 km and h is the satellite's altitude. As h increases, η_E for sphere varies from 1/2 to 1/4; for h = 550 km, η_E = 0:36.

For CubeSat satellites, η_E can be obtained as the sum of values for all 6 sides because the viewing factors are additive. For a at surface whose normal is at angle β relative to Earth's surface,

${\eta }_E=\cos \left(\beta \right)$   (2)

for $\left|\beta \right|\le$ arccos ($\sqrt{f_E}$ ), and otherwise

${\eta }_E={\pi }^{-1}\left[\left(\cos \left(\beta \right)\arccos \left(y\right)-xz\sin \left(\beta \right)\right)+f_E^{-1}\arctan \left(x^{-1}y\sin \left(\beta \right)\right)\right]$   (3)

where $x=\sqrt{f_E^{-1}-1},y=-x\tan {\left(\beta \right)}^{-1}$ and $z=\sqrt{1-y^2}$ . The same expressions can be used to compute η_S for CubeSat satellites by setting h to a very large value.

For randomly oriented CubeSat satellites, η_S ≈ 0:21 and η_E ≈ 0:36 for both 1U and 2U versions, with a scatter of about 10% around these mean values for realistic orientations. For 2U CubeSat with h = 550 km, the possible ranges are η_S = 0:10 - 0:30 and η_E = 0:34 - 0:38.

2. A method for enforcing cyclic boundary condition for equation 1

Given the orbital period and eclipse duration, two cooling time scales t_o (see eq. 16) and two steady-state equilibrium temperatures $T_{eq}^{sun}$ and $T_{eq}^{eclipse}$ , there are four unknowns to be solved for: ${\tau }_o^C,{\tau }_f^C,{\tau }_o^H$ and ${\tau }_f^H$ , where $\tau =\raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$T_{eq}$}\right.$ , subscripts o and f correspond to the initial and final values, and superscripts C and H correspond to eclipsed and non-eclipsed parts of the orbit.

Two equations come from the cyclic boundary condition that the final temperature for the C phase must be equal to the initial temperature for the H phase, and vice versa

${\tau }_o^H=C_1{\tau }_f^{C}and{\tau }_f^H=C_1{\tau }_o^C$   (4)

where $C_1=T_{eq}^{eclipse}/T_{eq}^{sun}\le 1$ . The remaining two equations come from applying eq. 17 to C and H phases, where the left side is known and the right hand side involves ${\tau }_o^C,{\tau }_f^C,{\tau }_o^H$ and ${\tau }_f^H$ , respectively.

After substituting eqs. 4 into two eqs. 17, the resulting system of two equations with two unknowns is easily solved numerically. In case of numerical solution for an arbitrary time dependence of the heating source, the cyclic boundary condition is satisfied using iterations (usually only a few iterations are sufficient).

3. Model parameters for the University of Washington SOC-i CubeSat

The University of Washington SOC-i⁸ (the Satellite for Optimal Control and Imaging) project⁹ has a specific mission to demonstrate the ability to satisfy two constraints with its orientation control and imaging systems. It was selected by NASA CubeSat Launch Initiative for launch in 2022 or 2023. We use it here as a specific example to quantitatively demonstrate the impact of active temperature control on the satellite's minimum temperature.

Input satellite parameters

We used the SOC-i CAD model¹⁰ developed for structural analysis to extract information about external satellite surfaces and their material properties. We adopted the following description of external SOC-i surfaces:

• Top: 60% solar panel, 40% aluminum frame
• Bottom: 38% aluminum frame, 62% PCB (printed circuit board).
• Sides (2): 64% solar panels, 19% aluminum panels (outside), 17% aluminum frame rails
• Sides (2): 57% solar panels, 26% aluminum panels (outside), 17% aluminum frame rails

With the values of absorptivity and emissivity listed in Table 4, we obtained their surface-weighted values α = 0.83 and ϵ = 0.79 (54% of external surface area is covered by solar panels). In addition, we assumed that the satellite mass is m = 2.6kg and adopted specific heat corresponding to aluminum (C = 768 J kg^-1 K^-1), yielding a thermal intertia of mC = 2.00 kJK^-1 (we note that a more accurate value of thermal inertia can be obtained by summing the mC product for all individual structural components in the SOC-i CAD model).

Assumptions for orbital parameters

It is already known that SOC-i will have a nearly-polar sun-synchronous orbit¹¹ with an altitude of h = 550 km and orbital inclination of 97.7 degrees. A satellite in sun-synchronous orbit passes over any given point of the planet's surface at the same local mean solar time because the orbit precesses through one complete revolution each year (that is, the orbit always maintains the same relationship with the Sun). The eclipse duration for sun-synchronous orbits depends on their right ascension of the ascending node (RAAN), which will not be known until the launch date (RAAN is determined by the exact launch time). The orbital period for sun-synchronous orbit with an altitude of h = 550 km is 96 mins, and the maximum eclipse duration is 36 mins. When the orbital plane is perpendicular to incoming solar radiation, there is no eclipse (the satellite is following the terminator line at all times).

Hot and cold cases

We define “hot" and “cold" cases by first adopting the extreme values of environmental parameters from Table 3. In addition, we make an assumption that the orientation of SOC-i's sun-synchronous orbit results in an eclipse with maximum duration (36 min) for cold case, and no eclipse at all for hot case. The intensity of solar radiation reflected from Earth varies along the orbit. For a polar orbit passing through subsolar point, f_alb = 0.62 for the non-eclipsed part of the orbit, while for a polar orbit aligned with the terminator (with no eclipse), f_alb = 0.06. Therefore, we adopt f_alb = 0.62 for hot case and f_alb = 0.06 for cold case (note that reflected solar radiation contributes more flux for cold case, when not in eclipse).

With these assumptions, we compute incoming heating flux. For cold case, the only heating flux during the eclipsed portion of the orbit is IR flux from Earth. The variation of flux between hot and cold cases for three main heat sources is summarized in Table 5. Note that reflected solar flux is smaller for hot case but this difference is compensated by the absence of eclipsed orbital portion in hot case.

Table 5 lists absorbed flux per unit area, assuming SOC-i's effective absorption coefficient (α). The listed value are also appropriate for detailed Ansys-based modeling, but need to be corrected for α of each surface material. The actual absorbed power (absorbed energy per unit time) depends on the values of η_S and η_E, which in turn depend on orientation. We make additional assumptions about satellite orientation, as discussed next.

Assumptions for satellite orientation

The satellite orientation determines effective surface areas for the absorption of radiation from the Sun and Earth. For convenience, these surface areas are expressed relative to the total surface area, A_tot (=0.1 m² for SOC-i), using η factors (ηS and ηE, respectively). We used results discussed in Section 2.4 to adopt the following values for SOC-i. When averaged over plausible orientations and orbits, η_S = 0.21 and η_E = 0.36, with an uncertainty due to actual orbit specifics of the order 10%. The limits of possible ranges are η_S = 0.10 – 0.30 and η_E = 0.34 – 0.38. The limits for η_S reflect the range of projected area towards plane-parallel rays for 2U CubeSat geometry, with the minimum value corresponding to one small side oriented perpendicularly to the incoming solar radiation. For η_E, the variation is much smaller because typically all six sides can “see" Earth's surface¹².

We do not adopt specific satellite orientation for hot and cold cases but instead explore two options in each case.

First, we adopt averaged orientations for both hot and cold cases, with η_S = 0.21 and η_E = 0.36 corresponding to 2U CubeSat values. As the second assumption, we consider the following extreme cases: η_S = 0.30 and η_E = 0.34 for hot case, and η_S = 0.10 and η_E = 0.38 for cold case. The second set of values assumes that the satellite orientation is actively controlled. For hot case, the maximum possible projected satellite area for plane-parallel rays is always pointing towards the Sun (η_S = 0.30). For cold case and during non-eclipsed portion, the smallest satellite side is always pointing towards the Sun (η_S = 0.10). The adopted values of η_E are its extreme values.

Assumptions for internal power dissipation

A fraction of absorbed optical flux (the sum of direct solar flux and reflected solar flux) is often used to charge

on-board batteries. We assume that 20% of absorbed flux¹³ is converted into chemical energy (η_cell = 0.2). This energy is returned back at a constant rate as internal heat dissipation. In hot case, satellite is always exposed to the Sun and there is no net effect within the context of single-temperature model considered here. In reality, and in detailed Ansys models, this internal heat dissipation can modify the temperature distribution within the satellite (areas closer to the heater will have elevated temperature). In cold case, the effect of internal heat dissipation is to minimize the amplitude of temperature variation, or equivalently, to raise the minimum temperature (at the end of eclipsed portion). These assumptions complete the specification of SOC-i hot and cold thermal models.

Predicted absorbed power and equilibrium temperatures for hot and cold cases

Given all the input assumptions described above, it is straightforward to solve the governing equation with direct numerical integration. Table 6 lists predicted absorbed power for all four modeled cases. We note that the total energy stored in batteries, and dissipated as heat at a constant rate, ranges from 3.2 Wh for cold, extreme case to 12 Wh for hot, extreme case.

⁸A nod toward the Pacific Northwest salmon.

⁹https://www.aa.washington.edu/news/article/2019-02-11/cubesat-team

¹⁰I am grateful to Boone Tate for extracting the model parameters.

¹¹See https://en.wikipedia.org/wiki/Sun-synchronous orbit

¹²We note that even for spherical geometry η_S and η_E are generally different: η_S = 1=4, while η_E decreases from 1/2 to 1/4 as the orbit altitude varies from zero to infinity.

¹³Here, η_cell represents the fraction of all absorbed radiation that was converted to battery charge. For example, if the cells occupy 2/3 of all external surfaces, and the cell conversion efficiency is 30%, then η_cell = 0.2. For randomized orientiations, it's only “effective" quantities that count in the model considered here; however, when a specific satellite orientation is known, one could incorporate information about where exactly the solar cell panels are positioned, too.

1. Gilmore D. Spacecraft Thermal Control Handbook: Fundamental Technologies. 2nd ed. Aerospace Press; 2002.
2. Jacques L. Thermal Design of the Oufti-1 Nanosatellite. Master Thesis, University of Liege; 2009.