This paper studies the effect of fatigue crack growth on the propagation characteristic of multi-frequency anti-symmetric Lamb wave modes in a C-Channel type aerospace structure through a Damage Response Factor (DRF) approach based on experimental testing with numerical verification. The approach is based on an algorithm for analyzing guided wave data excited at different frequencies, providing a method for identification of damage along an actuator-sensor path in a pitch-catch scenario. Computation of the DRF is based on the changes in the wave amplitude ratio, energy ratio, and cross correlation coefficient between the current and a baseline signal taken at the beginning of the test or at lowest load level. In addition to the commonly used threshold value, the DRF approach uses the upper and lower bounds on the average DRF value along with the separation of the DRF based on excitation frequency. By combining these criteria, a method for damage detection was developed. The approach presented here was experimentally and numerically verified for a C-Channel manufactured from aluminium alloy 7075-T651. A constant amplitude fatigue cyclic loading was applied to the C-Channel in order to grow a crack from a 3.2 mm diameter hole with a ~0.4 mm saw-cut starter notch. Multiple piezoelectric sensors were utilized to generate and capture a series of guided Lamb waves at different excitation frequencies to evaluate the presence of damage along each sensor path. Both the experimental measurements and the Finite Element Method (FEM) provide good agreement on the application of the DRF as a means for detecting damage. A “cycle-free baseline” damage detection method is also presented, which is based on interrogating the structure during the same cycle, but at different loading conditions.

Keywords: multi-frequency guided waves, structural health monitoring (SHM), damage detection, damage response factor (DRF), fatigue crack, cycle-free baseline

Many aircraft operators are seeking improvements to their aircraft fleet maintenance schedule by extending component life, increasing aircraft availability, and reducing the total life cycle costs. Extending the service life of a component often entails increasing the inspection requirement, which in turn increases the cost and reduces the aircraft availability. As the number of inspection/maintenance cycles is increased, there is always an increased risk for maintenance induced damage. In order to achieve these improvements while maintaining safety, Original Equipment Manufacturers (OEM), aircraft operators, and researchers are actively working on monitoring the condition of aircraft structural components using various load monitoring and Structural Health Monitoring (SHM) systems. Their common goal is to implement a Condition Based Maintenance (CBM) approach in order reduce operational costs. The definition of SHM in the context of this paper is adopted from MIL-STD-1530D as: “a nondestructive inspection process or technique that uses in-situ sensing devices to detect damage”.¹ In a typical SHM system, a structure is monitored continuously or at discrete intervals using advanced on-board sensors. Data gathered by the sensors can be processed on-board or sent to a ground control station for evaluation. The evaluation results are then used to identify damage occurrence and to inform the operator about the location, nature, and severity of the damage. Once these systems are proven reliable, SHM will aid in shifting from the current time / interval-based maintenance to Condition Based Maintenance (CBM), in which the aircraft is taken out of service only when maintenance and repair is required. Following such an approach will also reduce the costs associated with Non-Destructive Evaluation (NDE) and inspecting of damage prone areas that are difficult to access.

Even with increasingly sophisticated sensors and damage detection algorithms, Structural Health Monitoring (SHM) systems have not yet achieved widespread acceptance by aircraft operators. One of the challenges is the ability of SHM systems to provide robust damage detection algorithms to minimize/eliminate false-calls, which can prompt for unnecessary maintenance actions. Therefore, the primary objective of this study is to aid in reducing the false-call rates by using a newly developed Damage Response Factor (DRF) method. This method is based on the use of multi-frequency guided wave excitation for assessing the presence of damage along an actuator - sensor path. In this study, the corresponding change in the cross-correlation, amplitude ratio and energy ratio of the wave signal is analyzed to detect a growing fatigue crack in a C-Channel type structure. In addition to the commonly used threshold value, the DRF approach uses the upper and lower bounds of the average DRF value along with the separation of the DRF based on excitation frequency. The combination of all of these criteria, provide an improved means to identify damage in contrast to the classical sole-threshold method. This paper is an extension of the proceedings presented by the authors at the 9th European Workshop on Structural Health Monitoring (EWSHM) conference.² Therefore, information published in the EWSHM proceeding,² has been repeated here for completeness.

Concepts of Damage Index and Damage Matrix are not new. Ihn and Chang introduced Damage Index as the square root of the scatter energy of the So Lamb wave mode divided by the baseline energy of the So wave to correlate the sensor signal to the fatigue crack growth on a notched aluminium plate obtained from visual inspections.³ Giurgiutiu et al.,⁴ used a Damage Matrix concept based on the root mean squared and power deviation to study the effect of crack growth on Lamb wave transmission in an Arcan specimen with varying cross-section subjected to multi-mode fatigue loading. An increase in the Damage Matrix was observed with an increase in the crack length. Ryles et al.,⁵ used the Ao mode and Damage Index based on cross-correlation to detect change in frequency/phase due to crack growth in an aluminium plate undergoing fatigue loading and observed an increase in Damage Index with an increase in crack length; however, no alarm level (threshold value) was provided. These studies were done using a single excitation frequency. Multi-frequency analysis was performed by Lu et al. using the Finite Element Method (FEM) to study the interaction of transmitted and reflected So Lamb waves with frequencies ranging from 200 kHz to 600 kHz using dual-PZT (Lead Zirconate Titanate) sensors with a through-thickness crack in an aluminium plate by means of Hilbert Transform; only the 300 kHz wave was used for experimental verification. The authors observed no significant change in frequency in the reflection coefficient for relatively short crack lengths, defined in the paper as less than or equal to 40 mm, and found that the transmission coefficient values diverged at short crack lengths and converged as the crack lengths increased.⁶

The interaction of Lamb waves with fatigue crack opening and closing effect due to the differential loading was investigated by Pavelko et al. in an aluminium panel, where they found a significant decrease in Lamb wave amplitude (peak to peak voltage) in the loaded versus the unloaded state.⁷ Pavelko also used experimental and numerical techniques to study the interaction of Lamb waves excited at 250 kHz with the opening/closing effect of the fatigue crack due to differential loading on an aluminium panel. He found the presence of a threshold load above which the intensity of the transmitted signal did not change with increased loading.⁸ Lee et al. demonstrated both experimentally and theoretically the anisotropic effect (i.e. wave velocity as a function of the propagation angle) on the arrival times of various Lamb wave modes on an isotropic aluminium panel under various amounts of tensile load. They also noted that the time shift caused by the applied load was of the same order as that caused by the temperature change; however, the temperature change did not have the anisotropic effect.⁹ Gandhi et al. showed both theoretically and experimentally that the application of the tensile load had an anisotropic effect on an isotropic aluminium plate, which had a linear effect in Lamb wave phase velocity and sinusoidal dependence with angle of propagations at a single frequency; however, effects of crack were not included in this study.¹⁰ Gandhi’s results were corroborated by Boon et al.¹¹ Chen et al. used the load-differential technique in an aluminium plate, in which 100 kHz Ao Lamb wave signals obtained using multiple transducers at different loads under the same damage state were compared using delay-and-sum imaging techniques for detecting and visualizing crack locations.¹² In a later paper, Chen et al. extended the load-differential method from¹² and used minimum variance to find cracks emanating in aluminium plates from a hole with bolted and bonded doublers, and cracks emanating from multiple fastener holes. They were also able to discriminate between cracks from drilled holes and fastener tightness variation using this technique.¹³

Based on the current literature survey, it was found that most of the research regarding the effect of fatigue crack growth on Lamb wave propagation has been performed on flat, multi-layered and riveted plates using a single Lamb wave excitation frequency. Therefore, the objective of this paper is to study the effect of fatigue cracks on the propagation characteristics of multi-frequency guided wave mode in a C-Channel type structure. The novelty of the paper is the damage detection methodology based on the spread in the frequency response of the guided waves excited at different frequencies as a function of damage size. In addition, the methodology has been validated through the Finite Element Methods.

This study combines the effect of a growing fatigue crack and the multi-frequency propagation characteristics of the A₀ Lamb wave mode in a C-Channel structure made from aluminium alloy 7075-T651 shown in Figure 1.

Figure 1 Overall dimension of the C-Channel structure used in this study.

A 0.25 mm thick jeweller’s saw blade was used to introduce a saw-cut approximately 0.4 mm in length to act as a fatigue crack starter notch at the edge of the 3.2 mm diameter hole, shown as Detail A view in Figure 1. To grow the crack, the C-Channel was loaded in tension-tension fatigue using a sinusoidal waveform at a frequency of 2 Hz with a maximum load of 2500 lbf [11120 N] and a load ratio of R = 0.1. The crack was monitored using an AVT Dolphin F145b digital video camera. The camera was used to capture images at peak load, at the end of each block of 5000 cycles up to 40000 cycles, then at blocks of 3000 cycles up to 55000 cycles. This was done for detecting and measuring the crack length. The test setup is shown in Figure 2.

Figure 2 Fatigue crack growth test setup.

For exciting and acquiring the Lamb waves, commercially available piezoelectric Lead Zirconate Titanate (PZT) surface mount single sensors from Acellent Inc. were permanently bonded onto the C-Channel using M-Bond 200 adhesive. Four PZT sensors were used in total, two on the flange (PZT-1 and PZT-2) and two on the web (PZT-3 and PZT-4) of the C-Channel, exact locations are shown in Figure 3. The PZTs were connected to the ScanGenie hardware from Acellent Inc., which was controlled by custom software developed in Matlab. The custom software was used to excite and gather data from the PZT sensors. Data was gathered at the end of each block at 12 MS/s by exciting the installed PZTs at frequencies of 100 kHz and 200 kHz using a five-cycle Hanning-windowed sine-burst.

Figure 3 Location of PZT sensors within the C-Channel structure.

In order to perform the guided Lamb wave analysis, data was gathered at the end of each test block under no (zero) load, up to 55000 cycles. Five data sets were acquired for each run and were averaged for analysis. The averaged data at the end of each test block was compared against the baseline data acquired at the beginning of the test (0 cycles). Only the Ao Lamb wave mode was used for this study, where the analytical Lamb wave dispersion velocity and the Morlet Wavelet coefficients were used to find the arrival time and to isolate the corresponding Ao wave packet, as shown in Figure 4.

Figure 4 Extraction of the A₀ wave packet for analysis.

A two-step process was used to extract the Ao wave packet. In the first step, the Ao wave packet Time of Arrival (ToA) was estimated using the analytical dispersion data and the actuation signal, as shown by the vertical red dotted lines in Figure 4. In the second step, the actual arrival time of the Ao wave (within the estimated ToA window) was extracted. The windowed wave packet for the analysis was 200% of the actuation wave span, centered at the actual arrival time, as shown by the solid vertical black lines in Figure 4. The method for extracting the Ao wave packet differs in this work from what was presented in.² In this paper an improved automated method described in the previous sentence was used as compared to extracting the wave packet manually in.² 

Three parameters – Correlation Coefficient (CC), Energy Ratio (ER) and Amplitude Ratio (AR) were used for analysis. The correlation coefficient (measured between 0 and ±1) provided information regarding how close the waves acquired at different cycles were to the baseline (linear dependence). The Correlation Coefficient (CC) was calculated using the Matlab function (corrcoef), which is given as:¹⁴

$CC\left(x_i,x_0\right)=\frac{1}{m-1}{\displaystyle \sum _{n=1}^m\left(\frac{x_i\left(n\right)-u_{x_i}}{{\sigma }_{x_i}}\right)}\left(\frac{x_0\left(n\right)-u_{x_0}}{{\sigma }_{x_0}}\right)$ (1)

Where, m = number of samples, μ = mean, σ = standard deviation, x_i(n) and x₀(n) are the current and baseline signals respectively.

The Energy Ratio (ER) provided information regarding the loss of wave energy due to spreading around the crack and was calculated using:

$ER=\frac{{\displaystyle \sum _{n=1}^m{\left|x_i\left(n\right)\right|}^2}}{{\displaystyle \sum _{n=1}^m{\left|x_0\left(n\right)\right|}^2}}$ (2)

Where, m = number of samples, x_i(n) and x₀(n) are the current and baseline signals respectively. 

The Amplitude Ratio (AR) is calculated as the difference between maximum and minimum amplitude of the current wave divided by the difference between maximum and minimum amplitude of the baseline wave. The AR provided information regarding wave attenuation and scattering due to the presence of a growing crack and was calculated using:

$AR=\frac{\max (x_i)-\min (x_i)}{\max (x_0)-\min (x_0)}$ (3)

Where, x_i and x₀ are the current and baseline signals respectively.

The AR used here minimizes error due to any DC offset present in the signal; whereas in,¹ the AR was calculated as the absolute maximum amplitude of the current wave divided by the absolute maximum amplitude of the baseline wave.

Crack length measurement

The saw-cut area at the edge of the 3.2 mm diameter hole was monitored visually with the aid of an AVT Dolphin F145b digital video camera. At the end of each block, a tensile load was applied to the coupon up to a 100% of the maximum load of 2500 lbf [11120 N], in order to acquire images at a consistent load level. A clear indication of the crack emanating from the hole with the saw-cut was found at 35000 cycles, as shown in Figure 5.

Figure 5 Images of fatigue crack at different cycles.

The crack length was tracked using the ImageJ software,¹⁵ where the pixel distance of the crack was converted into an actual crack growth length. The resultant fatigue crack growth along with the measured strain close to the hole with the saw-cut is shown in Figure 6.

Figure 6 Fatigue crack growth and measured strain.

Strain data shown in Figure 6b was measured using a general purpose CAE-13-125UN-350 strain gauge from Micro-Measurements connected to a HBM QuantamX MX840 DAQ system, which was monitored through CATMAN AP software. From Figure 6, it can be observed that the there is an increase in the maximum strain value due to crack growth. It is to be noted that the crack length between 40000 cycles and 55000 cycles could not be measured visually using the camera because the crack was propagating underneath the installed cracK Indication Sensor (KIS),¹⁶ as shown in Figure 5. The KIS system was used to find the presence of a crack at a desired length, just in case the crack was not visible in the acquired digital images.

To extract the crack length at different cycle counts, an exponential trend line was fitted to the experimental crack growth data in Excel, as shown in Figure 6a. It is to be noted that the exponential trend line does not represent the exact crack growth behaviour; however, it was used to interpolate the crack growth data at different cycles for use in comparing experimental results against the FEM results.

Guided wave analysis–experimental results

The experimental results of Cross Correlation (CC), Energy Ratio (ER), and Amplitude Ratio (AR) analysis for the waves propagating between Actuator (Act) and Sensor (Sen) are shown in Figure 7-9, where actual data points are represented by markers that are connected with smooth lines. As discussed earlier, for brevity, only three major wave paths travelling between Act 1 to Sen 2, Act 1 to Sen 4, and Act 3 to Sen 4 are used for analysis.

Figure 7 Multi-frequency response at 0 lbf [0 N] for Act 1 - Sen 2 (in line with the damage site).

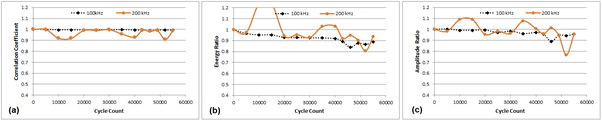
Figure 8 Multi-frequency response at 0 lbf [0 N] for Act 1 - Sen 4 (diagonal path to the damage site).

Figure 9 Multi-frequency response at 0 lbf [0 N] for Act 3 - Sen 4 (outside of the damage site).

From Figure 7, it can be observed that there is consistent reduction in CC, ER, and AR values for the wave propagating between Act 1 - Sen 2, which is in-line with the growing crack, as compared to Figure 8 and Figure 9 for all Act-Sen combinations that are not directly in-line with the crack (locations of PZT transducers are shown in Figure 3). From Figure 7, it can also be observed that ER is more responsive than CC and AR due to the presence of a growing crack.

In order to have a quantitative measure for crack detection using the traditional single frequency threshold technique, one needs three different threshold values to detect the presence of a growing crack if all CC, ER, and AR are to be used. Also probability of false calls for the single frequency threshold technique can be high. For example, if an arbitrary value of 0.9 is taken as a threshold value for CC, waves propagating between Act 1 - Sen 2 (Figure 7a), as well as Act 3 - Sen 4 (Figure 9a) do not show any signs of a crack being present within their paths for all excited frequencies, i.e., none of the CC responses are below the threshold value of 0.9. However, waves propagating between Act 1 - Sen 4 (Figure 8a) show signs of the existence of a crack at 50000 cycles when excited at 200 kHz, if the same 0.9 threshold value for CC is used. Furthermore, if the threshold value is reduced from 0.9 to 0.89, signs of a crack can be found as early as 10000 cycles for the same wave path propagating between Act 1 - Sen 4 (Figure 8a).

Similarly, if 0.89 is used as a threshold value for AR for Act 1 - Sen 2 (Figure 7c) corresponding to the presence of a 0.5 mm crack at 35000 cycles for the 100 kHz wave; at 46000 cycles the AR for Act 1 - Sen 4 (not directly in line with the crack) is below 0.89 for the same 100 kHz wave (Figure 8c). If AR with the threshold of 0.80 for a 200 kHz wave is used for Act 1 - Sen 2 (Figure 7c) corresponding to the presence of a 0.5 mm crack at 35000 cycles; the same response can be found for Act 1 - Sen 4 at 50000 cycles for a 200 kHz wave (Figure 8c). This emphasises the fact that a drop in the CC, ER, and AR parameters below a threshold value for a single frequency alone is not sufficient to guarantee the presence of a crack / damage and as such, is indicative of the need to analyze other trends in the data.

In response to this need, a novel method is presented in this paper, which is based on observing the trends of guided waves excited at multiple frequencies to witness how the waves with smaller wavelengths behave as compared to the waves of same mode but with longer wavelengths. Theoretically, the waves excited with smaller wavelengths (associated with higher frequency excitation) would be more reactive to the presence of damage as compared to the waves with longer wavelengths (associated with lower frequency excitation) for the same wave mode. This phenomenon can be observed in Figure 7, where the 200 kHz wave is found to be more responsive than the 100 kHz wave, which means there is a higher reduction in CC, ER and AR values at 200 kHz as compared to 100 kHz as the crack grows. The estimated half-wavelengths corresponding to the A₀ wave packets excited at 100 kHz and 200 kHz are 6.7 mm and 11 mm respectively.

Instead of using CC, ER, and, AR separately, the novel method proposed in this study combines them in a form of a Damage Response Factor (DRF), which is given as:

$DRF=\frac{\sqrt{C{C}^2+E{R}^2+A{R}^2}}{\sqrt{3}}$ (4)

DRF combines the three parameters commonly used for detecting damage as a Euclidian norm. The algorithm uses DRF calculated at different frequencies along with the threshold value and the spread in the frequency response for detecting damage and is described in Figure 10.

Figure 10 Damage detecting algorithm using the DRF.

The multi-frequency spread is the difference between the lowest and the highest frequency DRF values as calculated in Eqn. 5. The DRF is computed through Eqn. 4 for each excitated frequency.

$Spread=abs\left(DR{F}_{Lowest frequency}-DR{F}_{Highest frequency}\right)$ (5)

The upper and lower bounds are determined by the following equation at the selected threshold cycle and / or crack length.

$\begin{array}{l}Upper bound=abs(Average DRF-DR{F}_{Lowest frequency})\\ Lower bound=abs(Average DRF-DR{F}_{Highest frequency})\end{array}$ (6)

The threshold as well as the upper and the lower bound once determined remains constant for that specific setup.

In order to explain how to use the proposed algorithm shown in Figure 10, DRF responses of the waves propagating between Act 1 to Sen 2 gathered experimentally are plotted in Figure 11, where markers are removed for clarity.

Figure 11 Multi-frequency DRF analysis for Act 1 - Sen 2.

Referring to Figure 11, the first step is to calculate the individual DRF for each excitation frequency, in this case for 100 kHz and 200 kHz. Then, an average of all the DRFs is taken, shown as a solid black line. For selecting the threshold, the average DRF value at 35000 cycles, where a 0.5 mm crack was confirmed, is chosen. The threshold was found to be 0.86 for Act 1 - Sen 2. The upper and lower bounds are also chosen at 35000 cycles as a difference between the average DRF and the lowest and the highest frequency DRF respectively using Eqn. 6. The idea is to have the upper and lower bounds both within the lowest and highest frequency DRF spread (calculated using Eqn. 5). Therefore, at 35000 cycles, the upper and lower bound was found to be (average DRF±0.025), such that the lowest frequency DRF ≥ upper bound and the highest frequency DRF ≤ lower bounds.

Figure 12 Multi-frequency DRF analysis for, (a) Act 1 – Sen 4 and (b) Act 3 – Sen 4.

In other words, the DRF methodology for detecting damage consists of computing the average DRF of all the excited frequencies (black line in Figure 13), determining the threshold value for a confirmed crack and computing the upper and lower bounds at that particular confirmed crack length. Therefore, using this technique, damage is said to be present if the average DRF is less than or equal to the threshold value of 0.86 and the upper and lower bounds (average DRF±0.025) are within the lowest and highest frequency spread, as well as the lower frequency (100 kHz) DRF is greater than the higher frequency (200 kHz) DRF for this experimental setup.

Figure 13 Multi-frequency “cycle-free baseline” DRF analysis at 0 cycle.

Experimental results for the other wave paths are shown in Figure 12.

From Figure 12, it can be observed that none of the average DRFs for waves propagating between Act 1 - Sen 4 and Act 3 - Sen 4 were below the threshold value of 0.86; thus, showing no indications of damage within their paths.

It is well known that increasing the load will enhance crack detection by opening up the crack surfaces. Therefore, instead of using the fatigue cycling data, the load data is used at any given fatigue cycle, i.e. the baseline is taken at the lowest tensile load as a “cycle-free baseline” technique. The idea behind the “cycle-free baseline” technique is to interrogate the structure during the same cycle but at different loading conditions. The advantage of using this technique is to minimize the false calls due to sensor degradation caused by fatigue and environmental cycling.¹⁶ For clarity and brevity purposes, only the wave path of Act 1 – Sen 2, Act 1 – Sen 4, and Act 3 – Sen 4 are shown for 0, 35000, and 55000 cycles to demonstrate this “cycle-free baseline” technique in Figure 13-15 respectively. The same threshold values of 0.86 and an upper and lower bounds of average DRF±0.025 are used for the “cycle-free baseline” analysis.

Figure 14 Multi-frequency “cycle-free baseline” DRF analysis at 35000 cycles.

Figure 15 Multi-frequency “cycle-free baseline” DRF analysis at 55000 cycles.

Using the “cycle-free baseline” technique, no signs of damage was present at 0 cycle, as shown in Figure 13, where all the average DRFs were well above the threshold value. The indication of damage can be found at 35000 cycles at approximately 1800 N load, as shown in Figure 14a for the wave path between Act 1 to Sen 2, which is directly in line with the crack. Also the spread at the nearest data point at 500 lbf [2224.1 N] was 0.14 (Figure 14a) as compared to 0.05 at 35000 cycles but at no load [0 N] condition (Figure 11). It can be noted that signs of damage were found for Act 1 to Sen 2 at 55000 cycles at a load of approximately 1200 N load, as shown in Figure 15a, which means that as the damage grows, the application of even a small load is capable of facilitating damage detection. This is expected as the application of load will open up the crack surfaces, interfering with the propagating waves; thereby enhancing detectability. No indications of damage were found for all other wave paths at 35000 and 55000 cycles, as shown in Figure 14b,c and Figure 15b,c respectively.

The “cycle-free baseline” technique may be beneficial in reducing the false calls associated with sensor degradation as the structure is interrogated using the same sensor state for determining the baseline and the change. This technique also eliminates the requirement to store and process all the data associated with each cycle. However, the downside to this technique is the requirement for applying discrete loads to the structure. For aircraft applications this can be done before and after fueling or before and after loading the aircraft with cargo and/or passengers. Unfortunately, this approach may not be able to detect the damage if it is located on the compressive side of the structure, an issue which will be addressed in the future. It was also interesting to note that above the threshold tensile load of approximately 1000 lbf [4448 N] for the investigated case, the application of higher loads provided no significant changes to the calculated DRF, as shown in Figure 14a to Figure 15a. Similar phenomenon was also observed by Pavelko in.⁸

In order to verify the proposed DRF algorithm, a Finite Element Model (FEM) was developed mimicking the experimental setup including all the boundary conditions, which is discussed in the following section.

A Finite Element Model (FEM) of the C-Channel was developed in ABAQUS CAE™ version 6.16. The primary objective of this model was to verify the proposed method described previously in this manuscript. The authors used this model in order to understand the effects of residual stress fields around a fatigue crack on Lamb wave propagation behaviour, as described in.¹⁸ The model consisted of three distinct components: (i) the aluminium C-Channel section; (ii) four piezoelectric actuator / sensor discs connected to the C-Channel with a tie constraint; and (iii) two rigid swivel connectors tied onto the C-Channel with a prescribed boundary conditions that allowed for the C-Channel to rotate during the load application, as shown in Figure 16.

Figure 16 Finite element model of the C-Channel.

The 7075-T651 C-Channel was considered to have a Young’s modulus of 72.9 GPa, a density of 2800 kg/m³ and a Poisson’s Ratio of 0.33.¹⁹ 

The PZT actuator and sensors used in this study were single sensors from Acellent Inc., which were simulated as cylindrical disks of 6.5 mm in diameter with a thickness of 0.25 mm. The piezoelectric actuator/sensors were assigned orthotropic Piezoelectric Navy I material with the following properties: E₁₁ = E₂₂ = 80 GPa; E₃₃ = 68 GPa; G₁₃ = G₂₃ = 30.5 GPa; G₁₂ = 29.0 GPa; and Poisson’s Ratio v₁₂ = v₃₁ = v₃₂ = 0.31. The piezoelectric charge constants were set to: d₃₁ = -125×10^-12 C/N; d₃₃ = 290×10^-12 C/N; while d₁₅ = 480×10^-12 C/N. Finally, the relative dielectric constants were assigned values of k₁₁ = k₂₂ = 1275, and k₃₃ = 1320 (ε_o = 8.854×10^-12 F/m), while the density was set to 7600 kg/m³.²⁰

The model consisted of a total of 847,247 elements. The solution data file was saved at a time step of 1×10^-7 seconds and a mesh element size of less than 1 mm was used. In order to mimic the experimental results and reduce the number of assumptions, the actuation signal captured by the digital oscilloscope was used as the input signal in the FEM.

A Windows 7 computer with two Intel Xeon CPU 2650V3 (a total of 20 physical CPUs) running at 2.30 GHz with 128 Gigabytes of RAM was used in this study. Despite the high computational resource, many of the simulations took over a week to converge for a total time window of 350 microseconds. Therefore, to minimize the overall simulation run time, only three major paths were analysed and simulated. The first path consisted of waves propagating between Actuator 1 (Act 1) to Sensor 2 (Sen 2), which was in line with the damage site. The second path was between Act 1 to Sen 4, which was diagonal to the damage site and the third path was between Act 3 to Sen 4, which was outside of the damage site. The acquired FEM signals were filtered using a zero-phase shift (filtfilt) Butterworth band-pass filter with a pass band between 1 kHz and the excitation frequency + 200 kHz in Matlab™.

A simplified model of the crack was generated by extending the saw-cut in the FEM with a width of 0.25 mm and an initial length of 0.4 mm. The saw-cut was increased in length to 2.5 mm in steps of (0.5 mm, 1 mm, 1.5 mm, and 2.1 mm) to mimic a total of 2.1 mm growth from the initial saw-cut, as shown in Figure 17.

Figure 17 Simplified crack model in FEM.

The FEM result for the wave propagating from Act 1 to Sen 2, which is in line with the growing crack is shown alongside the experimental result plotted with respect to crack lengths in Figure 18. The same threshold (0.86) as well as upper and lower bounds (average DRF±0.025) that were determined experimentally were used for detecting damage using the FEM data.

Figure 18 Results of DRF analysis for Act 1 – Sen 2: (a) FEM, (b) Experimental.

As shown in Figure 18a, for the wave propagating between Act 1 - Sen 2, which was in direct path of the growing crack, the FEM followed the same trends as were found by the experimental results provided in Figure 18b, i.e., in both the experimental and the FEM results, the DRF of the waves excited at 100 kHz and 200 kHz were close together up to a certain crack length and only started to diverge when the crack length was long enough to affect their propagation characteristics. Waves excited at 200 kHz were more sensitive to the presence of damage as compared to the waves excited at 100 kHz. Using the DRF algorithm, damage can be said to be present in the FEM data, at a crack length of 2.1 mm as compared to 0.5 mm determined by the experimental results. However, the DRF spread was demonstrated in the FEM for a crack length between 1 mm to 1.5 mm.

The FEM results for the waves travelling between Act 1 - Sen 4 and Act 3 – Sen 4 are shown in Figure 19a and Figure 20a respectively.

Figure 19 Results of DRF analysis for Act 1 – Sen 4: (a) FEM, (b) Experimental.

Figure 20 Results of DRF analysis for Act 3 – Sen 4, (a) FEM, (b) Experimental.

As seen in Figure 19a and Figure 20a, the average DRF values were above the threshold value set by the experimental results; thus, showing no signs of damage in their direct paths.

It is to be noted that the FEM model used in this work is the simplest representation of a crack and does not account for residual stresses formed during the crack propagation in addition to wave attenuation at different frequency. The authors’ previous work provided in reference¹⁸ demonstrated that the residual stress has an effect on the propagation characteristics of guided waves. Despite the simplistic crack model, the FEM results display that the waves excited at a higher frequency corresponding to a smaller wavelength are in fact more reactive to the presence of the damage in their path, as compared to the waves generated at a lower frequency corresponding to a longer wavelength.

In order for the DRF to be effectively used, the threshold value should have been previously determined from multiple experimental results. This is equivalent to the current practice by the Non Destructive Evaluation (NDE) community, which requires inspectors to calibrate their NDE system with respect to using the same instrument and a calibration block of the same material being inspected. The DRF becomes more useful as the number of experimental data sets increases. The first couple of experimental data sets can be used to select an appropriate threshold, in addition to the upper and lower bounds. However, once these critical parameters are selected based upon previous experimental results, these parameters can be used for identifying damage at a critical size in a unknown coupon of the same geometry, configuration, and material type.

A method to detect damage along an actuator and sensor path was presented based on the Damage Response Factor (DRF) approach, which combines the changes in the Cross Correlation (CC), Energy Ratio (ER) and Amplitude Ratio (AR) between the current signal and the baseline signal. It was found that a drop in these parameters calculated separately or even through a combination of a DRF below a threshold value alone is not sufficient to detect the presence of damage. Therefore, in addition to the commonly used threshold value, the algorithm presented here uses the upper and lower bounds on the average DRF value along with the separation of the DRF based on excitation frequency. The algorithm is based on observing the trends of guided waves excited at multiple frequencies to witness how the waves with smaller wavelengths (corresponding to a higher frequency excitation) behave as compared to the waves with longer wavelengths (associated with a lower frequency excitation). By combining these criteria, a method for damage detection along an actuator and sensor path has been developed and proven experimentally and numerically through FEM. Also, based on the effect that applied load had on the propagation characteristics of Lamb waves, a “cycle-free baseline” technique was proposed; whereby, the minimal applied tensile load within each cycle was used as a baseline as opposed to the baseline taken at zero cycle. The “cycle-free baseline” technique demonstrated that as the damage grows, the application of even a small load facilitated damage detection. Finally, it was observed that there existed a threshold tensile load for crack detection; the application of higher loads did not significantly increase the effectiveness of the proposed DRF algorithm.

The authors would like to thank Defence Research and Development Canada (DRDC) for providing the funding as well as Michel Delannoy, Richard Desnoyers, Andy Christie, Stephane Cloutier, Roy Campbell, John MacMillan, and Dmitrii Klishch for their technical support. In addition, the Holistic Structural Integrity Process Laboratory at Clarkson University would like to acknowledge the support of NVIDIA Corporation for their donation of a TESLA K40 and Quadro P6000 GPU hardware card, used for developing and solving the FEM.

Authors declare that there is no conflict of interest.

1. MIL-STD-1530D, Department of Defense Standard Practice – Aircraft Structural Integrity Program (ASIP); 2016.
2. Pant S, Martinez M, Yanishevsky M, et al. Damage detection methodology for Structural Health Monitoring (SHM) applications on multi-frequency anti-symmetric guided waves. 9th European Workshop on Structural Health Monitoring: Manchester, UK; 2018.
3. Ihn JB, Chang FK. Detection and monitoring of hidden fatigue crack growth using a built-in piezoelectric sensor/actuator network: I. Diagnostics. Smart Mater Struct. 2004;13:609–620.
4. Giurgiutiu V, Xu B, Chao Y, et al. Smart sensors for monitoring crack growth under fatigue loading conditions. Smart Struct Syst. 2006;2(2):101–113.
5. Ryles M, Ngau FH, McDonald I, et al. Comparative study of nonlinear acoustic and Lamb wave techniques for fatigue crack detection in metallic structures. Fatigue Fract Eng Mater Struct. 2008;31(8):674–683.
6. Lu Y, Ye L, Su Z, et al. Quantitative assessment of through-thickness crack size based on Lamb wave scattering in aluminum plates. NDT&E Int. 2008;41(1):59–68.
7. Pavelko V, Pavelko I, Ozolinsh E. The effect of Lamb wave interaction with fatigue crack in thin Al sheet. Key Eng Mater. 2012;488:65–68.
8. Pavelko V. Application of the fatigue crack opening/closing effect for aircraft SHM. 7th International Symposium on NDT in Aerospace: Bremen, Germany; 2015.
9. Lee SJ, Michaels JE, Michaels T. Comparison of the effects of applied loads and temperature variations on guided wave propagation. Review of Progress in Quantitative Nondestructive Evaluation: Burlington, USA; 2011.175–182 p.
10. Gandhi N, Michaels JE, Lee SJ. Acoustoelastic Lamb wave propagation in biaxially stressed plates. J Acoust Soc Am. 2012;132(3):1284–1293.
11. Boon MJGN, Zarouchas D, Martinez M, et al. Temperature and load effects on acoustic emission signals for structural health monitoring applications. 7th European Workshop on Structural Health Monitoring: Nantes, France; 2014.
12. Chen X, Michaels JE, Lee SJ, et al. Load-differential imaging for detection and localization of fatigue cracks using Lamb waves. NDT&E Int. 2012;51:142–149.
13. Chen X, Michaels JE, Michaels TE. Load-enhanced Lamb wave techniques for characterization of scatters in structures with complex geometries. Mater Eval. 2014;72:1314–1324.
14. Corrcoef, Correlation coefficients, MathWorks Documentation.
15. ImageJ, Image Processing and Analysis in Java.
16. Martinez M, Li G, Backman D, et al. Crack detection on composite and metallic aerospace structures. 4th European Workshop on Structural Health Monitoring; 2008. 560–569 p.
17. Pant S, Backman D, Benak T, et al. Reliability assessment of different SHM and load monitoring systems under load and environmental conditions. 28th International Committee on Aeronautical Fatigue and Structural Integrity: Helsinki, Finland; 2015.
18. Martinez M, Pant S, Yanishevsky M, et al. Residual stress effects of a fatigue crack on guided Lamb waves. Smart Mater Struct. 2017;26(11):1–5.
19. MIL-HDBK-5H, Military Handbook, Metallic Materials and Elements for Aerospace Vehicle Structures; 1998.
20. APC Materials. Physical and piezoelectric properties of APC materials; 2018.