eISSN: 2576-4500


Research Article Volume 1 Issue 1
Department of Mechanical Engineering, Ecole Polytechnique de Montreal, Canada
Correspondence: Jean Yves Trepanier, Department of Mechanical Engineering, Ecole Polytechnique de Montreal, Montreal, Quebec, Canada
Received: May 10, 2017 | Published: June 20, 2017
Citation: Trepanier JY, Lupien A, Tribes C, et al. A 3d parameterization for transonic fan blade multidisciplinary design. Aeron Aero Open Access J. 2017;1(1):31-39 DOI: 10.15406/aaoaj.2017.01.00004
This paper presents a new tridimensional approach for transonic fan blade design. The proposed parameterization uses parameters closely linked to aerodynamic performance of blades, such as beta angles and thickness distributions and allows the control of these parameters in both axial and spans wise directions independently. In addition, a multi-level modification approach is presented, which allows modifying the blade geometry locally or globally. This multi-level approach enables to use a reduced number of parameters for preliminary design optimizations and to switch, in a seamless way, to higher precision for final design optimizations. The parameterization is validated by the replication and modification of the NASA Rotor 67 and examples are given of the application of the parameterization to multidisciplinary fan blade design.
Keywords: parameterization, fan blade, multi-level, aerodynamic design, euler equation, poissons ratio, youngs modulus, bezier curve, blade curvature, transonic fan
The design of modern turbofans blades involves a complex set of requirements from various disciplines with often opposing needs in terms of blade characteristics. The main disciplines involved are the blade aerodynamics, responsible for the energy transfer and the isentropic efficiency of the blade rows, structural analysis, responsible for blade integrity and dynamic analysis, responsible for controlling the vibration modes. The design process often involves many specialists from different departments and numerous computational tools of various natures, from simple mathematical relations to complex physics based computational models, such as Computational Fluid Dynamics and Computational Structural Dynamics. In the traditional approach, the aerodynamics designers propose a first blade design, which is then modified by the structure and dynamics groups to meet their requirements and send back to the aerodynamicists for verification. Many iteration between these groups are often required and the process is usually stopped when a feasible design is reached.
However, today's competitive market requires more from the design process. The process itself must be efficient and streamlined to facilitate iterations and enable automation. Furthermore, the process should support design optimization to increase product performance and reduce product cost, increasing value for the customers. Such a goal requires a rethinking of the traditional design approach and as discussed by various authors Vandenbrande et al.,1 Dawes et al.,2 Crawford and Haimes,3 Pierret et al.,4 Delap et al.,5 Idahosa et al.,6 Samareh7 asks for a more integrated design system. These systems put the geometric parametric model at their center in order to support all disciplines simultaneously.
In the context of developing an integrated multidisciplinary design system for turbofan blades, the present paper put the emphasis on their parametric geometric definition. Based on the work of Samareh.7 We set forth in the next section the characteristics required from the parameterization for driving various multidisciplinary analysis in an integrated design system. In Section 3, we propose an original approach to meet the requirements and we detail the proposed parameterization. As a validation, a measure of its accuracy in representing a typical fan blade is performed. Section 4 will describe how the parameterization has been placed at the center of an integrated design system and examples of disciplinary analysis and design optimizations will be given. The conclusion will summarizes the achievements and will state the next steps towards achieving a complete integrated multidisciplinary design system for turbofan blades.
Working on the multidisciplinary high fidelity design of future aircraft concepts, Samareh7 proposed a set of ten criteria for the application of multidisciplinary design optimization (MDO) to complex 3D models. Among these criteria, six have been judged more important for the present application. These criteria and their rationale are given below
To our knowledge, no existing approach from literature allows to respect simultaneously all the six criteria.
The first five criteria are directly related to the design of the parameterization and will be discussed in the next section. Our approach to respect these criteria was to perform a literature review of available parameterization and to link these to the requirements. Then, we have selected various components from literature and we have combined them to propose a new parameterization which can respect all criteria. Note that the most difficult criteria is the second one, since it implies an engineering judgment. The sixth criteria about CAD connection is an important issue which has been discussed by various authors.3,5,8 Details about our strategy to respect these criteria will be given in Section 4. Once the parameterization is selected and implemented, a two step validation procedure has been applied. In section 3.4, we first show the accuracy of the parameterization. In section 4, we illustrate the flexibility of this new approach on both aerodynamic and multidisciplinary design problems.
As dictated by requirement 2, a proper blade parameterization should link seamlessly with the requirements of analysis methods and the experience of the designers, from conceptual to detailed design. From a structural and vibration point of view, blade thickness span wise distribution remains the most influential parameter and following various authors,4,6,9 we also select the blade thickness as a primary variable. Because thickness also influences the aerodynamics of the blade, it clearly carries a strong multidisciplinary coupling, making it a good choice for shared variable. From an aerothermodynamics point of view, the most important relation in turbomachinery is the Euler equation, which relates energy transfer to the change in tangential velocity of the flow, as represented by velocity triangles. The changes in tangential velocity being controlled by the blade angles, these latter represent a natural design variable for a designer. Various authors have proposed various ways to de ne the blade shape. Idahosa et al.6 parameterized the blade angle using Bezier curve. Pierret et al.4 proposed using mean camber line distribution as a design variable. However, as discussed by various authors,10-12 flow properties also depend strongly on blade curvature; thus a direct control on the variation of the blade angles along the blade chord is also important to control diffusion. We thus propose to use both the angle and the rate of variation of the angle as design variables. In addition, a further refinement of the parameterization proposed concerns the radial distribution of these properties. As discussed by Korakianitis et al.10 Miller et al.13 through- flow analysis is performed during preliminary design to provide streamlines in the meridional plane and the blade angles are extracted from those analyses on the stream surfaces. This complicates the blade creation but is important to bring the initial design much closer to optimal performance. The proposed parameterization thus separates the specification and control of the blade angle and thickness distributions from the blade construction on stream surfaces. These two steps will be described in the following subsections, and later linked to provide a full 3D parametric description of the fan blades.
Section parameterization
The proposed blade section parameterization involves the specification and control of blade angle, angle rate of variation, thickness and thickness rate of variation along the blade chord. In practice, since the angle distribution is more important on the suction side than on the pressure side to control diffusion, the -angle values and derivatives are used to generate the suction side of the blade and the thickness distribution is added as an o set of the suction side to generate the pressure side. This method presents some similarities to the work of Idahosa et al.6 and Miller et al.,13 except that the angles do not define the camber line but directly the suction surface. The four distributions are defined with a set of points, typically three to five along the blade chord, as illustrated on Figure 1. On Figure 1, the black dots represent the points specified by the designer and these points control the distributions. For the angle and angle rate of variation, the values are given as a function of the percentage of meridional chord (pcm) in order to allow an easy rescaling of the blade for different blade length. The definition of the meridional chord is given on Figure 2.
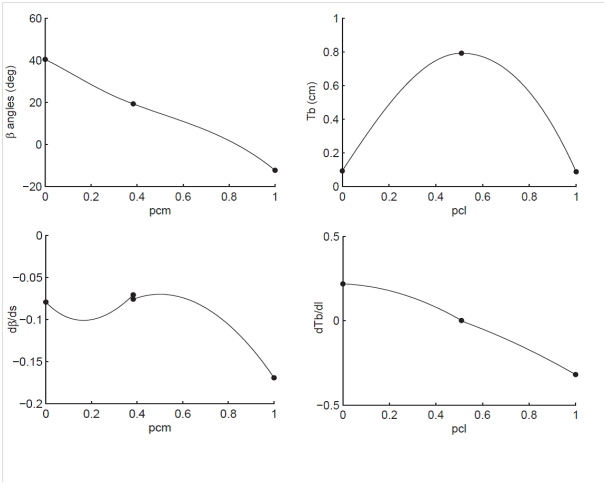
Figure 1 Left: Beta angle and derivative distributions; Right: Thickness and derivative distribution.
It is measured along the streamlines at each radial position, from the leading edge to the trailing edge of the blade. These leading edge and trailing edge position on the meridional plane are an input to the blade generation algorithm. Figure 1 also illustrates one more characteristics of the parameterizations the values, angle and thickness, are continuous distributions while the derivatives support discontinuities at the inner points, as illustrated for the angle derivative distribution. In practice, continuous derivative can be also imposed but discontinuities in slope are allowed for more generality.
The distribution of angle is then constructed from the set of points using piecewise cubic polynomial between points. The curve between two points i and i+1 is then given by Equation 1, where s is the arc length of the resulting suction side curve.
(1)
The coefficients are obtained by solving the following system of equations:
(2)
Since the distribution is computed with respect to the curve arc length (s) unknown beforehand, it is required to iterate this variable until the corresponding percentage of meridional chord (pcm) is obtained. The link between those two coordinates is given by Equation 3, where mc represents the meridional chord.
(3)
The Mat lab optimization algorithm f minsearch is used to match the correct blade length (s).
The thickness distribution is computed in a similar way with the exception that it is defined as a function of the pcl, the percentage of the suction side curve arc length. As a result, there is no need to iterate since there is no coordinate transformation between the curve definition and the computed distribution. The thickness distribution is computed using Equation 4, where l is the suction side curve arc length. The link between l and pcl (percentage of suction side curve arc length) is straightforward.
(4)
The coefficients are calculated by solving the matrix system given by Equation 5.
(5)
The section is closed at the leading and trailing edges with circular arcs.
Section creation
In order to fully exploit the information obtained from streamline curvature through- flow analysis codes, the fan blade is generated on a stream surface using a methodology similar to Miller et al.13 As explained in the previous section, the β-angle distribution of each section is used to create the suction side of the blade and the pressure side is created as an o set to the suction side using the thickness distribution. Since each section lies on a streamline revolution surface (Figure 2 & 3), two coordinate transformations are required: the (m, rθ) space, in which the thickness of the blade is defined, is length preserving, while the (m,θ) space, used to define the angle distribution, is angle preserving. Those two spaces are derived from the streamline revolution surfaces coordinates (r, z,θ), illustrated on Figure 3. The reader can refer to Miller et al.13 for the characteristics of these transformations.
The m coordinate represents the meridional direction of the streamline revolution surface and is defined by Equation 6, where the index u represents the derivative with respect to u.
(6)
The m’ coordinate is defined as:
(7)
The β-angle distribution (Figure 1) is converted into a slope distribution and integration is performed to build the suction side in the (m’,θ ) space, as illustrated in Figure 5, where θ is given as:
(8)
The thickness distribution is then added perpendicularly to the mean camber line in the length preserving space (m, rθ ) to create the pressure side of the section, as illustrated in Figure 6.
3D Blade Surface Definition
The previous sections have detailed the construction of the airfoil sections on revolution stream surfaces. In order to build the full 3D blade, a strategy to interpolate these blades in the span wise direction is needed. According to Requirement 3, the 3D approach proposed has the objective of keeping a low number of parameters to generate fan blades. One of the reasons why the number of parameters can grow rapidly for complex fan blades is that sections have usually independent sets of parameters.14 So the goal was to eliminate the section by section parameterization and replace it with a more 3D oriented approach.
In order to reduce the number of parameters, Abdelhamid 15 has proposed a parameterization of blades with 3D Bezier surfaces. However, such parameterization does not respect Requirement 2 because it lacks the relation between the geometric parameters and the flow characteristics. The same is found in the Free Form Deformation approach proposed in John et al.16 The consequence is that such parameterization can hardly be used by a design engineer because the relation between turbomachinery theory and design parameters, such as Bezier control points, is not straight forward. So the proposed parameterization keeps the engineers parameters from the section by section parameterization and adds a second dimension in the span-wise direction. A 3D surface is then obtained representing parameters in both axial and span wise directions, as illustrated in Figure 7 for both angle and thickness distributions.
This 3D approach for the proposed parameterization brings also the possibility to control the distribution of the parameters over the whole blade geometry instead of changing each section independently. This ability will help to ensure smooth and controlled variations of the blade geometry required to obtain smooth flow properties along the span.
In the present section, we will illustrate how accurately the proposed parameterization can match a typical fan blade. This validation serves two purposes: first, it helps demonstrate that the proposed parameterization is flexible and powerful enough to represent a real blade accurately; second, the process of fitting a given blade with the proposed parameterization is often a required step before a design modification and optimization of that blade can be performed. The fan selected for this validation is the NASA Rotor 67, a widely studied 22 blades rotor with a low-aspect ratio transonic axial-flow fan. Its geometry, taken as reference, is given in the work of Strazisar et al.14
In order to replicate the NASA Rotor 67 geometry with the proposed parameterization, it was necessary to extract the required parameters from the geometry coordinates given in Strazisar et al.14 Beta (β) angles and thickness distributions are required for each of the 14 sections of the geometry. In an attempt to keep a low number of design variables, every section was matched by optimization with only 3 control points and their derivatives. For the curvature distribution, both starting and ending points of the distributions are used as first and last control points, leaving 5 variables for the optimization, which are: value at the middle point, values of curvature at the first and last control point and a discontinuous curvature (2 values) for the middle point. Concerning the thickness distribution, the middle point slope is fixed at zero and the 3 optimization variables are the middle point position and the derivative at the first and last control points. These 8 design variables were then used in a geometric optimization formulation, where the objective function to minimize is the area between the reference blade and the blade computed using the parameterization. This process is repeated for every section. Figure 8 illustrates the results of the fitting for sections 5 and 10 of the Rotor 67 fan. On Figure 8, the small "x" corresponds to the values extracted from the reference geometry, while the dots and the full line correspond to the approximation obtained with the present parameterization. One can observe that the parameterization allows for a very accurate representation of Rotor 67 angle and thickness distributions.
Concerning the span wise distribution of parameters, Figure 9 illustrates the variation of β-angles at the leading edge of the Rotor 67 blade for the 14 sections provided (left side-a). This distribution has been matched using seven control points in the span wise direction, as shown in Figure 10 (right side-b).
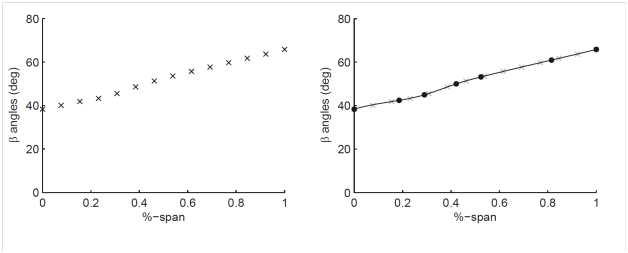
Figure 9 Beta angles at leading edge (a) Left: original points from 14 sections (b) Right: Spline representation of the spanwise distribution.
The final result of matching the Rotor 67 blade with the proposed parameterization is illustrated on Figure 10 where the reference Rotor 67 is shown in dark and the matched blade in light. An analysis of the blades shows that the blade obtained with the present parameterization represents accurately the reference rotor with a maximum deviation of 0.36 mm, which represents 0.4% with respect to the chord.
In order to better evaluate the accuracy of the matched blade compared to the reference one, a comparison of the aerodynamic performance based on high fidelity CFD analysis is done. Because of the non-linearity of the transonic regime, small variations of the blade geometry can induce important change in flow characteristics. The two blades are thus compared side-by-side on a transonic CFD case to assess the importance of the geometric differences. Both cases are performed on the same mesh and at the same mass flow and Reynolds number. Figure 11 illustrates the comparison with the experimental data of the Mach contour at peak efficiency for both reference and fitted blade. Experimental data is taken from the work of Strazisar et al. 14 As observed, the difference of the calculated results between the reference and the fitted blade is very minimal. As a global comparison, the efficiency and total pressure ratio of both blades are given in Table 1. Excellent agreement is obtained on these metrics.
|
Reference blade |
Matched blade |
Difference % |
Efficiency |
0.923 |
0.924 |
0.1 |
Total Pressure Ratio |
1.643 |
1.646 |
0.18 |
Table 1 Efficiency and total pressure ratio comparison
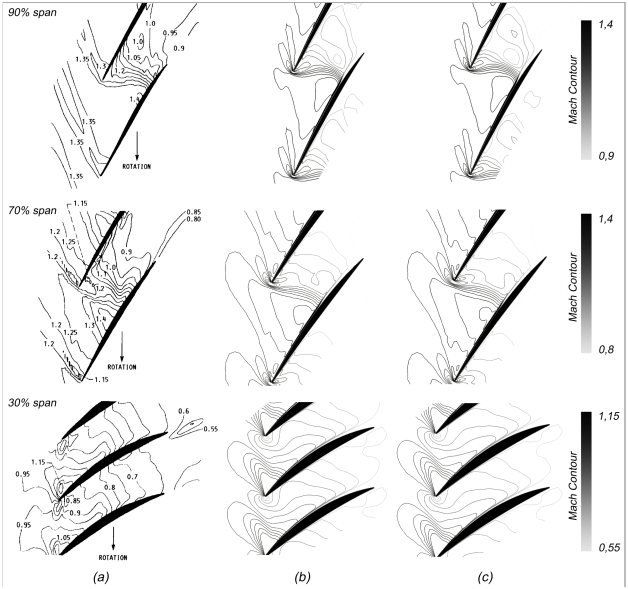
Figure 11 Mach contour comparison (near peak efficiency) (a) Experimental Data (b) Reference blade (c) Matched blade.
Global blade modification
In the context of design optimization, the requirement on the parameterization varies from preliminary to conceptual design. Initially, one usually wants to use a low number of design variables and explore the design space more thoroughly. As the design shapes, one can use the full flexibility of the parameterization to focus on local design optimizations. In order to reduce the number of design variables required for a blade modification, a multi-level control approach has thus been developed. This method sits on top of the presented parameterization. The approach allows the user to determine a specific requirement for any span wise parameter value and extend smoothly this modification to neighboring sections. For example, consider a case where an aerodynamics designer wants to increase the trailing edge blade angle by 5 degrees at 70% span as illustrated in Figure 12(a). The control points needs to be moved to match this requirement. Because there are an infinite number of curves that match that specific requirement, an influence function is proposed in order to set a relation between the control points of the various neighboring sections. This influence function is based on a Gaussian curve where the variance can be modified to vary the distance of influence. This concept is illustrated in Figure 12(b) and Figure 12(c), where the influence level is more local in Figure 12(b) and more global in Figure 12(c). This multi-level capability allows the design system to meet Requirements 3 to 5. Examples of design using this approach will be given in the following sections.
The present blade parameterization is intended to serve as a basis for a multidisciplinary design system for fan blade design. Many authors have emphasizes the importance of putting the geometry at the center of such systems.2,3 In the present case, the parameterization described in the previous sections is using parameters and transformations which make it difficult to be implemented directly into a CAD system. In order to fully control the parameterization, a MATLAB implementation has been preferred. In addition, a strong and direct link to a CAD system is also proposed to offer a virtually CAD-Centric design system, in respect of Requirement 6. The system is illustrated on Figure 13 together with the various elements integrated to provide the analysis and optimization capabilities.
Referring to Figure 13, the blade geometry module comprises both the MATLAB parameterization and a CATIA solid model. Blades created using MATLAB are transferred as a fine discretization to CATIA where a solid model is constructed. The aerodynamics module comprises two sub-modules: the TurboGrid mesh generation tool and the CFX flow solver, which accurately compute the aerodynamic performance of a given blade. The structure and dynamics module starts with an APDL script which generates a mesh of the blade and disk assembly for mechanical analyses. Then, stress analysis is performed in ANSYS and a pre-stressed model is used to compute natural frequencies of the rotating blade. Integration is obtained using the iSIGHT framework, which provides in addition capabilities for parametric studies, DOE, approximation models and various optimization methods. iSIGHT controls directly the blade shape using the Beta-thickness distributions specified in an Excel le and the full system is completely integrated and automated.
Examples
Aerodynamic redesign of Rotor 67: As a first example, we consider the aerodynamic redesign of the well known Rotor 67 from NASA.14 The rotor has 22 blades and 16043 RPM design speed. The rotor design point pressure ratio is 1.63 and a mass flow rate of 33.25 kg/s. For the present exercise, a medium size mesh (150,000 nodes) is used together with the SST (Shear Stress Transport) turbulence model. With these parameters, a converged solution is obtained in 18 min with residual 1E-05 on 4 Intel Core i7 (16 GB RAM) processors. The initial geometry is the Rotor 67 and the initial values for the design variables are those found in the validation section above. The optimization problem is to maximize the aerodynamic efficiency of the fan, while maintaining the pressure ratio and the outlet corrected mass flow rate constant. The mass flow rate constant is imposed directly by the CFX flow solver while the pressure ration constraint is managed by the optimizer. This is mathematically expressed as:
(9)
The aerodynamic optimization is performed by taking 17-geometrical de-sign variables including beta angles, beta curvature, stacking, and maximum thickness position along chord. For this aerodynamic optimization, the blade thickness is not taken as a parameter, since the blade thickness is controlled by the multidisciplinary coupling with structures and vibrations, as discussed later. For now, only the maximum blade thickness chord wise position is allowed to vary.
Many optimization techniques have been applied, including Genetic Algorithms (GA), Adaptive Simulated Annealing (ASA) and Pointer from the iSIGHT framework and NOMAD, a freely available optimization package.
For the present work, the goal was to show the robustness of the integration scheme. Figure 14 shows the convergence of the optimization process. Most methods reach a plateau in approximately 500 evaluations of the function. However, even if the maximum efficiency reached by the various methods are very close to each other, different blade shapes have been found, as illustrated in Figure 15. In particular, the NOMAD algorithm found a backward stacking as compared to the other methods. Figure 16 shows the Mach contours at 30% span resulting from the various optimization runs. All methods have reduced the strength of the leading edge shock and they also all reduced the size of the separated flow region at trailing edge.
The fact that different solutions can be found by different optimization approaches is not too surprising since the fan design problem at hand is highly non-linear and multi-modal. However, these options can be reviewed by an experience designer who will select the best solution to finalize his work. These results demonstrate the robustness of the proposed parameterization and integration scheme in the construction of an automated design system. Application to a multidisciplinary design problem is given below.
Multidisciplinary redesign of Rotor 67: As a second example, a multidisciplinary design optimization is performed to improve the aerodynamics of the Rotor 67 transonic fan at design point while respecting constraints from other disciplines. The main objective is again to maximize the aerodynamic efficiency under pressure ratio and mass flow rate constraints. However, additional constraints are added from other disciplines: the maximum stress in the blade is constrained to be less or equal to the maximum stress of the original Rotor 67; and vibration frequency ranges are forbidden to avoid resonances. Following Doi & Alonso,16 Youngs modulus is taken as Ey = 1.422e+11 Pa, Poissons ratio, = 0.3, and density = 4539.5 kg/m3. For the vibration constraints, one rotational speed, E, is defined as E=267.4 Hz based on RPM at design point. The blade vibration frequencies should not lie close to the engine running speeds i.e.1E, 2E, 4E, 8E and NE, etc. For the present example, the vibration frequencies are forbidden within a range of +/5% of the running speeds 1E, 2E and 4E.
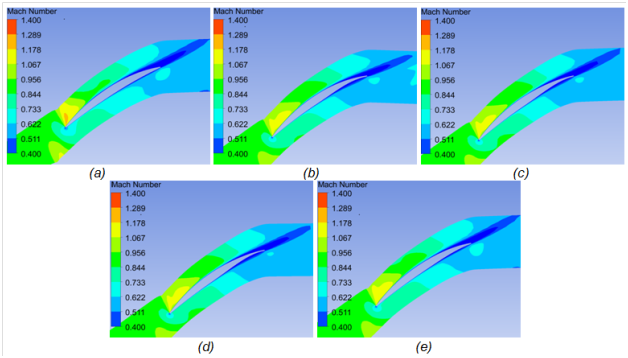
Figure 16 Mach contours at 30% span. (a) Original Rotor 67, (b) NOMAD, (c) ASA, (d) Pointer, (e) GA.
This multidisciplinary optimization is performed using 19 design variables, from which 18 are those used in the aerodynamic optimization problem above, plus the maximum thickness along the span wise direction. ASA is chosen as the optimization technique.
Stress and dynamic analyses are performed in ANSYS mechanical APDL. The same mesh is used for both analysis, using the solid element 10 node187 and a mesh size of 150,000 nodes. The stress computation takes 1 min for a single analysis. For dynamic analysis, the ANSYS model Block Lanczos method has been chosen. Centrifugal staining is included but the aerodynamic pressure loading is not considered since deformation and stress are largely caused by the centrifugal force.
The first, second and third mode shouldn't lie in between 260-274, 521-548, 1042-1096, 1564-1644, and 2085-2192 Hz. The first three natural frequencies of Rotor 67 are associated to the torsional motion near the tip. As 1st and 3rd frequency mode are trying to be push up which required reduction in mass/thickness at the same time 2nd and is trying to push down which requires the increment in mass/thickness. This contradiction makes the optimizer job harder. An optimized design is obtained with the improvement in efficiency +1% while satisfying the dynamic constraints, maximum stress lower than the maximum stress of Rotor 67, mass flow rate and pressure ratio within 0.5% of Rotor 67. Results are presented in Table 2.
|
Optimization results |
FIO-optimized |
Rotor 67 |
Aero |
Mass flow rate (Kg/sec) |
1.520 (+0.2%) |
1.517 |
Pressure Ratio |
1.616 (+0.18%) |
1.613 |
|
Efficiency |
0.9071 (+1.06%) |
0.8976 |
|
Dynamic Frequency mode (Hz) |
First, F1 |
551 |
521 |
Second, F2 |
1286 |
951 |
|
Third, F3 |
1723 |
1966 |
|
Structure |
Maximum Stress (Mpa) |
467 |
521 |
Table 2 Comparison between original and MDO optimized rotor 67
A 3D geometric parameterization for transonic fan blades is proposed to serve as a central parametric model in an integrated blade design system. The proposed parameterization uses physically relevant engineering parameters, i.e. blade angles and thickness distributions, to provide an easy link with the experienced designers. The parameterization keeps a section by section description of the blade, and adds a smooth span wise variation of the section parameters to help controlling the blade shape. In addition, a multi-level modification approach is proposed in order to reduce the number of Parameters by linking groups of control points through a Gaussian influence function.
The parameterization was validated by the replication of the NASA Rotor 67 to show its accuracy. The proposed parameterization replicated very well the reference blade by conserving the efficiency and total pressure ratio with very small differences. The new 3D geometric parameterization has then been placed at the center of a multi-disciplinary design system and examples are provided of its successful application to optimize the efficiency of the Rotor 67 while respecting multidisciplinary constraints. More complete results for the blade optimization will be provided in a future work.
None.
Author declares that there is no conflict of interest.

©2017 Trepanier, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.