eISSN: 2576-4500


The objective of this paper is the development and application of a methodology for preliminary analysis of variable pitch fan (VPF), both as a separate component and as a module integrated into a short-medium range geared turbofan engine developed within European FP7 project ENOVAL. For this purpose, a high bypass ratio two spool geared turbofan engine model was constructed in software PROOSIS. A VPF performance modeling methodology was then developed using 3D steady RANS CFD produced fan maps as baseline; the CFD maps characterized five discrete fan pitch angle settings. In order to represent those maps in PROOSIS and add the pitch angle as a degree of freedom, they were transformed into the Map Fitting Tool (MFT) reference frame. Once the complete VPF turbofan model was in place, engine mission optimization experiments were carried out. The resulting performance is characterized by a good capability to control the fan surge margin, without degrading the engine fuel consumption. This paper represents a new contribution on the topic firstly by coupling a 0D engine performance code with a 3D RANS calculation, and then by introducing the concept of MFT maps with an additional degree of freedom as the interface between the two.
BPR = Bypass ratio
CFD = Computational Fluid Dynamics
MFT = Map Fitting tool
Nc = Corrected rotational speed
OPR = Overall pressure ratio
PR = Pressure ratio
SFC = Specific fuel consumption
SM = Surge margin
SMN = Surge margin at constant rotational regime
TRL = Technology readiness level
VPF = Variable Pith Fan
Wc = Corrected mass flow
π = Pressure ratio
η = Efficiency
When describing the fan module in particular, recent tendencies in the civilian aeronautical propulsion industry could be looked upon from two perspectives. Aiming at reducing engine thrust specific fuel consumption, the first and foremost tendency is to go towards higher bypass ratio engines, with the so called Ultra High Bypass Ratio (UHBR) engines, characterised by bypass ratio of up to 20. The reason for this can be deduced from the basic turbofan analytical considerations which show that the engine SFC decreases with increasing bypass airflow. Simultaneously, for a higher propulsive efficiency of the engine, it is of interest to reduce the bypass ejection speed, or consecutively the fan pressure ratio (PR).1 Another typical trend in the European research to consider here is study of variable thermodynamic cycles in order to adapt the engine behaviour to various operating points during the mission. For this purpose, devices that enable variable geometry and thermodynamics have been studied in the recent years, for example within European project E-BREAK.2 The two outlined tendencies cross over in a European FP7 project ENOVAL task which deals with low pressure system of the civilian engines. In this context, the task investigated variable pitch fan (VPF) module as means to control engine operability i.e. fan surge margin. It was shown that the variable pitch fan could be used for manipulating the relative position between the operating line and the fan surge line. The left part of Figure 1 illustrates the displacement of the low PR fan operating line towards the surge zone as a consequence of decrease in Mach number (e.g. at takeoff). To remedy for this behaviour and increase the surge margin, the map itself can be displaced relative to the operating line by means of a variable pitch fan (Figure 1, right).3 This comes as an attractive feature if the previously mentioned trend to reduce fan PR is taken into account.
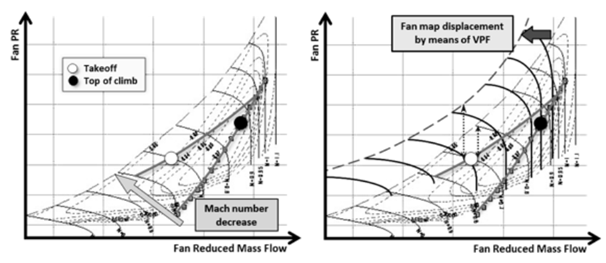
Figure 1 Fan operating line displacement at low Mach numbers (left); displacement of fan map using VPF (right).3
Bensimhon3 shows that low PR fans have poor stability at lower rotational regimes at low Mach numbers, as the operating line moves away from the critical line (which indicates the limit of choked flow); this applies at low Mach number flight cases such as takeoff and landing (Figure 1). The same author shows that a solution to avoid this problem would be a fan with variable pitch blades, which would allow a possibility to actively control the fan SM-either to reduce it if it is unnecessarily high in favour of a potential efficiency benefit, or to increase it in situations of particular relevance in terms of safety, e.g. takeoff or landing with cross wind. Different VPF turbofan technologies were produced throughout the years. VPF equipped turbofan called Astafan, which aimed at improving the fuel efficiency by running at constant rotational speed was developed by Turbomeca. Its first prototype test run was in 1969, it was being developed until the late 1980s, but it was ultimately never produced commercially. Early 1990s saw the development of Advanced Ducted Propulsor (ADP) by Pratt Whitney and NASA. As opposed to Astafan, ADP mounted a VPF on a turbofan for noise reduction purposes.4 Most recently, Rolls Royce announced development of a VPF equipped turbofan called UltraFan, possibly entering into service by 2025. According to Haselbach et al.,5 UltraFan VPF module would enable optimal low pressure fan operability, as well as the elimination of the need for a thrust reverser.
Despite the idea of a VPF turbofan being far from new, no references were found in the literature on modelling such a technology at a complete engine level, as opposed to the fixed fan geometry engines, which is commonplace. It was therefore relevant in the first place to identify fixed fan calculation methods that could be extended to accommodate the additional degree of freedom (fan pitch). When fan performance is discussed, standard methods to produce the data are either experimental or numerical (CFD). Given that the current fan/engine technology is at a low TRL and 3D steady-RANS approach was identified as sufficient for producing fan performance data. In order to integrate this fan behaviour into a complete engine cycle, software PROOSIS was used. PROOSIS is a European-developed object oriented software dedicated to turbomachinery system modelling, developed within EU project VIVACE. For more details on PROOSIS, see Alexiou & Tsalavoutas.6 In terms of fan, compressor and turbine modelling, PROOSIS default components are only capable of representing the configurations without variable geometry, through generic component maps. Zarati et al.,2 used PROOSIS to explore variable cycles enabled by variable nozzle areas, but no work that dealt with variable turbomachinery rotor geometry was found. PROOSIS users are enabled to insert their own component maps. The performance map of turbomachinery components such as fan can be represented in a frame of reference based on work and loss coefficients, rather than the standard one ( π-Wc-η -Nc). This frame of reference, called MFT (Map Fitting Tool), was developed by NASA, and presented in Converse & Giffin.7 MFT came forward as relevant because it is extensively used in PROOSIS components; a presentation is available in Sethi et al.8 Moreover, since MFT is about an analytical representation of the maps, expressed by a series of physical parameters, it can be used first of all to complete a map by interpolation, and where needed extrapolate performance to very high or very low speed regimes. With this capability, MFT becomes an obvious choice for being extended by the additional degree of freedom (pitch angle), in order to provide a modeling capability.
The objective of the study is twofold, and it is reflected directly through the structure of this paper. The primary objective is to develop a comprehensive engine performance simulation platform adapted for analysis of a VPF equipped turbofan; this will be presented in Section II of this paper. For this purpose, it was envisaged to develop a PROOSIS model (subsection II A) whose input on VPF performance would come from dedicated CFD studies (subsection II B). Subsection IIC will introduce the "MFT" reference frame for the fan map, which allows for integrating the CFD results into the engine system modelling software. The secondary objective is to apply the developed methodology along a typical turbofan mission in order to validate the platform operation and to obtain a first idea of how VPF impacts the fan SM operability and fuel performance of the current engine. Section III contains the description and setup of the performed studies; it is followed by sections on discussion of the presented elements, and a conclusion. This paper represents a new contribution on the topic of variable geometry turbofan engine performance analysis firstly by coupling a 0D engine performance code with a 3D RANS calculation, and then by introducing the concept of MFT maps with an additional degree of freedom (pitch angle) as the interface between the two.
Turbofan engine cycle modelling in PROOSIS
The engine selected to be equipped with a VPF module was a short-medium range geared turbofan, designed to power an A320-type aircraft. In order to simulate the engine cycle, system modelling software PROOSIS6 was used. The baseline cycle specifications, that is, for the cycle with fixed geometry fan, were provided for three operating points (Takeoff, Top of Climb and Start of Cruise) by Safran Aircraft Engines (Table 1). Given that the high pressure and low pressure core performance maps were a priori unknown, the essential part of the cycle design procedure was the map scaling. In order to calculate the map scalars, a multipoint design procedure was carried out.9 The merit of multipoint design is the capability to take into account constraints that characterize different flight points defined by the user. As a result, the obtained map design (i.e. map scalars) is still unique; however, as opposed to the single point design, it is optimized for all the defined mission points. For the current case, three mission points were used. They were defined, along with their constraints, as follows:
Parameter |
Unit |
Take off |
Top of climb |
Start of cruise |
Net thrust |
N |
85768 |
22442 |
19363 |
BPR |
- |
15.9 |
15.5 |
16.2 |
OPR |
- |
46.1 |
54.7 |
50.4 |
Table 1 Selected performance parameters of the baseline engine cycle
The engine schematic constructed for setting up the reference cycle is presented in Figure 2. The engine architecture consists of a high pressure core and a low pressure core linked to the fan by means of a gearbox. All the cooling air for the high pressure and low pressure turbine is taken at the high pressure compressor level. The core and the bypass flows are unmixed, i.e. each flow leaves the engine through a separate nozzle. As previously explained, performance of all the turbomachinery modules of this engine is described by scaling generic component maps in order to match the desired engine design points. This is not the case for the VPF module, because despite having all the necessary capabilities available (e.g. steady, transient, mission analysis) - the crucial drawback of PROOSIS for this project was its lack of capability to represent variable geometry turbomachinery. For this reason, it was necessary to find a way to extend the default PROOSIS component functions in order to take into account the additional degree of freedom of the fan rotor pitch angle. If Reynolds number and γ effects are neglected, compressor performance variables, i.e. performance map, are a function of compressor geometry design only.1 For this reason, the next step in the VPF modeling was to produce a series of fan performance maps for discrete rotor pitch angles, and at a later phase attempt to reintroduce thus described fan performance into PROOSIS for complete engine analysis.
Fan performance: CFD maps
For purpose of this task, Safran Aircraft Engines provided a complete VPF stage description. Computations on this geometry were performed using the commercial code NUMECA FINE/Turbo. It solves the steady three dimensional Reynolds Averaged Navier-Stokes equations based on a cell centered finite volume approach on structured grids. All the numerical parameters mentioned below have been set according to previous study10 that was performed on a similar axial fan and which showed good agreement between experimental measurements and numerical data. The spatial discretization was a central scheme with a Jameson11 type dissipation using 2nd and 4th order derivatives of the conservative variables. Time integration was performed with an explicit four-stage Runge-Kutta scheme. Conventional techniques as multigrid method, local time step, smooth residual stepping were used to speed up the convergence of the simulations. The turbulence model used for performing the simulations is the single equation model Spalart-Allmaras.12 The numerical domain consisted of an inlet region, spinner, rotor, outlet guide vane, and the two exit domains (core and bypass). The Figure 3 represents a meridional view of the calculation domain. The distance between the inlet of the calculation domain and the inlet of the spinner is equal to two rotor blade chords. The structured grid was created with Autogrid V5 and is discretized using H and O topologies. The size of the first cell was set to 1µm and lead to y+ < 1 near wall regions to allow a good description of the viscous effects and turbulent gradients. The domain point distribution and number of nodes are summarized in Table 2.
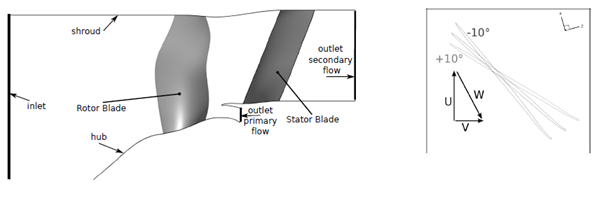
Figure 3 Meridional view of CFD numerical domain (left); Rotor blade pivoting visualization (right).
|
Number of points |
Radial direction |
Axial direction |
Azimuthal direction |
|
Rotor |
141 |
135 |
73 |
|
Stator |
105 |
169 |
67 |
|
Total number of points |
INLET |
ROTOR |
STATOR |
|
0.334*106 |
2.668*106 |
1.596*106 |
Table 2 Number of points of the fan stage numerical domain
To reduce computational cost, only one blade passage per blade row was taken into account in the numerical domain. The interface between the rotor and the stator is treated with the classic mixing plane approach. Five chosen pitch configurations have been calculated: -10°, -5°, 0°, +5° and +10°. All the configurations have the same mesh characteristics in terms of number of points distribution. Considering the boundary conditions, the total pressure, the total temperature and the flow angle (axial flow) were precscribed at the domain inlet. At the primary duct outlet, a mass flow value was imposed. This value was constant all over the constant rotation speed but changes with the rotation speed. Considering the outlet boundary condition, the characteristic curve representing the total-to-static pressure ratio of the fan depending on the mass flow may have a positive slope at
low mass flow rates. Then, a static pressure condition is not adapted as two solutions with different mass flow rates are possible. To accurately simulate the part of the curve having a positive slope, the bypass outlet boundary condition was modeled using a throttle condition. It means that the outlet static pressure imposed by the solver depends on the mass flow rate. The imposed pressure was prescribed according to the following equation:
is the mass flow rate at the outlet. The reference pressure Pref was set to 101325 Pa while the reference mass flow ( ) was set to 668kg=s representing the design operating point mass flow. These values were chosen arbitrarily. This boundary condition permitted simulation of different operating points from choke to stall by simply increasing the value of . The blades, hub, and shroud walls were treated with a no slip adiabatic condition. For all five configurations, performance maps were defined with 8 iso-speed lines, ranging from 50% to 105% of the nominal rotation speed. For each iso-speed line, the outlet boundary condition was modified to simulate the complete operating range from choke to stall. To correctly describe the near stall region, the value of the boundary condition would be slightly increased. When the value increases, the mass flow of the simulated operating points decreases. When the value becomes too high, the simulation does not reach a steady state. It would then be considered that stall region was reached. This method was applied for the 8 iso-speed lines and for the 5 configurations. This set of calculations has provided what was considered to be a complete performance map. The resulting maps for the 5 pitch angles are presented in Figure 4. The following step is integrating these performance maps into PROOSIS. However, they firstly need to be transformed into the format comprehensible by the software, which is the subject of the next section.
Transformation of the maps: map fitting tool (MFT)
PROOSIS turbomachinery components use two types of maps: the Beta maps, described in standard reference frame, and the MFT maps. For various reasons that will be outlined in the following, MFT was adopted as the frame of reference for the current map, which is why a transformation needed to be carried out prior to integrating the resulting maps into the engine model. The MFT methodology takes description of the given turbomachine work and loss coefficients as the starting point for defining its reference frame. Namely, for each iso speed of a fan or a compressor, a relationship between the work and loss coefficients can be identified, or equivalently, each iso-speed line of the map can be represented in terms of the work (GH) and loss (GL) coefficients. In that frame of reference, the iso speed line takes a parabolic shape. When presented in this manner, it is clear that each iso-speed line is characterized by work that results in minimal losses. When these minimum loss points are identified for all the speed lines, they give basis for the so called backbone line of the compressor map. In other terms: if the compressor operates along the backbone line, it will be working with minimum losses. Compressor map points are thereby represented in terms of their offset from the backbone line. For more details on the MFT map parameters, and their relation to the standard map parameters.7,8 In order to transform the five maps, the following input data were required:
It is of utter importance to have smooth evolutions of all the MFT parameters used in the modeling as a function of the rotational regime. Consistency of the five maps transformation was of utmost importance because the goal was to compile a comprehensive map whose above outlined characteristics would be presented with the additional degree of freedom. The analytic relationship of the MFT parameters is crucial because it enables interpolation and extrapolation of the curves in order to complete a map. Taking into account that CFD calculations of a complete performance map can be time consuming, this sort of capability can be very useful for extending the available operating range of the given component. As shown previously, the five discrete pitch angle maps were spanning from 50% to 105% of the nominal rotational regime with a 5% step between 90% and 105%. In order to accommodate any potentially higher rotational regimes that might occur in the subsequent PROOSIS calculations, this range was extended/extrapolated with two additional speed lines: 110% and 115%. Finally, for the five performance maps obtained numerically, the surge line is defined by taking the maximum pressure ratio of each rotation speed characteristic curve. In other words, even if the characteristic curve has a positive slope at low mass flow rate, this part is not taken into account (see +10° map in Figure 4). The final variable pitch fan engine modeling procedure, described as an assembly of different previously outlined modeling units, is presented in Figure 5.
Engine mission
The developed methodology was applied on a mission analysis. In PROOSIS, a mission is constructed using time laws of thrust and flight conditions as input. A typical mission data for the current engine was obtained in the ENOVAL project context. This mission profile is illustrated in Figure 6 with time evolutions of net thrust and flight conditions, nondimensionalised by their respective values at top of climb (Table 3). When discussing the engine mission at hand, a particular limitation of the model must be pointed out. While constructing the cycle and exploring its characteristics through parametric studies, it was observed that the obtained cycle could not operate below roughly 80% of the nominal fan rotational regime (Figure 7, left). A possible explanation of this behavior was that the best obtainable high pressure compressor map that could be provided for the purposes of this project (for confidentiality reasons) did not sufficiently match the great rotational speed discrepancy between the low pressure and high pressure core, which characterizes the engine cycle at hand. For this reason, the approach and landing phases had to be omitted from the final simulation, since mission calculations failed at the top of landing, when attempting to reach low rotational regimes on the fan map.
|
Altitude |
Mach number |
Net thrust |
Top of climb |
1000m |
0.78 |
22300N |
Table 3 Top of climb flight conditions for the current engine mission
The final baseline mission (baseline being with the fan geometry fixed at 0° pitch) represented by the fan map operating line is shown in Figure 7 (right). In order to avoid redundancy, the calculated baseline fuel burn will be presented in Table 4, where it will be compared to the fuel burned by the optimised cycles. The part 1 of the table presents the results from the mission calculation where the fan SM was being kept at constant value of 10%, whereas part 2 shows the equivalent results of the SFC optimization study with the condition of fan SM < 10%, for the entire mission. The corresponding fan surge margin time evolution is given in Figure 8. The surge margin parameter that was considered in this work is the surge margin at constant rotational regime, denoted by SMN. As it can be seen in Figure 8, the baseline fan surge margin is characterized by low SM of 7 to 10% at the very early takeoff, and high SM peaking at 15% during climb, which levels out at around 13% during cruise. From this baseline trend, the interest in VPF in terms of fan SM was identified:
Part 1 |
Baseline |
Optimized |
Δ[kg] |
Δ[%] |
Complete mission |
6639.1kg |
6639.4kg |
+0.3 |
+4.5*10-3 |
Takeoff and climb |
290.0kg |
294.8kg |
+0.8 |
+0.27 |
Part 2 |
Baseline |
Optimized |
[kg] |
[%] |
|---|---|---|---|---|
Complete mission |
6639.1kg |
6631.6kg |
-7.5 |
-0.11 |
Takeoff and climb |
290.0kg |
294.0kg |
0 |
0 |
Table 4 Baseline fuel burn compared with the results from the two cases
VPF optimization studies
As mentioned in the modeling section, the second part of development work in PROOSIS consisted of expanding the existing component equations, functions and tables in order to accommodate the additional variable, fan rotor blade pitch. The principal aspect consisted of assembling a coherent VPF MFT map file, which encompassed all the five individual CFD maps transformed into MFT. The rest of the work would then consist of expanding the PROOSIS interpolation functions to use the pitch as an additional interpolation parameter. Additionally, this enabled construction of optimisation experiments where the fan pitch could be used as a decision variable. Additionally, the optimisation experiments had to be assembled to enable mission optimisations with pitch angle as the decision variable. In practice this was performed by using the existing single point optimisation capability of PROOSIS combined with the mission calculation presented in Figure 7 (right). An illustration of single point optimization done in PROOSIS, with fan pitch as the decision variable, is
presented in Figure 9. Due to PROOSIS limitations, a fan map cannot be plotted for a variable pitch case, which is why the π-W was plotted separately (Figure 9, far right). The basic outline of the developed mission optimisation experiment is summarized as follows:
In this manner, this study was split in two parts, with their respective objective functions given as follows:
In practical terms, the goal of Part 1 was to observe the VPF engine behavior if the SMN was to be kept at a fixed value (10%) during the whole mission. The goal of Part 2 (Optimization) was to assess how much the engine SFC can be further optimized while not allowing the SMN to go below.
The relevant results of the two optimizations, compared to the corresponding baseline mission performance are illustrated as a function of mission time in Figure 10, and are discussed in the following. The reader is reminded that the baseline performance was obtained with the CFD fan map at the nominal (0°) pitch angle. Also note that the mission time on the x-axis in Figure 10 is truncated at t=1200s to improve the clarity of the visualization. In fact, no significant variation of the presented parameters is observed after this time, which justifies this particular focus on takeoff and climb. For the baseline mission (see Figure 10) where no fan pitch angle variation is considered, the fan SM is higher than 10% except at the early takeoff where its value drops up to 8% (Figure 10b). Part 1 aims at keeping a constant SM value of 10% (Figure 10b), which could mean a reduction of up to 35% relative to the baseline (Figure 10c). To obtain this constant value of SM, the fan pitch angle should be increased up to approx. +3°; on the other hand, at the early takeoff it should be reduced up to -2° (Figure 10a). All intermediate pitch angle variations take place between these two angle values. Compared with the baseline, the consequence is a small increase of SFC: up to 0.4% during the first 700s (except during early takeoff where SFC can be reduced up to -2%) and up to 0.1% during the rest of the mission. In terms of the fuel burnt during the mission, the consumption increase is negligible. (Table 4) When it is sought to optimize the SFC with keeping the SM equal to or higher than 10%, the Part 2 (SFC optimization) demonstrates that there exists some improvement space.
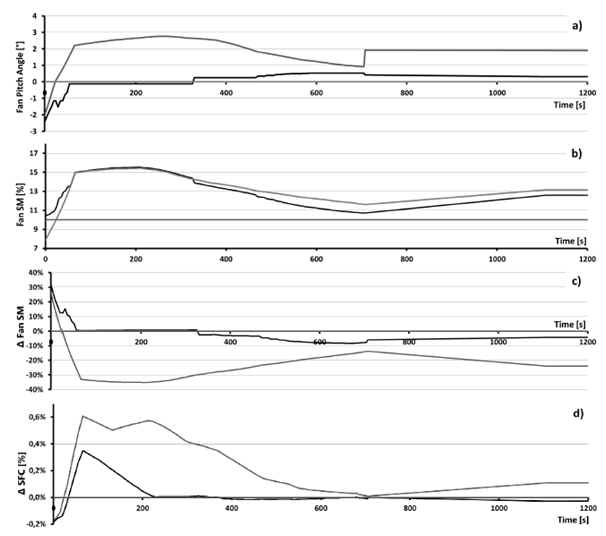
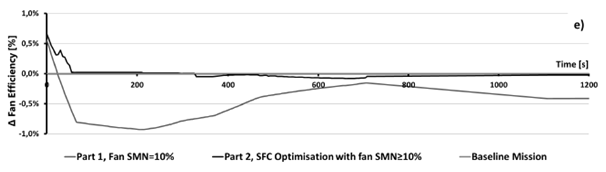
Figure 10 Parameters time evolution resulting from the two studies, compared to the baseline mission.
In fact, Fig.10d shows that the SFC can be largely reduced during the takeoff and climb phases, compared to Part 1. Thus optimized SFC value remains slightly lower than the baseline during the rest of the mission, i.e. from approx. t=1000s, all the way until the mission end at t=26580s. This minor SFC improvement (in other words, very close to the baseline value) is intuitive, because the baseline cycle is designed in order to operate with optimal SFC during the cruise. Furthermore, when this SFC reduction relative to Part 1 is attained, a re-increase of the fan SM is observed (Figure 10b). One remarks that in this case, where the SFC is optimized, it is possible to remain at a SM value higher than the baseline one during the takeoff (Figure 10b). For this optimization the fan pitch angle varies between -2° and +0:5° (Figure 10a). The same way as it had been found in Part 1, the global impact of the Part 2 optimization on the fuel burn is negligible (Table 4). It is pointed out that an anomaly was observed in terms of the SFC behavior (Figure 10d), notably between t=50s and t=200s where the fan SM did not change relative to the baseline (Figure 10b), but some degradation of the SFC took place nevertheless. This anomaly is of additional interest since no significant change in fan efficiency was observed during this time period (Figure10e). The question of how an SFC minimization optimization actually led to its increase remains open for the time being, and will be investigated within a further continuation of this work. Nevertheless, even if it had behaved as one might have expected (no change relative to the baseline, or a slight reduction), it would not have had a major impact on the mission fuel burn reduction, which at this moment is -7.5kg. (Table 4) On the whole, it is observed that the main interest of VPF is the possibility to increase the SM during early takeoff, and during the rest of the mission, it is possible to reduce the SM value if necessary. Although the fan SM can be controlled successfully, the VPF does not seem to be capable of providing a simultaneous improvement in the engine SFC. Simultaneously, this does not come as a disadvantage, because it was also observed that the SM control capability does not have a deteriorating impact on the engine fuel burn.
VPF was identified primarily as a candidate to ensure a continuous engine safety for nominal configurations characterized by high engine BPR and low fan PR, which would imply compromised fan surge stability at low Mach numbers. For UHBR engines the fan will generate the majority of the thrust, which is why the necessity for continuous fan stability is essential. From the performed work carried out by means of a methodology that combines system modeling in PROOSIS with CFD calculations, it can be seen that VPF can meet the fan surge margin control necessity, in this particular case illustrated by fixing it at prescribed value of 10% throughout the entire mission. Furthermore, the predicted VPF control seems to imply no penalties in fuel burn (calculated through SFC only), which is an important constraint for the contemporary civilian engine industry, as well as the future developments. For a comprehensive conclusion, it remains yet to be seen how a VPF would impact the safety and fuel performance during the approach and landing phase of the mission, which was not possible to simulate during the current work due to technical limitations. Moreover, at a later phase the presented conclusion on the VPF usefulness in terms of operability and fuel burn would necessarily have to be compared to other technological aspects that are not discussed here, such as system integration, structural complexity, reliability and maintainability, additional drag and added weight. From the performance and fan stability analysis perspective, further course of action which would solidify and complement the findings presented in this paper should take into account the following few guidelines:
The work presented in this paper was carried out within the framework of European Union project ENOVAL (Engine Module Validator), funded by Seventh Framework Program under Grant Agreement no. 604999. The authors would also like to acknowledge the support provided by Safran Aircraft Engines and Empresarios Agrupados.
Authors declare that there is no conflicts of interest.

© . This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.