This paper introduces a 1U CubeSat based on 3D printing technology. Compared to the traditional large satellites, CubeSat has advantages such as low cost and short development cycle, so more and more CubeSat has been applied to space exploration missions in recent years. The design process of the CubeSat includes the determination of main parameters, the design of external and internal layout, and the structural main features. To professionalize the engineering work of CubeSat design, the concept of design process is proposed, and the structure and parameter optimization (SPO) about basic parameters and feature compatibility are found. The design problem is solved gradually by the structure and parameter optimization (SPO), and the value range of the selected parameters is determined. In this paper, a CubeSat prototype manufactured using 3D printing technology, having this several advantages including fast implementation, accuracy in manufacturing small parts and low cost, the combination of CubeSat and 3D printing technology will maximize the rapid development of CubeSat. In the space exploration field, the number of 3D printed plastic CubeSat is very small, and this paper is aimed to test the ability of the plastic CubeSat to complete space exploration missions in space. In this paper, the 3D printing technology and traditional manufacturing technology are discussed, and the feasible structure design model is obtained by combining the material and parameter design.

Keywords: CubeSat, 3D printing technology, structural design, parameters, structure and parameter optimization (SPO)

Space exploration has always been an important area of scientific exploration, which used to be conducted through large traditional satellites. By the end of the last century, space exploration devices were gradually developing toward miniaturization, such as Small Spacecraft (SmallSats). SmallSats consist in Spacecraft with the mass under 500 kilograms.¹ According to the mass and size, SmallSats can usually be divided into the following²: Minisatellite, 100-500kg; Microsatellite, 10-100kg; Nanosatellite, 1-10kg; Picosatellite, 0.01 1kg; Femtosatellite, 0.001-0.01kg (Figure 1). In the last two decades, the scientific community began to use CubeSat to complete some space exploration missions. CubeSats advantages are represented by their low cost and short development cycle compared to traditional large satellites, and they can be used as a secondary payload for rocket launch due to its small size, which greatly reduces the launch cost.³ STU-2 and Athenoxat-1 are two LEO (Low Earth Orbit) CubeSats. The mission of STU-2 is to carry out Earth observation for polar region icing situation, with an on-board optical camera.⁴ Athenoxat-1 is launched to demonstrate the functionality of multiple optical payloads in orbit.⁵ The Lunar Polar Hydrogen Mapper (Lunah-Map) is a beyond LEO CubeSat mission, which will complete low perilune (10km) passes over lunar south pole to map hydrogen abundance and distribution in PSRs.⁶ Considering the harsh working conditions in space, such as radiation, extreme heat cycles, and low pressure, the CubeSat mission results a very challenging task in terms of these factors. In addition, the reaction force during launch process also requires the CubeSat to have good impact resistance.⁷ To meet these requirements, the most common solutions are metal materials and traditional manufacturing techniques, such as sheet metal processes.

Figure 1 Overview of the mass range of SmallSat.¹

This research made a new attempt, combining CubeSat manufacturing and 3D printing technology, and using PLA (polylactic acid) as a material for the structure realization of the CubeSat. The 3D printing technology has the advantages of rapid realization, high precision of manufacturing small parts and low cost. The combination of CubeSat and 3D printing technology will maximize the rapid development of CubeSat. It is easy to achieve the goal of lightweight with PLA (polylactic acid) as the structural material. At present, the number of CubeSat designed with plastic materials is very small, and the design scheme proposed in this study will open a new road in the manufacturing technology of CubeSat. In the design process of this research, the first main problem is to determine the value range of the key structural parameters by combining the concept of system calculation. Secondly, combined with the discussion of manufacturing technology, the design scheme of CubeSat structure was proposed. By comparing several feasible schemes, the best design scheme was obtained, and preliminary model manufacturing was carried out.

The specialization of CubeSat development projects usually involves the following issues:^1,8

1. Design and strength checking calculations (design and calculation works);
2. Mass, momentum of inertia calculations, the center of mass position and positions of the main inertia axes (modeling);
3. Thermal calculations (computer analyses).

Decomposed a complex problem into multiple secondary problems is a method to solve the above listed issues. At the same time, to ensure the convergence of the internal cycle of the structural design process and the consistency of levels and levels in the decomposition scheme, it is advisable to use the procedure of structure and parameter optimization (SPO) accepted in the design theory for complex technical systems, which is to be used to estimate design versions based on the properties. Than can deliver the object with the optimum combination of the parameters in the compared structures. The engineering design solutions (EDS) can be presented at each level of the complex of the essential features in two adjacent levels:⁹

$x_i={\tilde{x}}_i+{\tilde{x}}_{i+j}$ (1)

In this case, are the structural features, and are parameters of the structure of i - level of decomposition. A complete Multilevel SPO Diagram should be like Figure 2. Any design technology needs to be integrated with the typical development state of the product and conform to CubeSat related technical specifications. Therefore, in the design process of CubeSat, the basic parameters of structure design should meet the premise of technical specification.

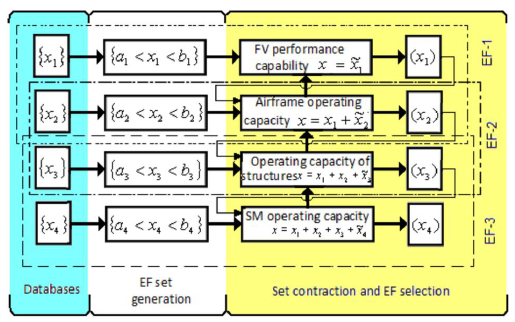
Figure 2 Multilevel SPO diagram for FV (EF - essential features).⁹

The study of physical relationships during design process is necessary. The first task is to find some optimal design solutions about compatibility of basic parameters and characteristics of CubeSat.¹⁰ This problem be solved by the Multilevel SPO Diagram method in the previous section. The second of the tasks set is to search for optimal combinations of parameters and characteristics. It is much more difficult than the first one. This is mainly due to the complexity of studies of this sort of tasks.¹¹ In the simplest case, the initial weight of the CubeSat $M_0$ suitable for the launch vehicle needs to be determined. In this case the weight of the equipment $M_{Sc}$ will be

$M_{Sc}=M_0-M_{ss}$ (2)

where $M_{ss}$ is the total weight of the service systems, frame and on-board cable network necessary to ensure the operation of the spacecraft. Thus, in the simplest case, when the launcher is specifying, the task of rational design is reducing to minimization of the total weight of the frame with service systems and the on-board cable network. In this case, the initial weight of the vehicle $M_0$ can be considering as design value. For the cases when the value $M_{ss}$ in the expression (2) cannot be considering independent the value , $M_{Sc}$ it is possible to write the following:¹²

$M_{Sc}+f_{ss}{M}_{Sc}=M_0-M_{Sc}{}^0$ (3)

instead of the specified expression, where $M_{Sc}{}^0-$ is the total weight of the service systems and the frame independent of the weight of the scientific equipment; $f_{ss}{M}_{Sc}-$ is an additional weight of the service systems and the frame, necessary for operation of the scientific equipment depending on its weight, composition and operation program. If the function $f_{ss}{M}_{Sc}$ is quite simple, the expression (3) can be solving relative to the value, $M_{Sc}$ i.e. find the expression

$M_{Sc}=F(M_0,{{\displaystyle M}}_{ss}^0)$ (4)

In this case, the maximum value can be searched directly $M_{Sc}$ .

For seeking a minimum of the value ${{\displaystyle M}}_{ss}^0$ in the expression (4), i.e. neglect the weight of the scientific equipment, it also can be approximate, as the versions of the service systems disregarded in the design process can provide a smaller value $f_{ss}{M}_{Sc}$ than the chosen versions.¹² To indicate the probability of flawless operation of the spacecraft within a specified time $t_0$ as B, it can be written as:

$B=B\left[\left(C_{m,n}\right),\left(T_i\right),\left(P_j\right),t_0\right]$ (5)

where $\left(C_{m,n}\right)-$ is the finite set of basic parameters of systems; $m-$ is the system number; $n-$ is a parameter number; $\left(T_i\right)-$ is a parameters set determining the trajectory of the spacecraft; $\left(P_j\right)-$ parameter set determining the operation program. The probability of CubeSat flawless operation shall be determined by the reliability of its individual systems. It can be noted that the minimum number of CubeSat corresponds to the minimum cost of solving the problem or the minimum time to complete the entire program. These expressions will include some constants. These equations and inequalities shall be writing as follows

${\Phi }_r\left[\left(C_{m,n}\right),\left(T_i\right),\left(P_j\right)\right]\{{}_{\ge 0,}^{=0,}$ (6)

where $N=1,2,\mathrm{.....},N_m;$ $N_m-$ is the number of basic parameters of the $m-th$ system; $m=1,2,\mathrm{......},M;$ $M-$ is a number of on-board systems; $i=1,2,\mathrm{...},I;$ $r=1,2,\mathrm{...},R;$ $j=1,2,\mathrm{...},J$ . If all the expressions (6) are equations and, $R<N_{\Sigma }$ , then the task of seeking for optimal parameter values is confining to finding a constrained extrema of the many variables function. The relations of type (6) are simultaneously the constraint equations.¹³ The purpose of rational design is to create a project of a CubeSat for which the value of the selected criterion is close to the maximum or minimum value. In this case, different configuration diagrams and different orientation schemes¹³ should be considered. It depends on the versions of design solutions and the functions K and $\Phi$ . Consequently, the rational design shall be limited to the investigation of the function K in the constraint equations (6) for different versions of the newly designed CubeSat.

The first task of structural design is to choose model. Figures 3-5 shows some collected CubeSat structures. Fig. 3 presents a relatively outdated CubeSat model,¹⁴ and, it was completing in 2008. Its overall weight is no more than 1 kg, but the metal shell takes up a lot of weight, which means the CubeSat cannot carry many payloads. It is clearly that a larger payload is better. Such a design runs counter to the goals, so this outdated design was not adopted.

Figure 3 CubeSat model.¹⁴

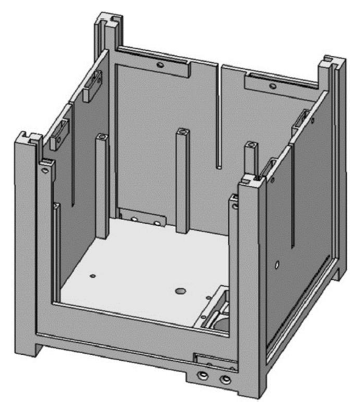
Figure 4 Plastic CubeSat structures.¹⁵

Figure 5 A lightweight CubeSat model (PICASSO).¹⁶

Figure 4 and Figure 5 shows two clearly advanced designs,^15,16 the side panels can be separated from base, and such design has the following advantages:

1. The removable side panel means that internal circuit board and satellite payload can be placed easily.
2. Owing to the side panel and the base is not whole, different materials can be used. For example, the base, which with the high strength requirement, a metal or a composite material will be appropriate; and for side panel part whose strength requirement is not high, some lightweight materials (aluminium or plastic) will achieve the purpose of saving weight.

After summarizing all the structures investigated, the following structural design (Figure 6) was proposed. This is a structure consisting of two identical top and bottom plates, four equal sides, and eight identical bases. Such of design would greatly simplify the manufacturing process of the structure. Moreover, such design idea is conducive to the installation and disassembly of the whole structure. At the same time, the interior of the structure was made as large as possible to carry more payload. The design of the side panel is to reduce the quality under the premise of ensuring the structural strength. In the design process of the whole structure, another alternative design also has been proposed. It is the plan B structure (Figure 7). It also has some advantages, such as reducing the quality of the side panel, can be expanded in all directions, etc. Compared with the structure chosen above, one of the biggest differences is that it is composed of a whole formed by one base (Figure 7) plus side plates. However, this plan B structure has some redundant parts; it also takes up the CubeSat payload quality. In addition, all six of its sides are just bolting in the base, rather than embedded as the design chosen above, which means the design intensity is significantly worse. The most important point is that considering that the structure manufacturing will be realized through the 3D printing FDM (Fused Deposition Modeling) technology, Plan B structure implementation will have many redundant support structures, and the clearance work is complex. Therefore, the plan B structure was used as a backup.

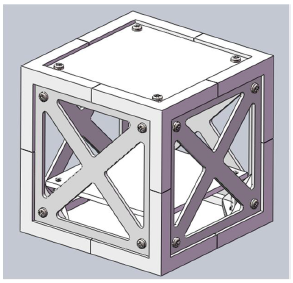
Figure 6 Completed structure design.

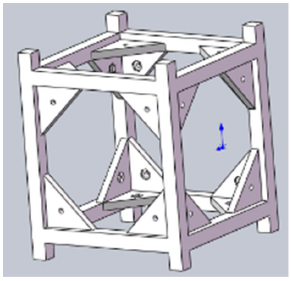
Figure 7 The base of the plan B structure.

Considering the harsh working conditions in space, such as radiation, extreme heat circulation and low pressure pose great challenges to the work of the CubeSat. In addition, the reaction force generated during the launch process also requires the CubeSat to have good impact resistance. Common solutions are metal materials and traditional manufacturing techniques, such as sheet metal technology. In the design process, a version of the CubeSat structure with sheet metal technology was built as well (Figure 8).¹⁷ Such traditional manufacturing methods usually have the characteristics of high strength, smooth surface, heat and radiation resistance, which can meet the requirements of space working environment. However, there are also some defects, such as high production cost. In addition, the production cycle of traditional manufacturing technology is relatively long, which conflicts with the short-term research and development goal of CubeSat mission. Compared with traditional manufacturing technology, 3D printing technology is more suitable for the manufacturing of CubeSat.¹⁷ The 3D printing technology has the advantages of fast realization, high manufacturing accuracy and low cost, and compared with the traditional manufacturing technology, it can achieve high accuracy in detail. In addition, the advantage of 3D printing technology is that it can produce products with very complex shapes, which are usually impossible to achieve in a low-cost form or in a short time with traditional manufacturing methods. The traditional manufacturing process is to remove the material, while 3D printing is to cover the material layer by layer, which is also known as FDM (Fused Deposition Modelling) technology. In the process of covering, if the suspended structure appears, it will appear redundant structure to support the cover. According to the characteristic analysis of FDM technology, if the designed structure is unreasonable and there are many suspension structures, there may be a lot of redundant support structures or even lead to manufacturing failure. Figure 9 shows an unreasonable structure designed before. However, the structural design of Figure 6 avoids the problem successfully by splitting the whole into multiple parts. The preliminary printing product is shown in Figure 10.

Figure 8 CubeSat structure with sheet metal technology.

Figure 9 A failed structural model.

Figure 10 The preliminary printing structural model.

This research work summarizes CubeSat technology, provides examples of their scientific impact, and describes the design and the manufacturing of a CubeSat platform. The CubeSat design process is comprised of choice of its trajectory, determination of components and main parameters, systems, development of external and internal layouts, determination of the number of satellite-born antennas and their main characteristics. Proposed paper will focus on estimating a concept and physical relationships in the design process, and on the rational design algorithm version. In terms of specialization of engineering works during CubeSat development, was formulated concept of the design process and established physical relationships to find some optimal design solution about compatibility of basic parameters and characteristics. In addition, considering some images of the CubeSat model, and discussing the traditional manufacturing technology and 3Dprinting technology, it finally gets two new designs of the CubeSat structure, and the best 1U CubeSat model is selected for manufacturing (Figure 10).

None.

The author declares that there is no conflict of interest.

1. Small spacecraft technology state of the art 2015 tagged. Mission Design Division, Ames Research Center, Moffett Field, California; 2015. 173 p.
2. Gao S, Unwin M, Zackrisson J, et al. Antennas for modern small satellites. IEEE Antennas and Propagation Magizine. 2009;51(4):40‒56.
3. Shiroma WA, Akagi JM, Akagi JT, et al. CubeSats: A bright future for nanosatellites. Central European Journal of Engineering. 2011;1(1):9‒15.
4. Shufan Wu, Wen Chen, Caixia Chao. The STU-2 CubeSat Mission and In-Orbit Test Results. Utah: 30th Annual AIAA/USU Conference on Small Satellites; 2016.
5. Manzoni G, Zhang M, Brama YL. Athenoxat-1, Night Vision Experiments in LEO. Logan, Utah: 30th Annual AIAA/USU Conference on Small Satellites–Cubesat workshop; 2016.
6. Kerner H. The Lunar polar Hydrogen Mapper (LunaH-Map) CubeSat Mission. Logan, Utah: 30th Annual AIAA/USU Conference on Small Satellites; 2016. 9p.
7. Ampatzoglou A, Kostopoulos V. Design, Analysis, Optimization, Manufacturing, and Testing of a 2U Cubesat. International Journal of Aerospace Engineering. 2018;9724263:1‒15.
8. Lee S, Toorian A, Lan W, et al. CubeSat design specification Rev.13. The CubeSat program, San Luis Obispo: California Polytechnic State University; 2014.
9. Zosimovych N. General Technique for Solving Structural and Parametric Optimization of Flying Vehicle Structures. Presented at the “Naukowa Przestrzeń Europy–2017. Przemyśl, Poland: XIII International Scientific and Practical Conference; 2017.
10. Rahmat-Samii Y, Kovitz JM, Manohar V. For Satellites, Think Small, Dream Big: A review of recent antenna developments for CubeSats. IEEE Antennas and Propagation Magazine. 2017;59(2):22‒30.
11. Athirah N, Ku H, Amin NAM, et al. Stress and Thermal Analysis of CubeSat Structure. Applied Mechanics and Materials. 2018;554:426‒430.
12. Zosimovych N. Functional Simulation of the Integrated Onboard System for a Commercial Launch Vehicle. Int Refer J Eng Sci. 2014;3(11):92‒106.
13. Zosimovych N, Denys Z. Simulation of the Dynamic Characteristics of Launch Vehicle Stabilization during Longitudinal Oscillations. IOSR Journal of Engineering. 2016;6(1):1‒9.
14. Woellert K, Ehrenfreund P, Ricco AJ, et al. Cubesats: Cost-effective science and technology platforms for emerging and developing nations. Advances in Space Research. 2011;47(4):663‒684.
15. Piattoni J, Candini GP, Pezzi G, et al. Plastic Cubesat: An innovative and lowcost way to perform applied space research and handson education. Acta Astronautica. 2012;81(2):419‒429.
16. Bena Mero, Kevin A Quillien, Malcolm McRobb, et al. PICASSO: A State of the Art CubeSat. Utah: 29th Annual AIAA/USU Conference on Small Satellites; 2015. 8p.
17. Zosimovych N, Chen Z. CubeSat Design and Manufacturing Technique Analysis. IOSR Journal of Engineering. 2018;8(9):1‒6.