This thesis, after a systematic and in-depth analysis of known nuclides, pro-poses a new model of nuclides’ shell structure and offers a table of the shell structures of 935 nuclides. With this theoretic approach, the thesis studies the shell combination with a bias towards the statistical analysis of nuclide structures. This thesis distinguishes between the basic models of nuclides and gives 7criteria for nu-clide binding, the maximal nucleonic number of each shell ($\Delta A_i$ ), combination of proton and neutron (p/n) and graphs of the nuclide growth. Based on magnetic moment, it also conducts a quantitative analysis of p/n on the shell. The nuclide structure has the characteristic of a shell and on every shell the combination of proton and neutron features clear regularity. Among the 263 elements from ${}_{\text{1}}{}^{\text{1}}$ H to ${}_{106}{}^{263}$ Sg the serial number of the most outside shell in structure are 7, and nuclides ${}_{\text{105}}{}^{\text{262}}$ Ha and ${}_{106}{}^{263}$ Sg are respectively even A and odd A 7 shells. It is not a coincidence but a reflection of the nuclide shell structure. The thesis uses the result of a statistical analysis to confirm the existence of “the magic Number” and reveals the fact that the magic number” is a reflection of p/n on nuclide shell, particularly on the outer shells. The statistical analysis reveals that the nuclide stability and its way of decay are dependent on the nucleonic combination on the most outside shell and the matching between full-filled and semi-full filled p/n, thus unveiling the general law governing the stability and decay of nuclides.

Keywords: nuclide shell structure; p/n (mass rate of proton and neutron), criteria of nuclide binding, graphs of nuclide growth, table of nuclide shell structure

In 1940s M.G. Mayer discovered that the number of protons and neutrons is 2, 8, 20, 28, 50, 82 and 126 and soon. These kinds of nuclides are stable in a special way. This characteristic is called “the magic number” law. The existence of “the magic number” indicates that the nuclide is characteristic of a shell structure. Afterwards, M.G. Mayer and J.H.D Jensen proposed, with the nuclide independent motion as its theoretic basis, the shell structure of nuclides and as a result explained the “magic number” law.¹ The Mayer’s shell structure model solved the magic numbers of 2, 8 and 20 first by using potential energy function of nuclear central force field in the model of harmonic oscillator potential well and square potential well. Then, with the analysis of splitting of energy levels, other magic numbers are obtained. Mayer’s shell structure is good in many ways. For an example, it successfully explains the characters of double magic-number nuclides and their near-by ones in both theory and experiment. But there are many examples showing grent differences between prediction and experiment such as electric quadruple moment of nucleon and magnetic moment of baryon odd-A nuclear. To solve the problem, A Bohr BR Mottelson and LJ Rainwater proposed the model of collective motion. However neither of the models gave specific from of the nclide shelll structure. We hold that circumstances inside and outside nuclear are entirely different. Inside it is similar to a free space while outside it has a powerful nuclear force. So there is no electronic orbiting motion and no steady-state distribution inside nuclear. Therefore, the model of nucleon shell structure is most likely an approximate description of the nuclide shell sturcture. The model we offer in this paper is different from the thought of Mayer, A Bohr et al. and it is based on classification of basic models of nuclides and on statistical analysis of nuclides.

Shell structure of a nuclear is a necessary result of direct proportion between its volume and its nucleon number. The volume V of a nuclear is

$V=\frac{4}{3}\text{π}{r}_0^{3}A$   (1)

In which radius $r_0$ ($r_0=1.21\times {10}^{-15}m$ ) is a constant obtained from experiment.² It is known that each nucleon has similar mass and identical volume. Suppose the nucleon inside the nuclear takes up an average space of a sphere with a radius of $r_0$ , the nuclide shell structure could be composed with diameter $r_0$ . Suppose the average space between shells is a sphere with diameter“$r_0$ ,”and the distance between two nearby shells is “$r_0$ ,” too, the geometric space $\Delta N_i$  of No.“i” shell is as follows, for the volume is directly proportional to nucleonic number:

$\Delta {{\rm N}}_i=\left\{\frac{4}{3}\pi {(i{r}_0)}^3-\frac{4}{3}\pi {\left[\left(i-1\right)r_0\right]}^3\right\}/\frac{4}{3}\pi r_0^3=i^3-{\left(i-1\right)}^3$   (2)

In the formula (2), if “i” is 1, 2, 3, 4, 5, 6 or 7, $\Delta {{\rm N}}_i$ must respectively be 1, 7, 19, 37, 61, 91 or 127, indicating geometric space of shell layers in terms of nuclide numbers. To make a distinction, nuclide with “k” shells is called k-shell nuclide. For instance ${}_8{}^{16}$ O₈ could be called 3-shell nuclide and its second shell has 4 nucleons.

There is nuclear force between nucleons, so they cannot be indefinitely close to each other. Except for $i=1$ , no shell can be covered with the maximal number of nucleons as given in formula (2). Nucleons do not fully occupy the geometric space of the shell either. The nuclide shell structure is shown in Figure 1. Suppose the actual maximal number of nucleons contained on I shell structure is,$\Delta A_i,\Delta A_i\le \Delta {{\rm N}}_i.\Delta A_i/\Delta {{\rm N}}_i$ represents the ratio of nucleons’ occupation of the shell space and reflects the fullness of nucleons. The proton-neutron ratio of each shell, called p/h for short indicates the nucleonic combination on each shell. Interdigitational distribution of nucleons on shells. It is found that, if even A nuclides are“ hollow” and obb A nuelides are “neutron centered” except for Hydrogen (H) nuclides, the shapes of nuclide shell structures may be obtained according of the pairing characteristics of nucleons and the quantitative relationship of magnetic moment. Through statistical analysis of nuclides, we propose the 7-shell structure of known nuclides. Statistical analysis shows:

1. There could be only one nucleon on the first shell, and it is always filled by neutron except for element H;
2. The maximal number $\Delta A_2$ of nucleon on the second shell is 4, that is $\Delta A_2$ = 4, so $\Delta A_i/\Delta N_i=0.5714$ . When the second shell is fulfilled, the p/n = 2/2;
3. On the 3^rd shell $\Delta A_3=12$, $\Delta A_3/\Delta N_3=0.6316$ . If the 3^rd shell is the most outside and full-filled, its p/n has only two combinations: p/n = 6/6 and p/n = 5/7;
4. On the 4^th shell $\Delta A_4=24$ , $\Delta A_4/\Delta N_4=0.6486$ , the p/n of the full-filled shell has only two combi-nations:12/12 and 10/14;
5. On the 5^th shell $\Delta A_5=48$ , $\Delta A_5/\Delta N_5=0.7868$ , the p/n of the full-filled shell has only two combinations: 20/28 and 18/30;
6. On the 6^th shell, $\Delta A_6=72$ , $\Delta A_6/\Delta N_6=0.7912$ , the p/n of the full-filled shell has only two combinations: 28/44 and 26/46;
7. On the 7^th shell $\Delta A_7=102$ , $\Delta A_7/\Delta N_7=0.8031$ , the p/n of the full-filled shell has only two combinations: 44/58 and 42/60.

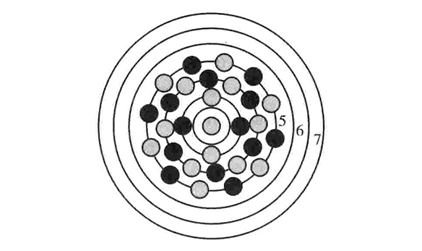
Figure 1 The Model of Nuclide Shell Structure.
In the diagram, the distance between two nearby cellsis “$r_o$ ”.Black circles stand for protons and grey ones for neutrons. Full-filled nucleon numbers of the 4^th, 5^th, 6^th and 7^th, shells are 24, 48, 72 & 102 respectively.

Except for the first and second shells, there are two kinds of stable combinations when the shell is full-filled. The first kind, represented by I, is full-proton combination and the second kind, represented by II, is full-neutron combination. The objectivity of p/n combination on each shell is a decisive factor for determine the model quality. Further quantitative analysis will be given in the following discussion of nucleonic magnetic moment.

For the maximal nucleonic numberthe shell can actually contain, the statistics of $\Delta A_1=1,\Delta A_2=4,\Delta A_3=12,\Delta A_4=24,\Delta A_5=48,\Delta A_6=72,\Delta A_7=102$  provided by us is of important significance for the statistic models of plastic shell structure. In implementation this group of statistics may be obtained from the ratio between $\Delta A_i$ and $\Delta {{\rm N}}_i$ and the natural abundance of corresponding nuclides.

The nucleonic action inside the nucleus is related to the included angle of nucleonic magnetic moment. The acting force gradually increases as the shell structure enlarges, the nuclear radius becomes longer and the magnetic moment angle becomes smaller between nuclides, making the $\Delta A_i/\Delta {{\rm N}}_i$ ratio tend to increase. Therefore, we come to the following judgment:

$\Delta A_i/\Delta N_1<\Delta A_2/\Delta N_2<\Delta A_3/\Delta N_3<\Delta A_4/\Delta N_4<\Delta A_5/\Delta N_5<\Delta A_6/\Delta N_6<\Delta A_7/\Delta N_7<\alpha$   (3)

α Being an actual number smaller than 1.

The $\Delta A_i$ may be deduced from the relationship shown in Formula (3) and the stability of corresponding nuclide. Taking even A nucleus as an example, we know that the helium (He) nucleus has stable nuclides of sphere symmetry and is often used as bullet to attack other nuclei. From this we infer that ${}_2{}^4$ He is the even A full-filled nuclide of the second shell level and $\Delta A_2=4$ , $\Delta A_2/\Delta N_2=4/7=0.571$ . For even A nuclides of the 3^rd shell level,

Because

$\Delta A_3/\Delta N_3=\Delta A_3/19>0.571$   (4)

So $\Delta A_3>10.894$ . Noticing the characteristic of even integer of even A, $\Delta A_3$ can only be chosen from among 12, 14, 16 and 18. Since $18/19\to 1$ , as a matter of fact $\Delta A_3$ can only be chosen from 12, 14 and 16. Again, because the nucleus number of full-filled nuclides of Even A of 2^nd shell level is 4, the nucleus number of full-filled nuclides of even A of 3^rd shell level can only be taken from 16, 18 and 20. Seeing that the nuclides hose nucleus numbers are 18 and 20 lack high abundance stability, the nucleus number of even A full-filled nuclides of the 3^rd shell level can be none other than 16 and the corresponding nuclide is ${}_8{}^{16}$ O₈. $\Delta A_3=12,\Delta A_3/\Delta N_3=12/19=0.6316$ .

For full-filled nuclides of even A of the 4^th shell level, because

$\Delta A_4/\Delta N_4=\Delta A_4/37>0.6316$   (5)

$\Delta A_4>23.369$ , so $\Delta A_4$ can only be chosen from among 24, 26, 28 and 30. The corresponding full-filled nucleus numbers of even A are respectively 40, 42, 44 and 46. We notice that none of the nucleus numbers 42, 44 and 46 have nuclides of high abundance stability while A=40 has two nuclides of high abundance of stability: ${}_{18}{}^{40}$ Ar₂₂ and ${}_{20}{}^{40}$ Ca₂₀, and their graduations are 99.60 and 96.94. The full-filled nuclides have good stability, and from this we can judge that the full-filled nucleus number of even A of the 4^th shell level is 40. $\Delta A_4=24,\Delta A_4/\Delta N_4=24/37=0.6486$ .

For full-filled nuclides of even A of the 5^th shell,

$\Delta A_5/\Delta N_5=\Delta A_5/61>0.6486$   (6)

$\Delta A_5>39.56$ , so $A_5$ can only be chosen from among 40, 42, 44, 46, 48 and 50. Because even A nucleus A₄=40, the full-filled nucleus numbers of even A of the 5^th shell level are respectively 80, 82, 84, 86, 88 and 90. From the analysis of the natural abundance of stable nuclides, we can infer that the full-filled nucleus number of even A of the 5^th shell level is 88, the corresponding nuclide is ${}_{38}{}^{88}$ Sr₅₀ and the abundance is 82.60. $\Delta A_5=48,\Delta A_5/\Delta N_5=48/61=0.7869$ .

For full-filled nuclides of even A of the 6^th shell level,

$\Delta A_6/\Delta N_6=\Delta A_6/91>0.7869$   (7)

$\Delta A_6>71.608$ , so $\Delta A_6$ can only be selected from among 72, 74, 76, 78 and 80 and the corresponding the full-filled nucleus numbers of even A are respectively 160, 162, 164, 166 and 168. From the ratio between $\Delta A_i$  and $\Delta {{\rm N}}_i$ , we can see that the $\Delta A_i/\Delta {{\rm N}}_i$ values of the 3^rd and 4^th shell levels are close to each other and the $\Delta A_5/\Delta N_5$ value of the 5^th shell level is clearly enlarged. Because $\Delta A_i/\Delta {{\rm N}}_i<\alpha <1$ , the $\Delta A_6/\Delta N_6$ and $\Delta A_7/\Delta N_7$ cannot possibly maintain the increase rate of $\Delta A_5/\Delta N_5$ . From the analysis of the abundance of stable nuclides, it can be determined that the full-filled nucleus number of even A of the 6^th shell level is 160 and the corresponding nuclides are respectively ${}_{64}{}^{160}$ Gd₉₆ and ${}_{66}{}^{160}$ Dy₉₄, $\Delta A_6=72$ , $\Delta A_6/\Delta N_6=72/91=0.7912$ .

Experiments reveal that the maximal nucleus number of even A nucleus is 262, which conforms to the characteristics of even A full-filled nucleus number of the 7^th shell level. Since 262 is the biggest nucleus number of even A, it must be the number of full-filled nuclei. If, $A_7=262$ , $\Delta A_7=102,\Delta A_7/\Delta N_7=102/127=0.8031$ , which fully agrees to the relationship shown in Formula 3. From this we can come to the following judgment: 262 is the full-filled nucleus number of even A of the 7^th shell level and the corresponding nuclides are respectively${}_{105}{}^{262}$ Ha₁₅₇ and ${}_{107}{}^{262}$ Bh₁₅₅.

After the full-filled nucleus number of even A is determined, that of odd A is at the same time determined. Because the even A nuclei are hollow nuclides and the odd A nuclei are neutron-star nuclides, the addition of one nucleus to even A full-filled nuclei does not alter the nucleus number at various shell levels. From this we know that the full-filled nucleus numbers of odd A are respectively $A_1=1,A_2=5,A_3=17,A_4=41,A_5=89,A_6=161and{A}_7=263$ . The corresponding nuclides are respectively ${}_1{}^1$ H₁, ${}_8{}^{17}$ O₉, ${}_{19}{}^{41}$ K₂₂, ${}_{39}{}^{89}$ Y₅₀, ${}_{66}{}^{161}$ Dy₉₅ and ${}_{106}{}^{263}$ Sg₁₅₇. Here, the nucleus numbers 41, 89 and 161 correspond to the nuclides ${}_{19}{}^{41}$ K₂₂, ${}_{39}{}^{89}$ Y₅₀ and ${}_{66}{}^{161}$ Dy₉₅. This is an important enlightenment for us to better understand the fundamental categorization of nuclides. Especially, the heaviest nuclide ${}_{106}{}^{263}$ Sg₁₅₇ of the laboratory exactly fills up the position of odd A full-filled nucleus of the 7^th shell level. It provides a convincing evidence for the fundamental classification method of nuclides.

The nucleus number $\Delta A_i$ of the shell level offers a general description of the nuclei of the level. To conduct an in-depth analysis of the shell-level structure, we have to probe into the combinations of the shell level nuclei, so as to find the specific forms combination between protons and neutrons. The proton-neutron combination ratio p_i/n_i at the shell level is determined by the pairing characteristics of nuclei and the quantitative relation of nucleus magnetic moments. A nucleus pairing is the basic condition for the formation of nuclides. The fact that nuclei have magnetic moments means that, apart from nuclear force, there also exists electromagnetic force. Experiments show that the force between nuclei is related to the included angle of the nucleus’s spin angular momentum.³

Let’s take even A nuclei as an example. He₂ is the nuclide of full-filled 2^nd shell level. The nucleus of the first shell level is vacant. The 2^nd level has 4 nuclei and the proton-neutron is p2/n2=2/2. O8 is the nuclides of the full-filled 3rd shell level. The proton-neutron ratios of the 2nd and 3rd levels are p2/n2=2/2 and p3/n3=6/6. Ca20 refers to the nuclides of the full-filled 4th shell level and the proton-neutron ratios of the 2^nd, 3^rd and 4^th levels are p2/n2=2/2, p3/n3=6/6 and p4/n4=12/12. The 3 kinds of nuclides are all highly abundant and stable. This shows that p2/n2=2/2, p3/n3=6/6 and p4/n4=12/12 are the stable combinations of proton-neutron ratios of the 2nd, 3rd and 4th shell levels. This type of combinations is characteristic of one-to-one pairing between protons and neutrons. Please refer to Figure 2 for nuclide pairing.

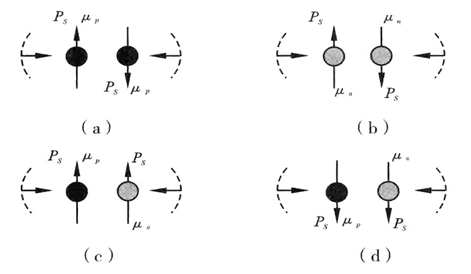
Figure 2 Pairing of Nucleons.
Nucleons of the same kind expel each other when in the same direction and attract each other when in opposite directions. Nucleons of different kinds attract each other when in the same direction and expel each other when in opposite directions.

With more shell levels and more neutrons, the nuclei of high levels no longer have conditions for one-to-one pairing between protons and neutrons. But the proton-neutron ratio (pi/ni) can be obtained by quantitative analysis of the ratio of nucleus magnetic moments. The magnetic force of nucleons is shown in Figure 3.⁴

Figure 3 Magnetic Force of Nucleons.
Magnetic moments of the same kind of nucleons attract each other when in the same direction and expel each other when in opposite directions. Those of different kinds of nucleons attract each other when in the same direction and expel each other when in opposite directions.

Experiment tests show that the proton magnetic moment ${\mu }_p=2.792847386$ (63) ${\mu }_N$ , the neutron magnetic moment ${\mu }_n=－1.91304275$  (45) ${\mu }_N$  and their relative rate is

$\left|\frac{{\mu }_p}{{\mu }_n}\right|=1.46$   (8)

This relative rate represents the strength level of the eddy field caused by proton or neutron spin. Nucleons on stable shells are in a state of balance of electromagnetic force. I.e. the eddy fields of protons and neutrons are in mutual balance. Except such nuclides as ${}_8{}^{16}$ O₈ and ${}_{20}{}^{40}$ Ca₂₀, total balance of the proton and neutron eddy fields on all shells should be maintained, Formula (8) indicates that, when the p/n of all shells approaches 1/1.46, the electromagnetic force is in balance on the whole. The nucleon number is a natural one and even-even nucleons tend to be stable. With the above characteristics in mind, we can give a semi-quantitative explanation about the combinations of p/n’s on all shells.

Statistical analysis reveals that p/n = 5/7, p/n = 10/14 and p/n = 20/28 are respectively a stable combination of the full-filled p/n of the 3^rd,4^th and 5^th shell. It is no co-incidence that the p/n rate of the 3 shells is 1/1.4. It is a manifestation of the magnetic moment of protons and neutrons and also a manifestation of the strength level of the eddy field caused by a proton or neutron spin. A stable shell is in a balance state of electromagnetic force and is full-filled with neutrons. For any shell, if the quantity of protons is $p_i$ , the quantity of neutrons $n_i\approx 1.46p_i$ . Thus, we have the following:

$p_i+n_i=p_i+1.46p_i=\Delta A_i\cdot$   (9)

In the formula $\Delta A_i$ stands for the maximal number of nucleonson “i” shell. If p_i is figured out, the nucleonic combination on “i” shell can be known.

For the 3^rd shell

$p_3+1.46p_3=12,p_3=4.88,$

After rounding it off to an integer

$p_3=5, =7, p_3/n_3=5/7.$

For the 4^th shell

$p_4+1.46p_4=24, p_4=9.76,$

After rounding it off to an integer

$p_4=10, n_4=14, p_4/n_4=10/14.$

For the 5^th shell

$p_5+1.46p_5=48, p_5=19.51,$

After rounding it off to an integer

$p_5=20, n_5=28, p_5/n_5=20/28.$

For the 6^th shell

$p_6+1.46p_6=72, p_6=29.27,$

After rounding it off to an integer

$p_6=28, n_6=44, p_6/n_6=28/44.$

For the 7^th shell

$p_7+1.46p_7=102, p_7=41.46,$

After rounding it off to an integer

$p_7=42, n_7=60, p_7/n_7=42/60.$

The calculated results are in agreement with the stable combination of protons and neutrons on full-filled shells and also with the growing graph of nuclides. If these results reflect the overall balance of nucleonic electromagnetic force on full-filled shells, the p/n ’s p₂/n₂=2/2, p₃/n₃=6/6 and p₄/n₄=12/12 reflect the single balance of the nucleonic electromagnetic force. It is a manifestation of the one-to-one pairing between protons and neutrons. And the other p/n's p₅/n₅=18/30, p₆/n₆=26/46 and p₇/n₇=44/58 are stable combination of dynamic balance of nucleonic electromagnetic force.

Although there is a con-firmed $\Delta A_i$ (maximal number of nucleons) and a stable combination of protons and neutrons on each shell, the nucleons do not remain unchanged, for they keep exchanging nucleons against the background of energy exchange with the outside world. In an instant, a quasi-full-filled shell state is formed. In general, if the combination of nucleons on the 3^rd shell in a nuclide is a full-filled one (p₃/n₃=6/6), the combination of nucleons on the 4^th shell is mostly a full-neutron one (p₄/n₄=10/14). After a pair of nucleons are exchanged, we have p₃/n₃=5/7, p₄/n₄=11/13, of which p₄/n₄=11/13 is a stable combination of inside quasi-filled shell (Figure 4 (A)).

If the nucleonic combination on the 4^th shell is a full-proton one (p₄/n₄=12/12), that on the 5^th shell is a full-neutron combination (p₅/n₅=18/30). The exchange of two pairs of nucleons results in the combination p₄/n₄=10/14, p₅/n₅=20/28, which is shown in Figure 4(B). The newly-formed combination may be restored to the original state after exchange of two pairs of nucleons. Similarly, such exchange may take place between the 5^th and 6^th shells and between the 6^th and 7^th shells. To sum up, nucleons on shells fluctuate and exchange between individual balance (e.g. p/n=6/6, p/n=12/12) and overall balance (e.g. p/n=5/7, p/n=10/14, p/n=20/28), which is controlled by the relative rate between the magnetic moment of protons and that of neutrons.

Figure 4 Exchange of Nucleons between Shells.

In the preparation of the table, no particular attention is attached to the condition of magic numbers which nevertheless do exist as a natural character of the shell structures. Let’s take ${}_2{}^4$ He₂ as an example. Its p/n=2/2 and it is a 2-shelled nuclide with full-filled structure. ${}_8{}^{16}$ O₈ is a 3-shelled nuclide with full-filled shell structure and its $\Sigma$ p/n=8/8. ${}_{20}{}^{40}$ Ca₂₀, its $\Sigma$ p/n=20/20, is a 4-shelled nuclide with fall-filled structure. ${}_{38}{}^{88}$ Sr₅₀, its $\Sigma$ p/n=38/50, is a 5-shelled nuclide with full-filled shell structure. Nuclides with full-filled structures are stable in character.

Another feature of stable nuchdes is that the p/n of most outside shell equals. Nuclides with N=20 have 5 kinds of stable nuclides of which 4 have their p/n equal one on the most outside shells. They are, ${}_{17}{}^{37}$ Cl₂₀, ${}_{18}{}^{38}$ Ar₃₀, ${}_{19}{}^{39}$ K₂₀, and ${}_{20}{}^{40}$ Ca₂₀. Their p/n’s of most outside shells are respectively 10/10, 11/11, 11/11 and 12/12. Of the 5 kinds of stable nuclides with N=28, 4 have the characteristic of p/n equaling one on the most outside shell. They are ${}_{22}{}^{50}$ Ti₂₈, ${}_{23}{}^{51}$ V₂₈, ${}_{24}{}^{52}$ Cr₂₈ and ${}_{26}{}^{54}$ Fe₂₈. Their p/n’s of the most outside shells are respectively 5/5, 5/5, 6/6 and 7/7.

There are 6 kinds of stable nuclides with N =50: ${}_{36}{}^{86}$ Kr₅₀, ${}_{37}{}^{87}$ Rb₅₀, ${}_{38}{}^{88}$ Sr₅₀, ${}_{39}{}^{89}$ Y₅₀ ${}_{40}{}^{90}$ Zr₅₀ and ${}_{42}{}^{92}$ MoY₅₀.It is known from Table 1 that, of all the p/n’s of full-filled shells on the 5^th shell have two combinations of p/n =20/28 and p/n=18/30. The p/n’s of the most outside shells of ${}_{36}{}^{86}$ Kr₅₀ and ${}_{37}{}^{87}$ Rb₅₀ are 18/28 and 18/28, close to the p/n of the 5^th shell. For ${}_{38}{}^{88}$ Sr₅₀ and ${}_{39}{}^{89}$ Y₅₀, the p/n’s are both 20/28, identical with the combinations on the 5^th full-filled shell. ${}_{40}{}^{90}$ Zr₅₀’s and ${}_{42}{}^{92}$ Mo₅₀ are 6-shelled nuclides with their p/n’s on the 6^th shell being 1/1 and 2/2.

Of the heavy nuclides with N=82, seven are stable ones: ${}_{54}{}^{136}$ Xe₈₂, ${}_{56}{}^{138}$ Ba₈₂, ${}_{57}{}^{139}$ La₈₂, ${}_{59}{}^{141}$ Pr₈₂, ${}_{60}{}^{142}$ Nd₈₂ and ${}_{62}{}^{144}$ Sm₈₂.They are all 6 shelled and their p/n’s of the most outside shells are respectively 18/30, 20/30, 20/30,22/30, 22/30, 24/30 and 24/32.

Nuclides have shell structures and stable nuclides have stable p/n’s on the most outside shells. But with the increase of nucleonic number A, the filling level of neutrons grows higher and the p/n of the most outside shells is smaller than one. For the 7 stable nuclides with N=82, the p/n valve of the most outside shells changes around 1/1.5. So it is known that this characteristic is relevant to the magnetic moment of nucleons.

Nuclides with N=126 are 7-shell structured and there are two stable nuclides: ${}_{82}{}^{208}$ Pb₁₂₆ and ${}_{83}{}^{209}$ Bi_126. Their p/n’s of the most outside shells are 18/30 and 20/28, identical with the two stable combinations of the 5^th shell when it is full-filled. This shows that a nuclide may become stable when its combination of protons and neutrons of the most outside shells in consistent with the stable nucleonic combination of an inside shell.

Heavy nuclides with $Z\ge 84$ are unstable except ${}_{90}{}^{232}$ Th_142, ${}_{92}{}^{235}$ U₁₄₃ and ${}_{92}{}^{238}$ U₁₄₆.They are 7-shell structured and their p/n’s of the most outside shells are respectively 26/46, 28/46 and 28/50. Except even-even nucleonic combination of the most outside shells, being identical with or close to the p/n’ s of the 6th shell is also a prerequisite for the nuclide stability. To sum up, it could be presumed that the stability of a nuclide is decided by p/n combination on the most outside shells and on the p/n filling level of each shell. The "magic number" is the reflection of this feature. Except the case that the numbers of protons or neutrons are 2, 8 or 20, other magic numbers reflect nucleonic number of unfull-filled shells. So magic numbers reflect the combinations of protons and neutrons of stable nuclides.

Decay modes of unstable nuclides are dependent on the nucleonic combinations of outside shells. The Table of Nuclide Shell Structure (See the appendix) indicates that a nuclide decays in the $\left(\epsilon \right)$ way when its p-n of the most outside shell is 2, 4 or 6 and it decays in the $\left({\beta }^{-}\right)$ way when its outside shell n-p is 2, 4 or 6.This characteristic remains true after nearly 1000 unstable nuclides are tested.

Unstable nuclides decaying in the $\left(\epsilon \right)$ way are characterized by the nucleonic numbers on outside shells being even numbers of 2, 4, 6, etc. Judging from the condition of forming a nuclide, we know from Figure 2 (a) that pairing of protons in the abnormal (reverse) direction caused by magnetic moment is a kind of pairing style. The magnetic moment of a proton is l.46 times more powerful than that of a pair of a neutron and the electromagnetic force of a pair of protons is l.46 times more powerful than that of a pair of neutrons. We know that the pairing of protons and neutrons is an important pre-requisite for a nuclide to form. Therefore, a pair of protons is unstable which can distribute on the most outside shell for a short time. By absorbing an electron, a proton turns into a neutron, thus forming a stable nucleonic pair. So the nuclide becomes stable and this is the cause of $\left(\epsilon \right)$ way of decay.

The unstable nuclides which decay in the $\left({\beta }^{-}\right)$ way are characterized by the even number of nucleons on the outside shells, 2, 4, 6, etc. When protons and neutrons on outside shells fail to strike individual or overall balance, superfluous neutrons pair in reverse direction caused by magnetic moment, as is shown in Figure 2(B). But the electromagnetic force between pairs of neutrons is l.46 greater than that between proton-neutron pairs. It is less powerful than the combination ability of proton-neutron pairs, so the neutron pair is also unstable and can only be distributed on outside shells. By the force of proton-neutron pairs in the neighboring field, one of the neutrons becomes a proton after discharging an electron. A stable nucleonic pair is formed and the nuclide is made stable. And this is the cause of “${\beta }^{-}$ ” way of decay. It is surprising that No. 42 element Mo and No. 44 element Ru each have 7 stable isotopes while No. 43 element Tc between them has no stable nuclides at all. The Table of Nuclide Shell Structure tells us that element Tc could not form structure with suitable p/n among the cells and its p/n of the most outside shell is not one.

The $\left(\alpha \right)$ way of decay of heavy nuclides is a reflection of the evolution of the p/n combination of most outside shells from unstable to stable. For instance, the outside shell p/n of stable nuclide ${}_{83}{}^{209}$ Bi₁₂₆ is 20/28. As for unstable nuclide ${}_{85}{}^{213}$ At₁₂₈, its outside shell p/n is 22/30 and the product after its $\left(\alpha \right)$ way of decay is ${}_{83}{}^{209}$ Bi₁₂₆, tending to be stable. Let’s cite another example, the stable nuclide ${}_{92}{}^{238}$ U₁₄₆has its outside shell p/n at 28/50. The unstable nuclide ${}_{94}{}^{242}$ Pu₁₄₈has it at 30/52, tending to be stable after its decay in the $\left(\alpha \right)$ way. Thus, the conclusion is drawn that the decay mode depends on nucleonic combination of the most outside shells. Unstable nuclides which decay in the $\left(f\right)$ way result from the imbalance of p/n’s between shells.

The heavy nuclide confirmed by experiment is ${}_{106}{}^{263}$ Sg₁₅₇. It is a neutron-filled nuclide with a 7-shelled full-filled structure. It decays by free fission. If there exists a heavier nuclide with a super-large N number, it must be 8-shell structured. It is presumed from Table 1 about the specific value ($\Delta A_i/\Delta N_i$ ) of the shell space nucleons take up that the maximal number of nucleons ΔA₈ which can be accommodated by the 8^th full-filled shell should be 136 $[(8^3-7^3)\times 0.81]$ . If the number of protons on the 8^th shell is equal to that of neutrons on the 7^th shell, it is a pre-requisite for the stable combination of p/n’s of the 8^th shell. The p/n’s of full-fdled 8^th shell are 60/76 and 58/78. From this we may calculate that the nucleonic number A of an even-A nuclide with 8 full-filled shells is 398. MG Mayer predicked the existence of Z=114 supper-heavy nuclide. At the end of last century, scientists of Joint Institute for Nuclear Research announced that they had successfully produced Z=114 nuclide, its atomic weight being 289 and its half of decay being 30 seconds which is much longer than other nearby nuclides⁵ Our theory on nuclide shell structure tells us that, if the nuclide whit Z=114 and A=287 tends to be stable, its structure should be as follows:

The mass average of a nuclear is lighter than the mass sum of free nucleons of the nuclear. The difference between the two is called mass loss. Take $\Delta m\left(Z,A\right)$ for an example,

$\Delta m\text{(}Z\text{,}A\text{)}\equiv Z{m}_p+(A-Z)m_n-m(Z,A)$ ,  (10)

In the formula, $m\left(Z,A\right)$ is the mass of the nuclide. All nuclears suffer mass loss, i.e. $\Delta m\left(Z,A\right)>0$ .

When the nuclear mass is represented by $M\left(Z,A\right)$ ,

$\Delta m\left(Z,A\right)=\Delta M\left(Z,A\right)=Z{(}^{1}H)+(A－Z)m_n－M\left(Z,A\right)$   (11)

In the formula (¹H) stands for the mass of atom hydrogen. According to the relationship between mass and energy in relativity theory, the binding energy of an atom is

$B（Z,A）\equiv \Delta m（Z,A）c^2$   (12)

The nucleonic radium calculated by the mass formula is R=1.21 (F), but it is R=0.8 (F) according to the test conducted by R. Hofstadter in his experiment on electronic scattering. This proves that in the nucleon is a rim with a thickness of t=0.4 (F).⁶

The binding energy of a nuclide increases as the nucleonic number grows larger. The binding energy difference between different nuclides is great, but no regularity is discovered. Theoretically, the average binding energy of each nuclide is used to represent the level of tightness of the binding energy. The specific binding energy is

$\epsilon （Z,A）=B（Z,A）/A$   (13)

It represents the average work done on each nucleon when the nuclear with mass number A and electric charge number Z is fragmented into free nucleons. Graph of specific binding energy obtained from experiments is shown in Figure 5.⁷

Figure 5 $\epsilon -$ A Curve (Note the change of coordinate scale after $a\ge 30$ ) ${}^{②}$ .⁸

Both theory and experiments prove that the binding energy ε value of an even-A nuclide with full-filled shells is relatively high at its peak value. This rule can be confirmed by working out the binding energy of the last nucleon. The significance of the last nucleon’s binding energy refers to the energy released when a free nucleon and other nucleons of the nuclear combine into a nuclide. In other words, it is the energy needed to separate a nucleon from the nuclear.

The binding energy of the last proton is

$S_p\left(Z,A\right)=B\left(Z,A\right)-(Z-1,A-1).$   (14)

The binding energy of the last neutron is

$S_n\left(Z,A\right)=B\left(Z,A\right)-B(Z,A-1).$   (15)

From the value surplus in $\Delta (Z,A)$  Table of Nuclide Shell Structure, the definition of $\Delta (Z,A)$ and Formula

$\Delta (Z,A)=[M\left(Z,A\right)-A]c^2,$   (16)

Can be used to work out the binding energy of a nuclide and that of the last nucleon. ${}_{\text{8}}{}^{\text{16}}$ O₈ is a 3-shelled full-filled nuclide of “$○$ ”category. From the definition of $S_p，S_n$  we can work out the following:

$\begin{array}{l}{S}_p({}_{\text{8}}{}^{16}O)=12.12MeV, S_n({}_{\text{8}}{}^{16}O)=15.66MeV\\ S_p({}_9{}^{17}F)=0.61MeV, S_n({}_{\text{8}}{}^{17}O)=4.15MeV\end{array}$

${}_{\text{20}}{}^{\text{40}}$ Ca₂₀ is a 4-shelled nuclide of “”category. $S_p,S_n$ values of neighboring nuclides are:

$\begin{array}{l}{S}_p({}_{20}{}^{40}Ca)=8.38MeV, S_n({}_{20}{}^{40}Ca) =15.68MeV\\ S_p({}_{21}{}^{42}Sc)=4.27MeV, S_n({}_{20}{}^{41}Ca)=8.32MeV\end{array}$

${}_{38}{}^{88}$ Sr₅₀ is a 5-shelled full-filled nuclide of the “$○$ ” category. $S_p,S_n$ values of neighboring nuclides are:

$\begin{array}{l}{S}_p({}_{38}{}^{88}Sr)=9.94MeV, S_n({}_{38}{}^{88}Sr)=10.45MeV\\ S_p({}_{39}{}^{89}Y)=7.74MeV, S_n({}_{39}{}^{89}S)r=7.03MeV\end{array}$

${}_{\text{64}}{}^{\text{160}}$ Gd and ${}_{\text{66}}{}^{\text{160}}$ Dy are 6-shelled full-filled nuclides of the “$○$ ”category. $S_p,S_n$ values of neighboring nuclides are:

$\begin{array}{l}{S}_p({}_{64}{}^{158}Gd)=8.51MeV, S_n({}_{\text{64}}{}^{\text{160}}Gd)=7.45MeV\\ S_p({}_{65}{}^{161}Tb)=6.81MeV, S_n({}_{\text{64}}{}^{\text{161}}Gd)=5.63MeV\end{array}$

And

$\begin{array}{l}{S}_p({}_{66}{}^{160}Dy)=7.43MeV, S_n({}_{66}{}^{160}Dy)=8.58MeV\\ S_p({}_{67}{}^{165}Ho)=6.22MeV ,S_n({}_{66}{}^{161}Dy)=6.45MeV\end{array}$

The above results show that the peak values of $S_p$  and $S_n$  appear on full-filled nuclides.

Table 2 shows the binding energy of some isotopes $S_n\left(Z,A\right)$ of nuclides with fulfilled shells. We can see that nuclides ${}_{\text{8}}{}^{16}$ O，${}_{\text{20}}{}^{\text{40}}$ Ca， ${}_{38}{}^{88}$ Sr， ${}_{39}{}^{89}$ Y and ${}_{66}{}^{160}$ Dy show their peak values of $S_n\left(Z,A\right)$ when full-filled.

Table 1 show that the ratio $\Delta A_i/\Delta N_i$  is between 0.571 and 0.803 and increases as the number of shells becomes larger, which is consistent with the fact that the distance between nearby nucleons decreases as the radius of curvature becomes larger.

The full-filled shell nuclide refers to the nuclide, each of whose shells has been filled with $\Delta A_i$ . Only after the inside shells are fully filled, will the outside ones begin to full fill. Therefore, the un full-filled shells only refer to those outside ones whose proton is smaller than $\Delta A_i$ .

The statistical analysis shows that, except for ${}_{18}{}^{40}$ Ar, in the stable nuclides of the 2^nd, 3^rd and 4^th shells, the p/n is 1 and the protons and neutrons are very likely to pair with each other. If the shells are naturally stable, the p/n of most outside shells is 1.

When the 5^th, 6^th and 7^th shells are full-filled, the p/n's of the most of their outside shells are 1, showing a big regularity. So we can make out the shell structure table of all the nuclides with the principle of the table, their pairing characteristic and the combining criteria shown in the nuclide structure. The major criteria of nuclide combination are the following 7.

1. The proton cannot occupy the first shell of a nuclide except for element H.
2. Every shell of a nuclide is filled with nucleons of even number except the first shell which is either unfilled or filled with a neutron. The nuclide with an unfilled first shell is called hollow nuclide symbolized by “$○$ ”. The nuclide with a filled first shell is called neutron-filled nuclide symbolized by “$\odot$ ”. They are two basic kinds of nuclides. The even A nuclides are “$○$ ” kind and the odd A nuclides belong to “$\odot$ ” kind.
3. For nucleons show the characteristic of pairing with each, nucleonic number of the most outside shells is even with the exception of element H. The p/n of the most outside shells of stable nuclides is most likely to be 1.
4. For any nuclides with k shells, there are only 2 kinds of combinations of p/n in full-filled shells except for the 2^nd shell, as is shown in the following:

1. 2^nd shell: p/n=2/2, and if $k>2$ , then p₂=2, n₂=2;
2. 3^rd shell: p/n=6/6, p/n=5/7; and if $k>3$ , then $p_3\le 6,n_3\le 7$ ;
3. 4^th shell: p/n=12/12, p/n=10/14; and if $k>4$ , then $p_4\le 12,n_4\le 14$ ;
4. 5^th shell: p/ =22/28, p/n=18/30; and if $k>5$ , then $p_5\le 20,n_5\le 30$ ;
5. 6^th shell: p/n=28/44, p/n=26/46; and if $k>6$ , then $p_6\le 28,n_6\le 46$ ;
6. 7^th shell: p/n=44/58, p/n=42/60; and if $k>7$ , then $p_7\le 44,n_7\le 60$ .

5. If the p/n of the most outside shell is not 1, generally $\left|p-n\right|$ =2. For the nuclide of $\left|p-n\right|\ne 2$ , the p/n is an even number.
6. The mode of nuclide decay depends on the nucleonic combination of its most outside shell.
7. The stability of a nuclide depends on the p/n relationship between shells. Generally, the filling level of the p/n of each shell of a stable nuclide is invariably I, but its shells are full-filled or unfull-filled alternatively in the II kind of nuclides.

To determine values of $\Delta A_i$ and the p/n combinations is the principal basis for the preparation of the nuclide shell structure table. The regularity shown in $\Delta A_i$ and p/n is embedded in the graph of nuclide growth. The developing route of full-filled nuclides is shown in Figure 6(A) & Figure (B). Figure 6(A) is the route of the development of even A full-flied nuclides and Figure 6(B) is that of odd A full-filled nuclides. The 1^st, 2^nd, 3^rd and 4^th shells are the same as the shell structure proposed by Mayer, but the 5^th, 6^th and 7^th shells are obviously different in the number of nucleons.⁸

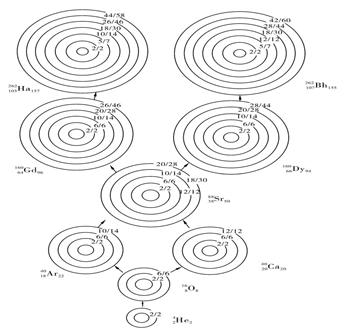
Figure 6A Developing Route of Even A nuclides.
Even A nuclide belongs to “⊙” category and its first shell is vacant. With the second shell full-filled, its stable nuclide is ${}_2{}^4$ He₂; with the third shell full-filled, its stable nuclide is ${}_8{}^{16}$ O₈; with the fourth shell full-filled, its stable nuclides are ${}_{18}{}^{40}$ Ar₂₂ and ${}_{30}{}^{40}$ Ca₂₀; with tile fifth shell full -filled, its stable nuclide is ${}_{38}{}^{88}$ Sr₅₀; with the sixth shell full-filled, its stable nuclides are ${}_{64}{}^{160}$ Gd₉₆ and ${}_{64}{}^{160}$ Dy₉₄; with the seventh shell full- filled, its stable nuclides are ${}_{105}{}^{262}$ Ha₁₅₇ and ${}_{107}{}^{262}$ Bh₁₅₅, ${}_{105}{}^{262}$ Ha₁₅₇ and ${}_{107}{}^{262}$ Bh₁₅₅ are exactly the nuclides of the seventh shell. This figure derives from Table 1.

Figure 6B Developing Route of Odd A nuclides.
Odd A nuclide belongs to “⊙” category. Except for Element H, the first shell is invariably filled with neutrons. With the second shell full- filled, its nuclide ${}_2{}^5$ He₃ is unstable; with the third shell full- filled, it is the isotope ${}_8{}^{17}$ O₉ of the lowly full-filled O; with the fourth shell full-filled, the nuclides include stable nuclide ${}_{19}{}^{41}$ K₂₂ and unstable nuclide ${}_{20}{}^{41}$ Ca₂; with the fifth shell full -filled, the nuclide is ${}_{39}{}^{89}$ Y₅₀ stable; with the sixth shell full- filled, the nuclide ${}_{66}{}^{161}$ Dy₉₅ is stable. ${}_{106}{}^{263}$ Sg₁₅₇ is exactly the odd A nuclide of the full-filled seventh shell, The figure derives from Table 1.

Any nuclide is first of all categorized according to the nature of nucleon A, i.e. whether it is odd or even in number, and then it is filled with nucleons one shell after another from inside to outside. The p/n of each shell is determined by the afore-mentioned 7 criteria. For an example, ${}_{17}{}^{35}$ Cl₁₈ is an odd A nuclide belonging to “$\odot$ ” kind. So its first shell is filled with one neutron and its p/n's on the 2^nd, 3^rd, 4^th and the most outside shells are respectively 2/2, 6/6, 9/9 and 1. It is therefore identified as a stable nuclide.

The second example is ${}_{28}{}^{60}$ Ni₃₂. It is an even A nuclide belonging to “$○$ ” kind. Its first shell is not filled. Its p/n's of the 2^nd, 3^rd, 4^th, 5^th shells are respectively and 6^th shells are respectively 2/2, 6/6, 10/14. It is a stable nuclide because p/n on the most outside shell is 1.The third example is the even A nuclide ${}_{90}{}^{232}$ Th₁₄₂ belonging to “$○$ ” kind. Its first shell is not filled. Its p/n's of the 2^nd, 3^rd, 4^th, 5^th and 6^th shells are respectively 2/2, 6/6, 10/14, 20/28 and 26/46. The 7^th shell is not full-filled, but its p/n (26/46) is the same as that of the 6^th shell. So it is presumed to be stable.

Nuclide shell structures may either be directly indicated or shown in a table. For instance, the shell structures of ${}_8{}^{17}$ O₉, ${}_{38}{}^{88}$ Sr₅₀ and ${}_{92}{}^{238}$ U₁₄₆ are illustrated as follows:

Shell structures of stable nuclides are illustrated in Table II which is prepared in accordance with the afore-mentioned criteria. All tile stable nuclides are included and special nuclides are marked with an asterisk “$*$ ” The clear regularity shown in the shell structures of stable nuclides is the basis for the preparation of this table.⁹

The Table of Nuclide Shell Structure is completed on the basis of The Table of Shell Structures of Stable Nuclide, giving consideration to the stability and decay modes of nuclides and even to the above-mentioned 7 criteria. Consideration should be given to matching between full-level and unfull level of p/n’s between shells and to decay modes of unstable nuclides in the combination of nucleons on the most outside shells. The Table of Nuclide Shell Structures prepared in this way can very well explain and predict the stability of nuclides and the decay patterns of unstable nuclides. Please refer to the appendix for the shell structures, with special nuclides marked with asterisks. Tables of Shell Structure of Stable Nuclides are included in Appendix One. Tables of Shell Structure of Nuclides are included in Appendix Two.

We’ve arrived at the following conclusions after statistics and analysis of nuclides. The known highest position of nuclides is a structure of 7 shell levels and the structure is composed with the nucleus ratios $r0$ as its unit. Nuclides are categorized into two: odd and even nuclides. Except for hydrogen nuclides, even A are hollow and odd A are neutron-star type. The statistic model based on the fundamental categorization of nuclides and the tables of shell structure of nuclides prepared on the basis of the model reveal the general law governing the stability and decay of nuclides. This law is both the effect and a proof of the fundamental categorization method of nuclides.

None.

Author declares there is no conflict of interest.

1. Kezun X, Hongfang C, Zifang Z. Modern Physics. Higher Education Press, Beijing, China. 1993.
2. Sida X. Nuclear Physics. Qinghua University Press, Beijing, China, 1992. p. 35–55.
3. Sida X. Nuclear Physics. Qinghua University Press, Beijing, China, 1992. p. 256–263.
4. Dayou C. On Origin and Characteristics of Electromagnet. Xi’an: Northwest University Press, China, 2008. p. 155–159.
5. Adams S. For the introduction of the experiment, refer to “Physics of 20th”. Translated by Fuxin Z， Zhihua X & Zhenguo X, Shanghai Science and Technology Press, China, 2006. 121 p.
6. Hofstadter R. Conducted the experiment on electronic scattering of high energy and discovered that the average radius of charged particles is 0.8 (F) and the rim thickness is t≈0.4 (F). History and Status Quo of the Atomic Theory, Beijing University press, Beijing, China, 1960. 220 p.
7. Evans RD. The Atomic Nucleus. Tata McGraw Hill Publishing Company Limited, India. 1995.
8. Krane KS. Introductory Naclear Physics. John Wiley & Sons, New York, USA, 1987. p. 1–858.
9. The fundamental data of the table come from: Nuclear Physics, P390~P405, Xu Side, published in 1992 by Qinghua university Press, China. 1992.