The first principles of thermodynamics under relativistic conditions and with allowance for surface tension were formulated. Two cases were studied - for Minkowski and Euclidean spaces. With the help of these laws, the temperature of the system was shown to vary according to Ott H at the adiabatic and non-adiabatic acceleration, i.e., the temperature increases for an observer in the laboratory reference frame as the velocity of the object increases. A Einstein considered that the temperature had, on the contrary, to decrease under these conditions as the velocity increased. It was shown where he had made an error.

Keywords: special relativity, relativistic thermodynamics, surface tension, temperature

Relativistic thermodynamics was created more than century ago-in 1907 when von Mosengeil’s article was published.¹ He was Planck’s disciple. According to von Mosengeil and Planck’s conclusions, the temperature T of the system under study has to vary proportionally to $\sqrt{1-{\beta }^2}$ under relativistic conditions and at an adiabatic acceleration $\beta =v/c$ ; v is the velocity of the system in the reference frame at rest; c is the speed of light. Einstein came to a similar conclusion.²

While studying the first principle of thermodynamics under relativistic conditions, nobody in the 20^th century took into consideration a surface tension; meanwhile this thermodynamic parameter is as important as the pressure p. Both Planck with his disciple and Einstein wrote down the first principle of thermodynamics under relativistic conditions neglecting the surface tension as well. Besides, both of the great scientists made an error integrating Gibbs’ equation; we shall show it below, in section 2.

Veitsman EV^3–5 was the first researcher who understood an importance of the surface tension for relativistic thermodynamics. He showed that the surface tension is a Lorentz invariant,³ at any rate up to a velocity. He also showed that the interface equations of state were correct under relativistic conditions providing the temperature of system under study varied in inverse proportion to $\sqrt{1-{\beta }^2}$ .⁴ Veitsman⁵ also obtained expressions for specific thermodynamic functions (J·cm^-2) under relativistic conditions (the internal energy U, the enthalpy H, the free energy F, and free enthalpy G). These functions are correct if $T~1/\sqrt{1-{\beta }^2}.$  Thus, the results obtained by Veitsman are in a full accordance with the result obtained by Ott⁶ for the relativistic temperature T , i.e., $T=T_0/\sqrt{1-{\beta }^2}$  ; (here and below the symbol "0" denotes that this quantity is at rest). All above results are completely correct for an adiabatic acceleration of the system.

Callen & Horwitz⁷ consider that the temperature T, in general, is a relativistic invariant. Finally, Eckart⁸ comes to a conclusion that temperature $\theta =const{\theta }_0$ . We will show below in section 3, that this assumption is incorrect.

M .Planck writes down the first principle of thermodynamics

$dU=dQ+dA$ ,  (1)

As

$d{U}_0=d{Q}_0-p_{0}d{V}_0$ ,  (2)

Where Q is the heat supplied to the system or removed from it (J); A the work done by the system or with it (J).

Under relativistic conditions the work A is written down by M. Planck as

$dA=-pdV+v·dG$ ,  (3)

$G=v\frac{U_0+p_0{V}_0}{c^2\sqrt{1-{\beta }^2}}$ ,  (4)

Where V is the vector of the system velocity; the momentum, the symbol “·” means vector multiplication.¹

G and

$\frac{i}{c}\left(U+pV\right)$ ,  (5)

Form the four-dimensional vector (4-vector) of energy-momentum, which has an invariant length equal to

$\frac{i}{c}\left(U_0+p_0{V}_0\right)$ ,  (6)

i is the imaginary unit.

Evidently, we can write down the first principle of thermodynamics in view of the surface tension (normal case) as

$d{U}_0=d{Q}_0-p_{0}d{V}_0+{\sigma }_{0}d{\omega }_0$ ,  (7)

Where ${\omega }_0$ is the element of area (cm²).

Then the relations (3) and (4) are written down as

$dA=-pdV+\sigma d\omega +v·dG$ ,  (8)

$G=v\frac{U_0+p_0{V}_0-{\sigma }_0{\omega }_0}{c^2\sqrt{1-{\beta }^2}}$ .  (9)

Consequently, the relations (5) and (6) should have the form

$\frac{i}{c}\left(U+pV-\sigma \omega \right)$ ,  (10)

$\frac{i}{c}\left(U_0+p_0{V}_0-{\sigma }_0{\omega }_0\right)$ .  (11)

Here we have to note that the quantity ω will transform as $v\to c$  in different ways: depending on the orientation of the surface in space^3,9 and Figures 1 & 2. Attempting to obtain the transformation law of the temperature as $v\to c$ , M.Planck used dependences (3) and (4) but not (10) and (11). Other researchers did the same taking no account of a surface tension, therefore the results obtained by them were incorrect. Thus, the main goals of this paper are:

1. Obtaining the first principle of thermodynamics under relativistic conditions in 3-D and 4-D versions taking into consideration the surface tension.
2. Obtaining the temperature transformation under these conditions from the above mentioned principle at the adiabatic and non-adiabatic acceleration.

Write down the first principle of thermodynamics (normal conditions; Euclidean case) in view of the surface tension as

$dQ=dU+d{E}_{kin}+p_{0}dV-\sigma d\omega -d{A}_{ac}- v·dG$   (12)

Where $E_{kin}$  is the macro kinetic energy of the object under study; $A_{ac}$  the work done against the system acceleration up to a velocity $v<<c$ ; $E_{kin}=A_{ac}$ . The momentum G is taken here according to (9).

We will adiabatically accelerate the object up to a relativistic velocity v now and will integrate (12) term by term from state 1 of the system to state 2 for the case represented in Figure 1 taking into account (8), (9) and the equalities $p=p_0,\sigma ={\sigma }_0,\omega ={\omega }_0$ ; it also should be noted that here and below we study not a whole object but only its part (a subsystem):

${\displaystyle \underset{1}{\overset{2}{\int }}dQ}={\displaystyle \underset{1}{\overset{2}{\int }}dU}+p_0{\displaystyle \underset{1}{\overset{2}{\int }}dV-{\sigma }_0}{\displaystyle \underset{1}{\overset{2}{\int }}d\omega }-{\displaystyle \underset{1}{\overset{2}{\int }}vdG},$   (13)

$Q_2(v)-Q_{(0)1}=U_2-U_{(0)1}+p_0{V}_2-p_0{V}_{(0)1}-{\displaystyle \underset{1}{\overset{2}{\int }}v\frac{dv}{c^2\sqrt{{\left(1-\frac{v^2}{c^2}\right)}^3}}\left\{U_0+p_0{V}_0-{\sigma }_0{\omega }_0\right\}}$ .  (14)

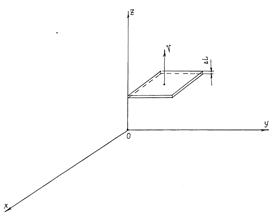
Figure 1 The moving flat interface; the velocity v of its motion is perpendicular to the flat one. ΔL is the thickness of the surface.

Now we take the integral in (14).

$\begin{array}{l}{\displaystyle \underset{1}{\overset{2}{\int }}v\frac{dv}{c^2\sqrt{{\left(1-\frac{v^2}{c^2}\right)}^3}}\left\{U_0+p_0{V}_0-{\sigma }_0{\omega }_0\right\}=\left\{U_0+p_0{V}_0-{\sigma }_0{\omega }_9\right\}{\displaystyle \underset{1}{\overset{2}{\int }}\beta \frac{d\beta }{\sqrt{{(1-{\beta }^2)}^3}}}}=\\ =\left\{U_0+p_0{V}_0-{\sigma }_0{\omega }_0\right\}{\frac{1}{\sqrt{1-{\beta }^2}}|}_1^2=\left\{U_0+p_0{V}_0-{\sigma }_0{\omega }_0\right\}\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right),\beta =v/c.\end{array}$   (15)

According to M. Planck,⁸

$U=\frac{1}{\sqrt{1-{\beta }^2}}\{U_0+{\beta }^2{p}_0{V}_0\},$   (16)

In view of the surface tension we have:

$U=\frac{U_0+{\beta }^2{p}_0{V}_0+{\sigma }_0{\omega }_0\left(\sqrt{1-{\beta }^2}-1\right)}{\sqrt{1-{\beta }^2}}$ .  (17)

Then taking into consideration (16), we can write down (14) as

$\begin{array}{l}{Q}_2(v)-Q_{(0)1}=\frac{1}{\sqrt{1-{\beta }^2}}\left\{U_0+{\beta }^2{p}_0{V}_0+{\sigma }_0{\omega }_0(\sqrt{1-{\beta }^2}-1)\right\}-U_0+p_0{V}_0\sqrt{1-{\beta }^2}-\\ -p_0{V}_0-\left\{U_0+p_0{V}_0-{\sigma }_0{\omega }_0\right\}\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right)\end{array}$ .  (18)

If we do not input the heat in an accelerated system from its source, then the left side of (18) equals zero, and we cannot obtain any dependences of the kind $T=T\left(v\right)$ ; at first sight the dependence (18) does not contain the temperature. However, this relationship contains it-in a latent form. Show it. Let an object be, e.g., the liquid moving with a relativistic velocity v. For the observer being at rest in a laboratory reference frame the temperature of this liquid depends on the cooperative velocity v of the microparticles in the object relative to its centre of mass. Then the velocity components of the total velocity w of a certain microparticle in the moving liquid equal:¹⁰

$w_1 =\frac{w_1^{\text{'}}+v}{1+\frac{v{w}_1^{\text{'}}}{c^2}}$ ,  (19a)

$w_2{}_{ }=\frac{w_2^{\text{'}}\sqrt{1-{\beta }^2}}{1+\frac{v{w}_1^{\text{'}}}{c^2}}$ ,  (19b)

$w_3=\frac{w_3^{\text{'}}\sqrt{1-{\beta }^2}}{1+\frac{v{w}_1^{\text{'}}}{c^2}}$ ,  (19c)

Where $w_i^{\text{'}}\left(i=1,2,3\right)$  are the velocity components of the microparticle in the moving reference frame.

Taking into consideration the dependences (19), it is easy to understand that the heat in the moving system increases as $v\to c$ , since the cooperative velocity of the microparticles increases in the system moving relative to its mass centre. If the heat increases, so does the temperature. However, $S=S_0$ in our case, this means $dQ=SdT$ , and (18) takes the form

$\begin{array}{l}{Q}_2(v)-Q_{(0)1}={\displaystyle \underset{1}{\overset{2}{\int }}SdT=}\left\{U_0+p_0{V}_0-{\sigma }_0{\omega }_0\right\}\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right)=\\ =\frac{1}{\sqrt{1-{\beta }^2}}\left\{U_0+{\beta }^2{p}_0{V}_0+{\sigma }_0{\omega }_0\left(\sqrt{1-{\beta }^2}-1\right)\right\}-U_0+p_0{V}_0\sqrt{1-{\beta }^2}-p_0{V}_0\end{array}$ ,  (20)

i.e., the integral in (20) gives an increment of enthalpy at the adiabatic acceleration of the system from velocity v=0 up to a velocity v for the observer being in the laboratory reference frame.

Equation (20) is completely consistent; it is correct in the range of velocities 0-v for $Q_2\left(v\right)=\frac{Q_0}{\sqrt{1-{\beta }^2}}$ . As a result, $T=T_0/\sqrt{1-{\beta }^2}$ , in accordance to Ott.⁶ If it were $Q_2\left(v\right)=Q_0\sqrt{1-{\beta }^2}$ , we would сome to absurdity as $v\to c$ . Indeed, the left side of (20) vanishes but the right side of (20) tends to $\infty .$

M.Planck as well as A. Einstein, were mistaken considering that the temperature had to transform, at adiabatic acceleration, according to the law

$T=T_0\sqrt{1-{\beta }^2},$   (21)

As $v\to \infty$ . The reason of this mistake will be shown below, in Discussion. Now we study the second case (Figure 2).

Figure 2 The moving flat interface; the velocity v of its motion is parallel to the flat one. ΔL is the thickness of the surface.

The relation (14) should now be written down in view of the relation

$\omega ={\omega }_0\sqrt{1-{\beta }^2}$ ,  (22)

As

${\displaystyle \underset{1}{\overset{2}{\int }}dQ=U_2-U_{(0)1}}+p_0{V}_2-p_0{V}_{(0)1}-{\sigma }_0{\omega }_2+{\sigma }_0{\omega }_{(0)1}-{\displaystyle \underset{1}{\overset{2}{\int }}v\frac{dv}{c^2\sqrt{{\left(1-\frac{v^2}{c^2}\right)}^3}}\left\{U_0+p_0{V}_0-{\sigma }_0{\omega }_0\right\}}$ .  (23)

Since instead of the ratio (17), we have now

$U=\frac{U_0+{\beta }^2(p_0{V}_0-{\sigma }_0{\omega }_0)}{\sqrt{1-{\beta }^2}}$ ,  (24)

Then formula (18) takes the form:

$\begin{array}{l}{Q}_2(v)-Q_{(0)1}=\left\{U_0+p_0{V}_0-{\sigma }_0{\omega }_0\right\}\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right)=\\ \frac{1}{\sqrt{1-{\beta }^2}}\left\{U_0+{\beta }^2(p_0{V}_0-{\sigma }_0{\omega }_0)\right\}-U_0+p_0{V}_0\sqrt{1-{\beta }^2}-\\ -p_0{V}_0-{\sigma }_0{\omega }_0\sqrt{1-{\beta }^2}+{\sigma }_0{\omega }_0\end{array}$ .  (25)

Taking into consideration (20), we have now:

$Q_2(v)=\frac{1}{\sqrt{1-{\beta }^2}}\left\{U_0+{\beta }^2(p_0{V}_0-{\sigma }_0{\omega }_0)\right\}+p_0{V}_0\sqrt{1-{\beta }^2}-{\sigma }_0{\omega }_0\sqrt{1-{\beta }^2}$ .  (26)

Equation (26) is correct, as and in case 1, $Q_2\left(v\right)=\frac{Q_0}{\sqrt{1-{\beta }^2}}$ if; it is incorrect if $Q_2\left(v\right)=Q_0\sqrt{1-{\beta }^2}$ .

There are more complicated cases than those represented in Figures 1 & 2, in particular, the cases of droplet or bubble, however, we do not study them in this paper.

It should be added that we come to the absurdity considering the temperature T to be a Lorentz-invariant. Now determine, how the temperature and heat have to transform under relativistic conditions when the heat is input into the system from the outside. To solve this problem, we should take into consideration that the thermodynamical state of the system is independent of the way of its transition to it. Let there be two states of the system (1 and 2) and two its intermediate ones (1' and 2'). In state 1 the system is at rest and contains some quantity of heat, which is equal to $Q_{01}$ . We input into the system an additional quantity of the heat $\Delta Q_{01}$ ; now the system is in state 1'. The heat in the system equals $Q_{01}+\Delta Q_{01}.$  Accelerate adiabatic the system up to velocity v. Now the system is in state 2; the heat of the system is

$Q_2=\frac{Q_{01}+\Delta Q_{01}}{\sqrt{1-{\beta }^2}}$ .  (27)

However, the system can go to state 2 otherwise: through state 2'. To do that, we must accelerate adiabatically the system being in state 1 up to the velocity v. Then the system will be in state 2'. Its heat equals

$Q_{2^{\text{'}}}=\frac{Q_{01}}{\sqrt{1-{\beta }^2}}$ .  (28)

Further, we input a quantity of heat into the system $\Delta Q_{2^{\text{'}}}$ and transfer it to state 2. Then the quantity of heat in the system $Q_2^{\text{'}}$ equals

$Q_2=Q_{2^{\text{'}}}+\Delta Q_{2^{\text{'}}}=\frac{Q_{01}}{\sqrt{1-{\beta }^2}}+\Delta Q_{2^{\text{'}}}$ .  (29)

Evidently,

$\frac{Q_{01}+\Delta Q_1}{\sqrt{1-{\beta }^2}}=\frac{Q_{01}}{\sqrt{1-{\beta }^2}}+\Delta Q_{2^{\text{'}}}$ ,  (30)

From equations (30) it follows that

$\frac{\Delta Q_{01}}{\sqrt{1-{\beta }^2}}=\Delta Q_{2^{\text{'}}}$ ,  (31)

Now we can formulate the first principle of thermodynamics under relativistic conditions (3-D formalism):

$dE=d{Q}_s+d{Q}_T+d{A}_d+v\cdot dG$ ,  (32)

Where $E\left(=U+E_{kin}\right)$  is the energy of the system, $Q_s$  the heat changing the entropy of the system (entropic heat). i.e., $dQ=TdS$ ; $Q_T$  the heat not changing the entropy of the system (relativistic heat) for the observer being at rest in the reference frame, i.e., $dQ=SdT=v\cdot d{G}_s$ ; $A_d$  the work of deformation, e.g., $d{A}_d=-pdV+\sigma d\omega$ .

$v\cdot d{G}_s$  the increment of the work expended on the increasing of microparticles; velocity of the system moving (the microparticles) relative to its mass centre; $v\cdot dG$ the increment of the work expended on the increasing of the system velocity from zero up to .

If $v=0$ , the law (32) will be transformed in the law (1).

Taking into consideration the relations (9) - (11), we can write down:

$G_s=\{\frac{\left(U_0+p_0{V}_0-{\sigma }_0{\omega }_0\right)}{c^2\sqrt{1-{\beta }^2}}v;\frac{i\left(U+pV-\sigma \omega \right)}{c}\}$   (33)

The quantities in braces of (33) form, in Minkowski space, a vector of energy-momentum having invariant lengths equal to

$\frac{i\left(U_0+p_0{V}_0-{\sigma }_0{\omega }_0\right)}{c},$   (34)

MØller¹¹ represents a quantity $\Delta Q_s$  as

$\Delta Q=\{G^{(h)},\frac{i}{c}\Delta Q\}$ ,  (35)

Where $\Delta G^{\left(h\right)}=\frac{\Delta Q}{c^2}v$ ; $\Delta Q$ is the amount of the heat transferred to the system during the process; in fact. $\Delta Q$ = $d{Q}_s$  (see above the law (32)).

The relation (35) was obtained by MØller¹¹ with taking into account the influence of the vessel walls, containing our substance, i.e., for a system consisting of two subsystems: substance and the vessel with its walls. It is important to note that the law (32) was obtained without accounting for the influence of the walls of the vessel.

The law (32) is correct in Euclidean space up to the velocity of system motion $v_{\max }$ . If $v>v_{\max }$ , the micro particle velocities begin to prevail in the direction X₁ over those in the directions X₂ and X₃ for the observer in the laboratory reference frame, in accordance to the relativistic law of the velocity composition. Now both the heat and temperature are not already scalars they are vectors. Then we can write down the law (32) as

$dE=d{Q}_{k(s)}k+d{Q}_{k(T)}k+d{A}_d+v·dG$ ,  (36)

Where

$k=\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)$ ,  (37)

Is the dimensionless vector; $Q_{k(s)}$ and $Q_{k(T)}$ are the vectors; $k=1,2,3$ .

Solve now the problem for 4-D case, to obtain the first principle of thermodynamics in Minkowski space. First of all, it should be noted that there were attempts to solve the problem for 4-D case, e.g.., by Eckart.,⁸ he wrote the first principle of thermodynamics as

$mD\epsilon +(1/c)[(\partial q^{\alpha }/\partial x^{\alpha }+q^{\alpha }D{u}_{\alpha })]+w^{\alpha \beta }(\partial u_{\beta }/\partial x^{\alpha })=0$ ,  (38)

$m={(-g_{\alpha \beta }{m}^{\alpha }{m}^{\beta })}^{1/2},$   (39)

Where $g{}_{\alpha \beta }$  is the fundamental tensor; $m^{\alpha }(m^{\beta })$ a four-vector which has the units g∙cm^-3, and depends only on the molecular weight and the motion of molecules; $u^{\alpha }=m^{\alpha }/m$ ; D the unique differential operator corresponding closely to the classical operator D/Dt; $\epsilon$  the internal energy (J∙kg^-1; erg∙g^-1); $q^{\alpha }$ heat flow

(J∙cm^-2 ∙s^-1); $w^{\alpha \beta }$ the stress tensor (N∙cm^-2; J∙cm^-3).

In fact, the relation (38) is an attempt to obtain the first principle of thermodynamics in a differential 4D-form. It should be noted that the term $(1/c)q^{\alpha }D{u}_{\alpha }$  does not appear in the classical case. This term is very small in all ordinary cases, and may be interpreted as a work done by a heat flow through accelerated matter, in the direction opposite to the acceleration. It may be explained as due to the inertia of energy.

The expression (38) is incorrect. The different terms in it have different units. If the relation (38) is written down as

$mD\epsilon +c[\partial q^{\alpha }/\partial x^{\alpha }+w^{\alpha \beta }(\partial u_{\beta }/\partial x^{\alpha })]+(1/c)q^{\alpha }D{u}_{\alpha }=0$ ,  (40)

Then all terms will have the same units. They have to transform identically under relativistic conditions, and we do not come to absurdity.

We have to obtain the first principle of thermodynamics in Minkowski space under relativistic conditions having taken relation (32) as a basis. To solve the problem, each term on the right side of (32) should be represented in a 4D-form. Having done it, we automatically represent, in turn, the term on the left side of (32), i.e., internal energy as 4-D physical object. Such representation of internal energy follows from the principle of two observers we formulated.

Begin the representation with the work of acceleration, i.e., $v·dG$ .

In our case the velocity components $v_{2(3)}=0$ . Then we have for components 1 and 4:

$u_{1}d{p}_1=\frac{v_1}{\sqrt{1-{\beta }^2}}d\frac{m_0{v}_1}{\sqrt{1-{\beta }^2}},$   (41)

And after the subsequent integration we have

$I_1={{С}_1\frac{m_0{v}_1^2}{2\left(1-{\beta }^2\right)}|}_0^{v_1}={С}_1\frac{m_0{v}_1^2}{2\left(1-{\beta }^2\right)}$ ,  (42)

Where $C_1$ is the normalization coefficient; u₁ the component of the 4-velocity of our object in the direction X₁.

The essence of this coefficient presented as follows. There are some of thermodynamical parameters in Relativistic Thermodynamics that equally transform in Euclidean and Minkowski spaces, e.g., the interval of time Δt or element of length Δl which is parallel to X₁. According to the energy conservation law, the energy has to vary in Euclidean and Minkowski spaces equelly, i.e., in inverse proportion to $\sqrt{1-{\beta }^2}.$

We can find this coefficient from a condition: when the velocity of the system equals v₁, then its kinetic energy $I_1=\frac{m_0{v}_1^2}{2\sqrt{1-{\beta }^2}}$ . In this case $C_1=\sqrt{1-{\beta }^2}.$  For $v<<c$ we obtain the well-known expression for the kinetic energy of a moving body for this case: $I_1=\frac{m_0{v}_1^2}{2}$ .

For the component 4 (0) we have:

$u_{4}d{p}_4=\frac{c}{\sqrt{1-{\beta }^2}}d\frac{m_{0}c}{\sqrt{1-{\beta }^2}},$   (43)

And after the subsequent integration we have, in turn:

$I_4=C_2{\frac{m_0{c}^2}{2\left(1-{\beta }^2\right)}|}_1^2=C_2[\frac{m_0{c}^2}{2\left(1-{\beta }^2\right)}-\frac{m_0{c}^2}{2}]=\frac{C_2{m}_0{c}^2}{2}\left[\frac{1}{1-{\beta }^2}-1\right],$   (44)

If the initial state is the state at $\beta =0$ . C₂ is the normalization constant for this case. It can be found from the condition: $I_4=\frac{m_0{c}^2}{\sqrt{1-{\beta }^2}}$  if the velocity of our system equals v₁. Then $C_2=\frac{2\sqrt{1-{\beta }^2}}{{\beta }^2}.$  At v=0 $I_4=m_0{c}^2,$  i.e., we have the well known ratio.

We can also represent components 1 and 4 using other representation of them in Minkowski space:

$u_{1}d{G}_1=C_1\frac{u_{(0)1}-i\beta u_{(0)4}}{\sqrt{1-{\beta }^2}}d\frac{m_0\left(u_{(0)1}-i\beta u_{(0)4}\right)}{\sqrt{1-{\beta }^2}}$ ,  (45)

$I_1=C_1{\frac{m_0\left(u_{\left(0\right)1}-i\beta u_{\left(0\right)4}\right)}{2\left(1-{\beta }^2\right)}|}_1^2$ ,  (46)

$u_{4}d{G}_4=C_2\frac{u_{(0)4}+i\beta u_{(0)1}}{\sqrt{1-{\beta }^2}}d\frac{m_0\left(u_{(0)4}+i\beta u_{(0)1\_}\right)}{\sqrt{1-{\beta }^2}},$   (47)

$I_4=C_2{\frac{m_0{\left(u_{\left(0\right)4}+i\beta u_{\left(0\right)1}\right)}^2}{2\left(1-{\beta }^2\right)}|}_1^2,$   (48)

Where $\beta =v/c.$

Now write down the expression for the work done by the pressure when the component $v_1$  of the velocity v much exceeds the components $v_{2(3)}$ , and we cannot already consider that the pressure is a relativistic invariant.

In case $v<<c$ , the increment of the work dW is written down in the real space as

$\begin{array}{l}d{W}_0=pd{V}_0\\ \Delta V_0=\Delta x_{(0)1}\Delta x_{(0)2}\Delta x_{(0)3}.\end{array}$   (49)

For the relativistic case we have, in turn:

$dW=p_{ij}Vd{\epsilon }_{ij};i,j=1,2,3,4,$   (50)

Where $p_{ij}$ is the tensor of pressure, ${\epsilon }_{ij}$  the tensor of deformation (%).

$\Delta V=\Delta x_1\Delta x_2\Delta x_3\Delta t=\Delta x_{(0)1}\sqrt{1-{\beta }^2}\Delta x_{(0)2}\Delta x_{(0)3}\frac{\Delta t_0}{\sqrt{1-{\beta }^2}}=\Delta V_0,$   (51)

Where $\Delta t_0$  is a fixed time interval which is the element of a 4D-hypercube.

Now taking into consideration (49)-(51), we will represent all terms included in the expression of the work connected with pressure.

$p_{44}d{V}_{44}={\mu }_{44}{V}_{0}d{\epsilon }_{44};{\mu }_{44}=\frac{\delta m_{44}}{\delta V_{(0)44}}=\frac{\delta \left(\frac{m_{(0)44}{с}^2}{\sqrt{1-{\beta }^2}}\right)}{\delta V_{(0)44}}$ ,  (52)

$\frac{\delta m_{(0)44}{c}^2{(\sqrt{1-{\beta }^2})}^{-1}}{\delta V_{(0)44}}d{V}_{(0)44}=d\frac{m_{(0)44}{c}^2}{\sqrt{1-{\beta }^2}}=d{{\rm Z}}_{44},$   (53)

$I_{44}={\displaystyle \underset{1}{\overset{2}{\int }}{p}_{44}{V}_{44}={{{\rm Z}}_{44}|}_1^2=m_{(0)44}{c}^2\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right).}$   (54)

As seen, the relation (54) defines the energy of substance in the whole object under study minus the energy of substance in the surface layer of the object.

$p_{11}d{V}_{11}=p_{11}{V}_{0}d{\epsilon }_{11}={\mu }_{11}{V}_{0}d{\epsilon }_{11};{\mu }_{11}=\frac{\delta \left(\frac{{\zeta }_{(0)11}}{\sqrt{1-{\beta }^2}}\right)}{\delta V_{(0)11}};V_{(0)11}=V_0{\epsilon }_{11};$   (55)

$\frac{\delta {\zeta }_{(0)11}{\left(\sqrt{1-{\beta }^2}\right)}^{-1}}{\delta V_{(0)11}}d{V}_{(0)11}=d\frac{{\zeta }_{(0)11}}{\sqrt{1-{\beta }^2}}=d{{\rm Z}}_{11},$   (56)

${\displaystyle \underset{1}{\overset{2}{\int }}{p}_{11}d{V}_{11}}={{{\rm Z}}_{11}|}_1^2={\zeta }_{\left(0\right)11}\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right),$   (57)

Where ${\zeta }_{(0)11}$  is the energy expended on the increment of the hypercube volume in the direction X₁ at rest.

We can formally represent the expression (54) in another form using the 4D-force $F_1^{(4)}$ (N) and this force action distance. Then we can, in turn, write down

$p_{1}d{V}_1=F_1^{(4)}{S}_{0}d{x}_1=\frac{F_1^{\text{'}}-i\frac{v}{c}{F}_{\tau }^{\text{'}}}{\sqrt{1-{\beta }^2}}{S}_{0}d{x}_{(0)1}\sqrt{1-{\beta }^2},$   (58)

Where $F_1^{\text{'}}$  is the component of the force $F_1^{(4)}$  in the direction X₁ in the moving reference frame; $F_{\tau }^{\text{'}}$  the component of the force $F_1^{(4)}$  in the direction 4.

However it is not convenient to use the expressions of the type (58) for solving our problems, therefore further we will use the expressions of the type (52)-(56).

$p_{22}d{V}_{22}=p_{22}{V}_{0}d{\epsilon }_{22}={\mu }_{22}{V}_{0}d{\epsilon }_{22};{\mu }_{22}=\frac{\delta \left(\frac{{\zeta }_{(0)22}}{\sqrt{1-{\beta }^2}}\right)}{\delta V_{(0)22}},$   (59)

$\frac{\delta {\zeta }_{(0)22}{\left(\sqrt{1-{\beta }^2}\right)}^{-1}}{\delta V_{(0)22}}d{V}_{(0)22}=d\frac{{\zeta }_{(0)22}}{\sqrt{1-{\beta }^2}},$   (60)

${\displaystyle \underset{1}{\overset{2}{\int }}{p}_{22}d{V}_{22}}={{{\rm Z}}_{22}|}_1^2={\zeta }_{(0)22}\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right),$   (61)

The analogous expressions will be obtained for the case $p_{33}d{V}_{33},p_{12}d{V}_{12}=p_{21}d{V}_{21},p_{13}d{V}_{13}=p_{31}d{V}_{31},$   and so on.

If our system is closed one then all its components of the kind $p_{14}d{V}_{14}=p_{41}d{V}_{41},p_{24}d{V}_{24}=p_{42}d{V}_{42},p_{43}d{V}_{43}=p_{34}{V}_{34}$ will be equal to zero.

Now we should obtain the expressions of the work connected with surface tension, i.e., with

$W={\displaystyle \underset{1}{\overset{2}{\int }}\sigma dS}$ .  (62)

As we have seen above, the work of the surface tension is a function of the observation angle of the object under study (Figures 1 & 2). However, the cases represented on the figures are the simplest. A more complicated case is represented on Figure 3.¹²

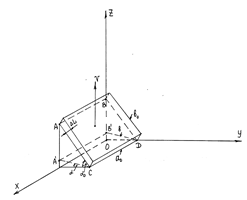
Figure 3 Object under investigations in case velocity v is not parallel and not perpendicular to the interfacial region. A'B'DC denoted by the dashed line is a transition region between contacting phases, as V→ c(ΔL→ 0); a₀ and b₀ are the length and width of the surface for v=0; is the width of the same surface for V→ c.

As seen from Figure 3, the work done by the surface tension depends (the work) on the location of the observer in the laboratory reference frame. If the coordinate axis Y is an observation line at the moment $t_0$ , the observation angle $\theta =\pi /2$ , and the observer is removed to very long distance ΔY from the object, then ${\left(B^{\text{'}}D\right)}^2={\left(0B^{\text{'}}\right)}^2+{\left(0D\right)}^2$ , as $v\to с,$  and we have two areas: the first area is parallel to the velocity of the object movement v, the second one is perpendicular to it. Evidently, the first area depends on the velocity according to the law $S=S_0\sqrt{1-{\beta }^2},$ where $S_0$ is the area at $v=0$ . The second one is independent of v. The first area shows what part of the area of the flat object ABCD depends on v.

Evidently, if we turn our object horizontally by an angle, then we shall already have three projections of the object on the planes formed by the coordinate axes. The areas of two of them will vary according to the above law; the third area will be independent of the velocity v for our observer. However, in the most common cases the object under study has a bent surface. What to do?

In this case we can break down the surface of the object into infinitely great numbers of infinitely small flat elements. The area of each element has projections on the planes formed by the coordinate axes. Taking that into consideration, we can solve the problem connected with the work of surface tension when the surface of the object is bent. In this case the work can be represented as done by surface tension on three planes which are mutually perpendicular. Two planes are parallel to, the third one is perpendicular. Therefore the areas, lying in the parallel planes, will vary in proportion to $\sqrt{1-{\beta }^2}$  as $v\to с$ ; in turn, the areas, lying in perpendicular plane, will not vary under these conditions. Now, having given the all needed explanations, we can represent the expressions for the work of the surface tension forces having begun with the component ${\sigma }_{44}$ being in the planes formed by the coordinate axes.

${\sigma }_{44}d{S}_{\perp }={\rho }_{\perp }{S}_{\perp }d{\epsilon }_{44};$   (63)

${\rho }_{\perp }=\frac{\delta \left(\frac{m_{(0)\perp }{с}^2}{\sqrt{1-{\beta }^2}}\right)}{\delta S_{\perp }};\frac{\delta m_{0\perp }{c}^2{\left(\sqrt{1-{\beta }^2}\right)}^{-1}}{\delta S_{(0)\perp }}{d}_4{S}_{(0)\perp }=d_4\frac{m_{0\perp }{c}^2}{\sqrt{1-{\beta }^2}};$   (64)

$I_2={\displaystyle \underset{1}{\overset{2}{\int }}{\sigma }_{44}d{S}_{(0)\perp }=}{{{\rm M}}_{0\perp }{c}^2|}_1^2=\frac{m_{0\perp }{c}^2}{\sqrt{1-{\beta }^2}}-m_{0\perp }{c}^2=m_{0\perp }{c}^2\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right);$   (65a)

$\Delta S_{\perp }=\Delta x_{(0)2}\Delta x_{(0)3}\frac{\Delta t_0}{\sqrt{1-{\beta }^2}},$   (65b)

Where $S_{(0)},S_{(0)\perp }$ are the values of the 3D-space-time object, the spatial area of which is perpendicular to the velocity $v<<c$ and as $v\to с$ ; ${\rho }_{(0)\perp }$ is the specific density per time unit (g·cm^-2∙s^-1) of substance in this object; $m_{0\perp }$ the substance mass in the surface layer located perpendicularly to the velocity.

In turn, we obtain the expressions for the work of the surface tension forces for the planes parallel to the velocity v:

${\sigma }_{44}d{S}_{(0)}{}_{//}={\rho }_{//}{c}^{2}d{S}_{(0)//}=\frac{{\rho }_{(0)//}{c}^2}{\sqrt{1-{\beta }^2}}{S}_{(0)//}d{\epsilon }_{44};$   (66)

${\rho }_{//}=\frac{\delta \left(\frac{m_{0//}}{\sqrt{1-{\beta }^2}}\right)}{\delta S_{(0)//}};\frac{\delta (m_{0//}{c}^2/\sqrt{1-{\beta }^2})}{\delta S_{(0)//}}{d}_4{S}_{(0)//}=d_4(m_{0//}{c}^2/\sqrt{1-{\beta }^2});$   (67)

$I_3={\displaystyle \underset{1}{\overset{2}{\int }}{\sigma }_{44}d{S}_{(0)//}=}{{{\rm M}}_{//}|}_1^2=\frac{m_{0//}{c}^2}{\sqrt{1-{\beta }^2}}-m_{0//}{c}^2=m_{0//}{c}^2\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right);$   (68)

$\Delta S_{//}=\Delta x_{(0)1}\sqrt{1-{\beta }^2}\Delta x_{(0)2}\frac{\Delta t_0}{\sqrt{1-{\beta }^2}}=\Delta S_{(0)//}$   (69a)

And

$\Delta S_{//}=\Delta x_{(0)1}\Delta x_{(0)3}\Delta t_0=\Delta S_{(0)//},$   (69b)

where $S_{(0)//},S_{//}$  are the volumes of the 3D-space-time object, the spatial areas of which is parallel to the velocity $v<<c$ and as $v\to с$ ; ${\rho }_{(0)//}$ is the specific density per time unit (g·cm^-2∙s^-1) of substance in this object; $m_{0//}$ the substance mass in the surface layer located parallel to the velocity v at rest; the values $\Delta S_{//}$ in (69a) and (69b) are not equal to one another in common case. Evidently, the increments of the kind (63) and (66) are already in the dependence (43) therefore they will not further be taken into consideration.

For the real work of the surface tension forces we have the following relations (the plane is perpendicular to the velocity v):

${\sigma }_{23}d{S}_{\perp }={\sigma }_{32}d{S}_{\perp }={\rho }_{\perp }\frac{S_{(0)\perp }}{\sqrt{1-{\beta }^2}}d{\epsilon }_{23};$   (70)

${\rho }_{\perp }=\frac{\delta {\xi }_{23}}{\delta S_{\perp }}=\frac{\delta \left(\frac{{\xi }_{(0)23}}{\sqrt{1-{\beta }^2}}\right)}{\delta \left(\frac{S_{(0)\perp }}{\sqrt{1-{\beta }^2}}\right)};$   (71)

$\frac{\delta {\xi }_{23}}{\delta S_{\perp }}d{S}_{\perp }=\frac{\delta \left(\frac{{\xi }_{(0)23}}{\sqrt{1-{\beta }^2}}\right)}{\delta \left(\frac{S_{(0)\perp }}{\sqrt{1-{\beta }^2}}\right)}d\frac{S_{(0)\perp }}{\sqrt{1-{\beta }^3}}=d\frac{{\xi }_{(0)23}}{\sqrt{1-{\beta }^2}};$   (72)

${\displaystyle \underset{1}{\overset{2}{\int }}{\sigma }_{23}d{S}_{\perp }}={\frac{{\xi }_{(0)23}}{\sqrt{1-{\beta }^2}}|}_1^2=\Xi {{}_{23}|}_1^2={\xi }_{(0)23}\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right);$   (73)

$\begin{array}{l}\Delta S_{\perp }=\Delta x_{(0)2}\Delta x_{(0)3}\frac{\Delta t_0}{\sqrt{1-{\beta }^2}}=\frac{\Delta S_{(0)\perp }}{\sqrt{1-{\beta }^2}};\\ \frac{F_3\Delta L_3}{\Delta L_2\Delta L_3}+\frac{F_2\Delta L_2}{\Delta L_2\Delta L_3}=\frac{{\sigma }_{23}}{\Delta S_{23}}\end{array}$ ,  (74)

Where ${\sigma }_{23}={\sigma }_{32}$ is the surface tension per time unit on the real surface (X₂X₃), the whose 3D-space-time object (the surface) is perpendicular to the velocity v; $S_{(0)\perp },S_{\perp }$  are the volumes of the 3D-space-time object, the spatial area of which is perpendicular to the velocity $v<<c$ and as $v\to с$   $\delta {\xi }_{(0)23}=\delta {\xi }_{(0)32}$  is the energy expended on the increment of the area perpendicular to the velocity v; $F_2,F_3$  are the surface tension forces in direction 2 and 3 acting (the forces) in the plane perpendicular to the velocity v; $\Delta L_2,\Delta L_3$  distances in directions 2 and 3 on which the forces 2 and 3 are acting.

${\sigma }_{12}d{S}_{//}={\sigma }_{21}d{S}_{(0)//}={\rho }_{//}{S}_{(0)12}d{\epsilon }_{12};$   (75)

${\rho }_{//}=\frac{\delta {\xi }_{//}}{\delta S_{(0)12}}=\frac{\delta \left(\frac{{\xi }_{(0)12}}{\sqrt{1-{\beta }^2}}\right)}{\delta S_{(0)12}};$   (76)

$\frac{\delta \left(\frac{{\xi }_{(0)12}}{\sqrt{1-{\beta }^2}}\right)}{\delta S_{(0)12}}d{S}_{(0)12}=d\frac{{\xi }_{(0)12}}{\sqrt{1-{\beta }^2}};$   (77)

${\displaystyle \underset{1}{\overset{2}{\int }}{\sigma }_{12}d{S}_{(0)12}={\frac{{\xi }_{(0)12}}{\sqrt{1-{\beta }^2}}|}_1^2=}{{\Xi }_{12}|}_1^2={\xi }_{(0)12}\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right);$   (78)

$\Delta S_{//}=\Delta x_{(0)1}\Delta x_{(0)2}\Delta t_0=\Delta S_{(0)//};$   (79)

$\frac{F_1\Delta L_1}{\Delta L_1\Delta L_2}+\frac{F_2\Delta L_2}{\Delta L_1\Delta L_2}=\frac{{\sigma }_{12}}{\Delta S_{12}}$ ,  (80)

Where ${\sigma }_{12}={\sigma }_{21}$ is the surface tension per time unit on the real surface (X₁X₂), the whose 3D-space-time object is parallel to the velocity v; $S_{(0)\perp },S_{\perp }$  are the volumes of the 3D-space-time object, the spatial area of which is parallel to the velocity $v<<c$ and as $v\to с$   $\delta {\zeta }_{(0)12}=\delta {\zeta }_{(0)21}$  is the energy expended on the increment of the area parallel to the velocity v; $F_1,F_2$  are the surface tension forces in directions 2 and 3 acting (the forces) in the plane parallel to the velocity v; $\Delta L_1,\Delta L_2$  distances in directions 2 and 3 on which the forces 1 and 2 are acting.

The case ${\sigma }_{13}={\sigma }_{31}$ does not fundamentally different from the previous one. Now we are going to convert the heat. First of all, we should take into consideration that in this case we use 4D-velocity including the velocities of microparticles. In 3D-formalism the energy of acceleration varies in inverse proportion to $\sqrt{1-{\beta }^2}$ , and this energy has also to convert in heat in the inverse proportion to $\sqrt{1-{\beta }^2}$ for the observer being in the laboratory reference frame at rest. Therefore we have for the relativistic heat

$Q_{(T)}={\displaystyle \underset{1}{\overset{2}{\int }}d{Q}_{(T)}^{\kappa \lambda }{g}_{\kappa \lambda }};\kappa ,\lambda =1,2,3,4;\kappa \ne \lambda$ ,  (81)

Where $Q_{(T)}^{\kappa \lambda }$  is the tensor of the relativistic heat; $g_{\kappa \lambda }$  the fundamental tensor of rank 2.

$Q_{(T)}=\frac{Q_{0(T)}}{\sqrt{1-{\beta }^2}},$   (82)

Where $Q_{0(T)}$  is the $Q_{(T)}$ at rest.

To some extent, the quantity $Q_{(T)}$ is similar to the term $(1/c)q^{\alpha }D{u}_{\alpha }$  in the above expression (38). Such terms can be only in relativistic thermodynamics.

From the aforesaid on the thermo dynamical heat $Q_{(s)}$ including the expressions (27)-(31), we can represent this quantity as

$Q_{(s)}={\displaystyle \underset{1}{\overset{2}{\int }}d{Q}_{(s)}^{\kappa \lambda }{g}_{\kappa \lambda }};\kappa ,\lambda =1,2,3,4;\kappa \ne \lambda$ ,  (83)

And

$Q_{(s)}=\frac{Q_{0(s)}}{\sqrt{1-{\beta }^2}}.$   (84)

Can we obtain expressions similar to the relations (81) - (84) for the internal energy not taking into consideration the expressions obtained above for 4D-work and heat? Evidently, no, since we cannot determine the increment of internal energy without the calculation of the energy put into the system or removed from it by means of work and heat. The internal energy cannot accurately be determined by physical devices. Taking into consideration the all above expressions for the transformation of heat and work in 4D formalism, we can conclude that the internal energy U has to transform under relativistic conditions as

$U=\frac{U_0}{\sqrt{1-{\beta }^2}}$ ,  (85)

And the first principle of thermodynamics in 4D-formalism can be written as

$\begin{array}{l}D\frac{E}{\sqrt{1-{\beta }^2}}=D\frac{Q_{0(s)}}{\sqrt{1-{\beta }^2}}+D\frac{Q_{0(T)}}{\sqrt{1-{\beta }^2}}+D\frac{m_0{c}^2}{\sqrt{1-{\beta }^2}}+D{\displaystyle \sum _{\kappa ,\lambda =1,2,3}({\zeta }_{(0)\kappa \lambda }/\sqrt{1-{\beta }^2})}+\\ -D{\displaystyle \sum _{\kappa ,\lambda =1,2.3}({\xi }_{(0)\kappa \lambda }}/\sqrt{1-{\beta }^2})+D\frac{m_0{v}_1^2}{\sqrt{1-{\beta }^2}}.\end{array}$ ,  (86)

Where $E\left(=U_0+E_{kin}\right)$ is the energy of the system, D is differential sign in 4D-formalism.

Obtaining (86), we have taken into consideration the relations (20), (41), (43), (55), (59), (70), (75) and the equality $I_4=I_{44}+I_2+I_3$ .

The relation (86) is quite correct in the velocity interval 0-v of the object under study. The both sides of its transform identically under relativistic conditions - we do not come to absurdity, as $v\to c$ , since the both sides of these relations become infine.

The law (86) is the first 4D-principle of thermodynamics without taking into consideration of the work of the electromagnetic forces, and in case the vector v of the system motion is parallel to the coordinate axis X₁. The relation (86) is the fundamental one, its left and right sides transform identically under relativistic conditions but we can determine the transformation of the left side of the relation only by means of the transformation of the right side. In the general case the fundamental nature of this or that dependence can be determined by means of the principle of two observers. The principle is formulated below anticipating by an example. Let a process of heat transfer take place in our system. In the simplest case the process can be described in several ways: first, by the formula of heat transfer $I_q$ (J∙cm^-2 ∙s^-1) Fourier, second, by the formula of the heat transfer taken from irreversible thermodynamics,¹³ third, by Veitsman’s formula.¹² Here they:

$I_q=-\lambda \frac{\partial T}{\partial x},$   (87)

$I_q=-a_q\frac{\nabla T}{T},$   (88)

$I_{\alpha }=-D_{\alpha \beta }\frac{\partial q}{\partial x_{\beta }};\alpha ,\beta =1,2,3;\alpha =\beta ,$   (89)

Where λ is the thermal conductivity coefficient (J∙cm^-1∙s^-1∙grad^-1; scalar); $a_{{}_q}$ the phenomenological thermal conductivity coefficient (J∙cm^-1∙s^-1; scalar); $D_{\alpha \beta }$  the coefficient of thermal diffusion (cm²∙s^-1; tensor of rank 2); q the specific density of heat (J∙cm^-3).

Let two observers be in a laboratory reference frame. The first observer is measuring the quantities being on the left side of the expressions (87)-(89) by devices under relativistic conditions. In turn, the second observer is measuring the parameters being on the right side of these relations under the same ones. If these measured quantities are substituted in the above expressions, then we do not lead to absurdity only in the case (89).¹² In the cases (87) and (88) the left sides of these formulae will transform differently from their right ones. It means that relations (87) and (88) are not the fundamental physical dependences.

Now we can formulate the principle of two observers: “A physical dependence will be truly fundamental one only in case the parameters, obtained by the first and the second independent observers for the left and right sides of this dependence, do not lead to absurdity and contradictions under relativistic conditions by being accordingly substituted in the left and right sides of the physical formula”.

4D-space component

$G_{sp}=u\frac{\left(U_0+{\displaystyle \sum _{\alpha ,\beta =1,2,3}{{\rm Z}}_{(0)\alpha \beta }-{\displaystyle \sum _{\kappa ,\lambda =1,2,3}{\Xi }_{(0)\kappa \lambda }}}\right)}{{с}^2\sqrt{1-{{\rm B}}^2}}, \kappa \ne \lambda$ ,  (90)

And 4D-time component

$G_t=\frac{i}{c}\left(U+{\displaystyle \sum _{\alpha ,\beta =1,2,3}{{\rm Z}}_{\alpha \beta }}-{\displaystyle \sum _{\kappa ,\lambda =1,2,3}{\Xi }_{\kappa \lambda }}\right), \kappa \ne \lambda$ ,  (91)

Forms an invariant quantity

$G=\frac{i}{c}\left(U_{(0)}+{\displaystyle \sum _{\alpha ,\beta =1,2,3}{{\rm Z}}_{(0)\alpha \beta }}-{\displaystyle \sum _{\kappa ,\lambda =1,2,3}{\Xi }_{(0)\kappa \lambda }}\right), \kappa \ne \lambda$ ,  (92)

Where ${\rm B}=u/c$ , u is the 4-velocity vector in real space.

As seen above, the temperature of the system is present in the first principle of thermodynamics in a latent form - by means of the second principle of thermodynamics

$\delta S=\frac{\delta Q}{T},$   (93)

Where S is the entropy, which is Lorentz-invariant according to Planck, i.e.,

$S=S_0.$   (94)

 If we write down the transformation of heat Q under relativistic conditions as

$Q=Q_0\sqrt{1-{\beta }^2},$   (95)

Then the temperature has to transform under these conditions according to (21), i.e., according to M.Planck. However, if we write down the transformation of Q as

$Q=\frac{Q_0}{\sqrt{1-{\beta }^2}}$ ,  (96)

Then the temperature T has to transform under these conditions according to the following formula

$T=\frac{T_0}{\sqrt{1-{\beta }^2}}$ ,  (97)

i.e., according to Ott H⁶ As we have seen above, the relations (96) and (97) do not lead to the absurdity, the relations (21) and (40), on the contrary, do. Where were Planck and Einstein mistaken? We make an attempt to show it starting from (2). Einstein proceeds from Gibb’s equation taken in the form (normal state):

$TdS=dE+pdV-vdG,$   (98)

Where E is the internal energy.

Accelerate adiabatically our system up to the velocity v. Further, integrate (98) term by term from state 1 (v=0) up to state 2 (v→∞):

${\displaystyle \underset{1}{\overset{2}{\int }}TdS={\displaystyle \underset{1}{\overset{2}{\int }}dE+{\displaystyle \underset{1}{\overset{2}{\int }}pdV-{\displaystyle \underset{1}{\overset{2}{\int }}vdG}}}}$ .  (99)

Since $S_0=S$ , then in view of (16)

$E_2-E_1+p_{0}V-p_0{V}_0-\left(U_0+p_0{V}_0\right)\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right)=0.$   (100)