In this paper, the influence of the electric field of co-rotation on the possibility of long holding of micro-particles with dimensions on the order of tens of nm and quasi-equilibrium charge moving along weakly elliptic orbits in the plasma-sphere of the Earth is considered with the help of analytical and numerical methods. It is shown that, unlike the magnetic field, the electric field of co-rotation causes a slow change in the shape of the orbit.

Keywords: electric field, micro-particles, plasma-sphere, magnetic field, submicron sizes, lorentz force

The problems of the dynamics of fine-dispersed particles in near-Earth space (NES) are actively considered for more than 30 years in connection with the problem of manmade pollution of near space by manmade micro-particles (MP). At the same time, the main attention is paid to the determination of the characteristics of man-made MP and the conditions for their injection into NES, capable of long-term holding in near-Earth space. As a result of the conducted researches it was established that the large orbital existence times in the NES can have fairly large particles with dimensions of the order of 1-100μm. At the same time, the fundamental possibility of prolonged holding of manmade particles of submicron sizes in the vicinity of the Earth was questionable, since, as shown by numerical simulation data on the dynamics of particles with dimensions of the order of 0.1-1μm in the NES, the orbital lifetimes of MPs of the indicated sizes, as a rule, when injected at high altitudes by a disturbing effect of the solar pressure force^1,2 and in low Earth orbits - by the residual gas resistance of the upper atmosphere.^3,4 For the first time studies of the dynamics of smaller particles with dimensions less than 0.1μm were carried out by us in.^5,6 Received in_5,6 the results of numerical modeling of the motion of these particles in the Earth's plasma-sphere showed that, in contrast to the previously considered submicron particles with dimensions of the order of 0.1-1μm, particles with dimensions less than 0.1μm (on the order of tens of nm) under certain conditions as a result of disturbing effects on their the movement in the NES of the Lorentz force acting on the electric charge accumulating on the MP from the magnetic and electric fields of near-Earth space is able to be held for a long time in the near-Earth space and may be, therefore, an important factor of manmade pollution of near space.

In connection with the foregoing, it became necessary to carry out fundamental theoretical studies of the conditions for the "capture" of submicron particles in the vicinity of the Earth, including, on the basis of the application of appropriate analytical methods. In the work,⁷ we showed that under certain model assumptions about the number, nature, and method of determining perturbing forces acting on MP, the problem of the dynamics of submicron particles in the plasma-sphere admits a canonical formulation in the form of a Hamiltonian system of equations. In this case a basis for an analytic study of the properties of motion are methods of the qualitative theory of Hamiltonian systems developed in the papers of Kolmogorova AN, Arnold VI and Moser J (the so-called KAM-theory).^8,9 Using well-known methods of KAM-theory, we in^10,11 proved that in the Earth's plasma-sphere, the weakly elliptic orbits of micro-particles with dimensions on the order of tens of nm and a quasi-equilibrium charge retain their shape. However, in the model used in,^10,11 we did not take into account the electric field of co-rotation. In this paper the influence of the electric field of co-rotation on the possibility of prolonged holding of these micro-particles is considered with the help of analytical and numerical methods.

A general condition for the correctness of the canonical formulation of the problem of the motion of a micro-particle in the NES is the possibility of representing all forces acting on the MF in the form:¹²

$F^j=-\nabla V^j\text{ or }{F}_i^j=-\frac{\partial U^j}{\partial x_i}+\frac{d}{dt}\frac{\partial U^j}{\partial {\dot{x}}_i}\text{ (}i=1,2,3)$

Where $V^j=V^j(x_1,x_2,x_3,t)$ - ordinary potential $U^j(x_1,x_2,x_3,{\dot{x}}_1,{\dot{x}}_2,{\dot{x}}_3,t)$  is a generalized potential. When the MP moves at sufficiently high altitudes, the resistance force of the background gas of the upper atmosphere can be neglected and, therefore, the main forces acting on the MP are the gravitational force, the solar pressure force, and the Lorentz force. The velocity-independent gravitational force and the solar pressure force (for the spherical MP) are represented by the usual potentials $V^{gr}$ and $V^{sp}$ . In this case, the Lorentz force acting on the generally variable charge of the MP from the magnetic and electric fields of the NES, as shown by us in,⁷ allows a representation with the help of a generalized potential $U^L$ when the corresponding restrictions on the nature of the change in the charge of the MP in the process of its orbital motion are met, and also on the features of the spatial distribution of the magnetic and electric fields of the NES. The first of these limitations consists in fulfilling the quasi-equilibrium condition of the electric charge of the MP, which is determined by the local values ​​of the parameters of the background plasma and depends only on the current coordinates of the MP,

$Q=Q\left(r\right)$ ,  (1)

Where r is the radius vector of the current position of the MP. The second restriction (on the geometric characteristics of fields) consists of the following:

$B\perp \nabla q$ ,  (2)

$E\parallel \nabla q$ .  (3)

As shown in,⁷ under the conditions (1)-(3), the Lorentz force can be represented by a generalized potential

$U^L=Y_1-\frac{v\cdot Y_2}{c}$   (4)

Where $Y_1$ and $Y_2$ are the scalar and vector coordinate functions that satisfy equations

$\{\begin{array}{c}\nabla Y_1=Q\nabla \phi \\ \mathrm{rot}{Y}_2=Q\mathrm{rot}A\end{array}$ .  (5)

In (5) $\phi$ and A–respectively, the scalar and vector potentials acting on the MP electric and magnetic fields of the NES.

As shown in,⁷ with allowance for (4), the Hamiltonian function describing the dynamics of a micro-particle with a variable charge in the NES is determined by the formula:

$H=\frac{1}{2m}{\displaystyle \sum _{i=1}^3{\left(P_i-\frac{Y_{2i}}{c}\right)}^2}+V^{gr}+V^{pr}+Y_1$ ,  (6)

Where the components of the generalized momentum vector are $P_i=m{\dot{x}}_i+\frac{Y_{2i}}{c}$ .

In⁷ by the results of numerical simulation, it is shown that when the MP moves in the terrestrial plasma-sphere, the condition (1) is fulfilled for micro-particles with radii of more than 0.01μm, whose orbits pass at distances greater than one and a half radii of the Earth from its surface.

The fulfillment of the same geometric conditions (2) & (3) follows from the features of the spatial distribution of the plasma in the plasma-sphere of the Earth. This distribution is described, as is well known, by the model of a two-component plasma,¹³ consisting of a "cold" component with a density $n_{cold}$  and temperature $T_{cold}$  and "hot" components with density $n_{hot}$  and temperature $T_{hot}$ . In this case, the total density of the plasma $n=n_{cold}+n_{hot}$ . Options $n_{cold}$ , $T_{cold}$ and $n_{hot}$ , $T_{hot}$  are given by the expressions [Hill, J.R., and Wipple, E.C.1985]:

$n_{cold}=\{\begin{array}{l}{n}^{\ast }-1,{{\rm T}}^{\ast }>1eV\\ n^{\ast },{{\rm T}}^{\ast }<1eV\end{array}{{\rm T}}_{cold}=\{\begin{array}{l}1∍B,{{\rm T}}^{\ast }>1eV\\ {{\rm T}}^{\ast },{{\rm T}}^{\ast }<1eV\end{array}$   (7)

$n_{hot}=\{\begin{array}{l}1{\text{CM}}^{-3},{{\rm T}}^{\ast }>1eV\\ 0,{{\rm T}}^{\ast }<1eV\end{array}{{\rm T}}_{hot}={{\rm T}}^{\ast },{{\rm T}}^{\ast }>1eV$   (8)

In (7) and (8), the functions $n^{\ast }\left(L\right)$  and $T^{\ast }\left(L\right)$  are defined by the formulas: 

$n^{\ast }\left(L\right)={10}^{\frac{\left(15-L\right)}{3.5}},{\text{ sm}}^{\text{-3}}\text{,}{T}^{\ast }\left(L\right)=0.09239L^{2.7073},\text{ eV}$

Where L is parameter of the local magnetic shell. The equilibrium charge of the body, being a function of local density and temperature, does not depend, therefore, on the longitudinal coordinate along the magnetic field line, which corresponds to the fulfillment of condition (2). In this case $Q=Q(L)$ . The main contribution to the geo-electric field at altitudes of the plasma-sphere is made, as we know, by the electric field of co-rotation $E_{cor}=\frac{1}{c}\left(r\times \Omega \right)\times B$ , where $\Omega$ is the angular velocity vector of the Earth's rotation. It is easy to verify that if the geomagnetic field is approximated by a dipole magnetic field with a magnetic moment anti-parallel to the Earth's rotation axis, the co-rotation field satisfies the necessary condition (3).

We make a number of additional simplifying assumptions about the dimensions of the MP, which forms its material and the orbits of the MP in the plasma-sphere. We confine ourselves to the consideration of MPs with radii of the order of some hundredths of micron. For particles of these dimensions, the efficiency of light pressure at the MP is small¹⁴ and the influence of the solar pressure forces on the movement of MP in the NES can be neglected. We will consider the MP from a material with a low photoemission yield. For such particles, in the plasma conditions of the plasma-sphere, the potential of the MP (and, accordingly, its charge) varies insignificantly when passing through the Earth's shadow. Thus, in the case under consideration, the dynamic shadowing effect of a part of the orbit of the MP can also be neglected. Finally, we restrict our attention to the cases of the motion of MPs along weakly elongated orbits (with eccentricities less than 0.3-0.4) lying in the near Earth part of the plasma-sphere, with perigee height greater than the Earth's radius. We note that in these orbits one can neglect the disturbing effect of electric field of convection on the motion of the MP.

Under the assumptions made, the problem under consideration reduces to the problem of the motion of a MP with a variable electric charge in the superposition of the central gravitational field and the Lorentz force acting on the electric charge of the MP from the side of the dipole magnetic field of the Earth and the electric field of co-rotation. We note that the dipole approximation is correct for geocentric distances from one and a half to ten Earth radii.¹⁵

We will work in a spherical coordinate system $r,\vartheta ,\phi$  with the origin in the center of the Earth and the polar axis passing through the south magnetic pole. In this case, the Hamiltonian function (8) can be written thus:

$H=\frac{1}{2m}\left[P_r^2+P_{\vartheta }^2+\frac{1}{r^2{\sin }^2\vartheta }{\left(P_{\phi }-\frac{Y_{2\phi }r\sin \vartheta }{c}\right)}^2\right]-\frac{m{\mu }_E}{r}+Y_1$ ,  (9)

Where ${\mu }_E$ -geocentric gravitational constant. The magnitude of the electric charge $Q(L)$ is determined as a result of a numerical solution of the balance equation of the charging currents

$J_{tot}({\Phi }_{eq})\equiv J_p^e+J_p^i+J_{ph}+J_{field-emission}=0$ ,  (10)

Here ${\Phi }_{eq}=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{P}$  is equilibrium potential, $J_p^e$  is the current of plasma electrons, $J_p^i$  is the total current of plasma ions, $J_{ph}$  is the current of photoelectrons and $J_{field-emission}$  is current of field emission, ${\epsilon }_0$  is electrical constant and R is radius of micro-particle. In the plasma-sphere, the equilibrium charge is negative, and therefore the charging currents in (10) are determined by the expressions in.⁷

We approximate the value of the MP charge by the following polynomial

$Q\left(L\right)=Q_0\left[1+{\displaystyle \sum _{k=1}^n{\xi }_k{\left(\frac{L-L_0}{L}\right)}^k}\right]$ ,  (11)

Where $Q_0$  is charge at $L=L_0$ . Values of the coefficients ${\xi }_k$  can be obtained by substituting expression (11) into equation (10). It is possible to show¹¹ that an increase in the degree of a polynomial significantly improves the accuracy of approximation even for a greater interval of values L.

To obtain expressions for $Y_{2\phi }$  and $Y_1$  we use dipole coordinates $L,\Phi ,M$ ,¹⁶ formula (11) for the charge and the Lamé coefficients for the dipole coordinates

$h_L=\frac{R_E}{(1+\Lambda )\cdot {(1+4\cdot \Lambda )}^{1/2}},h_{\Phi }=\frac{R_E\cdot L}{{(1+\Lambda )}^{3/2}}{h}_{{\rm M}}=\frac{R_E\cdot L^3}{{(1+\Lambda )}^{5/2}\cdot {(1+4\cdot \Lambda )}^{1/2}}$

Where $\Lambda =ct{g}^2\vartheta ,R_E$  is the radius of the Earth.

Then

$Y_{2\phi }{h}_{Ф}=-Q_0{B}_E{R}_E^2{{\displaystyle {\displaystyle \int \left[1+{\displaystyle \sum _{k=1}^n{\xi }_k{\left(\frac{L-L_0}{L}\right)}^k}\right]\frac{1}{L^2}\mathrm{d}L}}}^{\text{}}$ ,  (12)

$Y_1=Q_0{h}_L{{\displaystyle {\displaystyle \int \left[1+{\displaystyle \sum _{k=1}^n{\xi }_k{\left(\frac{L-L_0}{L}\right)}^k}\right]E_{kor}\mathrm{d}L}}}^{\text{}}$ ,  (13)

Here $B_E=\frac{M_E}{R_E^3}$  is induction of a magnetic field in the plane of the magnetic equator ($\vartheta =\frac{\pi }{2}$ ) on the surface of the Earth,¹⁶ $M_E$  is the magnetic moment of the Earth, $E_{cor}=-\frac{C\cdot R_E}{r^2}$  is the intensity of the co-rotation field, C =92kV.

Without loss of generality, in order to simplify the expressions obtained, we confine ourselves to the case of a small eccentricity of the unperturbed Keplerian elliptic orbit and, correspondingly, the first three terms in the polynomial (11). Then from (12) and (13) we obtain expressions for generalized potentials

$Y_{2\phi }=\frac{Q_0{B}_E{R}_E}{L{\sin }^3\vartheta }\left[\frac{1+{\xi }_1+{\xi }_2}{L}-\frac{L_0\left({\xi }_1+2{\xi }_2\right)}{2L^2}+\frac{{\xi }_2{L}_0^2}{3L^3}\right]$ ,

$Y_1=\frac{Q_0\cdot С}{\sin \vartheta \cdot \sqrt{1+3{\cos }^2\vartheta }}\left[\frac{1+{\xi }_1+{\xi }_2}{L}-\frac{L_0\left({\xi }_1+2{\xi }_2\right)}{2L^2}+\frac{{\xi }_2{L}_0^2}{3L^3}\right]$ ,

Which in spherical coordinates have the form

$Y_{2\phi }=-\frac{Q_0{M}_E\sin \vartheta }{r}\left[\frac{1+{\xi }_1+{\xi }_2}{r}-\frac{R_E{L}_0{\sin }^2\vartheta \left({\xi }_1+2{\xi }_2\right)}{2r^2}+\frac{{\xi }_2{L}_0^2{R}_E^2{\sin }^4\vartheta }{3r^3}\right]$ ,

$Y_1=\frac{Q_0СR_E\sin \vartheta }{\sqrt{1+3{\cos }^2\vartheta }}\left[\frac{1+{\xi }_1+{\xi }_2}{r}-\frac{L_0{R}_E{\sin }^2\vartheta \left({\xi }_1+2{\xi }_2\right)}{2r^2}+\frac{{\xi }_2{L}_0^2{\sin }^4\vartheta R_E^2}{3r^3}\right]$ .

If the co-rotation field is not taken into account, then, as shown in,¹¹ the Hamiltonian of the problem can be represented as the sum

$H=H_0+H_1+H_2$ ,  (14)

Where

$\begin{array}{l}{H}_0=\frac{1}{2m}\left(P_r^2+P_{\vartheta }^2+\frac{P_{\phi }^2}{r^2{\sin }^2\vartheta }\right)-\frac{m{\mu }_E}{r},H_1=\frac{P_{\phi }{Q}_0{M}_E{\eta }_1}{m{r}^{3}c},\\ H_2=\frac{Q_0^2{M}_E^2{\sin }^2\vartheta {\eta }_2}{2m{c}^2{r}^4}+O\left(\frac{1}{r^4}\right),\end{array}$

${\eta }_1=1+{\xi }_1+{\xi }_2,{\eta }_2=1+{\xi }_1^2+2{\xi }_2+2{\xi }_1+{\xi }_2^2+2{\xi }_1{\xi }_2-{\eta }_3,{\eta }_3=\frac{P_{\phi }{L}_0{R}_{E}c}{Q_0{M}_E}\left({\xi }_1+2{\xi }_2\right).$

The first term $H_0$  corresponds to the Hamiltonian of the body motion problem in the Newtonian gravitational field, and the second and third terms are caused by the perturbing action of the magnetic field. For a purely gravitational problem, the osculating elements of the orbit are known to remain constant over an infinite time interval. As shown in,¹¹ act of $H_1$  and $H_2$  leads to small oscillations of the osculating elements within narrow intervals of quantities. In this connection, the question arises: how can the orbit behavior change the influence of the co-rotation field.

Substituting in $Y_1$ (9) we obtain:

$\begin{array}{l}H=H_{cor}=H_0+H_1+H_2+\\ \frac{Q_0\cdot С\cdot R_E\cdot \sin \vartheta }{\sqrt{1+3{\cos }^2\vartheta }}\left[\frac{1+{\xi }_1+{\xi }_2}{r}-\frac{L_0\cdot R_E\cdot {\sin }^2\vartheta \left({\xi }_1+2{\xi }_2\right)}{2\cdot r^2}+\frac{{\xi }_2\cdot L_0^2\cdot {\sin }^4\vartheta \cdot R_E^2}{3\cdot r^3}\right].\end{array}$   (15)

In contrast to the previous case, the transition to the Delaunay variables $L_D,G_D,H_D,l_D,g_D,h_D$ ¹⁷ does not lead to a simple decomposition $H_{cor}=H_{0,cor}+H_{1,cor}+H_{2,cor}$  with $H_{0,cor}$ , depending only on $L_D$ . Therefore, in the general case ($\vartheta \ne \frac{\pi }{2}$ ) even in the zero order of the expansion of the Hamiltonian with respect to a small parameter, the conservation of the basic orbital parameters is not ensured. However, when $\vartheta =\frac{\pi }{2}$  for the Hamiltonian $H_{cor}$  we can enter an effective parameter, ${\mu }_{E,ef}={\mu }_E-\frac{Q_0\cdot C\cdot R_E}{m}(1+{\xi }_1+{\xi }_2)$ which allow recording $H_{0,cor}$  in the same form as $H_0$  in the formula (14), in this case

$H_{1,cor}=-\frac{Q_{0}C{L}_0{R}_E^2\left({\xi }_1+2{\xi }_2\right)}{2r^2},$

$H_{2,cor}=\frac{{\xi }_2{Q}_{0}C{L}_0^2{R}_E^3}{3r^3}+\frac{P_{\phi }{Q}_0{M}_E{\eta }_1}{m{r}^{3}c}+\frac{Q_0^2{M}_E^2{\eta }_2}{2m{c}^2{r}^4}+O\left(\frac{1}{r^4}\right)$

That is, when moving in the equatorial plane, taking into account the co-rotation field reduces to the conservation in the zeroth approximation of the semi major axis, eccentricity and inclination angle. Member accounting $H_{2,kor}$ , proportionate $r^{-3}$ , leads to small oscillations of the semi major axis and eccentricity, as we have shown earlier in,¹¹ for the disturbing action of the magnetic field. But the member $H_{1,kor}$ , proportional $r^{-2}$ , stipulates the existence of secular changes in orbital parameters.

To confirm the obtained analytical results, numerical experiments were carried out to simulate the motion of micro-particles in the terrestrial plasma-sphere with radii of the order of some hundredths of micron. Simulation of MP motion was carried out on the basis of a numerical solution of the equations of motion of micro-particles with a locally equilibrium electric charge, determined from the solution of the current balance equation (10), under the same simplifying assumptions under which the Hamiltonian (15) was written. As an example, Figures 1 & 2 shows the calculated dependencies on time, respectively, of the large semi major axis and the eccentricity of the MP orbit from carbon with a radius of 0.033μm injected into the NES at the perigee point of the elliptical orbit with parameters: perigee altitude 9000km, an angle of inclination of $0^0$ , starting speed 5,449km/s, longitude of the ascending node of ${180}^0$ , ascending node-perigee angle of ${270}^0$ . The simulation was carried out at a time interval of 720 hours (1 month), and in this case only two forces were taken into account: gravitational and co-rotation, and did not take into account the effect of shadowing part of the orbit. As can be seen from the data in Figures 1 & 2, in the case under consideration the semi major axis and the eccentricity of the orbit of the MP, as predicted, almost monotonously increase with time. Figures 3–5 show the results of numerical simulation for the same initial conditions, but obtained on the basis of a joint solution of the equation of motion and the equation of micro-particle charging. These results show that there are no fundamental differences in the behavior of the semi major axis and the eccentricity of the orbit for the cases of equilibrium and non-equilibrium charges of MP. The results of the calculations presented in Figures 6–10, allow us to estimate the influence of the initial angle of inclination and shading of a part of the orbit on the character of the orbital parameter change. A nonzero initial angle of inclination causes oscillations of the semi major axis, eccentricity and inclination angle, a monotonic increase in the mean valueand the appearance of an additional frequency of the oscillations of the potential of the MP, which coincides with the frequency of oscillations a, i and e. The shadowing effect of a part of the orbit does not significantly change the behavior of the potential of the MP, the eccentricity and the inclination angle of the orbit, and lubricates the clear character of the behavior of the semi major axis (Figure 8). Numerical calculations for other radii of MP and initial conditions for its injection, also satisfying the conditions of application of the model in question, give similar results.

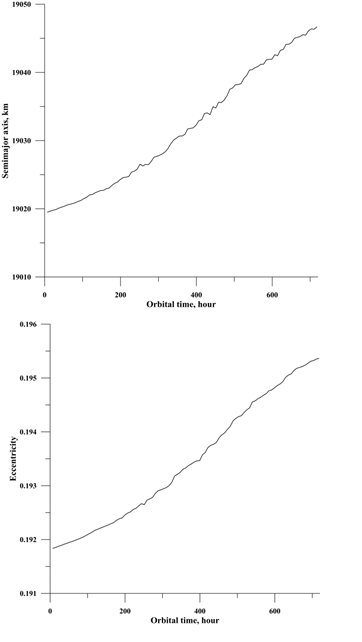
Figure 1 & 2 Dependences of the semi major axis (1) and the eccentricity (2) of the orbit of the micro-particle with locally equilibrium electric charges on time moving in the equatorial plane for the case of the action of only 2 forces: the gravitational and the Lorentz force component due to the co-rotation field.

Figure 3 & 4 Dependences of the semi major axis (3) and the eccentricity (4) of the orbit of the micro-particle with non-equilibrium electric charges on time moving in the equatorial plane for the case of the action of only 2 forces: the gravitational and the Lorentz force component due to the co-rotation field.

Figure 5 Dependence of the electric potential of a micro-particle with non-equilibrium electric charges on the time moving in the equatorial plane for the case of the action of only two forces: the gravitational and the component of the Lorentz force due to the co-rotation field.

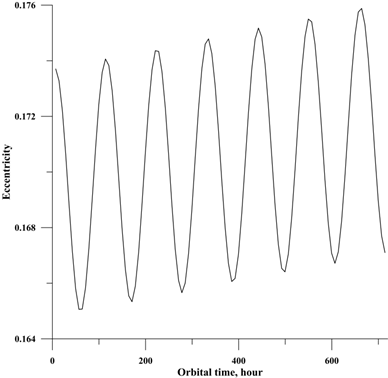
Figure 6 Dependence of the eccentricity of the orbit of a micro-particle with non-equilibrium electric charges on time injected with an initial inclination of 30 degrees for the case of the action of only 2 forces: the gravitational and the Lorentz force component due to the co-rotation field (without shading).

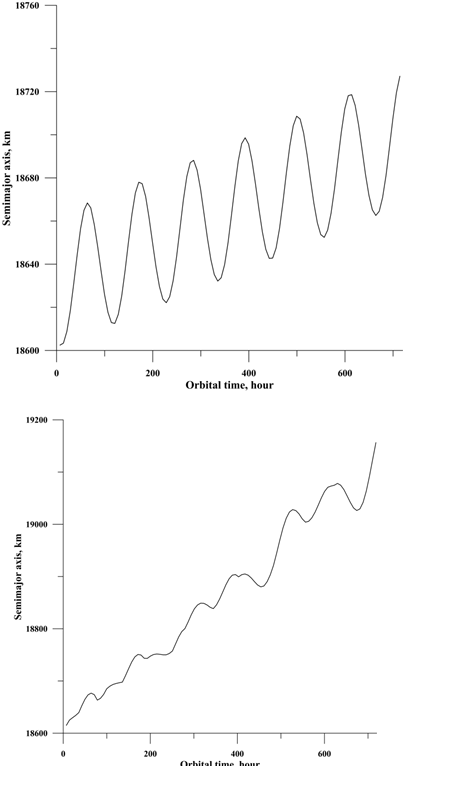
Figure 7 & 8 Dependences of the semi major axis of the micro-particle orbit with the non-equilibrium electric charges on time injected with an initial inclination of 30 degrees for the case of the action of only 2 forces: the gravitational and the Lorentz force component due to the co-rotation field (7 without shading, 8 with shading).

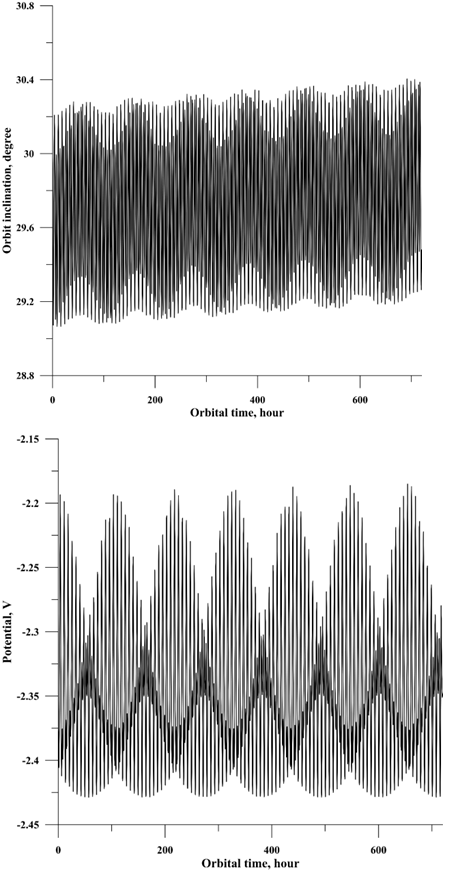
Figure 9 & 10 Dependences of the inclination of the orbit (9) and the electric potential (10) of the micro-particle with non-equilibrium electric charges on time injected with an initial inclination of 30 degrees for the case of only 2 forces: the gravitational and the Lorentz force component due to the co-rotation field (without accounting for shading).

Received in,¹⁸ the results allow us to compare the evolution of the semimajor axis and eccentricity under the injection conditions indicated above (Figures 6–10) for two methods of calculation: 1) only two forces: the central Newtonian gravitational force and the magnetic component of the Lorentz force act on a granule whose electric charge is assumed locally equilibrium at each step of the numerical integration of the system of equations of motion of the granule; 2) a complete system of seven forces acts on the granule and numerically integrates a single system of equations of motion and charging the micro-particle.

The complete system of forces includes the central gravitational force, its perturbation caused by the Earth's polar compression, the magnetic component of the Lorentz force, the electric component of the Lorentz force, caused by the electric fields of co-rotation and convection, the solar pressure force and the resistance force of the neutral component of the atmosphere. It is shown that the existing differences are small. Thus, the influence of not only the co-rotation field but all other forces in addition to the Lorentz force due to the interaction of the MP charge with the dipole magnetic field of the Earth does not lead to a significant change in the behavior of the orbital parameters at sufficiently large time intervals (in comparison with the case the actions of only two forces).

Thus, for the micro-particles considered, in contrast to the magnetic field, the electric field of co-rotation causes slow changes in the basic parameters of the orbit. These changes consist of two components: monotonous growth of the mean values ​​of the semi major axis, eccentricity and angle of inclination, and their oscillations at a nonzero initial inclination angle with a period much greater than the period of the orbital motion. At sufficiently large time intervals (of the order of one month), the co-rotation field does not lead to a significant change in orbital parameters, but for even longer times these changes can become significant.

None.

Authors declare there is no conflict of interest.

1. Horanyi M, Houpis HLF, Mendis DA. Charged Dust in the Earth's Magnetosphere. Astrophysics and Space Science. 1988;144(1–4):215–229.
2. Kolesnikov EK, Chernov SV, Yakovlev AB. Lifetime of Microparticles in a Geosynchronous Orbit. Cosmic Research. 1999;37(4):446–448.
3. Merzlyakov EG. On the Motion of Submicron Particles in the Low Near-Earth Orbits. Cosmic Research. 1996;34(5):558–560.
4. Kolesnikov EK, Chernov SV. Microparticle Residence Time in Low Near-Earth Circular Orbits. Cosmic Research. 1997;35(2):221–222.
5. Kolesnikov EK. Peculiarities of the Orbital Motion of Submicron Particles in the Earth's Plasmasphere. Cosmic Research. 2001;39(1):92–97.
6. Kolesnikov EK, Chernov SV. Dimensions of Microparticles Trapped by the Earth's Magnetic Field at Various Geomagnetic Activity Levels. Cosmic Research. 2003;41(5):558–560.
7. Kolesnikov EK, Chernov SV, Yakovlev A. On Correctness of Canonical Formulation of the Problem of Motion of Submicron Particles in the Earth's Plasmasphere. Cosmic Research. 2007;45(6):471–475.
8. Arnold VI. A proof of the Kolmogorov's theorem on the conservation of conditionally-periodic motions at a small change of the Hamilton function. Uspekhi Matematicheskikh Nauk. 1961;25(1):21–86.
9. Moser Yu. Some aspects of integrable Hamiltonian systems. Uspekhi Matematicheskikh Nauk. 1981;36(5):109–151.
10. Yakovlev AB. About the stability of the motion of microparticles of space debris of the Earth's plasmasphere. Sixth European Conference on Space Debris. Abstract Book. ESA, France, 2013. p. 121.
11. Kolesnikov EK, Yakovlev AB. On preservation of the form of the orbit of a microparticle with a variable charge moving in the Earth plasmasphere. Bulletin of St. Petersburg State University, Russia, 2014. p. 116–123.
12. Goldstein H. Classical Mechanics. Cambridge (Mass.): Addison-Wesley, USA. 1953.
13. Hill JR, Wipple EC. Charging of Large Structures in Space with Application to the Solar Sail Spacecraft. Journal of Spacecraft and Rockets. 1985;22:245–253.
14. Kolesnikov EK, Chernov SV. Development of methods for numerical simulation of the dynamics of fine-dispersed particles in near-Earth space. Models of continuum mechanics. Review reports and lectures of the 17th session of the International School on Models of Continuum Mechanics, Kazan, Russia, 2004. p. 55–83.
15. Dorman LI, Smirnov VS, Tjasto MI. Cosmic rays in the Earth's magnetic field. Nauka, Russia. 1971.
16. Braun M. Particle Motion in a Magnetic Field. Journal of Differential Equations. 1970;8(2):294–332.
17. Duboshin GN. Celestial mechanics, Main tasks and methods. Nauka, Russia. 1964.
18. Yakovlev AB, Kolesnikov EK, Chernov SV. Analytical research on the possibility of the long orbital existence of submicron particles in the Earth's plasmasphere by the methods of the KAM theory. Journal of Plasma Physics. 2017;83(4):1–17.