Electromagnetic waves can give us information about certain situations, but the loss of energy due to contact or penetration into surfaces can vary the information data when it is influenced by the relative permittivity of the medium and the dielectric constant of some materials, so for the detection, it is necessary to investigate other types of signals that do not generate loss of information, when they are used for detection in terrains with particular characteristics. In this research, the detection capacity of a GPR system is analyzed when it makes use of wavelet-type signals, which are better known as a signal analysis tool, resulting in wavelet-type signals that can identify buried objects when transmitted. and received under the amplitude analysis, the correlation and the penetration depth of the signal.

Keywords: signals wavelets, correlation, GPR

Ground Penetrating Radar) can be used. Various investigations have allowed the GPR to be used in applications such as the structural analysis of civil works in tasks such as mapping the deterioration of a subway infrastructure¹ or the detection of cavities or tunnels;^2,3 In archaeology, for example, it has been used in the characterization of Roman ruins;⁴ in geology for the determination of land characteristics;⁵ for search and rescue in catastrophes⁶ and in the search for anti-personnel mines.⁷ To carry out this work, the GPR is supported by the principle of propagation of electromagnetic waves through the phenomena of refraction, reflection and diffraction of these in a discontinuous medium. It is important to note that the waves used are in the VHF (Very High Frequency) and UHF (Ultra High Frequency) bands, which means that their application is neither destructive nor invasive of the medium where they propagate.⁸

Since the main application of the GPR is the detection of objects, holes or changes in the characteristics of the materials, to obtain good results it is important to take into account: the effects of the environment on the signals, the noise levels (of instruments or external)⁹ and the losses or attenuations of the system.⁸ As in a conventional radar, in the process of locating buried objects in different scenarios, the GPR mainly uses sinusoidal waves, either continuous or pulsating, with constant amplitude and frequency or constant amplitude and variable frequency, always looking for the best resolution. in the detection of objects trying to reduce to a minimum percentage the loss of energy when detecting and identifying buried objects. Considering that the main properties of the wave field are propagation speed, attenuation and electromagnetic impedance, it is easier to mathematically express the effects of the medium (permittivity, permeability and conductivity) if the wave is sinusoidal.¹⁰ However, taking into account the advances in electronic devices, as well as the current high capacities for both data processing and signal processing, it is important to consider these advantages when working with other types of waves or signals to analyze their behavior with a view to improving the detection capabilities of a GPR system.

The ground conditions must be taken into account (if it is flat or has roughness, or if it is dry or humid, for example) since depending on the frequency of the signal, the detection of a buried object is affected. Dry materials, such as sand, clay or stones, have the advantage of having a higher density of molecules per unit volume, this implies that there is less space to be filled with water or air molecules, generating a terrain with a smaller relative permittivity, which translates into a greater range in penetration since the attenuation is lower when entering the terrain.¹⁰ For this reason, a dry clay soil is chosen to evaluate the performance of wavelets in a GPR system. In this context, the present investigation will specifically address the use of wavelet-type waves in a GPR system with frequencies suitable for a medium such as dry clayey soil, seeking to know their behavior.

The Ground Penetration Radar (GPR) makes use of the propagation of electromagnetic waves, so its fundamental bases are in electromagnetic theory. Electromagnetic fields are described mathematically by Maxwell's equations, which combined with relations or constitutive equations, which quantify the properties of materials, give support to describe GPR signals quantitatively.¹⁰ Many scientists throughout the 19^th century worked on four laws that relate electric and magnetic fields to the currents and charges that generate them; however, it was James Clerk Maxwell who brought together these experimental works and determined that with only four equations or laws electromagnetism is fully described.¹¹ Maxwell's equations that relate electromagnetic fields are expressed as follows:

$\nabla \cdot \overrightarrow{D}=\rho$ (Gauss's law for electric field) (2.1)

$\nabla \cdot \overrightarrow{D}=0$ (Gauss's law for the magnetic field) (2.2)

$\nabla X\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}$  (Faraday's Law) (2.3)

$\nabla x\overrightarrow{H}=\overrightarrow{J}+-\frac{\partial \overrightarrow{D}}{\partial t}$ (Generalized Ampere's law) (2.4)

where,

1. $\overrightarrow{E}$ : electric field intensity (v/m),
2. $\rho$ : electric charge density ($c/m^3$ ),
3. $\overrightarrow{B}$ : magnetic flux density (T),
4. $\overrightarrow{J}$ : electric current flux density (A/m²),
5. $\overrightarrow{D}$ : displacement vector (c/m²),
6. t: time (s),
7. $\overrightarrow{H}$ : magnetic field intensity (A/m).

To describe how a material responds to electromagnetic fields, the constitutive relationships or equations are used, since these describe how electrons, atoms and molecules respond to the application of an electromagnetic field, these equations are:¹⁰

$\overrightarrow{J}=\sigma \overrightarrow{E}$  (2.5)

$\overrightarrow{D}=\epsilon \overrightarrow{E}$  (2.6)

$\overrightarrow{B}=\mu \overrightarrow{H}$  (2.7)

This system of equations contains the three parameters that characterize a medium electromagnetically: conductivity σ, permittivity ε and permeability μ. In the presence of an electric field, the conductivity σ characterizes the movement of free charge and therefore the conductive properties of the material. The dielectric permittivity ε of a material indicates how much it is affected by an electric field, providing a measure of the polarization capacity of a material in the presence of an electric field. The relative permittivity term (ε_r) _{or dielectric} constant is often used, which is defined as:

${\epsilon }_r=\frac{\epsilon }{{\epsilon }_0},$  (2.8)

where ε₀ is the permittivity of the vacuum (8.89 x 10 ^-12 F/m). Finally, the magnetic permeability μ indicates how the atomic and molecular moments of the material respond to a magnetic field.¹⁰

As can be seen, the constitutive equations relate the intensity of the electric field with the electric displacement and the intensity of the magnetic field with the magnetic induction. For homogeneous, isotropic, linear, nondispersive, and nonmagnetic media, the dielectric permittivity 𝜀 , the conductivity of the medium 𝜎, and the magnetic permeability 𝜇 of the material are constant; On the other hand, if the material is dispersive, they must be expressed as complex functions of the frequency and the position vector.¹³ This shows that 𝜀, 𝜎 and 𝜇 are tensor quantities that may not be linear, however, for practicality these quantities are considered independent of the fields and are treated as scalars, with 𝜀, and 𝜎 being the most important for GPRs, since 𝜇 is not of much concern for these systems. On the other hand, materials with low conductivity (𝜎 →0) would allow the GPR to reach great depths, although these conditions are not frequent.¹⁰ According to Jol.¹⁰ for a GPR in the frequency range between 10Mhz to 1000Mhz, the compounds and minerals in the mixtures have a permittivity between 3 and 8, which can present almost zero conductivity.

The operation of the GPR is based on the detection of reflections or dispersions of the emitted signals. When the emitted energy reaches a discontinuity in the electromagnetic parameters of the medium, reflection and refraction phenomena occur. This is related to the change in the direction of travel of the signal (ie, the wavefront is refracted), in accordance with Snell's law.¹⁰ Figure 1 schematically presents the aforementioned Reflection and Refraction phenomena of energy.

Figure 1 Reflection and refraction of a wave in two media with different characteristics.¹²

Snell's law relates the angles of incidence, reflection and refraction to the propagation speed of the signal or the permittivity of the media. In the GPR system due to the fact that the transmitted signal changes between two media such as between air (ε_r,air =1) and earth (ε_r,earth =4) it is established that the equation that describes the system is:⁸

$sen \alpha =\sqrt{{\epsilon }_{r,tierra}}*sen \theta$  (2.9)

A wave is reflected when the incident wave meets a change in the material and the angle of reflection is the same as the angle of incidence, taking as reference the perpendicular to the surface. On the other hand, the change in direction of the signal occurs when it passes from one medium to another with a different refractive index, with an angle of incidence other than zero degrees with respect to the normal of the surface. As the GPR system depends on the energy received by the receiving antenna, it is important to take into account that this energy comes from the energy that is reflected by each discontinuity in the medium, the reflection coefficient being the percentage of the reflected energy.⁹ According to Bustamante (2015), the impedance of an electromagnetic field is the quotient between the electric field $\overrightarrow{E}$ and the magnetic field $\overrightarrow{H}$ , being able to define an impedance for the incident electromagnetic field in air, which is equal to that of the reflected magnetic field, and another for the refracted electromagnetic field, n ₂ :⁹

$n_{aire}=\frac{\overrightarrow{E_{{}_l}}}{\overrightarrow{H_l}}=\sqrt{\frac{{\mu }_0{\mu }_{r,aire}}{{\epsilon }_0{\epsilon }_{r,aire}}}$  (2.10)

$n_{tierra}=\frac{\overrightarrow{E_t}}{\overrightarrow{H_t}}=\sqrt{\frac{{\mu }_0{\mu }_{r,tierra}}{{\epsilon }_0{\epsilon }_{r,tierra}}}$ (2.11)

The expressions of the impedances can be calculated knowing the Fresnel coefficients of the energy in transmission (T) and reflection (R), according to equations (2.12 and 2.13) as a quotient of the refracted field (transmitted) and the incident field (reflected) in a first situation, and in a second situation as the quotient between the reflected field and the incident field. If ${\theta }_i$ is the angle of incidence of the wave on the flat surface, and ${\theta }_t$ is the angle of refraction, the coefficients under the parameters of the angle of incidence and refracted are defined mathematically as follows:⁸

$\perp R_{aire-tierra}=\frac{\overrightarrow{E_r}}{\overrightarrow{E_l}}=\frac{n_{tierra}\cos ({\theta }_t)-n_{aire}\cos ({\theta }_i)}{n_{{}_{aire}}\cos ({\theta }_i)+n_{tierra}\cos ({\theta }_t)}$   (2.12)

$\perp T_{aire-tierra}=\frac{\overrightarrow{E_{{}_t}}}{\overrightarrow{E_l}}=\frac{2n_{tierra}\cos ({\theta }_t)}{n_{{}_{aire}}\cos ({\theta }_i)+n_{tierra}\cos ({\theta }_t)}$

where T (Transmission) _air--ground is the Fresnel coefficient of refraction between air and dry clay soil, and R (Reflection) _air--ground is the Fresnel coefficient of reflection for the two media,${\overrightarrow{E}}_l$ is the incident field,${\overrightarrow{E}}_r$ the reflected field and ${\overrightarrow{E}}_t$  the refracted or transmitted field in the other medium. For the case of waves parallel to the medium, the coefficients are given by:

$\parallel R_{aire-tierra}=\frac{\overrightarrow{E_r}}{\overrightarrow{E_l}}=\frac{n_{tierra}\cos ({\theta }_i)-n_{aire}\cos ({\theta }_t)}{n_{tierra}\cos ({\theta }_i)+n_{aire}\cos ({\theta }_t)}$ (2.13)

$\parallel T_{aire-tierra}=\frac{\overrightarrow{E_{{}_t}}}{\overrightarrow{E_l}}=\frac{2n_{aire}\cos ({\theta }_t)}{n_{tierra}\cos ({\theta }_i)+n_{aire}\cos ({\theta }_t)}$

In the event that the reflecting surface is flat, for the GPR the mathematical expressions of the previous equations can be simplified since the system operates with a very small angle in its reflection effect, and the angles of incidence and reflection can be considered equal. Under these conditions, the reflection and transmission coefficients will only depend on the relationship between impedances. However, if working in non-magnetic media, an adequate approximation for most of the materials in which these studies with GPR are applied, the expression of the coefficients can be reduced to the following mathematical expressions:

$R_{aire-tierra}=\frac{n_{{}_{aire}}-n_{tierra}}{n_{{}_{aire}}+n_{tierra}}=\frac{\sqrt{{\epsilon }_{r,aire}}-\sqrt{{\epsilon }_{r,tierra}}}{\sqrt{{\epsilon }_{r,aire}}+\sqrt{{\epsilon }_{r,tierra}}}$  (2.14)

$T_{aire-tierra}=\frac{2n_{aire}}{n_{{}_{aire}}+n_{tierra}}=\frac{2\sqrt{{\epsilon }_{r,aire}}}{\sqrt{{\epsilon }_{r,aire}}+\sqrt{{\epsilon }_{r,tierra}}}$ (2.15)

Something characteristic of the previous mathematical equations is that the sum of the percentage of energy reflected within the reflection coefficient and the percentage of incident energy of the refraction coefficient results in unity. Therefore, it can be deduced that the greater the difference between the electromagnetic parameters of the media, the greater the reflection coefficient will be, which generates a higher percentage of reflected energy at the border of the two media and therefore will have a lower percentage. of transmitted energy for dry clay soil, this will not allow the remaining energy to interact in a greater percentage at the time of locating the object since it was dispersed by reflection effects on the surface. High values of energy in Reflection in the medium imply in the GPR the possibility of obtaining records of the reflected wave with very low resolution and the reflections produced at the moment of locating the object have lower amplitudes due to the effects of refracted energy, which As a consequence, the amplitude of the wave in reflections will be lower when it interacts with the object to be located.^9,10,13

Wavelet signals

At an academic level, the mathematical model called wavelet transform has been used for signal analysis, and this is how it has been used both in radar and GPR applications, normally seeking to improve the information received by removing noise,¹⁴ interference or recognizing objects. On the other hand, there are few works where the use of wavelets waves as a signal to be transmitted in radars has been addressed.^15–17 According to Kaiser G (1996), wavelets are two-way waves, initially seen as localized acoustic or electromagnetic waves¹⁸ and later as functions that are related by displacement and scale and that form a base (or frame). for a vector space of functions (Morlet, Grossman, Meyer, Daubechies among others).¹⁹ A wavelet $\psi (t)$ is a wave form of finite or limited duration, which must have zero mean value, finite energy and meet an admissibility condition, which can be expressed mathematically as:²⁰

${\displaystyle {\int }_{-\infty }^{\infty }\psi (t)dt=0}$ (2.29)

${{\displaystyle {\int }_{-\infty }^{\infty }\left|\psi (t)\right|}}^{2}dt<\infty$ (2.30)

${{\displaystyle {\int }_{-\infty }^{\infty }\left|\psi \left(\omega \right)\right|}}^2\frac{d\omega }{\left|\omega \right|}<\infty$  (2.31)

where $\psi \left(\omega \right)$ is the Fourier transform of $\psi \left(t\right)$ . The admissibility condition (2.31) implies that the wavelet function, when used as a transform, is invertible.¹⁵

Two basic transformations can be applied to a base function (mother wavelet):

1. Change of scale: by means of a parameter it is compressed or dilated$\psi \left(t\right)$
2. Translation: moves $\psi \left(t\right)$ in time using a parameter $b$

Thus creating a given wavelet family defined by:

${\psi }_{ab}(t)={\left|a\right|}^{-\frac{1}{2}}\psi \left(\frac{t-b}{a}\right).$  (2.32)

Waveguide antenna design

For the development of this research, it was necessary to manufacture a directed waveguide antenna with a dipole inside, the online software waveguide (2015) was used, which provides the different design specifications such as wavelength, dipole measurements. and frequency range of the antenna. The program requires the diameter of the antenna which is 7.6 cm and will deliver the specific data for the construction. Channel 1 was selected to avoid losses that could be generated by signal dispersion multipath effects, according to the manufacturers' instructions. The central frequency of this channel (2.412Ghz) is in accordance with the working range of the USRPB210 which is between 70 MHz and 6 GHz. Thus, the data obtained according to the specifications were the diameter of some known tubes and the frequency established by the USRP at the time of making the transmission:

Diameter: 3".

Frequency: 2.81GHz.

Where the software gave the following results;

Wavelength in free space: 0.1067 m

Minimum frequency: 2.465 GHz

Maximum Frequency: 2,817 GHz

Cutoff Frequency: 2.313 GHz

Dipole length: 2.67 cm

Waveguide antenna design software

For the antennas, an online software was used that allows the construction of a waveguide using a cylinder, called Building the cylinder (Can) Waveguide.²¹ This gives the values of the dipole measurement and different specifications to take into account in the construction, we can see it in Figure 2.

Figure 2 Data obtained by the software for the manufacture of waveguide antennas.

Matlab integration – GNU Radio

Using Matlab, the signals are generated, which are saved in the files on the computer. Then the stored file corresponding to the signal to be transmitted is loaded by GNU radio for transmission through the USRPB210. Then it goes through the object that is buried and the information obtained is stored to deliver it again to Matlab for the respective processing. The wavelet signal to be transmitted is initially generated in Matlab® from its mathematical equations, which is received by the GNU Radio software through a file. In the same way, the information received by GNU Radio (reflected signal) is delivered in a file to Matlab for further analysis. To facilitate the selection of the wavelet wave, define its conditions and generate the base signal to be transmitted, the Matlab Guide application was used, whose graphic format facilitates interaction with the user. Figure 3 shows the designed interface.

Figure 3 MATLAB graphical interface, for wavelet wave selection.

In the case of the Matlab® graphic interface, there are three sections:

Section 1: Loading the waves to be transmitted (by means of ordering buttons) (red box).

Section 2: Graphs of the transmitted and received waves for processing (by visualization of graphs) (Green box).

Section 3: Storage of the different data in relation to depth calculations (through the boxes that provide the information in numerical form) (Blue box).

In the part where section 3 is found. In the blue box are the buttons for storing the different data at different depths between the values of 1 cm to 6 cm. And in the lower left corner of the image the specifications of the antenna design. All this in order to constantly monitor the transmitted signal and the received signal to keep in mind the changes that can be generated in relation to the depth of penetration.

GNU radio - USRP

GNU Radio is the software in charge of programming the USRP B210, and it is programmed according to the conditions indicated by the user. One of the great advantages of GNU Radio is that it is programmed by connecting dedicated, communications-oriented blocks. The exchange of information (programming and signal data) is done through a USB connection between the computer and the USRP. The union of the entire system is observed in Figure 4. Where it is observed that the exchange of information between Matlab and GNU Radio is through storage files in some folders which, through function blocks, are passed to GNU radio which at each stage does the corresponding thing. So that the signal can be transmitted.

Figure 4 Stages of the implemented GPR system.

Transmission process:

Stage 1: Loading the file that has the information of the wave to be transmitted

Stage 2: Conditioning of the signal to be transmitted in this case the real part

Stage 3: Frequency adjustment of the signal to be transmitted for object location

Reception process:

Stage 1: Data verification after having passed through the object

Stage 2: Delivery of real part data to Matlab

Stage 3: Storing data after having passed through the object.

The connections through blocks of the different components that will allow the transmission of the selected waves through the Tx and Rx ports. The SMA cable is a type of coaxial cable with thin, small-diameter threaded connectors to be adjusted in the different transmission and reception ports. The USRP has a cable with a USB connector which connects to the 3.0 port of a laptop for its implementation (Figure 5).

Figure 5 Physical connection diagram with the USRP B210 card of the transmitter system.⁸

Experimental GPR system

The implementation of the GPR system is carried out in the following stages:

Stage 1: The Assembly of the GPR is carried out, whose implementation of the experimental system can be seen in Figure 6 & 7 where the interior of the antenna is observed.

Figure 6 a) Assembly of the experimental GPR system b) Measurements of the experimental assembly.

Figure 7 Antenna observed from inside with its dipole.

Stage 2: Creation of the Matlab programs that allow the generation of each of the wavelets and their storage in a folder named ondas_MATLAB.

Stage 3: Implementation of the transmission-reception system in GNU Radio. The implemented block diagram can be seen in Figure 8.

Figure 8 Diagram of transmitter and receiver in GNU Radio.

The blocks used GNU Radio:

Control blocks

QT GUI RANGE: Allows adjustment in a determined range with accompaniment in the graphical interface

QT TAB WIDGET: Allows you to place a frame for the wavelets, terrain scanner and frequency tabs for user selection.

QT CHECK BOX: Allows you to document the GNU radio interface.

QT WATERFALL SINK: Allows observing the detection from another panorama.

QT GUI FREQUENCY SINK: Register the frequency

OPTIONS: Allows you to give author characteristics, software characteristics and its description.

VARIABLE: Allows the adjustment of local variables to be worked on in the execution blocks, in this case the frequency.

Execution blocks

FILE SOURCE: It is where the file delivered by MATLAB is loaded. for the respective broadcast.

RATIONAL RESAMPLER: Which is a block that multiplies by a factor (interpolation/decimation) the frequency that arrives to be adjusted or coupled.

UHD USRP SINK: Adjusts the signal to a known channel frequency to be transmitted (2.81 GHz)

UHD USRP SOURCE: Allows you to receive the signal using a preset frequency.

FLOAT TO COMPLEX: The real part of the signal generated by MATLAB is taken, canceling the imaginary part.

AUDIO SINK: Generates an audio file.

FILE SINK: Saving the .dat extension file for later analysis.

GNU Radio additionally offers user interface blocks where the signals delivered by the blocks can be monitored. Figure 9 shows an example of the transmitted signal and the received signal in an experiment.

Figure 9 Graph delivered by GNU Radio of the signal transmitted and the signal received.

Stage 4. GNU radio stores the reception information in a .dat file in a folder called GNU radio data which can be later loaded by MATLAB for analysis.

In order to know the performance of the implemented system, the following experiences were carried out:

1. Experience 1. Characterization of waveguide antenna. The base band band width, the silence period and the radiation pattern are obtained.
2. Experience 2. Determination of the operating conditions of the waveguide obtained by the online software.
3. Experience 3. Transmission of a wavelet wave adjusting the angle of the transmitting antenna for values of 45º, 48º, 51º, 54º, 57º and 60º.
4. Experience 4. Determination of the angle of greatest possible radiation, adjusting the angle at 45°, 50° and 60°.
5. Experience 5. Discrimination of two objects by varying the separation distance between them from 1-5 cm.
6. Experience 6. Behavior of waves when the object is introduced on the ground at a frequency of 2.81 GHz

Each of the experiences is described using the following items:

1. Experience name
2. What do you look for with experience?
3. Conditions
4. Results obtained.

This is how they were developed:

Experimentation of the GPR through 5 research experiences: determination of the operating conditions; experimental determination of the best transmission angle, observation of the discrimination area and the behavior of each of the waves when gaining levels of depth.

Experience 1

Characterization of the waveguide antenna

What do you look for with experience?

Experimentally verify the correct transmission of the wave and obtain its radiation pattern, its bandwidth.

Conditions

1. 1m separation distance between two antennas, one with characteristics known by the manufacturer (log periodic antenna) and a manufactured waveguide.
2. Transmission power of 0.05 W
3. Signal generator frequency: 900.297 MHz
4. Known 5 dB log periodic antenna gain

Results obtained

In the signal laboratory, a transmission was carried out between two antennas, the constructed waveguide and the periodic log. Under the known conditions of the gain of the log-periodic antenna of 5dB and the wavelength λ = 0.33 m, a distance r=1 m was transmitted with a power in the generator of 0.05 Watt, to know the gain of the waveguide (GR) under equation (2.39), was carried out as follows, it began to transmit at different frequencies from 5000Hz to 5000Hz by the log periodic antenna and as a receiver the waveguide the results can be evidenced in Table 1. Clearing the equation (2.39) GR it was possible to obtain the value of the gain of the waveguide antenna whose value was 3.29 dB.

Through observations in the telecommunications laboratory equipment, the response of the antennas in the signal spectrum analyzer was determined, the transmission and reception were verified in the circular platform of the signal laboratory, as can be seen in Figure 11–14 and the directivity of the waveguide which showed the radiation pattern that can be seen in Figure 13, taken at a distance of 38 cm, which is the working distance of the system test bench, as a basis for demonstrate the behavior of the manufactured antenna. This experience also allowed to determine the bandwidth of the transmitted signal, this was obtained by using the reference spectrum analyzer HP8590A. For this, a pulse was sent and with the spectrum analyzer it was determined that the bandwidth is 30 KHz as can be seen in Figure 10. Figure 1 Received signal spectrum analyzer transmission and reception verification as observation of signal bandwidth where the value of 30 KHz can be seen. Figure 14 shows the behavior of the signal transmission at a frequency of 2.81 GHz within an impedance of 52.296 Ω which verifies that the antenna is working optimally within the frequency established for its transmission.

Figure 10 Bandwidth obtained experimentally. (Own elaboration)

Figure 11 Stability in the error of each of the signals. (Own elaboration)

Figure 12 Platform for obtaining the radiation pattern, frontal and lateral view.

Figure 13 Waveguide antenna radiation pattern.

Figure 14 Response of the antenna at a frequency of 2.8Ghz.

For the bandwidth of the baseband signal according to Figure 10, the radio frequency signal with BW bandwidth is captured by the antenna and taken to the card according to the work specifications of the USRPB210 whose width The bandwidth is up to 56 MHz. Experimentally under the spectrum analyzer the bandwidth of the transmitted signal is 30KHz (Figure 15). The desired band enters the Mother board where it is amplified again, it is digitized at 61.4 million samples per second (MS/s) as the¹ maximum possible sampling frequency worked by the USRP according to the analog-digital conversion established internally, and thanks to the NCO (Numerical Controlled Oscillator) the frequency deviation is eliminated obtaining the baseband signal, finally a decimation by N is performed, so the sample rate that will be sent through the USB interface will be 64 MS/s /N.^8,22

Figure 15 Block diagram in the process of obtaining the signal.⁸

Experience 2

Determination of the operating conditions of the waveguide obtained by the online software.

What do you look for with experience?

Experimentally verify the correct transmission of the wave and obtain the transmission power.

Conditions

1. Diameter of the metallic cylinder used to manufacture the antenna; 7.6 cm.
2. Wave length inside guide 10.7 cm
3. Online software for antenna design.
4. Displaced reflective sheet used as antenna reflector

Results obtained

Using the software ( https://www.wikarekare.org/Antenna/WaveguideCan.html ) (Figure 9) the corresponding data was inserted, which allowed obtaining the following results:

Frequency to transmit: 2.81 GHz

Dipole length: 3cm

Antenna length: 31.58 cm

Distance from dipole to reflective part: 7.9 cm

Distance from dipole to front of antenna: 15.79

With these data we proceeded to build the antenna.

Subsequently, taking as reference Figure 6 b). Where the measurements of the test bench named below are specified:

From dipole to ground surface Dd=0.29 m

Of the buried object with respect to the surface Do=0.06 m,

From the dipole to the edge of the antenna Da=0.1579 my

Morlet wavelet transmitted wave.

The transmission and reception of a wave was verified experimentally to be later implemented through the GNU radio software for its respective transmission and reception.

Step 1: Adjust the distance between the two antennas to 40 cm since the test bench will work in this distance range Figure 16.

Figure 16 Alignment of antennas for transmission test. (Own elaboration)

Step 2: Transmission of a wavelet wave for observation through the oscilloscope if it is being transmitted or not Figure 17.

Figure 17 USRP AND PC connection. (Own elaboration)

Step 3: Take the peak to peak voltage of the obtained signal. Where in the oscilloscope of the signal laboratory you can clearly see the voltage of 23.5 mv of the Morlet signal (inverted) Figure 18.

Figure 18 Wavelets signal recognition test on an oscilloscope. (Own elaboration)

Results obtained

The correct transmission and reception of the signal (Morlet wave) was verified with a peak-to-peak voltage of 23.1 mV and it was determined that the antenna gain is 0.0032 dBm. These results were obtained in the laboratory for a distance of 37.5 cm between the two antennas.

Experience 3

Transmission of a wavelet wave adjusting the angle of the transmitting antenna ${\theta }_1$ for values of 45º, 48º, 51º, 54º, 57º and 60º.

What do you look for with experience?

This experience is carried out in order to verify how much the measurements taken in the detection and position of an object vary, through the use of the experimental GPR device, with respect to the expected real location. The results obtained are a step to determine what must be adjusted in the GPR system or what conditions must be taken into account for it to operate properly.

Conditions

In the experiments carried out, taking as reference Figure 6 a). The fixed measures of the system correspond to the distances:

1. From dipole to ground surface Dd=0.29 m
2. Of the buried object with respect to the surface Do=0.06 m,
3. From the dipole to the edge of the antenna Da=0.1579 m and the transmitted wave was the Gaussian wavelet.

Results obtained

For the experimental measurement of the buried object, the distance measurement between samples of the autocorrelation of the transmitted signal and the cross-correlation between the transmitted and the received signal is used, for which 15 experiences were made for each one of the defined degrees. for the frequencies of 2.5 GHz and 2.81 GHz. For these experiments the real distance is D is adjusted depending on the angle of incidence. Table 2 & 3 shows the values at a frequency of 2.5 GHz. Figure 19 shows an example of the signals and correlation measurements for a 60º experience Table 4. Where it can be observed that for the angle of 45° and 60° there is a closer approximation in relation to the theoretical and experimental value.

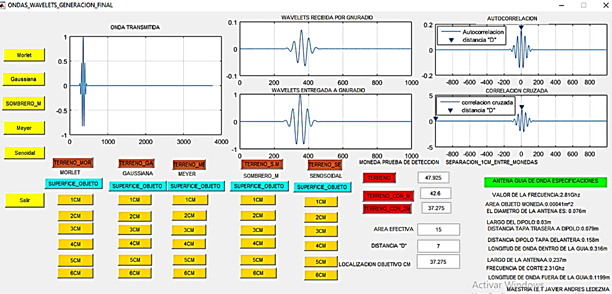
Figure 19 Transmitted, received, auto-correlation and cross-correlation waveform graph for an angle of 60º between the antennas with a transmission frequency of 2.81 GHz.

Experience 4

Determination of angle of greatest possible radiation, setting the angle ${\theta }_1$ at 45°, 50° and 60°

What do you look for with experience?

With this experience, by varying the reception and transmission angles of the antennas, the aim is to find at which angle the best possible energy radiation is obtained.

Conditions

Conditions of the experience:

In the experiments carried out, taking as reference Figure 6 a). The fixed measures of the system correspond to the distances:

1. From dipole to ground surface Dd=0.29 m
2. Of the buried object with respect to the surface Do=0.06 m,
3. From the dipole to the edge of the antenna Da=0.1579 m and the transmitted wave was the Gaussian wavelet.

From the reflection coefficients for perpendicular and parallel polarization, equations (2.12) and (2.13) respectively, the total reflection coefficient R _1-2 (total)=2(R _1-2 +||R _{1- 2}).

Results obtained

Table 5 shows the results obtained for this experience, where it can be seen that the lowest loss of reflection power is obtained for an angle ${\theta }_1=60°$ , and therefore this is the angle selected for the rest of the experiences.

According to the information in Table 5, which consists of taking three possible angles such as 45°, 50° and 60° as incident angles ϴi adjusted in the antenna to carry out the transmission and using Snell's law, calculate their respective angles. refracted under the surface called ϴt with these data then we proceed to make the records of the Fresnel coefficients that are calculated by means of equations (2.12 and 2.13) in order to obtain the values of the Fresnel coefficients, which allowed us to observe at the end of the calculations, between the attenuation data for each of the study angles, the value of -15.204 compared to the other two would be the lowest possible attenuation of the signal and therefore we could have for this corresponding value of 60° good concentration of energy when making transmissions compared to 45° and 50°.

Experience 5

Discrimination of two objects by varying the separation distance between them from 1 to 8 cm.

What is sought with experience

With this experience, we seek to determine what distance the system is capable of discriminating between two objects when they are separated from each other at a certain distance on clayey soil.

Conditions

1. Use two coins of equal diameter.
2. Separate them cm by cm.
3. Transmission frequency used: 2.81 GHz.

Results obtained

The procedure was carried out by separating two coins cm by cm in order to verify the coverage footprint of the antenna on the ground surface. When, when separating the coins, the amplitude value measured by the system takes values similar to as if there were no coins on the surface, it indicates the discrimination capacity of the system, that is, the distance that must exist between the two coins for it to can identify them independently. Through the interface made in the Matlab guide, the data is taken, which can be seen in Table 6. This table shows the amplitudes received as the coins are separated cm by cm.

According to this information, the system is capable of discriminating coins that are separated by more than 8 cm, since as they separate, the value of the amplitude measured at reception decreases, as can be seen in Figure 21, and it is from 8 cm apart where the amplitude level measured in the receiver is approximately equal to the value measured without coins. Now, since the material used is a coin with a diameter of 2.3 cm (with an area a equal to $A=\pi *r^2=$ 3.1416. (1.15cm) ² =4.15 cm ²), then as the coins move away, the angle The incidence is adjusted and the reflection area also decreases, causing the reflection coefficient to become less and less and therefore the signal received by the antenna is of lesser amplitude. Coming to observe in Figure 20, that at a separation distance of 4cm between the coins a 50% loss of amplitude is obtained, which indicates that the system is not capable of discriminating the existence of two coins, which occurs only from at least 8 cm distance between them.

Figure 20 Amplitude of the receiver in relation to the separation of the coins.

Figure 21 Comparison of wavelets at different penetrations. (Own elaboration)

Experience 6

Wave behavior when the object is introduced into the ground at a frequency of 2.81 GHz

What is sought with experience

Determine which of the signals penetrates further into a depth established according to the 6 cm test bench in Figure 6 a & b).

Conditions

1. A coin AS A REFLECTIVE ELEMENT
2. Depths from 1 cm to 6 cm
3. 2.81GHz frequency
4. Transmission gain: 22 dB (According to equipment specifications)
5. Reception gain: 64 dB (According to equipment specifications)
6. Incident angle of 60°
7. From the dipole to the ground surface Dd=0.30 m
8. Of the buried object with respect to the surface Do=0.06 m,
9. From the end of the antenna to the surface Da=0.1535 m
10. Transmission of Morlet, Meyer, Gaussian, hat, sinusoidal pulse.

Results obtained

In Table 8. All the information of each one of the signals is stored when they are transmitted with GNU radio to carry out the calculation of the penetration depth experimentally, using equation 2.27 and the Matlab guide that can be seen in the Figure 21 (which, under the programmed internal correlation function, delivers the number of samples D of each of the transmission and reception signals with a period of 3.55x10^-10 s). For the theoretical distance column, the measurements were taken according to the design specifications of Figure 6 b), where, under Snell's law, the angle of refraction is obtained and with equation 2.9 of chapter 2, r2 is calculated, considered as the hypotenuse of the triangle that is formed under the surface, the value of r1 can be calculated under equation 2.41 of chapter 2 where Da according to the specifications of figure 8 is equal to 10.35 Cm and the angle ${\theta }_1=60$ .

Making use of equation 2.42, for r2=0 and since it is up to half, the value of the path of the theoretical beam on the surface is obtained:

Dist= (32cm +2*20.7)/2 =36.7cm

The level (0) is considered to be on the surface, the other theoretical measurements of the ray trajectory reported come from equation 2.9 but already with the angle of incidence (which is obtained by Snell's law that gives a value of = 25.46) ${\theta }_2$ .

The theoretical and experimental values of the distance traveled by the wave inside the dry land (r2) are recorded. The difference between the theoretical value and the one measured experimentally gives us the measurement error recorded in Table 8, this indicates the behavior of the signal in relation to the penetration into the terrain in terms of location of the object for each of the signals. Therefore, within the results obtained, it can be seen in Table 8 that the Morlet signal is the one that behaves best in relation to the location, presenting a constant error that shows its behavior well at the time of location until it reaches the level 5 where its depth is 5.47 cm, from there it is followed by the Meyer, Gaussian, Sombrero signal and finally the sinusoidal pulse. It was carried out in the following way, the object was introduced cm by cm on the dry clayey ground and transmissions of the signals were carried out one by one, on the ground. Each transmission generated a reception which was captured, this information on the location of the object within the dry clayey soil was stored in folders, to carry out the data processing under the formulas for calculating correlation and depth of the object using Matlab, as well The data was recorded for each of the signals and it was possible to observe that the wavelet signals as they gained depth up to the level between 5cm and 6cm still detected the depth of the object, when this value already began to have a constant behavior. it was deduced that up to that value the signal had reached its maximum detection Table 7. V éase la Figure 21  observe how the ódepth values changes nas waves penetrate.

Graphs of each of the waves at a frequency of 2.81 GHz

Figure 22 shows the penetration depth of each of the waves presented in Table 8 in relation to the surface and depth. As we can see in Figure 6. The Morlet wave reaches 5.47 cm at level 5 compared to the other waves. It is the one that penetrates the most in the dry clayey soil. According to Table 8, it can be seen that the signal that penetrated the most was the Morlet wave since its measurements did not vary in relation to its percentage error in the % Error column for level 5, showing a stable behavior until level 5, because between level 5 and 6 the signals present reflection and refraction effects with the final base of the tray, which means that their data is not very unstable, as can be seen in Figure 22, therefore up to level 5 cm are considered acceptable behaviors . According to the above, wavelet signals can be used to identify objects buried in dry clayey soil, as in this case, where the construction of a GPR system was implemented, for data collection of the different signals.

Figure 22 Stability in the error of each one of the signals. (Own elaboration)

¹The sample rate defines the speed with which the Analog/Digital converter takes the samples. (Spectrum instrumentation, 2023)

Wavelets can identify buried objects in their transmission and reception under signal correlation analysis and the depth equation used by GPR. When they penetrate the clayey soil, as can be seen in Figure 22, the wavelet signals have a lower error compared to a sinusoidal pulse for this case study, so they can be considered as signals to identify anomalies. Wavelet waves with symmetry characteristics can be implemented for the detection of buried objects or conducting terrestrial sounding, due to their ease of analysis as symmetrical finite pulses. The Morlet wave according to Figure 21 presents a good behavior at level 5, showing that it reached 5.47 cm compared to the other signals because its error percentage is lower. This investigation allowed us to verify that it is possible to design a GPR system using wavelet signals, considering that they are signals with finite energy and showing in the experimental results that wavelet signals present a better performance than sinusoidal for locating an object buried in dry land, therefore it is concluded that wavelet signals are a good option in a ground penetrating radar.

The transmission power of the USRP is low, so with a good directivity and gain of the antennas it is possible to supply power effects of the transmitter, to improve the transmission of the system they must be calibrated with an angle of 60° since this is how decreases the effects of attenuation between signals. The system implemented for this project is capable of locating objects at a depth of up to 6 cm, and this is important to highlight since antipersonnel mines can be buried at a maximum depth of 6 cm⁸ which is why the system may be suited to deliver more power to facilitate a deeper search.

None.

The author declares there is no conflict of interest.

1. Dawood T, Zhu Z, Zayed T. ‘Deterioration mapping in subway infrastructure using sensory data of GPR’. Tunnelling and Underground Space Technology. 2020;103:103487.
2. Feng X, Ren Q, Liu C. ‘Quantitative imaging for civil engineering by joint full waveform inversion of surface-based GPR and shallow seismic reflection data’. Construction and Building Materials. 2017;154:1173–1182.
3. Alsharahi G. ‘Detection of cavities and fragile areas by numerical methods and GPR application’. Journal of Applied Geophysics. 2019;164:225–236.
4. Zhao W. ‘GPR imaging and characterization of ancient Roman ruins in the Aquileia Archaeological Park, NE Italy’. Measurement. 2018;113:161–171.
5. Sonkamble S, Chandra S. ‘GPR for earth and environmental applications: Case studies from India’. Journal of Applied Geophysics. 2021;104422.
6. Diamanti N, Annan AP, Giannakis I. ‘Predicting GPR performance for buried victim search &amp; rescue’, in 2016 16th International Conference on Ground Penetrating Radar (GPR). IEEE, 2016. p. 1–6.
7. Ko KH, Gyubin Jang, Kyungmi Park, et al. 'GPR-based landmine detection and identification using multiple features'. International Journal of Antennas and Propagation. 2012.
8. Mendoza Patiño E de J. Programming of an sdr (software defined radio) platform for the detection of antipersonnel mines. Pontifical Javeriana University. 2014.
9. Ruiz Salazar J, Orejuela Caicedo DA. Implementation of the wavelet transform on an embedded system for the pre-processing of non-stationary one-dimensional signals. UNIVERSITY OF SAN BUENAVENTURA CALI. 2016.
10. Jara Bustamante CA, Valdebenito MG, Iroume AA. 'Geophysical exploration using the ground penetrating radar technique a state of knowledge'. 2015. p. 138.
11. Jol HM. Ground Penetrating Radar Theory and Applications. Elsevier. 2009.
12. Ayala Cabrera D. Characterization of buried pipelines for supply networks in service through the analysis of images obtained with subsoil radar (Ground Penetrating Radar - GPR). Department of hydraulic engineering and environment master's thesis. Polytechnic university of Valencia. 2009.
13. Van der Wielen A. Characterization of thin layers into concrete with Ground Penetrating Radar. University of Liège. 2014.
14. Javadi M, Ghasemzadeh H. 'Wavelet analysis for ground penetrating radar applications: A case study'. Journal of Geophysics and Engineering. 2017;14(5):1189–1202.
15. Kaiser G. ‘Physical wavelets and radar: a variational approach to remote sensing’. IEEE Antennas and Propagation Magazine. 1996;38(1):15–24.
16. Cao SY, Zheng YF. ‘Recent Developments in Radar Waveforms’. 2014. p. 3.
17. Cao S. Radar Sensing Based on Wavelets. Graduate Program in Electrical and Computer Engineering. Doctor of Philosophy in the Graduate School of The Ohio State University. 2014. p. 1–24.
18. Huygens D. 'Detecting, locating, and characterizing voids in disaster rubble for search and rescue'. Advanced Engineering Informatics. 2019;42:100974.
19. Saavedra-Gastélum V, Fernández-Harmony T, Harmony-Baillet T, et al. Wavelets in engineering: Principles and applications. Engineering, Research, and Technology. 2006;7(3):185–190.
20. Gómez-Luna E, Silva D, Aponte G. 'Selection of a mother wavelet for the frequency analysis of transient electrical signals using WPD'. Ingeniare. 2013;21(2):262–270.
21. Waveguide. Building the Cylinder (Can) Waveguide. 2015.
22. Spectrum instrumentation. Sample rate details. 2023.