In some molecules such as ammonia, double vibrations are observed at small energies. These small vibrations are thought to arise from double well potentials. To explain these small energy gaps, double potential wells are investigated, and complex calculations are made. Until recently, since the exact solution of the Schrödinger equation was not known, approximate solutions were always obtained. The exact solution of the Schrödinger equation is now known. In previous studies, a simple procedure for the general solution of the radial Schrödinger Equation has been found for spherical symmetric potentials without making any approximation. In this article, the Schrodinger equation was solved with this new solution method. It has been applied to the oscillations through a barrier tunneling potential for a particle in a central quadratic deformed potential well (double potential well). It is seen that there is no need to look for complex potentials to explain the double wells observed in small vibrations in ammonia and similar molecules, they were compared with experimentally measured energies. The results were found to be fully compatible. It has been seen that there can always be double well potentials at small energies for all molecules, atomic nuclei, and similar particles with angular momentum other than zero.

Keywords: central potentials, radial equation, spherical symmetric potential, oscillations through a barrier tunneling, double potential well, small vibrations

Although the radial Schrödinger Equation (SE) for some simple spherical symmetric potential is solved, an exact solution is not possible in complicated situations, and it must be then resorted to approximation methods. For the calculation of stationary states and energy eigenvalues, these methods include perturbation theory, the variational method and the WKB approximation. Perturbation theory is applicable if the Hamiltonian differs from an exactly solvable part by a small amount. The variational method gives a good estimate of the ground state energy if one has a qualitative idea of the form of the wave function and the WKB method is applicable in the nearly classical limit. In one of the previous studies, it has been achieved a simple method for the exact general solution of the radial SE for spherically symmetric potential well of any form without making any approximation. This simple solution method has been applied to many spherical symmetric potential.^1,2 In this study, we have applied this simple method to solve the oscillations through a barrier of potential (double potential well). It was applied to the ammonia molecule, and it was seen that the values calculated with experimental measurements agreed very well. It is seen that there is no need to look for complex potentials to explain the double wells observed in small vibrations in ammonia and similar molecules, and that there will be double wells in small vibrations in all molecules, atomic nuclei, and similar particles with non-zero angular momentum.

The SE in three dimensions is given as follows:

$\Delta \psi \left(\overrightarrow{r}\right)+\frac{2m}{{\hslash }^2} \left[E-V\left(\overrightarrow{r}\right)\right]\psi \left(\overrightarrow{r}\right)=0$   (1)

Where, E and V are the total and potential energies, respectively, m is the mass or reduced mass of particle. The spherical polar coordinates $\left(r,\theta ,\varphi \right)$ are given as follows:

$X=r sin\left(\theta \right) \cos \left(\varphi \right), y=r sin\left(\theta \right) sin\left(\varphi \right), z=r cos\left(\theta \right)$  

These coordinates appropriate for the symmetry of the problem. The Equation (1), expressed in these coordinates, is as follows:

$\left[\frac{{\partial }^2}{\partial r^2}+\frac{2}{r}\frac{\partial }{\partial r}\right]\psi \left(r,\theta ,\varphi \right)+\frac{1}{r^2}\widehat{{\mathcal{L}}^2}\left(\theta ,\varphi \right)\psi \left(r,\theta ,\varphi \right)+\frac{2m}{{\hslash }^2}\left[E-V\left(r,\theta ,\varphi \right)\right]\psi \left(r,\theta ,\varphi \right)=0$   (2)

${\widehat{\mathcal{L}}}^2\left(\theta ,\varphi \right)=\frac{{\partial }^2}{\partial {\text{θ}}^2}+\text{cotg}\left(\theta \right)\frac{\partial }{\partial \theta }+\frac{1}{si{n}^2\left(\theta \right)}\frac{{\partial }^2}{\partial {\varphi }^2}$

The potential energy of a particle which moves in a central and spherically symmetric field of force depends only upon the distance r between the particle and the center of force. Thus, the potential energy should be such as $V\left(r,\theta ,\varphi \right)=V\left(r\right)$ . Solution of the Equation (2) can be found by the method of separation of variables. To apply this method, it is assumed that the solution is in the form of

$\Psi \left(r,\theta ,\varphi \right)=R\left(r\right)Y\left(\theta ,\varphi \right)=R\left(r\right)|jm >$   (3)

in which R(r) is independent of the angles, and $Y\left(\theta ,\varphi \right)$  and $|\text{jm} >$  are independent of r. By substituting Equation (3) into Equation (2) and rearranging, the following Equation is obtained. In the Equation (3),m is not mass, it is magnetic quantum number.

$\left[\frac{{\partial }^2}{\partial r^2}+\frac{2}{r}\frac{\partial }{\partial r}\right]R\left(r\right)+\left\{\frac{2m}{{\hslash }^2}\left[E-V\left(r\right)\right]-\frac{C}{r^2}\right\}R\left(r\right)=0$   (4)

${\widehat{\mathcal{L}}}^2\left(\theta ,\varphi \right)\text{ Y}\left(\theta ,\varphi \right)+\text{C Y}\left(\theta ,\varphi \right)=0$   (5)

Here, C is a constant. Equation (5) is independent of the total energy E and of the potential energy V(r) therefore, the angular dependence of the wave functions is determined by the property of spherical symmetry, and admissible solutions of Equation (5) are valid for every spherically symmetric system regardless of the special form of the potential function. The solutions of the Equation (5) can be found in any quantum mechanics and mathematical physics text-books and the solutions are known as spherical harmonic functions, $Y\left(\theta ,\varphi \right)=Y_{\mathcal{l}\mu }\left(\theta ,\varphi \right),$  where $C=\mathcal{l}\left(\mathcal{l}+1\right),\mathcal{l}=0,1,2,3,\mathrm{...}$ are positive integer numbers and $\mu =-\mathcal{l}, -\mathcal{l}+1,\mathrm{...0...}+\mathcal{l}.$  Equation (4) is the radial SE (Schrödinger Equation). Substituting $C=\mathcal{l}\left(\mathcal{l}+1\right)$  and $R\left(r\right)=F\left(r\right)/r$  into Equation (4), the radial wave Equation is obtained as follow:

$\left\{\frac{d^2}{d{r}^2}+\frac{2m}{{\hslash }^2}\left[E-U\left(r\right)\right]\right\}F\left(r\right)=0$ ;$\frac{d^{2}F\left(r\right)}{d{r}^2}+[\alpha -U_e\left(r\right)=0$   (6)

Here $\alpha =\frac{2m}{{\hslash }^2}E$ ; $U\left(r\right)=V\left(r\right)+\frac{{\hslash }^2}{2m}\frac{\mathcal{l}\left(\mathcal{l}+1\right)}{r^2}$  is the effective potential energy, and $U_e\left(r\right)=\frac{2m}{{\hslash }^2}U\left(r\right)$ . here m is mass or reduced mass of particle.

Equation (6) is one dimensional differential equation. The solution of this one-dimensional differential equation has been given in.^1,2 The F(r) functions have been found by using the same procedure that is explained in these references. Two of these solutions are given as follows:

$F\left(r\right)=cosh\text{[k r}] [{\text{A e}}^{\text{i G}\left(\text{r}\right)}+{\text{B e}}^{\text{-iG}\left(\text{r}\right)}] ;$ $F\left(r\right)=sinh\text{[k r}] [{\text{A e}}^{\text{i G}\left(\text{r}\right)}+{\text{B e}}^{\text{-iG}\left(\text{r}\right)}]$  (7)

Here,

For $\alpha >U_e\left(r\right),$ (bound state), $k=\sqrt{-\alpha } , G\left(r\right)={\displaystyle \int \sqrt{-U_e\left(r\right)} }\text{dr} \text{;} [G\left(r\right)$  real function]. For $\alpha >U_e\left(r\right),$  (unbound state), $k=\sqrt{\alpha }, G\left(r\right)={\displaystyle \int \sqrt{-U_e\left(r\right)} } \text{dr} .$   $r_1 and r_2$  are the roots of the following Equation:

$\alpha -U_e\left(r\right)=0 or E-U\left(r\right)=0$   (8)

In some cases, using the following quantities can provide more conveniences:

$d=r_2- r_1, \left(r_1< r_2\right); r_0=\left(r_1+ r_2\right)/2; r_1=r_0 -d/2 ; r_2=r_0+d/2.$

If one takes $\left(r-r_0\right)$  instead of in the above functions, these can also be used when obtaining the solutions of the Equation (6). The A and B coefficients of the functions are determined by using the boundary and normalization conditions.

In bound states (in the wells), the normalized wave functions are as follows [  is taken as real function]:

$F_s\left(r\right)=A cos\text{[k r}] e^{\pm }{}^{\text{i} G\left(r\right)}$ $F_a\left(r\right)=B sin\text{[k r}] e^{\pm }{}^{i G\left(r\right)}$   (9)

or

$F_s\left(r\right)=A cos\text{[k }\left(\text{r}-{\text{r}}_{\text{0}}\right)] e^{\pm }{}^{i G\left(r-r0\right)}$ $F_a\left(r\right)=B sin\text{[k }\left(r-r_0\right)] e^{\pm }{}^{i G\left(r-r0\right)}$  (10)

$\text{A} \text{=} \text{B} \text{=} \sqrt{2/d}=\sqrt{2K/q};$  ; (s: symmetric; a: antisymmetric).

The bound state energies are given by the solution of the following Equation:

$K [r_2\left(E\right)-r_1\left(E\right)]=Kd=q$ ;$K=\sqrt{\left|\alpha \right|}=\sqrt{\frac{2\text{ m}}{{\hslash }^2}\left|E\right|} .$   (11)

Equation (11) is the quantization condition of energy in bound states. For q=2 the ground state (minimum energy) occurs; for $q=n \pi , \left(n=1,2,3,\mathrm{...}\right),$  the excited states occur. We have symmetric states for odd integer values of n and antisymmetric states for even integer values of n.

Consider a particle with mass or reduced mass m is in the central potential of V(r) in a coordinate system at the point (0,0) of the coordinate start. The variable r of the potential in this coordinate system is always positive. If the spin of the particle is also considered, the total angular momentum quantum number j should be taken instead of L. Thus, the effective potential is $\text{U}\left(\text{r}\right)=\text{V}\left(\text{r}\right)+\text{b}/{\text{r}}^2;[\text{b}={\hslash }^2\text{ j }\left(\text{j}+1\right)/\left(2\text{m}\right)]$ . This effective potential is usually a parabolic function in the bound states. In the bound states, the total energy is always negative and consequently the effective potential is also negative. Therefore,$\text{U}\left(r\right)<0$ should be in the bound states. When mass m vibrates in this effective potential, the term b of the potential creates an obstacle that tries to prevent vibration motion. This potential comes from the rotation of the mass m, that is, from the centrifugal motion. If there is no rotation, this term is zero. The solution of the Equation $\text{U}\left(r\right)=-E or \left|\text{U}\left(r\right)\right|=E$  are $r_1, r_2,r_3 and r_4$  values, depending on E. If the values $\left(r_3 and r_4\right)$  are real and non-zero, there is a potential barrier in the potential well. If this Equation is solved at a point $r=r_0$ , these roots are written also as follows: $r_1=r_0-d_1/2$ and $r_2=r_0+d_1/2$ and $r_3=r_0-d_3/2$  and $r_4=r_0-d_3/2$ . Here $d_1=\left(r_2-r_1\right),d_3=\left(r_4-r_3\right)$ and $r_0=\left(r_1+r_2\right)/2=\left(r_3+r_4\right)/2$ . If the origin of the coordinate system is taken as the point $r_0$ , these are $r_1=-d_1/2 and r_2=-d_1/2$  and $r_3=-d_3/2$ and $r_4=-d_3/2$ . The points $r_1 and r_2, and r_3 and r_4$ are the classic turning points of the $\text{U}\left(\text{r}\right)$  potential. Since $\text{U}\left({\text{r}}_{\text{1}}\right)=\text{U}\left({\text{r}}_2\right) and \text{U}\left({\text{r}}_3\right)=\text{U}\left({\text{r}}_4\right)$  are equal at the potential of the classical turning points. Thus, the following Equations can be written:

$U\left(-d_1/2\right)+U\left(+d_1/2\right)=2E$ $U\left(-d_3/2\right)+U\left(+d_3/2\right)=2 E$ Since $E={\text{ m}}_h{\text{ q}}^2/d_i^2\left(E\right) , \left({\text{ m}}_h=\frac{{\hslash }^2}{2\text{ m}} \right) .$

these Equations can also be written as follows:

$U\left(-d_1/2\right)+U\left(+d_1+2\right)=2 m_h q^2/d_i^2\left(E\right)$ $U\left(-d_3/2\right)+U\left(+d_3+2\right)=2 m_h q^2/d_3^2\left(E\right)$  

The solution of these two Equations has the same energy. It is therefore sufficient to solve one of these two Equations to find the energy values. When these Equations cannot be solved analytically, numerical solutions are made, and energy values are found. When one of these two Equations is solved, two energies based on q are obtained. One of these energies (+) and the other (-) becomes and their absolute values are equal. The (-) sign indicates that the particle is bound. For q=2 the ground state (minimum energy) occurs; for $q=n \pi , \left(n=1,2,3,\mathrm{...}\right),$  the excited states occur. We have symmetric states for odd integer values of  and antisymmetric states for even integer values of . This problem is useful in some cases if it is solved in two wells.

Solutions become easier when you divide a given potential into two parts. This separation process will be given here. If the potential is given as $V\left(r\right)=V_0\left(r\right)-V_{00},[V_0\left(r\right)>0 and V_{00}> 0],$ the effective potential is $\text{U}\left(\text{r}\right)=V_0\left(r\right)-V_{00}+\frac{b}{r^2}<0$  in the bound states. Here, $-V_{00}$  is the depth of the potential well. Let us find the maximum and minimum values of this effective potential $\text{U}\left(\text{r}\right)$ et the roots of the Equation $\text{U'}\left(\text{r}\right)=0,$   $r_{m1} and r_{m2} be. r_0=\left(r_{m1}+r_{m1}\right)/2$  is the point where the potential receives the smallest values $U\left(r_{m1}\right) and U\left(r_{m2}\right)$  and the largest value $U\left(r_0\right)$ . Let $U_0=U\left(r_0\right) -V_{00}$ Thus $\text{U}\left(\text{r}\right)=V_0\left(r\right)-U+\frac{b}{r^2}<0$ can be written. By solving this $\text{U}\left(\text{r}\right)$  potential directly, energy values and wave functions can be found. However, if this potential is divided into two parts with an obstacle in the middle, there may be some convenience. The obstacle in the two potential wells comes from rotational energy and the potential $[V_0\left(r\right)-U_0]$ . Therefore, the $\text{U}\left(\text{r}\right)$  potential can be written as the sum of two parts as follows:

$U\left(r\right)=V_0\left(r\right)-U_0+\frac{b}{r^2}=U_w\left(r\right)+U_b\left(r\right)$ ;$[U_w\left(r\right)=V_0\left(r\right)-U_0 ; U_b\left(r\right)=\frac{b}{r^2}]$  (12)

Here, the ${\text{U}}_{\text{w}}\left(\text{r}\right)$ potential is the vibration part of the $\text{U}\left(\text{r}\right)$  potential, and the ${\text{U}}_{\text{b}}\left(\text{r}\right)$  potential is total of the rotational and the other obstacle potential parts of the potential $\text{U}\left(\text{r}\right)$ .$U_0$ is the depth of the potential well. If the coordinate start is taken at the point $\left(r_0,-U_0\right)$  in this new coordinate system, $U_b\left(r\right)=\frac{b}{r^2}$  and $U_w\left(r\right)=V_0\left(r\right)$ . Thus, the effective potential is written as follows:

$U\left(r\right)=V_0\left(r\right)+\frac{b}{r^2}=U_w\left(r\right)+U_b\left(r\right)$ ;$[U_w\left(r\right)=V_0\left(r\right) ; U_b\left(r\right)=\frac{b}{r^2}]$   (13)

The graph of this potential is shown in Figure 1. (Shape of the U(r) function $\left(r_0,-U_0\right)$ in the coordinate system). In this way, three domains I, II, III are obtained. Thus, by solving the Equation (13), E energy values are found.

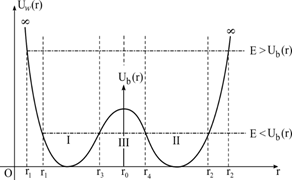
Figure 1 The plot of the potential U(r) in the form of two wells; the points r₁,r₂,r₃,r₄ are classic turning points.

The functions $U_w\left(r\right) and U_b\left(r\right)$ are symmetrical functions according to point $r_0$ . The $U_b\left(r\right)$  function is an obstacle function located in the midpoint of the well $U_w\left(r\right)$  function. The quantities $\left(r_1,r_2,r_3,r_4\right)$ that are the solution of the Equation $U\left(r\right)=E$ are depending on $r_0$ . As seen in Figure 1, the roots of the Equation, $U\left(r\right)=E$  are $\left(r_1, r_2, r_3, r_4\right)$ and the roots of $U_b\left(r\right)=E$  are $\left(r_3 , r_4\right),$ the roots of $U_w\left(r\right)=E$ are $\left(r_1 , r_2\right)$ . From there, the following values are obtained:

$\frac{r_1+r_2}{2}=\frac{r_3+r_4}{2}=0 ; d_1=r_3-r_1 ; d_2=r_2-r_4 ; d_1=d_2 ; d_3=r_4-r_3 ; d=r_2-r_1$

$[d_1, d_2, d_3]$ are respectively the widths of the region $\left(\text{I,II,III}\right)$ . Since $d_1=d_2$ , it is sufficient to make a solution in one of the regions (I) and (II). Particle is unbound in the region , it cannot remain in this area continuously, it can pass from region II to region I or from region I to region II by tunneling with equal probability. Here the probability of passing coefficient is calculated.

Example: Three axial deformed harmonic oscillator potential (anisotropic harmonic oscillator potential) (Nilson model in the nuclear physics)

Effective potential

The nucleus is assumed to have a spherical shape in the shell model. Therefore, particles move in a spherically symmetric potential. There are, however, convincing arguments that nuclei with the neutron and proton numbers sufficiently far from the magic numbers have no spherical symmetry ellipsoidal shapes. In this case, it is said that the deformed shell model. In deformed shell model calculations, it is used the three-dimensional anisotropic harmonic oscillator potential which is given as follows:

$V_0\left(x,y,z\right)=\frac{1}{2}\mu \left({\omega }_x^2{x}^2+{\omega }_y^2{y}^2+{\omega }_Z^2{Z}^2\right)$  (14)

Here,μ is mass or reduced mass. In the case of deformed nuclei, it is generally restricted to axially symmetric nuclei and it taken the z -axis as symmetry axis. So, it is accepted ${\omega }_X={\omega }_y={\omega }_{\perp }\ne {\omega }_z$  in the anisotropic harmonic oscillator potential. The motion of a particle in an axially symmetric potential, with additional symmetry plane, perpendicular to symmetry axis was described by Nilsson. The no-spherical nuclei have the shape of an ellipsoid of revolution. It is, however, possible that some transitional nuclei have shapes of a three-axial ellipsoid. It is also possible that the shapes of excited states differ from the ground state shapes and that some exited states have three axial ellipsoidal forms. In the three axial cases, ${\omega }_X\ne {\omega }_y\ne {\omega }_z$ . The no-axial shape is characterized by two parameters $\epsilon and \gamma$ . For $\epsilon >0, \gamma =0^0$  situation corresponds to the axially symmetric prolate ellipsoid,$\gamma ={60}^0$ corresponds to the oblate ellipsoid. When $\gamma \ne 0^0 and \gamma \ne {60}^0$ , the ellipsoid has no axial symmetry, and the projection quantum number of the total angular momentum on any axis is not one conserved quantity. The angular frequencies ${\omega }_x,{\omega }_y,{\omega }_z$ relate to the deformation parameters $\epsilon and \gamma$ by the following expressions:

${\omega }_x={\omega }_0\left(\epsilon ,\gamma \right)\left[1-\frac{2}{3}\epsilon cos\left(\gamma +\frac{2\pi }{3}\right)\right]$ ;${\omega }_y={\omega }_0\left(\epsilon ,\gamma \right)\left[1-\frac{2}{3}\epsilon cos\left(\gamma +\frac{2\pi }{3}\right)\right]$ ${\omega }_z={\omega }_0\left(\epsilon ,\gamma \right)\left[1-\frac{2}{3}\epsilon cos\left(\gamma \right)\right]$   (15)

If it is required a constant volume as deformation changes, it needs:

${\omega }_x{\omega }_y{\omega }_z={\omega }_{00}^3$   (16)

From Equation (16), we get the following value:

${\omega }_0\left(\epsilon ,\gamma \right)=3{\omega }_{00}{[27=9{\epsilon }^2-2{\epsilon }^3 cos\left(3\gamma \right)]}^{-1/3}$   (17)

As can be seen from Equation (17), if $\epsilon =0,$  isotropic state is obtained. Let us express the potential given in Equation (14) the following spherical coordinates:

$\text{x=} \text{r} sin\left(\theta \right) cos\left(\varphi \right), y=r sin\left(\theta \right)sin\left(\varphi \right), z=r cos\left(\theta \right)$   (18)

If the potential given in Equation (14) is calculated by considering Equations (15), (16) and (17), the following function is obtained:

$V_0\left(r,\epsilon ,\gamma \right)=\frac{1}{2}\mu {\omega }_{00}^2{r}^2[A\left(\epsilon ,\gamma \right) si{n}^2\left(\theta \right) co{s}^2\left(\varphi \right)+B\left(\epsilon ,\gamma \right) si{n}^2\left(\varphi \right) si{n}^2\left(\varphi \right)+C\left(\epsilon ,\gamma \right) co{s}^2\left(\theta \right)]$  (19)

$A\left(\epsilon ,\gamma \right)=\frac{{\left[3+2\epsilon sin\left(\frac{\pi }{6}+\gamma \right)\right]}^2}{{\left[27=9{\epsilon }^2-2{\epsilon }^3 cos\left(3\gamma \right)\right]}^{2/3}};$ $B\left(\epsilon ,\gamma \right)=\frac{{\left[3+2\epsilon sin\left(\frac{\pi }{6}-\gamma \right)\right]}^2}{{\left[27-9{\epsilon }^2-2{\epsilon }^3 cos\left(3\gamma \right)\right]}^{2/3}};$ $C\left(\epsilon ,\gamma \right)=\frac{{\left[3-2\epsilon cos\left(\gamma \right)\right]}^2}{{\left[27-9{\epsilon }^2-2{\epsilon }^3 cos\left(3\gamma \right)\right]}^{2/3}};$   (20)

${\beta }^2=A\left(\epsilon ,\gamma \right) si{n}^2\left(\theta \right) co{s}^2\left(\varphi \right)+B\left(\epsilon ,\gamma \right) si{n}^2\left(\theta \right) si{n}^2\left(\varphi \right)+C\left(\epsilon ,\gamma \right) co{s}^2\left(\theta \right)$  

${\beta }^2=A\left(\epsilon ,\gamma \right) [1- co{s}^2\left(\theta \right)] co{s}^2\left(\varphi \right)+B\left(\epsilon ,\gamma \right) [1- co{s}^2\left(\theta \right)][1- co{s}^2\left(\theta \right)]+C\left(\epsilon ,\gamma \right) co{s}^2\left(\theta \right)$  

${\beta }^2=B\left(\epsilon ,\gamma \right) [C\left(\epsilon ,\gamma \right)-B \left(\epsilon ,\gamma \right)-\{A\left(\epsilon ,\gamma \right)-B\left(\epsilon ,\gamma \right)\} co{s}^2\left(\varphi \right)] co{s}^2\left(\theta \right)+\left[A\left(\epsilon ,\gamma \right)-B\left(\epsilon ,\gamma \right)\right] co{s}^2\left(\theta \right)$  (21)

If γ is exceedingly small, then $\sin \left(\gamma \right)\approx 0$  and $\text{A}\approx \text{B}$ (symmetric ellipsoid form) can be taken. Thus, ${\text{ β}}^2$ can be taken as follows:

${\beta }^2=B\left(\epsilon ,\gamma \right)+ [C\left(\epsilon ,\gamma \right)-B \left(\epsilon ,\gamma \right)] co{s}^2\left(\theta \right)=B\left(\epsilon ,\gamma \right)+\left[C\left(\epsilon ,\gamma \right)-B\left(\epsilon ,\gamma \right)\right]\left[\frac{1}{3}+\frac{2}{3}\sqrt{\frac{4\pi }{5}}{Y}_0^2\right]$  (22)

$Y_0^2$  is spherical harmonic function. Thus, the anisotropic harmonic oscillator potential becomes as follows:

$V_0\left(r,\epsilon ,\gamma \right)=\frac{1}{2}\mu {\omega }_{00}^2{r}^2{\beta }^2\left(\epsilon ,\gamma \right)$   (23)

With this potential, the effective potential $U\left(r,\epsilon ,\gamma \right)$    is obtained as follows:

$U\left(r,\epsilon ,\gamma \right)=V_0\left(r,\epsilon ,\gamma \right)+\frac{{\hslash }^2}{2\mu r^2}j\left(j+1\right)=\frac{1}{2}\mu {\omega }_{00}^2{r}^2{\beta }^2\left(\epsilon ,\gamma \right)+\frac{{\hslash }^2}{2\mu r^2}j\left(j+1\right)$  (24)

Here, ${\omega }_{00}$ is the isotropic oscillator angular frequency and total angular momentum quantum number. The Coulomb potential must be added to the potential given in Equation (24) when the charged particle levels are calculated. The Coulomb potential in the spherical case, neglecting the effect of the surface, is as follows:

$V_c\left(r\right)=\frac{\left(Z-1\right) e^2}{r}\left\{\begin{array}{c}\frac{3\text{ r}}{2{\text{ R}}_0}-\frac{1}{2}{\left(\frac{\text{r}}{{\text{R}}_0}\right)}^2 , for r\le {\text{R}}_0\\ 1 , for r>{\text{R}}_0 \\ \end{array}\right\}$

Here,${\text{R}}_0$ is the radius of the spherical nucleus and Z is the charge number. Thus, in the nucleus, $\text{ r}\le {\text{R}}_0$ , we have as follows:

$V_c\left(r\right)=b_c+a_c r^2$ ; $\left[a_c=- \frac{\left(Z-1\right)e^2}{2 R_0^3} , b_c=\frac{3 \left(Z-1\right)e^2}{2 R_0} \right]$   (25)

In the quadratic deformed case, the Coulomb potential is obtained as follows:

$V_c\left(r\right)=\frac{3\left(Z-1\right)e^2}{2R_0}\{-8.9723-3.3241 \epsilon +8.14235\sqrt{1.5+\epsilon }+a_c{r}^2, for r\le R_0\}$  

$V_c\left(r\right)=\frac{\left(Z-1\right)e^2}{R_0}\{\frac{R_0}{r}-4.76142-1.58717 \epsilon +3.88768\sqrt{1.5+\epsilon }, for r>R_0\}$  

Because in the nucleus $r\le R_0,$ in the case quadratic, the Coulomb potential can be rewritten as follows:

$V_c\left(r\right)=b_c\left(\epsilon \right)+a_c r^2$ ;

$[a_c=-\frac{\left(Z-1\right)e^2}{2 R_0^3}, b_c \left(\epsilon \right)=\frac{3\left(Z-1\right)e^2}{2 R_0}\left(-8.9723-3.3241 \epsilon +8.14235\sqrt{1.5+\epsilon }\right)$   (26)

It is seen that for $\epsilon =0$ , Equation (26) is equal to Equation (25). On the other hand, the total wave function  is $\psi \left(r,\theta \varphi \right)=R\left(r\right)\left|\mathcal{l}jm>=\frac{F\left(r\right)}{r}\right|\mathcal{l}jm>$ and the radial SE is written as follows:

$\frac{d^{2}F\left(r\right)}{d{r}^2}\left|\mathcal{l}jm>+\frac{2\mu }{{\hslash }^2}\left[E-U\left(r,\epsilon ,\gamma \right)\right]F\left(r\right)\right|\mathcal{l}jm>=0$ ;$\frac{d^{2}F\left(r\right)}{d{r}^2}\left|\mathcal{l}jm>+\frac{2\mu }{{\hslash }^2}F\left(r\right)\left[E-U\left(r,\epsilon ,\gamma \right)\right]\right|\mathcal{l}jm>=0$   (27)

In Equation (27), $\left[E-U\left(r,\epsilon ,\gamma \right)\right]|\mathcal{l}jm>$ is calculated as follows:

$\left[E-U\left(r,\epsilon ,\lambda \right)\right]\left|\mathcal{l}\text{jm}>=\text{E}\right|\mathcal{l}\text{jm}>-U\left(r,\epsilon ,\gamma \right)|\mathcal{l}\text{jm}>$

$U\left(r,\epsilon ,\gamma \right)|\mathcal{l}jm>=\left[\frac{1}{2}\mu {\omega }_{00}^2{\text{r}}^2{\beta }^2\left(\epsilon ,\gamma \right)+\frac{{\hslash }^2}{2\mu {\text{ r}}^2}j\left(j+1\right)\right]|\mathcal{l}jm>$

${\beta }^2\left(\epsilon ,\gamma \right)]|\mathcal{l}\text{jm}>={\beta }^2|\mathcal{l}\text{jm}>=\left\{B\left(\epsilon ,\gamma \right)+\left[\text{C}\left(\epsilon ,\gamma \right)-\text{B}\left(\epsilon ,\gamma \right)\right]\left[\frac{1}{3}+\frac{2}{3}\sqrt{\frac{4\pi }{5}}{Y}_0^2\right]\right\}|\mathcal{l}\text{jm}>$  (28)

${\beta }^2\left(\epsilon ,\gamma \right)]\left|\mathcal{l}\text{jm}>={\beta }^2\right|\mathcal{l}\text{jm}>=\left\{\text{B}\left(\epsilon ,\gamma \right)+\left[\text{C}\left(\epsilon ,\gamma \right)-\text{B}\left(\epsilon ,\gamma \right)\right]co{s}^2\left(\theta \right)\right\} |\mathcal{l}\text{jm}>$

If we calculate ${\text{Y}}_0^2|\mathcal{l}\text{jm}\rangle ={\text{a}}_{20}|\mathcal{l}\text{jm}\rangle$ in Equation (28), by the Wigner-Eckart theorem, we have found the following value:

${\text{a}}_{20}\left(\mathcal{l},\text{j},\text{m}\right)-\sqrt{\frac{\pi }{2\mathcal{l}+1}}\frac{j+j^2-3m^2}{2j\left(j+1\right)}={\text{a}}_{20}$

Thus, ${\beta }^2\left(\epsilon ,\gamma ,{\text{a}}_{20}\right)$ are written as follows:

${\beta }^2\left(\epsilon ,\gamma ,a_2{}_0\right)=B\left(\epsilon ,\gamma \right)+\left[C\left(\epsilon ,\gamma \right)-B\left(\epsilon ,\gamma \right)\right]\left[\frac{1}{3}+\frac{2}{3}\sqrt{\frac{4\pi }{5}}{a}_2{}_0\right]$   (29)

So, we have found the effective potential for anisotropic harmonic oscillator as follows.

$U\left(r;\epsilon ,\gamma ,a_2{}_0\right)=\frac{1}{2}\mu {\omega }^2{{}_0}_0{\beta }^2\left(\epsilon ,\gamma ,a_0{}_0\right)r^2+\frac{{\hslash }^2}{2\mu r^2}j\left(j+1\right)=a{r}^2+\frac{b}{r^2}=U\left(r\right)$  (30)

$a=\frac{1}{0}\mu {\omega }^2{{}_0}_0{\beta }^2\left(\epsilon ,\gamma ,a_2{}_0\right)=\frac{1}{2}\mu {\omega }^2;b=\frac{{\hslash }^2}{2_{\mu }}j\left(j+1\right);{\omega }^2={\omega }^2{{}_0}_0{\beta }^2\left(\epsilon ,\gamma ,a_2{}_0\right)$  (31)

In the case of electric charged particle, the Coulomb potential should be also added to this effective potential.

Consider $U_w\left(r\right)={\text{a r}}^2$ and $U_b\left(r\right)=\frac{{\hslash }^2}{2\mu }\frac{\text{j }\left(\text{j}+1\right)}{{\text{r}}^2}=\frac{\text{b}}{{\text{r}}^2} , \left[b=m_h\text{ j }\left(\text{j}+1\right),m_h=\frac{{\hslash }^2}{2\mu }\right].$  Thus, according to (30), we have:

$U\left(r\right)=V_0\left(r\right)+ \frac{b}{r^2}=U_w\left(r\right)+U_b\left(r\right) ;$   $\left[ U_w\left(r\right)= V_0\left(r\right)=a r^2 ; U_b\left(r\right)= \frac{b}{r^2}\right]$ .

Solution of the Equation $\text{U}\left(\text{r}\right)={\text{E}}_{\text{q }}$ gives the following values:

${\text{r}}_1=-\sqrt{\frac{{\text{E}}_{\text{q}}+\sqrt{{\text{E}}_{\text{q}}^2-4\text{ a b}}}{2\text{ a}}};$ ${\text{r}}_2=\sqrt{\frac{{\text{E}}_{\text{q}}+\sqrt{{\text{E}}_{\text{q}}^2-4\text{ a b}}}{2\text{ a}}};$ ${\text{ r}}_3=-\sqrt{\frac{{\text{E}}_{\text{q}}-\sqrt{{\text{E}}_{\text{q}}^2-4\text{ a b}}}{2\text{ a}}};$ ${\text{ r}}_4=\sqrt{\frac{{\text{E}}_{\text{q}}-\sqrt{{\text{E}}_{\text{q}}^2-4\text{ a b}}}{2\text{ a}}}$ .

$\frac{{\text{r}}_1+{\text{r}}_2}{2}=\frac{{\text{r}}_3+{\text{r}}_4}{2}={\text{r}}_0=0;{\text{ d}}_1={\text{r}}_3-{\text{r}}_1;{\text{ d}}_2={\text{r}}_2-{\text{r}}_4;{\text{ d}}_1={\text{d}}_2;{\text{ d}}_3={\text{r}}_4-{\text{r}}_3;\text{ d}={\text{r}}_2-{\text{r}}_1$ .

Now, we will solve this problem in three cases as follows.

In this case, the following equation can be written according to the quantization condition of energy:

$\text{K d}={\text{E}}_{\text{q}}{\text{ or K}}^2{\text{d}}^2=E_q^2 ;[\text{K}=\sqrt{\frac{2\mu {\text{ E}}_q}{{\hslash }^2}}]$

The following energy value is obtained from the solution of this equation.

$E_q=\frac{\sqrt{\text{a}}{\hslash }^2{q}^2}{2\sqrt{2\mu }\sqrt{{\hslash }^2{q}^2-8\mu \text{ b}}};[E_q>U_b\left(r\right)]$  (32)

If the energy ${\text{E}}_{\text{q}}$  does not depend on the angular momentum quantum number j, i.e., rotation, energy is purely vibrational energy. In this case, $b=0 and E_q=\frac{1}{2}\hslash \omega$ .

In this case, since ${\text{ d}}_1={\text{d}}_2$ , equal energy values are obtained in (I) and (II) regions. So, the following equation can be written according to the quantization condition of energy:

${\text{K d}}_1={\text{E}}_{\text{q}}{\text{ or K}}^2{\text{d}}_1^2=E_q^2 ;[\text{K}=\sqrt{\frac{2\mu {\text{ E}}_q}{{\hslash }^2}}]$

The following energy values are obtained from the solution of this equation.

$E_q^{\left(1\right)}=\frac{\sqrt{a \mu \left(4 b \mu +{\hslash }^2{q}^2\right)+\delta \left(a,b,q\right)}}{\mu }$ ;$E_q^{\left(2\right)}=\frac{\sqrt{a \mu \left(4 b \mu +{\hslash }^2{q}^2\right)-\delta \left(a,b,q\right)}}{\mu }$  (33)

$\delta =2\sqrt{2 {\text{a}}^2\text{b }{\mu }^3\left(2\text{ b }\mu +{\hslash }^2{\text{q}}^2\right)}$

If the values of b are put in place, the following values depending on (a, j, q) are obtained:

$E_{q1}\left(a,j,q\right)=\frac{\sqrt{a {\hslash }^2\left(2j+2j^2+q^2\right)\mu +\delta }}{\mu }$ ; $E_{q2}\left(a,j,q\right)=\frac{\sqrt{a {\hslash }^2\left(2j+2j^2+q^2\right)\mu -\delta }}{\mu }$ . (34)

$\delta \left(a,j,q\right)=2a{\hslash }^2\mu \sqrt{j\left(1+j\right)\left(j+j^2+q^2\right)}$  

Then, in case ${\text{ E}}_{\text{q}}<{\text{U}}_{\text{b}}\left(\text{r}\right)$ , there are two equal energy values in regions (I) and (II). As seen in Figure 1, the ${\text{U}}_{\text{b}}\left(\text{r}\right)$  barrier potential located between (I) and (II) potential wells divides the energy of the particle into two. While the particle is oscillating in these wells, when the particle reaches the r₃ (or r₄) point, some of its energy passes from the III region to the II (or I) region by tunneling, and some of it is reflected from the r₃ (or r₄) point. This transition is equally likely for both parties. (This passing probability will be calculated below). Thus, the potential barrier divides the energy of the particle in two. The rotational potential due to angular momentum always splits the energy into two parts. This phenomenon may be a way to find the angular momentum of a particle. When $j=0,\left(\delta =0\right)$ in (34), there is only one energy. So, the ${\text{ U}}_{\text{b}}\left(\text{r}\right)$  barrier cuts a single energy into two parts. These double energy splits are observed at small vibrations in some molecules such as ammonia. Many double wells are proposed to explain these energy splits, although there is no need for them. Because this energy splitting occurs in small vibrations for all particles with angular momentum.

We consider the effective potential given here as a whole. We will solve the two wells at the bottom of the potential well in general, without considering them separately.

$\text{U}\left(\text{r}\right)={\text{ V}}_0\left(\text{r}\right)+\frac{\text{b}}{{\text{r}}^2}={\text{U}}_{\text{w}}\left(\text{r}\right)+{\text{U}}_{\text{b}}\left(\text{r}\right);$ $\left[{\text{ U}}_{\text{w}}\left(\text{r}\right)={\text{ V}}_0\left(\text{r}\right);{\text{ U}}_{\text{b}}\left(\text{r}\right)=\frac{\text{b}}{{\text{r}}^2};{\text{ V}}_0\left(\text{r}\right)={\text{a r}}^2\right]$

Solution of the Equation $\text{U}\left(\text{r}\right)={\text{E}}_{\text{q }}$ gives the following r values:

$r_1=-\sqrt{\frac{E_q+\sqrt{E_q^2-4 a b}}{2 a}} ; r_2=\sqrt{\frac{E_q+\sqrt{E_q^2-4 a b}}{2 a}} ;$  $r_3=-\sqrt{\frac{E_q-\sqrt{E_q^2-4 a b}}{2 a}} ; r_4=\sqrt{\frac{E_q-\sqrt{E_q^2-4 a b}}{2 a}}$ ;

${\text{d}}_1={\text{r}}_2-{\text{r}}_1;{\text{ d}}_3={\text{r}}_4-{\text{r}}_3$ .

Positive root of Equation $d_1^2 \left[U\left(r_1\right)+U\left(r_2\right)\right]=2 m_h q^2$  is $E_{q1}=\frac{\sqrt{a} m_h q^2}{2 \sqrt{m_h q^2-4 b}}=\frac{q^2 \hslash \omega }{4 \sqrt{q^2-4 j \left(j+1\right)}}$  .

Positive root of Equation $d_3^2 \left[U\left(r_3\right)+U\left(r_4\right)\right]=2 m_h q^2$  is $E_{q3}=\frac{\sqrt{a} m_h q^2}{2 \sqrt{m_h q^2-4 b}}=\frac{q^2 \hslash \omega }{4 \sqrt{q^2-4 j \left(j+1\right)}}$  .

From here it is seen that $E_{q1}=E_{q3}$ . Since the particle is not bound in zone so energy is obtained as follows.

$E_q\left(q,j\right)=\frac{\sqrt{a} m_h q^2}{2 \sqrt{m_h q^2-4 b}}=\frac{q^2 \hslash \omega }{4 \sqrt{q^2-4 j \left(j+1\right)}}$   (35)

It is seen that the energy of (32) and the energy of (35) are the same for $\text{ j}=0$ . We have for $\text{q}=2,$  the minimum (ground) state energy; for $\text{q=n }\pi ,\left(n=1,2,\mathrm{3...}\right)$  the exited state energies. We have symmetric states for odd integer values of n; antisymmetric states for even integer values of .

Here the solutions are made for the potential ${\text{V}}_0\left(\text{r}\right)={\text{a r}}^2$ and all solutions could be done analytically. If the potential is not a potential that can be solved analytically (as Saxon-Wood potential, trigonometric potentials etc.), numerical solutions can be made in the same way.

If the potential ${\text{ U}}_{\text{w}}\left(\text{r}\right)$  potential is an isotropic harmonic oscillator potential, therefore, the mass or reduced mass m in zone (I) makes a harmonic motion. If there were no (III) barriers, there would be only one energy value. So, the energy value would be corrupt. With such a two-well solution, corruption is eliminated. Therefore, total energy would be 32 or (35) if there were not the ${\text{U}}_{\text{b}}\left(\text{r}\right)$  obstacle at the point $r_0$ . According to the function (10), the radial normalized wave functions can be written as follows:

$\text{Q}\left(\text{r}\right)={\text{m}}_1{{\displaystyle \int }}^{\text{}}\sqrt{\left|{\text{U}}_{\text{w}}\left(\text{r}\right)\right|}\text{ dr}=\text{Q}\left(\text{r}\right)$ ;$\left[m_1=\sqrt{\frac{2 m}{{\hslash }^2}}=\frac{\sqrt{2 m}}{\hslash } \right]$

 (36)

For the state of $E_q$ , the independent of time and time dependent normalized wave functions are as follows, respectively:

$F^s$  (r)=A cos [K r] ${\text{e}}^{\pm \text{i Q}\left(\text{r}\right)}$  ;

F^a (r)= B sin [K r] ${\text{e}}^{\pm \text{i Q}\left(\text{r}\right)}$ .

${\text{F}}^{\text{s}}\left(\text{r},\text{t}\right)=\text{A }\cos \left[\text{K r}\right]{\text{e}}^{\pm \text{i Q}\left(\text{r}\right)}{\text{e}}^{- \frac{\text{i}}{\hslash }{\text{ E}}_{\text{q}}\text{ t}} ;$ ${\text{F}}^{\text{a}}\left(\text{r},\text{t}\right)=\text{B }\sin \left[\text{K r}\right]{\text{e}}^{\pm \text{i Q}\left(\text{r}\right)}{\text{e}}^{- \frac{\text{i}}{\hslash }{\text{ E}}_{\text{q}}\text{ t}}$ . (37)

$\text{A}=\text{B}=\sqrt{2\text{ K}/\text{q}},\text{ K}=\sqrt{\frac{2\text{ m}}{{\hslash }^2}{\text{E}}_{\text{q}}}={\text{m}}_1\sqrt{{\text{E}}_{\text{q}}}.$

The independent of time and time-dependent total normalized wave functions are as follows, respectively:

${\psi }^{\text{s}}\left(\text{r},\theta ,\varphi \right)=\text{R}\left(\text{r}\right)|\text{jm}>=\frac{{\text{F}}^{\text{s}}\left(\text{r}\right)}{\text{r}}|\text{jm}>;$ ${\psi }^{\text{a}}\left(\text{r},\theta ,\varphi \right)=\text{R}\left(\text{r}\right)|\text{jm}>=\frac{{\text{F}}^{\text{a}}\left(\text{r}\right)}{\text{r}}|\text{jm}>$   (38)

${\psi }^{\text{a}}\left(\text{r},\theta ,\varphi ,\text{t}\right)=\text{R}\left(\text{r}\right)|\text{jm >}=\frac{{\text{F}}^{\text{a}}\left(\text{r}\right)}{\text{r}}|\text{jm >}{\text{e}}^{- \frac{\text{i}}{\hslash }{\text{ E}}_{\text{q}}\text{ t}};$ ${\psi }^{\text{s}}\left(\text{r},\theta ,\varphi ,\text{t}\right)=\text{R}\left(\text{r}\right)|\text{ jm}>=\frac{{\text{F}}^{\text{s}}\left(\text{r}\right)}{\text{r}}|\text{ jm}{>}^{- \frac{\text{i}}{\hslash }{\text{ E}}_{\text{q}}\text{ t}}$