The escape velocity of an object and the necessary supplied velocity to achieve it are calculated in this paper for several situations of the body, such as from rest, in free fall, and in orbit (several orbital cases are studied). This article clearly and concisely shows that escape velocity and supplied velocity are different magnitudes, as these concepts often cause confusion for students. To address this issue, different initial situations of the body that tries to escape are studied to show in the clearest and the most generic possible way the strategies to address escape problems without conceptual errors.

Keywords: escape velocity, gravitation, conservation of energy, theorem of living forces

Cosmology and gravitation are usually one of the most interesting and motivating topics for pre-university physics students. Thus, in recent years, several didactic articles have been published on this branch of physics.^1,2 One of the experiences that most surprises students when they first study the subject of gravitation is the escape velocity of a body. In this respect, there is a lot of classical literature on the calculation of the escape velocity, but there are also very interesting didactic articles on this branch of physics^3,4 but also very new didactic articles that show new approaches to the problem.¹ In addition, there are recent articles on this subject at an advanced level of research, which shows the current importance of the problem.⁷which shows the current importance of this concept.

However, despite all the existing literature, even today there are still errors and misconceptions about escape velocity. Specifically, pre-university students confuse the escape velocity of a body with the supplied velocity that must be provided to the body in order for it to escape. This topic has not been studied or given sufficient attention in the current literature, and it is the novelty and motivation of this article, which aims to clarify the difference between these two related, but not equal, quantities.

The escape velocity is defined as the minimum velocity that an object must have to escape the gravitational pull of a more massive body.^3,4 To achieve this escape velocity, a certain amount of energy or work $\left(E_s\right)$ in such a way that the principle of conservation of energy is fulfilled, which states that the work done must be equal to the variation of mechanical energy:⁵

$E_s=\Delta E_M=E_{Mf}-E_{Mi}$   (1)

We understand that a body escapes from a gravitational attraction when it reaches infinity with zero velocity.³ Therefore, the final mechanical energy will be zero $\left(E_{Mf}=0\right),$  as we take the origin of potential energies at infinity as usual⁵ (the potential energy cancels out, $E_{Pf}=0$ ) and the velocity at which it arrives is zero (the kinetic energy cancels out $E_{cf}=0$ ), so we can rewrite the principle of energy conservation as:

$E_{Mi}+E_s=0$   (2)

On the other hand, it must be fulfilled that the work done $\left(E_s\right)$ to overcome the initial mechanical energy $\left(E_{Mi}\right)$  of the body must be equal to the variation of the kinetic energy of that body, as established by the theorem of the living forces.⁵

$E_s=\Delta E_c=\frac{1}{2}m\left(v_f^2-v_i^2\right)$   (3)

Where $v_i$ is the initial velocity of the object before the energy was supplied to it $E_s$ ; is the velocity after supplying it with the energy necessary for it to escape. This final velocity is what we will call the escape velocity $\left(v_e\right),$  since it is the velocity that the object will have after the application of the $E_s$ and therefore it will be the necessary velocity that an object must have to escape from the gravitational attraction.³ We will consider that the energy input $\left(E_s\right)$  occurs instantaneously, so we will not discuss the accelerations of the system.³ Moreover, taking into account that the escape velocity is the final velocity that the body acquires after supplying it with energy, we can write this velocity in vector terms as:

${\overrightarrow{\nu }}_f={\overrightarrow{\nu }}_e={\overrightarrow{\nu }}_i+{\overrightarrow{\nu }}_s$   (4)

Where ${\overrightarrow{\nu }}_s$  corresponds to the velocity supplied through the $E_s$  and should not be confused with the escape velocity $\left({\overrightarrow{\nu }}_e\right),$  which is the final velocity that the body acquires after the application of the $E_s$  and is the minimum velocity that the object must have to escape the gravitational attraction. These two velocities coincide only in the case where the initial velocity $\left({\overrightarrow{\nu }}_i\right)$ is zero.

From the equations (2) and (3) an expression can be obtained to calculate the escape velocity in any situation:

$v_e^2=v_i^2-\frac{2}{m}{E}_{Mi}$   (5)

Considering the velocity composition shown in (4) the expression can be achieved to obtain the velocity that needs to be supplied to the object to reach the escape velocity:

${\left|{\overrightarrow{v}}_i+{\overrightarrow{v}}_s\right|}^2=v_i^2-\frac{2}{m}{E}_{Mi}$   (6)

Developing the modulus of the vector and clearing the supplied velocity we obtain:

${\left|{\overrightarrow{v}}_s\right|}^2+2\cdot {\overrightarrow{v}}_s. {\overrightarrow{v}}_s+\frac{2}{m}{E}_{Mi}=0$   (7)

Where the product ${\overrightarrow{v}}_s\cdot {\overrightarrow{v}}_i$  is a scalar product, i.e:

${\left|{\overrightarrow{v}}_s\right|}^2+2\cdot \left|{\overrightarrow{v}}_s\right| . \left|{\overrightarrow{v}}_i\right| .\cos \alpha +\frac{2}{m}{E}_{Mi}=0$   (8)

and α is the angle formed by the supplied velocity $\left({\overrightarrow{v}}_s\right)$  and the initial velocity $\left({\overrightarrow{v}}_i\right)$ .

The reasoning and the expressions (1) to (8) deduced in this section are valid for any casuistry or initial situation in which the object that intends to escape from the gravitational attraction is found (disregarding any frictional or dissipative forces). Next, we will calculate the escape velocity and the delivered velocity in various situations and casuistry of the body in question. In all the cases studied we will consider bodies that concentrate their mass at their center of gravity.

Consider a body of mass m at rest separated by a certain distance r from another more massive body of mass M Figure 1.

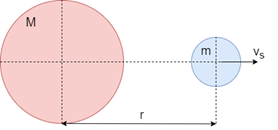
Figure 1 A body of mass m at rest at a distance r from a more massive body of mass M.

Since the body is initially at rest, the initial velocity is null ${\overrightarrow{v}}_i=0$  and the body has only potential energy at the initial instant: $E_{Pi}=-G\frac{Mm}{r}.$

Applying the expression (5) to calculate the escape velocity we have:

$v_e^2=-\frac{2}{m}\left(-G\frac{Mm}{r}\right)$   (9)

By subtracting from equation (9) the $v_e$  we obtain the expression for the escape velocity of a body at rest:

$v_e=\sqrt{2G\frac{M}{r}}$   (10)

Velocity supplied to the body at rest

Applying the expression (4) for this particular case where the body starts from rest $\left({\overrightarrow{v}}_i=0\right)$ , we have that the delivered velocity coincides with the escape velocity (10), therefore:

$v_s=v_e=\sqrt{2G\frac{M}{r}}$   (11)

Applying directly the expression (8) leads to the same result as (11).

This value corresponds to the modulus of the delivered velocity. If this velocity has radial $\left({\overrightarrow{u}}_r\right)$ and tangential $\left({\overrightarrow{u}}_t\right),$ it should be fulfilled that:

${\overrightarrow{v}}_s={\overrightarrow{v}}_{s radical} {\overrightarrow{u}}_r + {\overrightarrow{v}}_{s \tan gencial} {\overrightarrow{u}}_t$   (12)

Therefore, from (12) and (11) it follows that the modulus of should comply:

$\left|v_s\right|=\sqrt{v_{{}_{s radical}}^2+v_{{}_{s \tan gencial}}^2}=\sqrt{2G\frac{M}{r}}$   (13)

Consider a body of mass m that is allowed to fall freely from an initial distance r₀ from another more massive body of mass M and when the body is at a distance r (r < r₀) a certain energy (supplied velocity) is applied in the opposite direction of the fall so that it reaches the escape velocity (Figure 2).

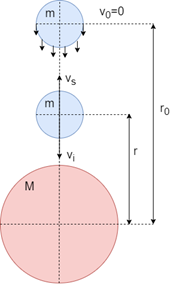
Figure 2 Body of mass m in free fall toward a more massive body of mass M.

At the initial instant at which the supplied energy is applied, the object of mass m has a certain velocity $v_r$  and is at a distance r from the massive body, so it will initially have kinetic and potential energy: $E_{Mi}=E_{ci}+E_{Pi}=\frac{1}{2}m{v}_r^2-G\frac{Mm}{r}.$

Applying the expression (5) to calculate the escape velocity we have:

$v_e^2=v_r^2-\frac{2}{m}\left(\frac{1}{2}m{v}_r^2-G\frac{Mm}{r}\right)$   (14)

Simplifying the previous expression (14) we obtain that the escape velocity for a body in free fall will be:

$v_e=\sqrt{2G\frac{M}{r}}$   (15)

Velocity supplied to the body in free fall

In this particular case the supplied velocity must go in the opposite direction to the initial velocity that is $v_r$ , in a positive radial direction, therefore, applying the expression (4) we have:

${\overrightarrow{v}}_f={\overrightarrow{v}}_e={\overrightarrow{v}}_r+{\overrightarrow{v}}_s=\left(v_s-v_r\right){\overrightarrow{u}}_r$   (16)

We calculate the modulus of ${\overrightarrow{v}}_e$  from the above expression (16):

$\left|v_e\right|=\left(v_s-v_r\right)$   (17)

Substituting the escape velocity for its previously calculated value in (15) we can obtain the value of the modulus of the delivered velocity: $v_s$

$v_s=v_r+\sqrt{2G\frac{M}{r}}$   (18)

Where $v_r$  is the velocity of the body in free fall at the previous instant to which the supplied energy is applied and can be calculated simply by conventional kinematic or energetic methods⁶ obtaining a value of $v_r=\sqrt{2G\frac{M}{r}}\left(\sqrt{\frac{r_0}{r}-1}\right).$  Therefore, substituting this value in (18) we obtain that the velocity supplied in this case should be:

$v_s=\sqrt{2G\frac{M}{r}}\left(1+\sqrt{\frac{r_0}{r}-1}\right)$   (19)

Applying directly the expression (8) leads to the same result as (19).

Consider a body of mass m orbiting circularly around another more massive body of mass M at a distance r.

With respect to the initial conditions of the body it can be shown that the orbital velocity of a body is given by³: $v_{orb}=v_i=\sqrt{G\frac{M}{r}}.$  From this definition of orbital velocity it can be deduced that the mechanical energy of a body orbiting a more massive body in circular orbit is³: $E_{Mi}=-G\frac{Mm}{2r}.$  

Therefore, applying the expression (5) to calculate the exhaust velocity we have in this case:

$v_e^2=v_i^2-\frac{2}{m}\left(-G\frac{Mm}{2r}\right)$   (20)

Substituting in (20) the initial velocity by its value shown above and simplifying the expression we obtain the escape velocity of a body in orbit:

$v_e^2=G\frac{M}{r}+G\frac{M}{r}$   (21)

$v_e=\sqrt{2G\frac{M}{r}}$   (22)

To calculate the velocity delivered to the orbiting body we will initially consider 3 possibilities: (1) that the velocity is delivered tangential to the trajectory; (2) that the velocity is delivered perpendicular to the trajectory; (3) that the velocity is delivered so that it forms a certain angle with the trajectory. In each case we will calculate the value of the delivered velocity required to reach the obtained value of the escape velocity (Figure 3).

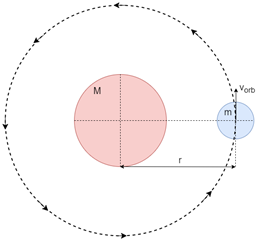
Figure 3 Body of mass m orbiting circularly at a distance r from a more massive one of mass M.

Supplied velocity tangential to the trajectory

In this case the supplied velocity will go in the same direction and sense as the initial orbital velocity that is $v_i$ , in tangential direction, therefore, applying the expression (4) we have:

${\overrightarrow{v}}_f={\overrightarrow{v}}_e={\overrightarrow{v}}_r+{\overrightarrow{v}}_s=\left(v_i+v_s\right){\overrightarrow{u}}_t$   (23)

We calculate from (23) the modulus of ${\overrightarrow{v}}_e$ :

$\left|v_e\right|=\left(v_i+v_s\right)$   (24)

Substituting the escape velocity for its previously calculated value in (22) we have:

$v_s=\sqrt{2G\frac{M}{r}}-v_i$   (25)

Since the initial velocity is the orbital velocity indicated above $\left(v_i=\sqrt{G\frac{m}{r}}\right)$ , we obtain from expression (25) a value for the supplied velocity of:

$v_s=\left(\sqrt{2}-1\right)\sqrt{G\frac{M}{r}}$   (26)

In the case where the supplied velocity was provided in the opposite direction to the initial velocity, it would be approached in the same way, only that the escape velocity would have the following expression:

${\overrightarrow{v}}_f={\overrightarrow{v}}_e={\overrightarrow{v}}_i+{\overrightarrow{v}}_s=\left(v_i+v_s\right){\overrightarrow{u}}_t$   (27)

So, obviously, a higher value of the delivered velocity would be obtained following the same procedure as shown above:

$v_s=\left(\sqrt{2}+1\right)\sqrt{G\frac{M}{r}}$   (28)

Applying directly the expression (8) we arrive at the same result in both cases, obtaining the expressions (26) and (28) (Figure 4).

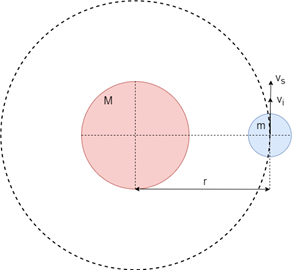
Figure 4 Velocity supplied tangential to the trajectory.

Velocity delivered perpendicular to the trajectory

In this case the supplied velocity is provided perpendicularly to the initial orbital velocity that is $v_i,$  in radial direction, therefore, applying the expression (4) we have:

${\overrightarrow{v}}_f={\overrightarrow{v}}_e={\overrightarrow{v}}_i+{\overrightarrow{v}}_s=\left(v_i{\overrightarrow{u}}_t+v_s{\overrightarrow{u}}_r\right)$   (29)

We calculate from the above equation (29) the modulus of ${\overrightarrow{v}}_e$ :

$\left|v_e\right|=\sqrt{(v_i^2+v_s^2)}$   (30)

Substituting the escape velocity (22) and the initial velocity $\left(v_i\right)$  by their value we have:

$\sqrt{2G\frac{M}{r}}=\sqrt{(G\frac{M}{r}+v_s^2)}$   (31)

By subtracting from equation (31) the supplied velocity we obtain:

$v_s=\sqrt{G\frac{M}{r}}$   (32)

Applying directly the expression (8) leads to the same result as (32) (Figure 5 & Figure 6).

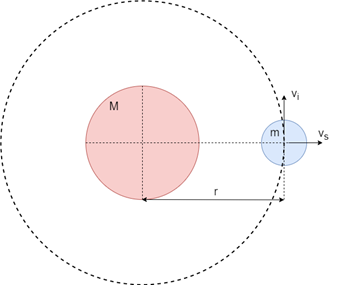
Figure 5 Velocity supplied perpendicular to the trajectory.

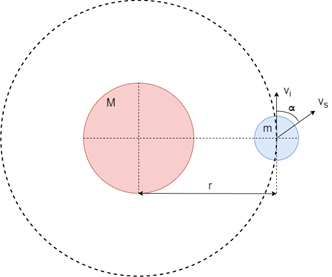
Figure 6 Velocity supplied forming an angle α with the trajectory.

Velocity delivered at an angle α to the trajectory

In this case the supplied velocity is provided forming a certain angle α with the initial orbital velocity Therefore, applying the expression (4) we have:

$\overrightarrow{v_f}=\overrightarrow{v_e}=\overrightarrow{v_i}+\overrightarrow{v_s}=((v_i+v_s\cos \alpha )\overrightarrow{u_t}+v_s\sin \alpha \overrightarrow{u_r})$   (33)

We calculate the modulus of ${\overrightarrow{v}}_e$  from the previous expression (33):

$\left|v_e\right|=\sqrt{{(v_i+v_s\cos \alpha )}^2+{(v_s\sin \alpha )}^2}$   (34)

Substituting the escape velocity (22) and the initial velocity ($v_i$  for their values we have:

$\sqrt{2G\frac{M}{r}}=\sqrt{{\left(\sqrt{G\frac{M}{r}}+v_s\cos \alpha \right)}^2+{(v_s\sin \alpha )}^2}$   (35)

We remove from the previous equation (35) the supplied velocity, obtaining:

$v_s=\sqrt{G\frac{M}{r}}(-\cos \alpha \pm \sqrt{{\cos }^2\alpha +1})$   (36)

Since we are calculating the modulus of the delivered velocity, we will always take the positive value of the above expression, since a negative modulus has no physical meaning. Therefore, from expression (36) we obtain:

$v_s=\sqrt{G\frac{M}{r}}(\sqrt{1+{\cos }^2\alpha }-\cos \alpha )$   (37)

Applying directly the expression (8) leads to the same result as (37).

It is important to note that from the expression (37) it is possible to obtain all the results of the previous sections (sections 4.1 and 4.2) for velocities delivered in different orbital situations by substituting the angle by the corresponding value in each case.

First of all, it has been observed in the previous sections that in all cases the expression of the escape velocity coincides (10), (15) y (22). This fact can be justified by alluding to the classical explanation usually used to obtain the escape velocity, which justifies that the escape velocity is that which an object must have to overcome the potential energy of a body bound to the gravitational attraction of another body (since the final mechanical energy must be zero).³ Therefore, applying the principle of conservation of energy we obtain the same expression that has been obtained in this article through the theorem of the living forces. The advantage of using the theorem of the living forces is that one can very easily distinguish the difference between the escape velocity and the supplied velocity necessary to reach that escape velocity. These two concepts are not the same and should not be confused, since the escape velocity is the velocity that a body must have to escape the gravitational attraction and the supplied velocity is the additional velocity that is provided to the object to achieve the mentioned escape velocity. That is, for a body that is at a distance r from a more massive body, the escape velocity will always be $v_e=\sqrt{2G\frac{M}{r}},$ regardless of its initial state of motion. However, the delivered velocity will depend on the initial state of the body, since the same delivered velocity will not be necessary if the body is at rest, in orbit or in free fall. Throughout the article, the value of the required delivered velocity has been obtained in several casuistry and different situations where it has been verified that, indeed, this delivered velocity is not the same in all cases (as it is the case with the escape velocity). This article has clearly shown the difference between these two concepts: escape velocity and delivered velocity, and is aimed especially at teachers and pre-university and undergraduate students so that they can delve more deeply into this subject from a rigorous point of view without conceptual errors.

None.

The author declares there is no conflict of interest.

1. Alonso Sánchez M, Martínez Salas S, Carrascosa Alís J. Estudio de la velocidad de escape: un problema planteado como investigación. Alambique: Didáctica de las ciencias experimentales. 2022;109:23–31.
2. Chinellato L, Luna Santiago Hernan, Pera, María SolIcon, et al. Clasificación de exoplanetas: desarrollo de una estrategia didáctica para abordar la construcción de modelos observacionales en Física Educativa. Latin American Journal of Physics Education. 2022;16(4):4307-1–4307-11.
3. French AP. Mecánica Newtoniana, Reverté, Barcelona, 1974.
4. Tipler PA, Mosca G. Física para la ciencia y la tecnología, Reverté, Barcelona, 2006.
5. Koppelman HH. Determination of the escape velocity of the Milky Way using a proper motion selected halo sample. Astronomy & Astrophysiscs. 2021;649:1–14.
6. Alonso M, Finn E. Física, Fondo Educativo Interamericano S.A., Buenos Aires, 1967.
7. Meriam JL. Dinámica. Reverté, Barcelona, 2000.