Entanglement dynamical features of the Jaynes-Cummings model powered through two-photon processes when the atom is driven by an external classical field while the cavity is powered initially in a coherent path. A double atomic initial case is considered, namely, initially excited atom as well as superposed one. After deriving the time evolution state of the system, the reduced density operator is derived by which von Neumann entropy; as an entanglement measure, is calculated. We show that the external classical field plays no effective role on resonance interaction as the strong coupling between the atom and field prevents all roles of any external stimulators, while on detuning interaction external pumping freezes detuning role effectively. In this case, as the external pumping becomes strong enough it forces interaction to be on an intermediate atomic level at which strong coupling between subsystems could be due again while periodical entanglement could be recovered again. Generally, these features could be noticed; but are not pronounced; when an initially superposed atom is injected into the field. Despite entropy minima of resonance case could be recovered partially, but atom-field correlations never recover purity.

Keywords: entropy, two-photon processes, classical field, detuned cavity field, coherent path

Entanglement as a pure quantum phenomenon, and due to advances in information processing field, has become the core of scientific research as it provides rich interesting applications and exciting investigations in many branches of information technology. As an important experimentally verified phenomenon, it is considered as a robust phenomena in modern physics.¹⁻³Strictly speaking, nearly all quantum communication and computation protocols⁴ provide potential applications of entanglement such as quantum teleportation,⁵⁻⁷ quantum secure direct communication,⁸ quantum computation.⁹⁻¹² Therefore, it is of great importance to quantify entanglement to assess the efficacy the quantum information processing. In this context, various proposed physical systems found the way to applications in quantum computing and quantum information processing technology.¹³⁻¹⁹ However, a great effort has been devoted in quantifying entanglement involving various methods and interesting concepts including pure or mixed state.²⁰⁻³⁰ For a pure state, von Neumann entropy is a good candidate measure.^25,31 Utilizing entropy concept, Phoenix and Knight³² noticed for the first time that, at half of the collapse time is a good measure for a pure state. It is generally believed that atoms are good candidates for storing quantum information and are natural quantum information processors. In fact, one of the simplest schemes in which entanglement can be generated is a system containing two-level atoms. Of particular interest is the interaction stimulated with two-photon processes. Due to the strong correlation between emitted photons,²⁶ two-photon interaction commonly play a very important role in atomic systems. After the discovery of Rydberg atoms, two-photon Jaynes-Cummings model (JCM) has gained a special significance due to the realization of a two-photon one-atom micromaser on Rydberg transitions in a microwave cavity.³³ Nevertheless, entanglement phenomenon is, however, still not fully understood, thus it remains as a very active research area, so, an important question that still naturally arises: how entanglement could be controlled, i.e. created, enhanced, and be robust or immune to suppression or degradation due to decoherence and dissipation resources? Although, a huge effort has been to answer this question in the past two decades but question still possessing enough mystery that should be broken in. Our proposed scheme may be a step in this direction may give a partial answer for this important question. The main target of our proposal strategy depends on exploring the role may be played -as expected- by classical pumping in controlling atom-field entanglement via two-photon processes. In fact, a very interesting and old problem in cavity QED is a two-level atom interacting with a single-cavity mode via two-photon processes and have been explored extensively from various view points. To the best of our knowledge, a problem of entanglement of a classically two-level atom powered by two-photon processes has not been broken through. Although generalization from one- two two-photon processes mediated by classical pumping seems simple, but, in fact, it contains many complications in details. Indeed, entanglement generation through field assisted by continuous external pumping seems not an old problem.³⁴⁻³⁶ However, entanglement dynamics and purity of a two-level atom driven by a classical field, and interacting with a coherent field in a dissipative environment have been investigated.³⁷ Thus, the past two decades carried many investigations and proposals that have been established in studying of coupled atom and field assisted by continuous external pumping.^27,28,34-36 An outline of our paper is as follows: In Sec.II, we describe the model Hamiltonian including the initial settings of both atom and field, then, through the solution of Schrodinger equation, we insert short remarks about the procedure we are following to solve it for that system to obtain the time evolution wave function. In Sec.III, we derive the reduced density operator for the atomic subsystem followed by a short introduction about von Neumann entropy; the entanglement measure we are intending to use for quantifying degree of entanglement between the field and atom. A detailed discussion of the numerical findings is presented in Sec.IV, while our conclusion is written down in Sec.V.

Model hamiltonian and total system wave function

The starting point in our strategy is the Hamiltonian description of a two-level atom interacting with two fields, one is quantum while the other is classical, namely a classically driven two-photon JCM. In the rotating wave approximation, system Hamiltonian is expressed as, (setting k =1)

$\widehat{V}\left({\widehat{f}}^{†}f,t\right)=\widehat{V_{}{}_0}\left({\widehat{f}}^{†}f\right)+\widehat{V_{}{}_I}\left({\widehat{f}}^{†}f,t\right)$       (1)

With

$\widehat{V_0}\left({\widehat{f}}^{†}f\right)={\omega }_f{\widehat{f}}^{†}\widehat{f}+{\omega }_a\widehat{{\pi }_z}$      (2)

$\widehat{V_0}\left({\widehat{f}}^{†}f,t\right)=\lambda \left(\widehat{{\pi }_{+}}{\widehat{f}}^{†2}+\widehat{{\pi }_{-}}{\widehat{f}}^2\right)+\left[\varpi \widehat{{\pi }_{+}}\exp (2i{\omega }_{l}t)+{\varpi }^{*}\widehat{{\pi }_{-}}\exp (2i{\omega }_{l}t)\right]$                 (3)

where ${\omega }_a$ (ωf ) is atomic (field) frequency, while ${\hat{f}}^{†}\hat{f}=\hat{n}$ is the quantum number expressed in terms of the annihilation (creation) operator$\widehat{f}({\widehat{f}}^{†})$ satisfying the commutation relation $\left[\widehat{f},{\widehat{f}}^{†}\right]=1$ . The notation ${\hat{\pi }}_{+}\left({\hat{\pi }}_{-}\right)$and ${\hat{\pi }}_z$ represent, respectively the raising (lowering) and population operators of the atom, while λ is the coupling constant between the atom and the cavity field mode , is the coupling constant between atom and the external classical of frequency ${\omega }_l$ . Generally ${\omega }_a,{\omega }_{f}and{\omega }_l$ are different. However, our solution strategy needs the Hamiltonian Eq.(1) to be simplified which may be accomplished utilizing the rotating frame technique which allows us to write the Hamiltonian Eq.(1) as (assuming $\varpi$ as real)

${\hat{V}}_{eff}({\hat{f}}^{†}f,t)=△{\hat{\pi }}_z+\lambda ({\hat{\pi }}_{+}{\hat{f}}^{†2}+{\hat{\pi }}_{-}{\hat{f}}^2)+\varpi [{\hat{\pi }}_{+}+{\hat{\pi }}_{-}]$                 (4)

Actually, the external driving frequency ${\omega }_l$ is supposed to be significantly different from atomic frequency ${\omega }_a$ and field frequency ${\omega }_f,$ but for simplicity, we take it the same as cavity frequency ${\omega }_f,$ namely, ${\omega }_f={\omega }_l,$ this allows us to write the detuning parameter as $\Delta = \left({\omega }_{a }-{\omega }_l\right) = \left({\omega }_{a }-\omega f\right)$ . Our next step is the simplification of the Hamiltonian Eq.(4) further, however, the simplification could be achieved using the Glauber displacement operator $D\left(\zeta \right)=\exp \left(\zeta f^{+}-{\zeta }^{*}f\right)$ with $\zeta =\varpi /\lambda$ which produces a final form of Eq.(4) as

with${\hat{V}}_{eff}({\hat{f}}^{†}f,t)=D^{†}\left(\zeta \right)[\Delta {\hat{\pi }}_z+\lambda ({\hat{\pi }}_{+}{\hat{f}}^{†2}+{\hat{\pi }}_{-}{\hat{f}}^2)]D\left(\zeta \right)=D^{+}\left(\zeta \right){\hat{V}}_{eff}({\hat{f}}^{†}f,t)D\left(\zeta \right)$      (5)

${\hat{V}}_{eff}({\hat{f}}^{†}f,t)=D\left(\zeta \right){\hat{V}}_{eff}({\hat{f}}^{†}f,t)D^{†}\left(\zeta \right)$       (6)

With aid of the final form of our simplified Hamiltonian Eq.(6) while assuming that the interaction is initially operated along a coherent path;$|{\psi }_F\left(0\right)\rangle =|\alpha \rangle ,$ and with the assumption that the atom is in a state of superposition $|{\psi }_A\left(0\right)\rangle =X|e\rangle +Y|g\rangle ,$ where ${\left|X\right|}^2+{\left|Y\right|}^2$ , the solution of the Schrodinger

$i\frac{d}{dt}|\tilde{\psi }⟩={\hat{V}}_{eff}({\hat{f}}^{†}f,t)|\tilde{\psi }⟩,$                (7)

taking into consideration that $|\tilde{\psi }⟩=D^{†}\left(\zeta \right)|\psi ⟩,$yields the wave function of the total system as

$|\tilde{\psi }(t)\rangle ={\displaystyle \sum _n{q}_n}\left[X\left(A\left(n,t\right)|-\zeta ,n,e\rangle +B(n,t)|-\zeta ,n+2,g\rangle \right)+Y\left(A^{*}\left(n-2,t\right)|-\zeta ,n,g\rangle +B(n-2,t)|-\zeta ,n-2,e\rangle \right)\right],$ (8)

with $\zeta =\varpi /\lambda$ where $q_n=\exp \left(-\frac{\left|\zeta +{\alpha }^2\right|}{2}\right)\frac{{\left(\zeta +\alpha \right)}^{n/2}}{\sqrt{n}!},$ and the quantities X and Y are the coefficients of the atomic superposition with X = cos θ and $Y=e^{i\varphi }\sin \theta ,$ where θ and $\varphi$ represent, respectively, The degree of excitation and the relative phase. The probability amplitudes A∗(n, t) and B(n, t) may be expressed as$A_n\left(t\right)=\cos \left(f_{n}t\right)-i\frac{\Delta }{2}\frac{\sin (f_{n}t)}{f_n},$ (9)

$B_n\left(t\right)=-i\lambda \sqrt{\left(n+1\right)\left(n+2\right)}\frac{\sin (f_{n}t)}{f_n},$ (10)

$f_n=\sqrt{\frac{{\Delta }^2}{4}+{\lambda }^2\left(n+1\right)\left(n+2\right)}$ (11)

Reduced density operator and quantum entropy

With the wave function $|\psi \left(t\right)\rangle$ has been calculated, any property related to the atom or the field can be calculated. The reduced density operators can be obtained through tracing over the vector

product $|\psi \left(t\right)\rangle \langle \psi \left|t\right||,$ namely,

${\rho }_{a(f)}(t)=T_r|\psi \left(t\right)\rangle \langle \psi \left|t\right||,$     (12)

and we have used the subscript a(f ) to denote the atom(field). We should note here that if the atom-field system is initially in pure state, then at t > 0, the entropies of the field and the atomic subsystems are precisely equal.

Using the wave function obtained, Eq.(8), one can easily gets the vector ψ(t) ψ(t) , over which tracing the field variables, the reduced density matrix of the atomic subsystem, is then, takes the form,

${\rho }^a(t)={\displaystyle \sum _{i,j=1}^2{\rho }_{i,j}}(t)|i\rangle \langle j|,$ (13)

where

$\begin{array}{l}{\rho }_{11}(t)={\displaystyle \sum _n{\left|q_n\right|}^2{\cos }^2(\theta ){\left|A_n(t)\right|}^2+}{\displaystyle \sum _n{\left|q_{n+2}\right|}^2{\sin }^2(\theta ){\left|B_n(t)\right|}^2}\\ +\frac{\sin (2\theta )}{2}{\displaystyle \sum _n{q}_n^{*}{q}_{n+2}}(exp(i\varphi )B_n(t)A_n^{*}(t)+exp(-i\varphi )B_n^{*}(t)A_n^{*}(t))\end{array}$ (14)

$\begin{array}{l}{\rho }_{12}(t)={\displaystyle \sum _n{q}_n{q}^{*}co{s}^2(\theta )A_n(t)B_{n-2}^{*}(t)+}\frac{1}{2}{\displaystyle \sum _n{\left|q_n\right|}^2}exp(-i\varphi )sin(2\theta )A_n(t)A_{n-2}(t)\\ +\frac{1}{2}{\displaystyle \sum _n{q}_n{q}_{{}_{n-4}}^{*}}exp(i\varphi )sin(2\theta )B_{n-2}(t)B_{n-4}^{*}(t)+{\displaystyle \sum _n{q}_n{q}_{{}_{n-2}}^{*}}si{n}^2(\theta )B_{n-2}(t)A_{n-4}^{}(t)={\rho }_{21}^{*}\end{array}$ (15)

$\begin{array}{l}{\rho }_{22}(t)={\displaystyle \sum _n{\left|q_n\right|}^{2}co{s}^2(\theta ){\left|B_{n-2}^{}(t)\right|}^2+}{\displaystyle \sum _n{\left|q_{n+2}\right|}^2}si{n}^2(\theta ){\left|A_n\right|}^2(t)\\ +\frac{\sin (2\theta )}{2}{\displaystyle \sum _n{q}_n^{*}{q}_{n+2}}(exp(i\varphi )A_n^{*}(t)B_n^{*}(t)+exp(-i\varphi )A_n^{}(t)B_n^{}(t))\end{array}$ (16)

Up to this stage, we are at the position to compute analytically entanglement measure between the atom and field. For bipartite systems being prepared initially in a pure state, several methods for measuring degree of entanglement including, for example, Shannon entropy,³⁸ Renyi entropy,³⁹ Tsallis entropy,⁴⁰ linear entropy,^41,42 entanglement of formation²⁵ and the von-Neumann entropy.³¹ Indeed, among these methods of measurements the most common choice of entanglement measure, as has been mentioned above, is the von-Neumann entropy of the reduced density matrices ${\rho }_A$ or ${\rho }_B$

$S\left({\rho }_{A(B)}\right)=-T_r\left({\rho }_{A(B)}\ln {\rho }_{A(B)}\right)$      (17)

Depending on the initial state of the whole system, explicit numerical simulation of the results of the elements in Eq.(13) can be calculated. Tracing over the field variables, von Neumann entropy between the atom and the field is given by

$S_F(t)=-{\displaystyle \sum _{s=1}^2{\eta }_s}\ln {\eta }_s(t),$            (18)

where ${\eta }_{1,2}(t)$ , are the roots of quadratic ordinary differential equation resulted from the determinant

| $\left|{\rho }^a\left(t\right)-\eta I\right|=0$       (19)

with I is the unity matrix.

Indeed, we now are in a position to picture numerically the above analytically obtained results; however, the next section will be devoted for discussion and analysis of the obtained numerical results.

Based on the analytical mathematical formulae presented above, dynamics of the field entropy as a function of the normalized scaled time λt/π will be pictured and, in detail, analyzed. For purposes of comparison, double criteria will be taken into consideration, namely, the standard two-photon JCM with an initially excited atom while the other will be with an initially superposed one, shining light, specially, on the role of the classical pumping and how/or to what extent can classical pumping affects degree of entanglement between the subsystems. For all our plots, we will preserve a fixed mean photon number $\langle n\rangle$ as $\overline{n}=25$ . Our first criterion is shown in Figure 1a, where the dynamics of the well known evolution of von Neumann entropy of the standard two-photon JCM,²⁰ where entropy is a periodic function of time at the half of the revival time the field entropy reaches its maximum. In this case, the term ρ₁₂ appears in the reduced density operator eigenvalues Eq.(13) that responsible for interference effects has no any effective contributions. In such a case, contributions on SF just come from ρ₁₁ and ρ₂₂, due to invariance of the Hamiltonian V ; Eq.(1), caused by its symmetries that carried in ${\hat{\pi }}_{\pm }={\hat{\pi }}_x+i{\hat{\pi }}_y$operators. In other words, depending spin reflection of x or y components, spin states parities change mutually, the spin states can be classified accordingly. Consequently, as the parity remains conserved due to the symmetry, the opposite-parity states never get mixed through time development caused by V , thus contributions from ρ12 vanish. Thus, entropy S_F (t) evolves periodically at periods $\pi /\lambda$ , when $\lambda t=n\pi \left(n=0,1,2,3,\mathrm{...}\right),$ to the minimum values and the field is completely disentangled from the atom, while when $\lambda t=\left(n+\frac{1}{2}\right)\pi$ the field entropy evolves to the maximum value and the field is strongly entangled with the atom. In other words, as it has been stated by Phoenix and Knight,³² at the half-revival time the atom and field become appreciably separable, otherwise correlations between them dominates. Moreover, as a consequence of separability, cavity Schr¨odinger cat state will be generated, namely, the cavity is in a coherent superposition of the two opposite-phase states. In fact, such a result has been experimentally realized.⁴³ Worthy noting that, Poissonian initial coherent state will be bifurcated into two parts in phase space, which at on separability they differ by an angle π. For well understanding, the effects of different frequency widths between the atom and field in absence of classical pumping will be examined. Ranging from relatively small to relatively big frequency differences, i.e, δ=10, 20, 30 and δ=40, these effects will be traced and analyzed. Temporal snapshots, respectively, are displayed in Figures 1b−1e. Actually, as well as detuning parameter δ takes a considerable higher value, periodicity is broken in while rapid Rabi oscillations begin to appear between quasi periods (Figure 1c). Another important notice is that, the later the normalized scaled time, the lower the entropy minima can be obtained. Increasing δ further resulted in an interesting observations, entropy SF dips and peaks sinusoidally with time without normal collapses and revivals Figure 1d & 1e. Also, entropy first maximum fall remarkably while its first minimum occurs later. Furthermore, as bigger as the detuning is, Rabi oscillations become more and more dense. Additionally, while δ is increased, the area that Rabi oscillations occupies becomes wider. Worth noting that entropy minima become more and more lower while the chance for entropy to fall to zero totally vanishes, in other words, entropy still survive at all instants of the normalized scaled time.

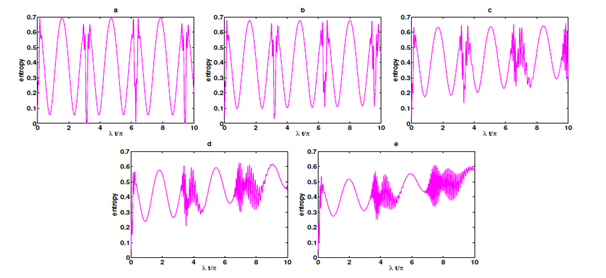
Figure 1 Entropy SF (t) dynamical evolution against the normalized time $\lambda t/\pi$ when$\phi =0, \theta =0, \overline{n}=25, \zeta =0$ , where $a:\delta =0;b:\delta =10;c:\delta =20,d:\delta =30ande:\delta =40.$ .

The effect of the weak strength of classical pumping where different values of detuning are used is depicted in Figure 2. For both resonance interaction and relatively small detuning, there is no important observations could be mentioned, compare (Figure 1a, 1b, 2a & 2b). Nevertheless, switching classical pumping even with weak strength reduces Rabi oscillations density as well as increasing minima values of entropy, compare (Figure1c and 2c). Preserving general behaviors as in previous case, the presence of classical pumping while detuning δ increased not only increasing entropy minima but also entropy maxima raised noticeably, compare (Figure1d, 1e, 2d & 2e). However, entropy still survives at all instants of the normalized scale time and the chance to fall to zero completely vanishes. Additional important effect is that, while in previous case sinusoidal peaks broaden, the presence of classical pumping resulted in peaks narrowing here, in other words, while confinement on sinusoidal behavior suffering from atrophy in absence of classical pumping, the presence of classical pumping resulted in improvement of confinement condition where rapid sinusoidal behavior could be noticed, namely, more peaks could appear in the same interval of the normalized scaled them, compare Figure 1d, 1e, 2d & 1e.

Before we proceed, worthy noting that, in resonance case, regardless of classical pumping strengths, global periodic behavior of entropy SF is preserved, this is due to the contributions of classical pumping limited to the quantum photon number distribution qn 2. Although the highest degree of entanglement has not been reached under the considered conditions,²⁶ but increasing pumping strength further and further resulted in both entropy maxima and minima increase will due again gradually to the extent that on a case of super pumping strength we could obtain an entropy behavior resembles so far the resonance case, see Figure 3d, 3e, 4d, 4e, 5d & 5e), in other words, the four series of disentanglement times are totally disappear while entropy still evolves strictly periodic. Nevertheless, one important difference can be noticed clearly where that regions occupied by Rabi oscillations are reduced gradually by increasing classical pumping power. This is actually conflicts with the fact that, when δ seems big, the coupling between atom and the field becomes noticeably weak, thus atom and field exhibit lower degree of entanglement. Indeed, an explanation of this mysterious behavior becomes duty here. An interpretation is found beyond the effective effect of classical pumping that provides the whole system with an additional effective energy momentum that helps in tunnelling through this kind of coupling suppression.

Figure 2 The same as Figure 1 but for $\zeta =0.875$ .

Figure 3 The same as Figure1 but for $\zeta =1.75$ .

Figure 4 The same as Figure 1 but for $\zeta =2.75$ .

Figure 5 The same as Figure 1 but for $\zeta =3.75$ .

In this part of discussion, we answer the important question: What about the shape of correlations between the subsystems, namely, the atom and field, if an initially superposed atom is injected into the field? A detailed answer can be caught from figures.⁶⁻¹⁰ At begin, it noteworthy that the results are obviously different from the case that atom is injected into the cavity initially in an excited state. For a purpose of comparison, our starting point will be from Figure 6 of the case where no classical pumping is present. On resonance situation, entropy SF evolves periodically with behavior looks like two photon population inversion²⁰ but with sinusoidal collapses Figure 6a. However, nothing new could be noticed compared to what was seen before in case of initially excited atom concerning development periods. Nevertheless, globally, the behavior carries an important difference where entropy minima and maxima are [0.05, 0.125] while it reaches instantaneous minima and maxima per a double periods of the normalized time scale. Indeed, in this case the contributions of the coherence term ρ₁₂ vanishes taking into consideration the effect of the initial injection of the superposed atomic states that contributes passively on entropy temporal evolution. It is argued that⁴⁴ for a coherent superposition, to be applicable, needs to have large enough amplitude. In other words, the more structures of coherent states superposition with higher amplitudes, hence, higher photon numbers are employed. With the gradual increase of detuning δ, the regular periodical behavior of entropy is distorted gradually while regions occupied by Rabi oscillations spread notice- ably that resulted in shifting sinusoidal collapses remarkably to the right (Figure 6b). Moreover, entropy maxima are raised as time passes accompanied with reducing its local minima.

If the classical pumping strength is increased to super strength, an interesting behavior of super revivals or revival of revivals occurs at longer times after one period of sinusoidal collapse. We should also mention that the entropy at the revival time significantly decreases with an increase of the detuning and for larger detuning the subsystems become obviously less entangled, compare (Figure 6c, 6e & 6d). In other words, the field carries the lower possible momentum and is less coupled to atom. Note although entropy remains oscillating around first maximum, however, SF maxima increase gradually to reach possible maximum at end of scaled time. Additionally, Rabi oscillations intervals considerably spread and their minima noticeably squeezed (Figure 6e). In other words, subsystems spend longer times relatively strong entangled while entropy remains survive during the whole normalized time scale and subsystems never recover purity again. Worth noting that, quasi periods shifted to right considerably where the first local minimum appears later than before.

Findings on switching weak pumping strength are depicted in Figure 7. Generally, the presence of classical pumps affects SF global behavior passively where entropy first maxima seem remarkably lower than previous case. Despite the negative effect resulting from injection of initially superposed atom, classical pumping still possessing its effective role in providing the system with and additional effective energy momentum where both entropy minima and maxima spreads clearly along the vertical axis, (Figure 7b). Increasing detuning in coexistence of a weak classical pumping diminishes Rabi oscillations regions while quasi periods shifted to left noticeably, see (Figure 6d, 6e & 7d, 7e). In other words, the time at which the atom and field exchange energy rapidly becomes earlier than before. Further, the gradual raise of entropy towards the possible maximum at end of normalized time scale occurs slower than that one noticed before; compare Figure 6b, 6c & 7b, 7c).

On increasing classical pumping strength further, many interesting phenomena are born and clearly noticed. First, the gradual grow in entropy towards the possible maxima at end of normalized time scale occurs more slowly compare (Figure 7c & 8c). Second, Rabi oscillations show super revivals or revival of revival while sinusoidal peaks squeezed remarkably. An ideal resemblance to the case of resonance could be obtained as soon as classical pumping power reaches it super strength (Figure 9 & 10). An important notice is the remarkable growth in entropy maxima when a super power of classical pumping may be used.

Figure 6 The same as Figure 1 but for $\theta =\pi /4$ .

Entanglement between a single two-level atom and a detuned electromagnetic field has been studied while the atom is classically pumped. The wave function controlling system temporal evolution has been obtained in an analytical form. Two initial atomic states have been considered, namely, initially excited atom as well as initially superposed one. Through the calculation of the reduced density operator, von Neumann entropy has been calculated and numerically analyzed shining light especially onto the effective role of the classical pumping. Various strengths of the driving classical field have been examined starting from a weak pumping strength through a super pumping one when the frequency difference between the atom and the field changes from resonance through the possible wider frequency difference. Findings pointed out that on the resonance interaction, the classical pumping plays no any effective role due to strong coupling between the atom and the field which freezes pumping efficiency, in other words, prevents penetration of any other additional stimulators. On detuned interaction classical pumping plays a very effective role. Nevertheless, classically pumping effectiveness seems highly pronounced when we start interaction with initially excited atom. Moreover, it was apparent that, on detuned interaction, classical pumping plays a very efficient role, where it suppressed detuning effectiveness considerably. Regardless of the obtainable entanglement is rather low on weak pumping but in that situation classical pumping forcing interaction to be on an intermediate atomic level at which atom-field coupling stimulated strongly by classical pumping strength where under certain super strengths strong entanglement could be recovered. A very important result is that, although the shape of atom-field entanglement recovers a kind of resonance entanglement but subsystems couldn’t recover purity again. From the above we can conclude that the resonant quantum dynamics not permanently leads to a strong entanglement between subsystems, but adjusting detuning difference and pumping strengths interaction can lead to more significant entanglement regardless of the first stage of time evolution.

None.

The authors declare that there is no conflicts of interest.

1. Peres A. Quantum Theory: Concepts and Methods, Kluwer Academic Publisher, The Netherlands; 1995.
2. Auffeves A, Maioli P, Meunier T, et al. Entanglement of a Mesoscopic Field with an Atom Induced by Photon Graininess in a Cavity. Phys Rev Lett. 2003;91:230405.
3. Matsukevich DN, Chanelire T, Jenkins SD, et al. Entanglement of Remote Atomic Qubits. Phys Rev Lett. 2006;96:030405.
4. Nielsen MA, Chuang IL. Quantum Computation and Quantum Information. Cambridge University Press, Cambridge; 2000.
5. Ekert A, Zeilinger. The physics of Quantum information: Quantum Cryptography, Quantum Teleportation, Quantum Computing. Boumeester, editor. Springer, Berlin; 2000.
6. Bennett CH, Brassard G, Cr´epeau C, et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys Rev Lett. 1993;70.
7. Bouwmeester D, Pan JW, Mattle K, et al. Nature. 1997;390:575.
8. Marzolino U, Buchleitner A. Quantum teleportation with identical particles. Phys Rev. 2015;91:032316.
9. Gruska J. Quantum Computing. McGraw-Hill, 1999.
10. Machhiavello C, Palma GM, Zeilinger Z. Quantum Computation and Quantum Information Theory. World Scientific New Jersey, 2000.
11. Bennett CH, DiVincenzo DP. Nature. 2000.
12. Deng FG, Long GL, Liu XS. Phys Rev. 2003;A68:042317.
13. Barenco A, Deutsch D, Ekert A, et al. Conditional Quantum Dynamics and Logic Gates. Phys Rev Lett. 1995;74:4083.
14. Vandersypen LMK, Steffen M, Breyta G, et al. Nature. 2001.
15. Chuang IL, Gershenfeld N, Kubinec M. Phys Rev Lett. 1998;80:3408.
16. Jones JA, Mosca M, Hansen RH. Nature. 1998.
17. Cirac JI, Zoller P, Itano WM. Demonstration of a Fundamental Quantum Logic Gate. Phys Rev Lett. 1995;74:4714.
18. Turchette QA, Hood CJ, Lange W. Measurement of Conditional Phase Shifts for Quantum Logic. Phys Rev Lett. 1995;75:4710.
19. Alexander Shnirman, Gerd Schön, Ziv Hermon G. Quantum Manipulations of Small Josephson Junctions. Phys Rev Lett. 1997;79:2371.
20. Abdel-Aty M, Furuichi S, Ateto M. Japan. J App Phys. 2002;41(1):111.
21. Boukobza E, Tannor DJ. Thermodynamic analysis of quantum light amplification. Tannor Phys Rev. 2005;A74:063821.
22. Ateto MS. An investigation of a nonlocal entanglement of two uncoupled atoms embedded in a coherent cavity field and the associated phase space distribution: one quantum nonlinear process. Int J Quant Inf. 2007;8(6):1045−1073.
23. Akhtarshenas SJ, Farsi M. Negativity as entanglement degree of the Jaynes–Cummings model. Phys Scr. 2007;75(5):608.
24. Ateto MS. Control of a Nonlocal Entanglement in the Micromaser via Two Quanta Non-Linear Processes Induced by Dynamic Stark Shift. Int J Theor Phys. 2009;48:545.
25. Ateto MS. Quantum Entropy of a Nonlinear Two-level Atom with Atomic Motion. Int J Theor Phys. 2010;49(2):276−292.
26. Bashkirov EK. Entanglement in the degenerate two-photon Tavis–Cummings model. Physica Scripta. 2010;82(1):015401.
27. Ateto MS Entanglement Dynamics and Spin Squeezing of The non-linear Tavis-Cummings model mediated by a Nonlinear Binomial Field. Int J Quant Inf. 2015;13(5):1550034.
28. Ateto MS. Quantum Inf Process. 2017;16:267.
29. Baghshahi HR, Tavassoly MK, Akhtarshenas SJ. Quantum Inf Process. 2015;14:1279.
30. Ateto MS, Abo-Kahla DAM, Abu-Alhamed SF. 7th International Conference on Mathematics and Information Sciences. 2018;15−17.
31. J. von Neumann, The Mathematical Foundations of Quantum Mechanics (Princeton University Press, Princeton, 1955).
32. Simon JD Phoenix, Knight PL. Establishment of an entangled atom-field state in the Jaynes-Cummings model. Phys Rev. 1991;44:6023.
33. Brune M, Raimond JM, Goy P. Quantum switches and nonlocal microwave fields. Phys Rev Lett. 1993;71:2360.
34. SolanoE, Agarwal GS, Walther H. Strong-Driving-Assisted Multipartite Entanglement in Cavity QED. Phys Rev Lett. 2003;90:027903.
35. Akhtarshenas SJ, Khezrian M. Entanglement dynamics and decoherence of an atom coupled to a dissipative cavity field. Eur Phys J. 2010;57(2010):271.
36. Burlak G, Starostenko O, Hernandez JA. Rev Mex Fis. 2006;52(3):213.
37. Zhang JS, Xu JB. Optics Communications. 2009;282:2543.
38. Shannon CE. A Mathematical Theory of Communication. Bell Syst Tech J. 1948;27:379.
39. R´enyi A, Fourth Berkeley Symp. Math Stat and Probability. Berkeley, CA: University of California Press.;1961:547−561.
40. Tsallis C. Possible Generalization of Boltzmann-Gibbs Statistics. J Statist Phys. 1988;52(1):479.
41. Zurek WH, Habib S, Paz JP. Linear entropy in quantum phase space. Phys Rev Lett. 1993;70:1187.
42. Laura EC, Rosales-Zarate, Drummond. Phys Rev. 2011;A84:042114.
43. Haroche S, Raimond. Exploring the Quantum. Atoms, Cavities and Photons. New York: Oxford University Press. 2006.
44. Yukawa M, Miyata K, Mizuta T, et al. Generating superposition of up-to three photons for continuous variable quantum information processing. 2013;5529.