Twenty20 format of cricket is a fast track ball game compared to the other formats of cricket viz. Test and One-day International (50-over a side). The Indian Premier League (IPL) is a national franchise based Twenty20 cricket tournament initiated by Board of Control for Cricket in India (BCCI). In this format, each batsman tries to score maximum runs in minimum balls. This fact increases the probability of dismissal of a batsman. As fall of wickets leads to the loss of resources of the batting side, thus it has an impact on the result of the game. This study tries to examine the survival ability of Indian and overseas batsmen in IPL 2012 season using a probabilistic model. The proposed model can be used to forecast the survival rate of the batsmen on the pitch in other format of cricket also, while the game is in progress. The findings of the study can be used to arrange the batting order of a team in Twenty20 cricket based on the match situation.

Keywords: cricket, probability, survival analysis, sport

Cricket is an outdoor game played between two teams of eleven (11) players each in a circular ground. It is administered by certain rules and regulations, where the interaction between bat and ball takes place on a 22-yard hard surface in the middle of a circular ground called the cricket pitch. Unlike other sports, there are different versions of cricket. The different versions of cricket can be broadly classified as unlimited overs cricket (Test matches) and limited overs cricket (One-day and Twenty20). Indian Premier League (IPL) is a national franchise based Twenty20 format of cricket league initiated by Board of Control for Cricket in India (BCCI) in 2008. In IPL, each team faces only twenty (20) overs in a match, therefore, within these limited overs every batsman tries to score maximum runs in minimum balls. In the process of scoring runs quickly, the batsmen are exposed to the risk of losing their wicket. This fact increases the probability of dismissal of a batsman. As fall of wickets leads to the loss of resources of the batting side, so it has an impact on the result of the game. However, it does not mean that stability of a batsman on the pitch would help a team to win the match. Evidently, he should have scored runs as quickly as possible. Thus, in Twenty20 cricket, one can atleast measure how much time a batsman can survive or how many balls a batsman can face on the cricket pitch while batting. Therefore, the study makes an attempt to measure as well as compare the standing capability of Indian and overseas batsmen on the cricket pitch in IPL 2012 using survival analysis.

Survival analysis is defined as a set of methods for analyzing data where the outcome variable is the time until the occurrence of a particular event of interest.¹ The event could be death due to cancer, occurrence of a disease, relief from a severe back pain, etc. Let us take an example to explain mathematical definition of survival function. Suppose the actual survival time of an individual (say) t which can be regarded as the value of a variable T (i.e. associated with the survival time). It can take any non-negative value. The different values that T can take have a probability distribution, so the variable T can be considered as a random variable. Now for the random variable T, the probability distribution function of T can be defined as F(t) and it is given by

$F(t)=P(T<t)={\displaystyle \underset{0}{\overset{t}{\int }}f(x)dx}$      (1)

Which represents the probability that the survival time is less than some value t. Now the survival function is defined as the probability that the survival time is greater than or equal to t. Usually, it is denoted by S(t) and given by

$S(t)=P(T\ge t)\Rightarrow 1-P(T<t)\Rightarrow 1-F(t)\Rightarrow 1-{\displaystyle \underset{0}{\overset{t}{\int }}f(x)dx}$      (2)

Therefore, the survival function can be used to represent the probability that an individual survives from the time origin to some time beyond t. The survival time or time to an event of interest can be measured in days, weeks, years, etc. in which the objects or subjects are followed over a specified period of time to pinpoint the event of interest occurs. Though its uses in medical, clinical trial, actuarial science, etc. are hefty, but still the application of survival analysis in sport (especially in cricket) is limited. A few studies have found in this regard are explicitly mentioned here. Danaher² applied the survival analysis to find an estimate of a cricketer’s unknown batting average³ based on the product limit estimator. Similar product-limit estimation technique was adopted by Kimber and Hansford³ for assessing the batting performance of cricketers based on runs scored. The product limit estimator (PLE) is a non-parametric estimator originally proposed by Kaplan and Meier⁴ and it is defined as -

$PLE={\displaystyle \prod _{t_i\langle t}\left(1-\frac{d_i}{n_i}\right)}$ , $t_1 t_2 t_3 \dots t_n$      (3)

Where t_i be the observed times of n samples until the event of interest occurred from a given population. However, sometimes lack of information arises when observations have some information available for the event of interest but the information is not complete. This incomplete information is termed as censoring. If there is no censoring, n_i is the number of survivors prior to time t_i. But if there is a censoring, n_i is the number of survivors minus the number of censored cases in the sample. To measure the survival capability of cricketers on the cricket pitch, censoring can be perceived in those situations when a batsman remains not-out in limited overs cricket. It can be termed as so-called right censoring data.

Following the work of Kimber and Hansford,⁴ product limit estimator was used by Das⁶ to estimate the adjusted batting average of some selected cricketers. He argues, it has been revealed from the past information that batsmen have a variable risk of getting dismissed based on their current score in the innings. Thus, he proposed to model the batsmen’s scores using generalized geometric distribution. A similar problem was also addressed by van Staden⁷ developing a new batting criterion named as ‘survival rate’. It is defined as the number of balls faced in all innings divided by the number of completed innings. Symbolically,

$SV=\frac{Numberofballsfaced}{Numberofcompletedinnings}=\frac{1}{n}\left({\displaystyle \sum _{i=1}^n{b}_i}+{\displaystyle \sum _{i=n+1}^{n+m}{b}_i^{*}}\right)$      (4)

where b_i (i = 1, 2, … , n) represents the number of balls faced by the batsman in n completed innings and (i = n+1, n+2, …, n+m) represents the number of balls faced by the batsman in (n+m) not-out innings. Now on the basis of equation (2) and the batting average developed by Maini and Narayanan (2007) which is based on average exposure-to-risk (AV_exposure), van Staden et al (2010) proposed a new meaningful batting average. It is based upon exposure using survival rate and it is defined as

$A{V}_{survival}=\frac{SV}{A{V}_{\exp osure}}$

Where $A{V}_{\exp osure}=\frac{{\displaystyle \sum _{i=1}^n{x}_i}+{\displaystyle \sum _{i=n+1}^{n+m}{x}_i^{*}}}{{\displaystyle \sum _{i=1}^n{r}_i}+{\displaystyle \sum _{i=n+1}^{n+m}{r}_i^{*}}}$      (5)

Where $r_1,r_2,\mathrm{...},r_n$  and $r_{n+1}^{*},r_{n+2}^{*},\mathrm{...},r_{n+m}^{*}$  denote the batsman’s exposure in n completed innings and m not-out innings respectively. Here, $r_i=1$ if the score in i^th innings is a completed score, which means that, the exposure is one for all completed innings.

Otherwise,  $r_i^{*}=\{\begin{array}{l}{b}_i^{*}/\overline{b},ifthescoreisanot-outscoreand{b}_i^{*}<\overline{b}\\ 1,else\end{array}$

Where $\overline{b}$ is the average number of balls faced by a batsman in his (m+n) innings and it is defined as,

$\overline{b}=\frac{Numberofballsfaced}{Numberofinnings}=\frac{1}{n+m}\left({\displaystyle \sum _{i=1}^n{b}_i}+{\displaystyle \sum _{i=n+1}^{n+m}{b}_i^{*}}\right)$

At this point, it is very crucial to clarify that the word ‘survival rate’ stands here to exemplify the capability of a batsman to remain present on the cricket pitch during a match. So that there will be no confusion with the measure defined by van Staden⁷ (c.f. equation (4)). When we mentioned the word “survival” in terms of batsman in cricket, it could be the end of the time spent by a batsman on the pitch before dismissal. As mentioned earlier, time to an event of interest can be measured in days, weeks, etc. Similarly, a batsman’s ability to stand on the pitch in the match(es) can be measured in terms of number of balls faced by him. It can be considered as an outcome variable in so-called survival analysis. Thus, if a batsman has been facing consistently colossal number of balls in the match(es) then he would have the higher probability of survival on the pitch.

The approach of this study is different than earlier studies, as it does not focus on any single performance statistics of batsman like batting average, strike rate, etc. Instead, a non-parametric estimator established by Kaplan and Meier (1958) a long back is used to calculate survival probability of batsman on the pitch based on the information of number of balls faced as well as whether the player was out or not-out in the match(es). The methodology applied here is discussed below in details. Let O_i = 1, if a batsman out in the i^th ball of a match and 0 otherwise, n_i be the number of batsmen survives prior to b_i balls of a match, where b_i is the observed number of balls faced by the batsmen in a match. However, as mentioned earlier, to measure the survival capability of batsmen, censoring (more specifically right censoring) can be perceived in those situation of a match when a batsman remains not-out in limited overs cricket. Therefore, if any batsman remains not-out in a limited overs cricket then n_i be the number of batsmen survives minus the number of batsmen not-out in prior to b_i balls of a match. Now the Kaplan-Meier (KM) estimator in terms of the game of cricket is defined as

$S(b)={\displaystyle \prod _{b_i<b_{i+1}}^{}\left(1-\frac{O_i}{n_i}\right)}$  Where b₁  b₂  … and i = 1, 2, …, 120 (4)

Thus, the survival probabilities of the batsmen on the cricket pitch are computed using the above defined estimator. As we know that the precision of any estimate is reflected in the standard error of the estimate. Therefore, the standard error of KM estimate is computed as an essential aid to the interpretation of estimate. In this regard, Peto et. al. (1977) proposed a formula to compute standard error ofand it is defined as

$se\left\{\widehat{S}(b)\right\}=\frac{\widehat{S}(b)\sqrt{\left\{1-\widehat{S}(b)\right\}}}{\sqrt{n_i}}$      (5)

The expression (5) is conservative for standard error of because the standard errors will tend to be larger than they actually ought to be. Thus, the formula proposed by Greenwood’s (1926) for standard error of is usually recommended. The Greenwood’s (1926) standard error formula can be defined as

$se\left\{\widehat{S}(b)\right\}=\widehat{S}(b){\left\{{\displaystyle \sum _{}^{}\frac{O_i}{n_i\left(n_i-O_i\right)}}\right\}}^{\frac{1}{2}}$  For b_k≤b≤b_k+1          (6)

Now confidence interval for the corresponding value of the survival function can be obtained based on the above standard error of KM estimate. Finally, based on the KM estimate, a survival plot is being depicted to identify the survival ability of Indian and overseas batsmen on the cricket pitch.

Hypothesis testing

Hypothesis testing is the modest way of examining survival ability of overseas and Indian batsmen on the cricket pitch. It allows assessing the extent to which whether an observed set of data are consistent with a particular hypothesis or not. Here the working hypothesis is that there is no difference between the survival ability of overseas and Indian batsmen on the cricket pitch. The well-known log-rank test is used to test the working hypothesis. This is the appropriate non-parametric test to use when the right censored data are non-informative, as the case is comparable here in case of not-out batsmen. In order to apply log-rank test, the survival ability of overseas and Indian batsmen computed separately. It compares observed and expected number of event of interest from both the groups. The groups in log-rank test are labeled as overseas (coded as “1”) and Indian (coded as “2”) players. Now suppose there are k different distinct balls, b₁ < b₂ < … < b_k, where batsmen are out across the two groups. Let O_1i be the individual batsman out in overseas group and O_2i be batsman in Indian group. Again, suppose that n_1i be the total number batsmen out in overseas group and n_2i be the total number batsmen out in Indian group. Consequently, there are O_i = O_1i+O_2i batsmen out in a tournament from total of n_i = n_1i + n_2i batsmen, at b_i ball. Now, under the null hypothesis, it is defined as

$W_L=\frac{U_L^2}{V_L}~{\chi }_1^2$      (7)

Where $U_L={{\displaystyle \sum _{i=1}^k\left(O_{1i}-E_{1i}\right)}}^2$ and $V_L=Var\left(U_L\right)={\displaystyle \sum _{i=1}^k{v}_{1i}}$

Since the different balls are independent of one another, the term $V_L$ (i.e. variance of $U_L$ ) is sum of the variances of $O_{1i}$ and it is given by

$v_{1i}=\frac{n_{1i}{n}_{2i}{O}_i\left(n_i-O_i\right)}{n_i^2\left(n_i-1\right)}$      (8)

The statistics W_L summarizes the extent to which the observed number of survival balls in the two groups of batsmen deviate from those expected number of survival balls in the cricket pitch, under the null hypothesis of no group differences. The larger the value of log-rank test statistics (i.e. W_L), greater the evidence against the null hypothesis.

In IPL 2012, each franchisee has maximum of eight overseas players per squad. However, only four of them can be played in the playing XI for each match. There were 14 league matches usually played by each of the IPL team prior to knock-out stage of the tournament. Therefore, a lot of Indian as well as overseas players' performance (i.e. number of balls faced per match and out or not-out) can be collected from the scorecard of the matches. All this scorecard information is collected from the website www.espncricinfo.com from 2012 season of the IPL. A total of 1123 players are considered for the study, out of which 459 are overseas players and 664 are Indian players. The results of the analyses based on the methodology discussed above are provided below. From the above table, it has been observed that there are 103 and 162 cases are censored (i.e. not-out cases) corresponding to overseas and Indian players respectively. Overall 23.6% not-out case is being found for a total of 1123 cases (Table 1) (Table 2) (Table 3) (Table 4). 

From the above survival plot, one can easily be observed that there is a very little difference between standing ability of overseas and Indian batsmen on the pitch in IPL 2012. Up to 18 balls there is no difference between overseas and Indian batsmen. However, after 20 balls and up to 57 balls, it has been observed that overseas batsmen have moderately more standing ability on the cricket pitch than Indian players in IPL 2012. The following log-rank test has also confirmed that there is a significant difference in terms of standing ability on the cricket pitch between overseas and Indian batsmen (as p-value is 0.038 < 0.05) in IPL 2012. Earlier researcher such as Stefani and Clarke,⁸ Harville and Smith,⁹ Clarke and Norman,¹⁰ Clarke and Allsopp¹¹ and Allsopp and Clarke¹² have acknowledged that there is a significant home advantage for home team in the game of cricket. Now, both survival plot as well as log-rank test, have confirmed that there is a advantage for overseas batsmen than Indian batsmen. Thus, the advantage for Indian batsmen playing in their home country or home ground is become a question mark in IPL 2012. This finding can be considered as future scope of this research. May be there was no significant home advantage in IPL 2012 for the Indian batsmen (Figure 1).

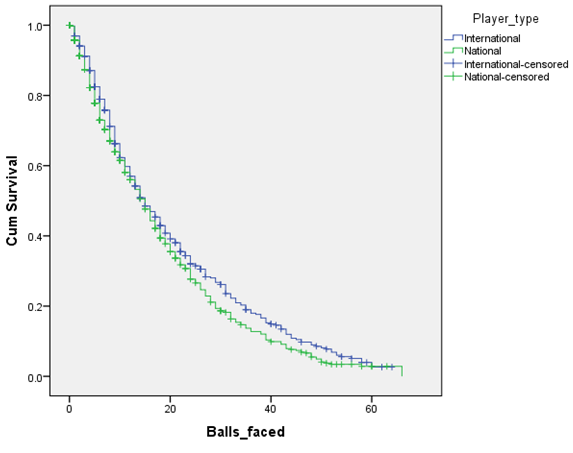
Figure 1 Survival functions of Indian and overseas batsmen in IPL 2014.

This study tries to examine the survival ability of Indian and overseas batsmen on the cricket pitch using survival analysis in Indian Premier League. The study has identified that overseas batsmen have moderately more standing ability on the cricket pitch than Indian batsmen after they faced 20 number of balls in IPL 2012. However, up to 20 number of balls, there is no difference between overseas and Indian batsmen in terms of standing ability on the cricket pitch. Since overseas batsmen have moderate advantage than Indian batsmen in IPL 2012; therefore, the home advantage for Indian players in IPL 2012 can be considered as future scope of the study. The proposed survival model can be used to forecast the survival rate of the batsmen in other format of cricket also, while the game is in progress. It can also be used to arrange the batting order of a team in the game of cricket based on the match situation.^13‒15

None.

Author declares that there is no conflict of interest.

1. Collett D. Modeling survival data in medical research, Second Edition. Chapman and Hall/CRC Press; 2003.
2. Danaher PJ. Estimating a cricketer’s batting average using the product limit estimator. The New Zealand Statistician. 1989;24:2‒5.
3. Cohen GL. Cricketing Chances: Mathematics and Computers in Sport. In: G Cohen, T Langtry, editors. Australia: Bond University, 2002. p. 1‒13.
4. Kimber AC, Hansford AR. A statistical analysis of batting in cricket. Journal of the Royal Statistical Society. 1993;156:443‒455.
5. Kaplan EL, Meier P. Nonparametric estimation from incomplete observations. Journal of the American Statistical Association. 1958;53:457‒481.
6. Das S. On generalized geometric distributions: Application to modelling scores in cricket and improved estimation of batting average in light of notout innings. Bangalore: Working paper series, Indian Institute of Management Bangalore; 2011.
7. Staden PJ, Meiring AT, Steyn JA, et al. Meaning batting averages in cricket. South African Statistical Journal Proceedings: Peer-reviewed Proceedings of the 52nd Annual Conference of the South African Statistical Association for 2010 (SASA 2010): Congress 1. 2010.
8. Stefani RT, Clarke SR. Predictions and home advantage for Australian rules football. Journal of Applied Statistics. 1992;19:251‒261.
9. Harville DA, Smith MH. The Home-Court Advantage: How Large is it and does it vary from Team to Team? The American Statistician. 1994;48:22‒28.
10. Clarke SR, Norman JM. Home Ground Advantage of Individual Clubs in English Soccer, Journal of the Royal Statistical Society (Series D: The Statistician). 1995;44:509‒521.
11. Clarke SR, Allsopp P. Fair Measures of Performance: The World Cup of Cricket. Journal of the Operational Research Society. 2001;52:471‒479.
12. Allsopp P, Clarke SR. Rating Teams and Analyzing Outcomes in One-day and Test cricket, Journal of the Royal Statistical Society. 2004;167:657‒667.
13. Greenwood M. The errors of sampling of the survival tables. London: Natural duration of cancer, A report of public health and statistical subjects. 1926.
14. Maini S, Narayanan S. The flaw in batting averages. The Acturay. 2007;30‒31.
15. Peto R, Pike MC, Armitage P, et al. Design and analysis of randomized clinical trials requiring prolonged observation of each patient. II. Analysis and examples. Brtish Journal of Cancer. 1977;35(1):1‒39.
16. Staden PJ. Comparison of cricketers' bowling and batting performances using graphical displays. Current Science. 2009;96(6):764‒766.